-
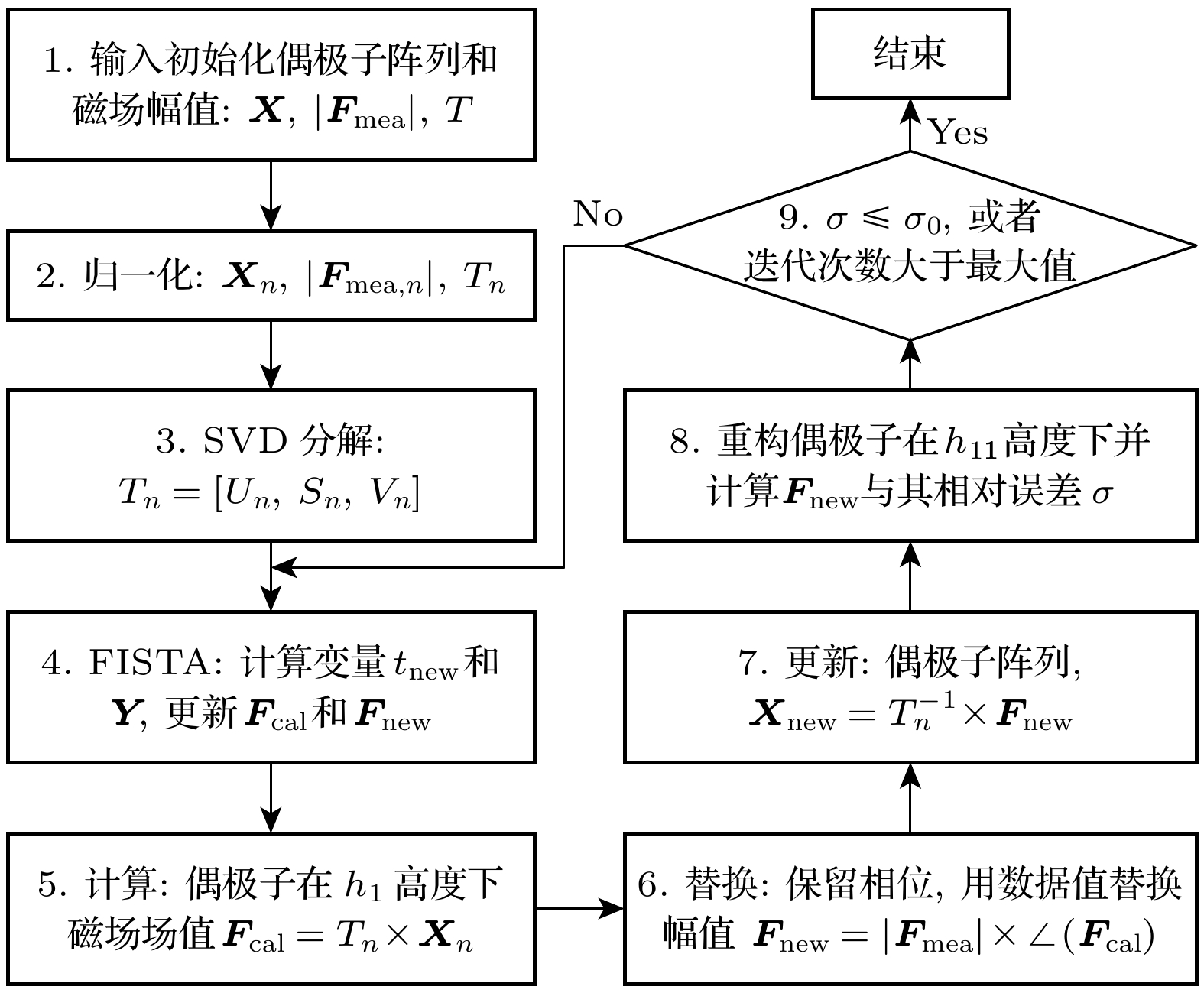
本文提出了一种基于奇异值分解(SVD)正则化和快速迭代收缩阈值算法(FISTA)的单层无相位辐射源重构算法. 该方法能够有效地识别集成电路中的电磁干扰源. 首先, 通过近场扫描获取电磁场数据, 随后利用源重构方法(SRM)在其表面重建等效偶极子模型. 引入SVD正则化项以提高算法的稳定性和抗噪声能力, FISTA技术则加速了算法的收敛速度. 为了验证该方法的准确性和对高斯噪声的鲁棒性, 进行了贴片天线仿真分析和芯片实验测试. 结果表明, 该算法在第35次迭代时达到稳定, 重构结果与仿真结果的相对误差为2.3%, 迭代时间仅为传统方法的61.7%, 相对误差减少了52%.
-
关键词:
- 奇异值分解 /
- 快速迭代收缩阈值算法 /
- 近场扫描 /
- 辐射源重构
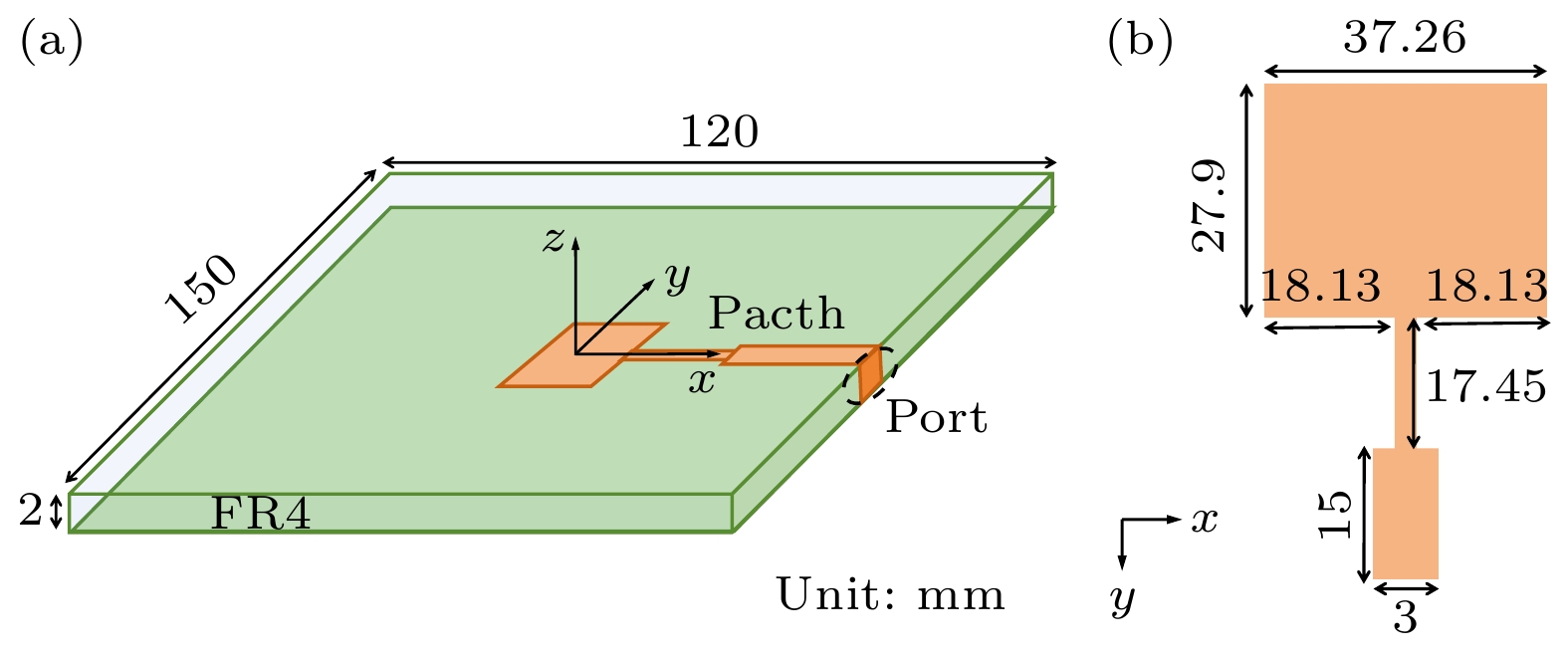
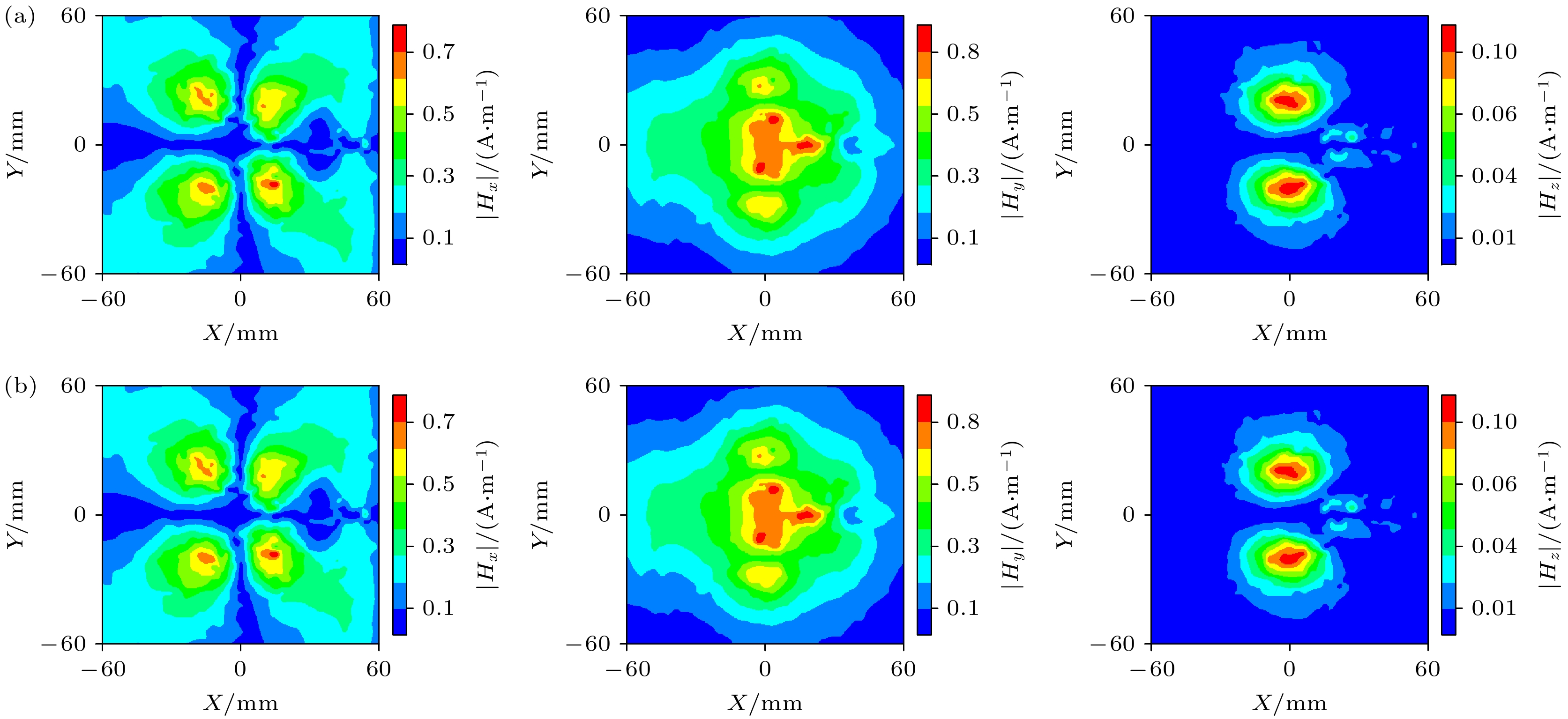
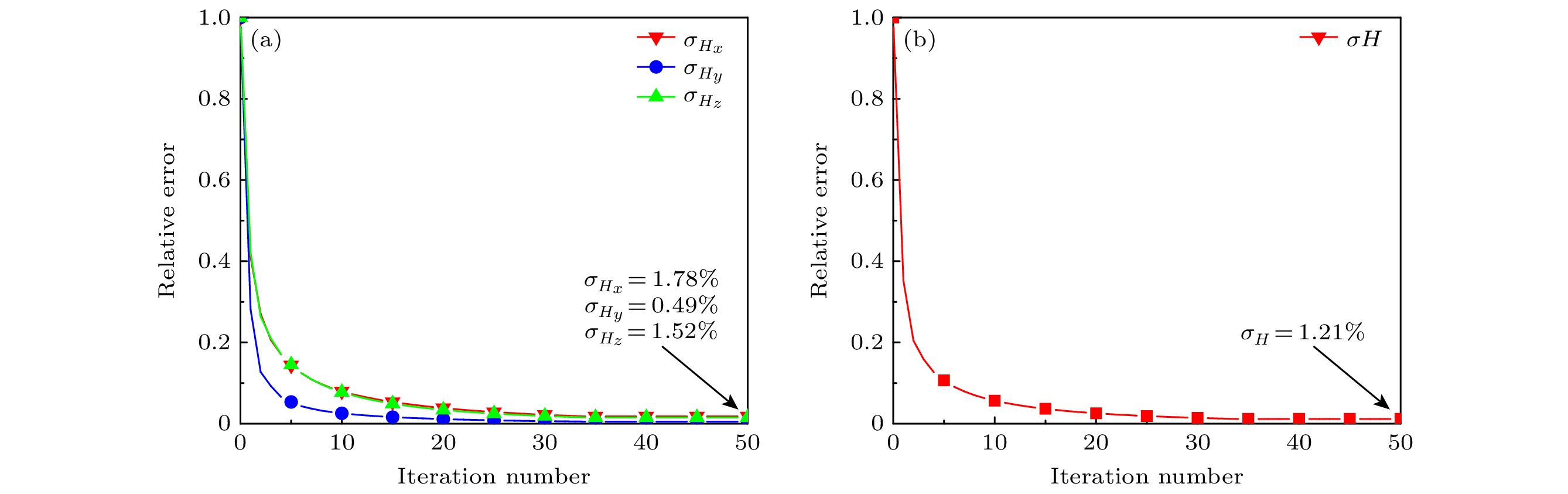
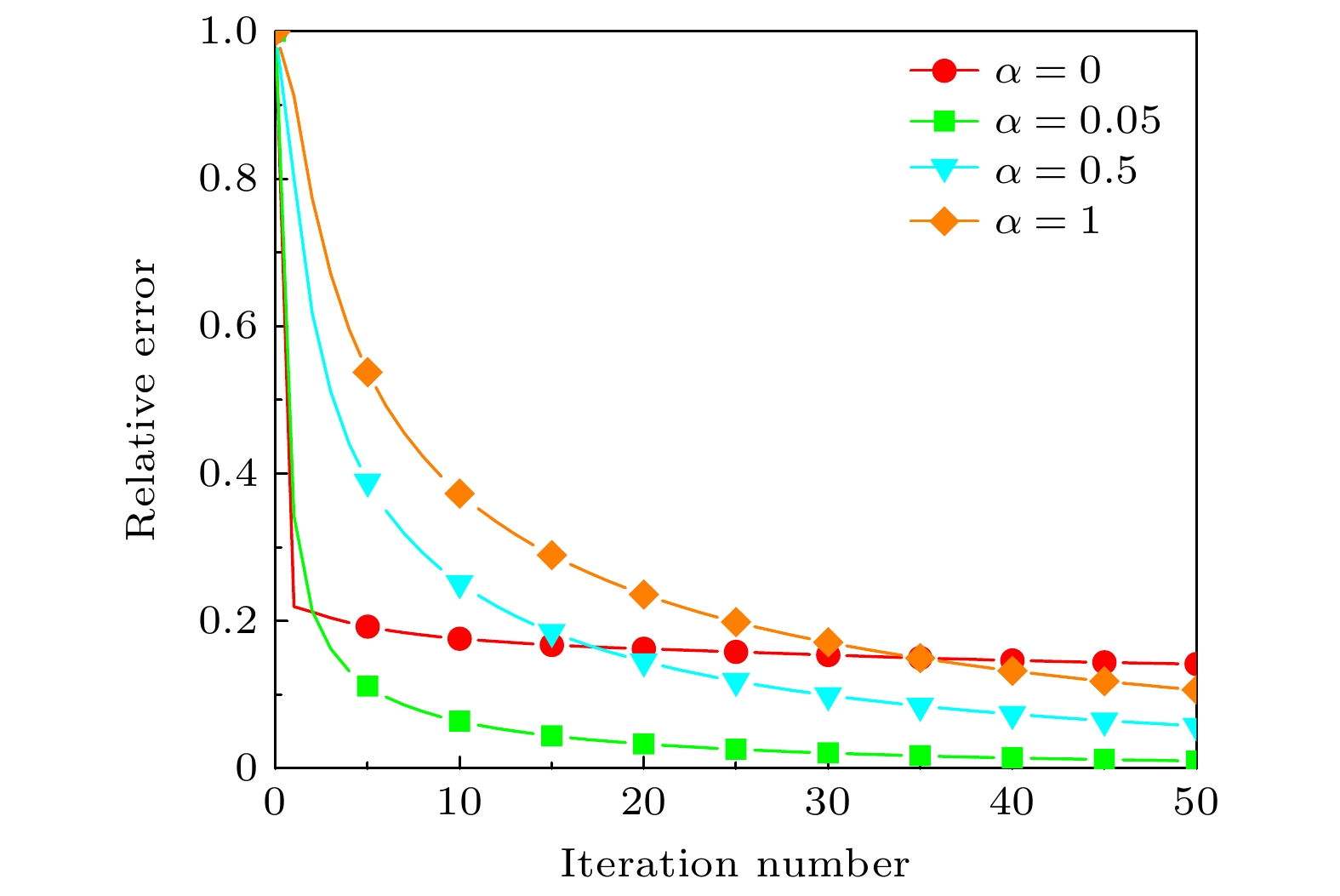
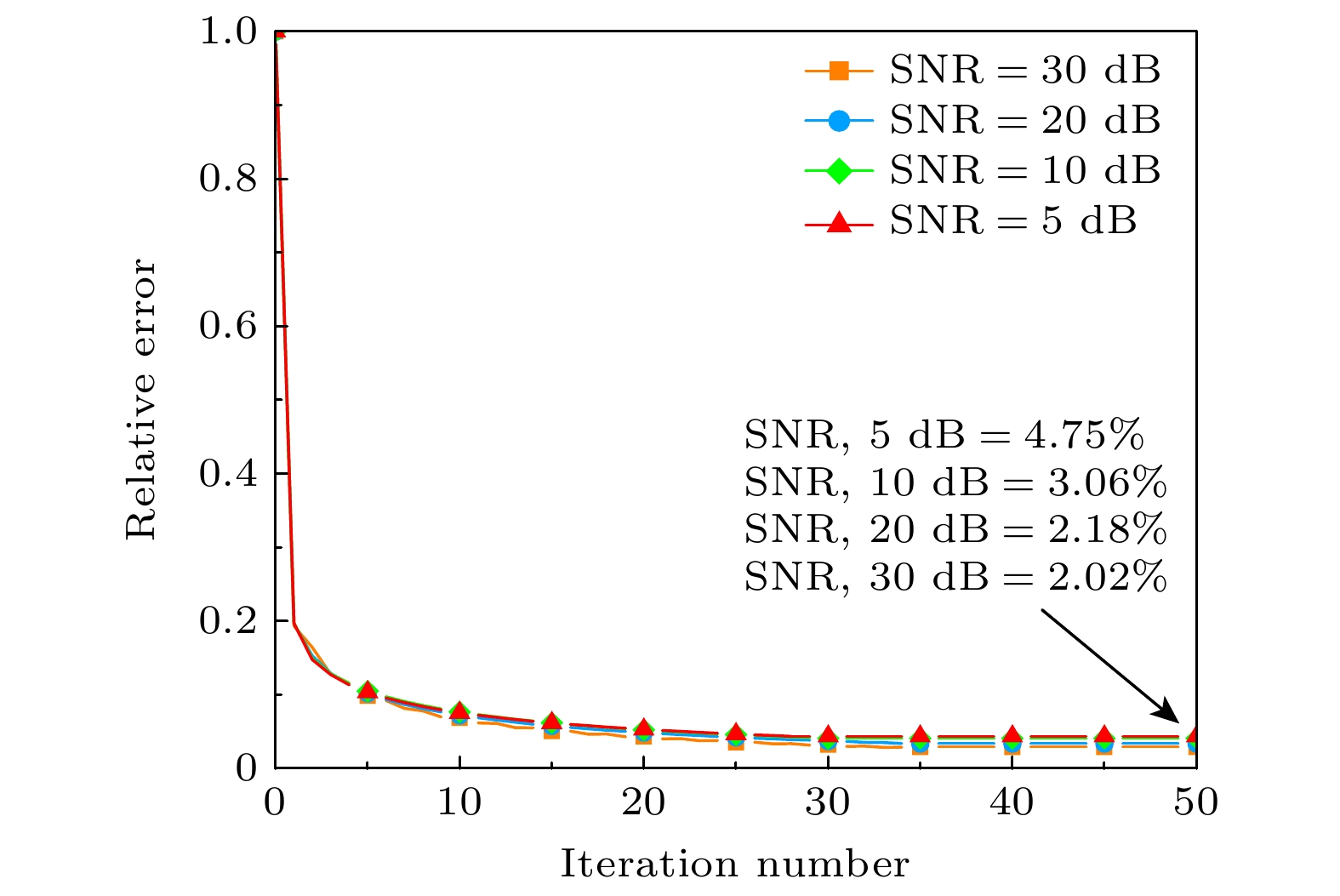
An algorithm of reconstructing phaseless radiation source based on singular value decomposition (SVD) regularization and fast iterative shrinkage-thresholding algorithm (FISTA) is proposed in this work, aiming at efficiently identifying electromagnetic interference (EMI) sources in integrated circuits (ICs). The method acquires electromagnetic field data through near-field scanning and reconstructs an equivalent dipole array on the surface of the radiation source by using the source reconstruction method (SRM). In the reconstruction process, the SVD regularization term enhances the algorithm's stability and noise resistance, while the FISTA accelerates the convergence speed. In order to validate the effectiveness of the proposed method, dipole array reconstruction is first performed using near-field data at a height of 5 mm for a patch antenna simulation model, followed by analyzing the magnetic field data at a 10 mm validation plane. At the 35th iteration, the total relative error of the reconstruction is 1.21%. The influence of the regularization parameter α on the result is then investigated, and it is found that when α = 0.05 the error is minimized. The method is also tested under different Gaussian white noise conditions, and the relative error is kept below 5%, which demonstrates strong robustness. Finally, the experiments on chips are conducted to verify the method. The proposed method converges stably within 35 iterations, with a relative error of 2.3% in the reconstruction results. The proposed method reduces the total iteration time to 61.7% of the single-layer phaseless interpolation algorithm, while achieving a 52% lower relative error than the double-layer phasless iteration algorithm. The experimental results show that the proposed method can reconstruct phaseless radiation source efficiently and accurately, and has good noise robustness, which is suitable for EMI analysis in ICs. -
Keywords:
- aingular value decomposition (SVD) /
- fast iterative shrinkage-thresholding algorithm (FISTA) /
- near-field scanning (NFS) /
- source reconstruction method (SRM)
[1] Schuman C D, Kulkarni S R, Parsa M, Mitchell J P, Date P, Kay B 2022 Nat. Comput. 2 10
 Google Scholar
Google Scholar
[2] Serpaud S, Boyer A, Dhia S B, Coccetti F 2022 IEEE Trans. Electromagn. Compat. 64 816
 Google Scholar
Google Scholar
[3] Boyer A, Nolhier N, Caignet F, Dhia S B 2022 IEEE Trans. Electromagn. Compat. 64 1230
 Google Scholar
Google Scholar
[4] 曹钟, 杜平安, 聂宝林, 任丹, 张其道 2014 63 124102
 Google Scholar
Google Scholar
Cao Z, Du P A, Nie B L, Ren D, Zhang Q D 2014 Acta. Phys. Sin. 63 124102
 Google Scholar
Google Scholar
[5] Yang R, Wei X C, Shu Y F, Yi D, Yang Y B 2019 IEEE Trans. Antennas Propag. 67 6821
 Google Scholar
Google Scholar
[6] Zhang J, Kam K W, Min J, Khilkevich V V, Pommerenke D, Fan J 2013 IEEE Trans Instrum. Meas. 62 648
 Google Scholar
Google Scholar
[7] Wang L, Zhang Y, Han F, Zhou J, Liu QH 2020 IEEE Trans. Microwave Theory Tech. 68 4151
 Google Scholar
Google Scholar
[8] Weng H, Beetner D G, DuBroff R E 2011 IEEE Trans. Electromagn. Compat. 53 891
 Google Scholar
Google Scholar
[9] Zuo P, Li Y, Xu Y, Zheng H, Li E P 2019 IEEE Trans. Compon. Packag. Manuf. Technol. 9 329
 Google Scholar
Google Scholar
[10] Yu Z, Mix J A, Sajuyigbe S, Slattery K P, Fan J 2012 IEEE Trans. Electromagn. Compat. 55 97
[11] Kornprobst J, Mauermayer R A M, Neitz O, Knapp J, Eibert T F 2019 Prog. Electromagn. Res. 165 47
 Google Scholar
Google Scholar
[12] Yi Z, Zou J, Tian X, Huang Q, Fang W, Shao W, En Y, Gao Y, Han P 2023 IEEE Trans. Electromagn. Compat. 65 879
 Google Scholar
Google Scholar
[13] Regue J R, Ribó M, Garrell J M, Martín A 2001 IEEE Trans. Electromagn. Compat 43 520
 Google Scholar
Google Scholar
[14] Han D H, Wei X C, Wang D, Liang W T, Song T H, Gao R X 2024 IEEE Trans. Electromagn. Compat. 66 566
 Google Scholar
Google Scholar
[15] Xiang F P, Li E P, Wei X C, Jin J M 2015 IEEE Trans. Electromagn. Compat. 57 1197
 Google Scholar
Google Scholar
[16] Shu Y F, Wei X C, Fan J, Yang R, Yang Y B 2019 IEEE Trans. Microwave Theory Tech. 67 1790
 Google Scholar
Google Scholar
[17] Zhang J, Fan J 2017 IEEE Trans. Electromagn. Compat. 59 557
 Google Scholar
Google Scholar
[18] Shu Y F, Wei X C, Yang R, Liu E X 2017 IEEE Trans. Electromagn. Compat. 60 937
[19] Yu Z W, Jason M, Sajuyigbe S, Slattery K P, Fan J 2013 IEEE Trans. Electromagn. Compat. 55 97
 Google Scholar
Google Scholar
[20] Beck A, Teboulle M 2009 SIAM J. Imaging Sci. 2 183
 Google Scholar
Google Scholar
-
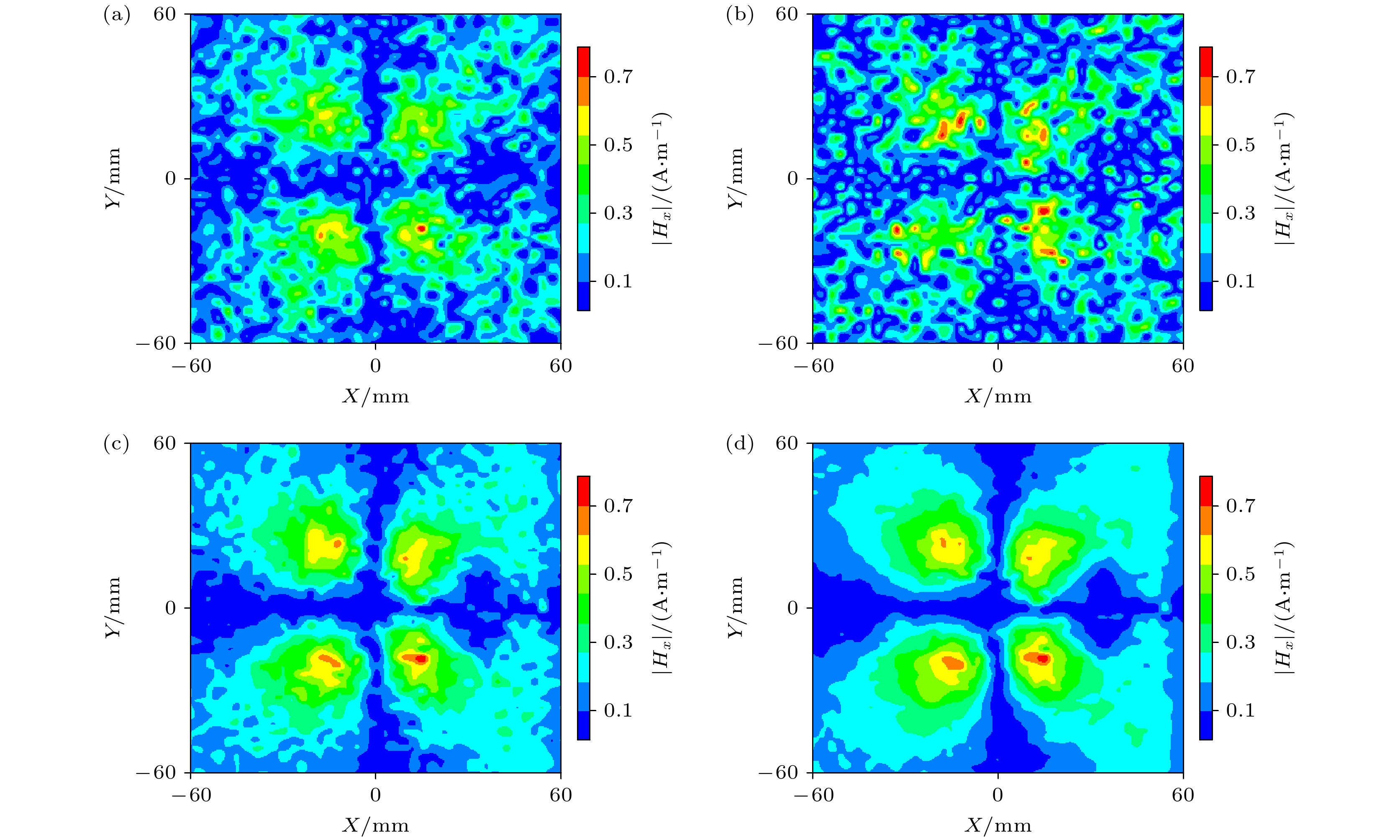
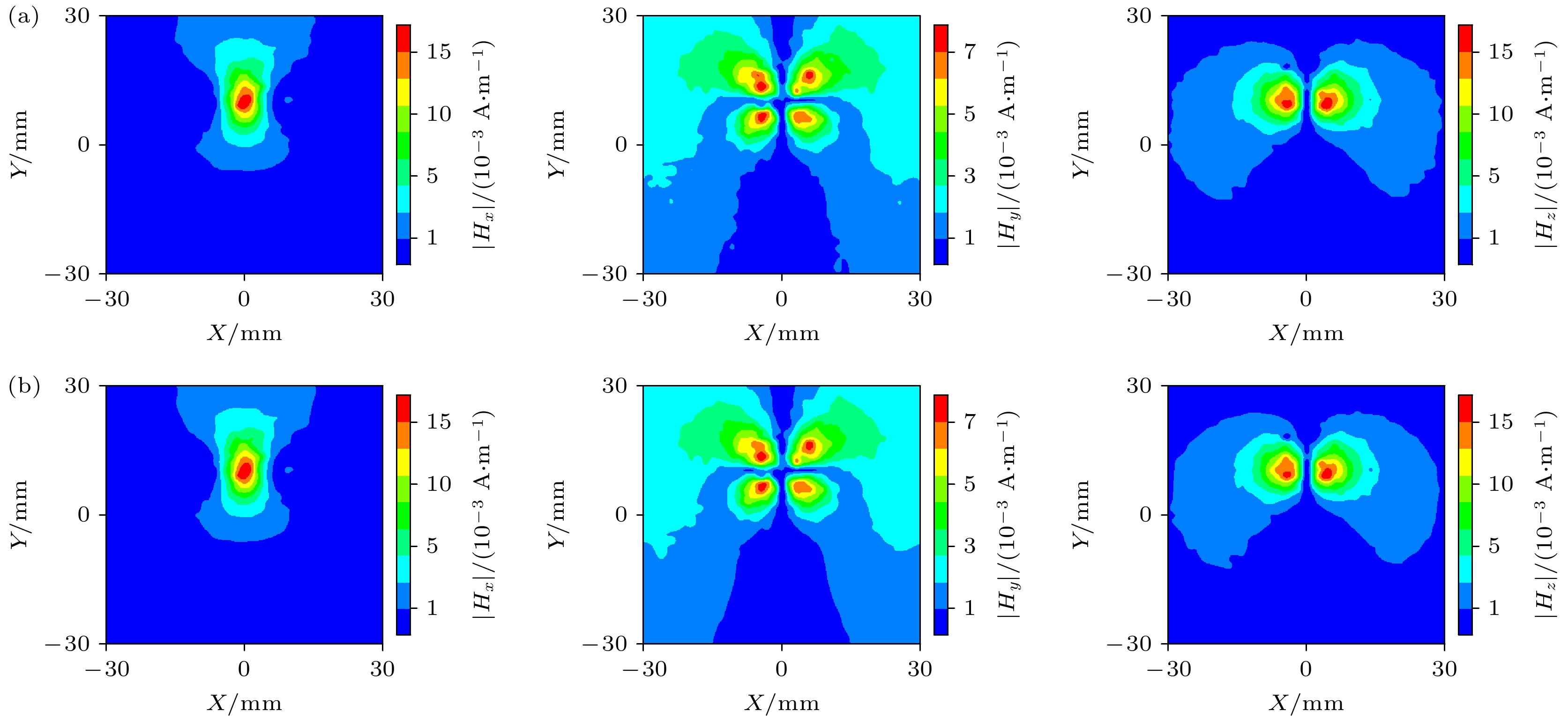
图 7 在不同水平的高斯白噪声下z = 12 mm, f = 2.5 GHz磁场|Hx|幅值 (a) SNR = 5 dB; (b) SNR = 10 dB; (c) SNR = 20 dB; (d) SNR = 30 dB
Fig. 7. Magnetic field $ \left|{H}_{x}\right| $ amplitude under different levels of white Gaussian noise, z = 12 mm, f = 2.5 GHz: (a) SNR = 5 dB; (b) SNR = 10 dB; (c) SNR = 20 dB; (d) SNR = 30 dB.
表 1 与现有方法的时间和相对误差进行对比
Table 1. Comparison of time and relative error with existing methods.
-
[1] Schuman C D, Kulkarni S R, Parsa M, Mitchell J P, Date P, Kay B 2022 Nat. Comput. 2 10
 Google Scholar
Google Scholar
[2] Serpaud S, Boyer A, Dhia S B, Coccetti F 2022 IEEE Trans. Electromagn. Compat. 64 816
 Google Scholar
Google Scholar
[3] Boyer A, Nolhier N, Caignet F, Dhia S B 2022 IEEE Trans. Electromagn. Compat. 64 1230
 Google Scholar
Google Scholar
[4] 曹钟, 杜平安, 聂宝林, 任丹, 张其道 2014 63 124102
 Google Scholar
Google Scholar
Cao Z, Du P A, Nie B L, Ren D, Zhang Q D 2014 Acta. Phys. Sin. 63 124102
 Google Scholar
Google Scholar
[5] Yang R, Wei X C, Shu Y F, Yi D, Yang Y B 2019 IEEE Trans. Antennas Propag. 67 6821
 Google Scholar
Google Scholar
[6] Zhang J, Kam K W, Min J, Khilkevich V V, Pommerenke D, Fan J 2013 IEEE Trans Instrum. Meas. 62 648
 Google Scholar
Google Scholar
[7] Wang L, Zhang Y, Han F, Zhou J, Liu QH 2020 IEEE Trans. Microwave Theory Tech. 68 4151
 Google Scholar
Google Scholar
[8] Weng H, Beetner D G, DuBroff R E 2011 IEEE Trans. Electromagn. Compat. 53 891
 Google Scholar
Google Scholar
[9] Zuo P, Li Y, Xu Y, Zheng H, Li E P 2019 IEEE Trans. Compon. Packag. Manuf. Technol. 9 329
 Google Scholar
Google Scholar
[10] Yu Z, Mix J A, Sajuyigbe S, Slattery K P, Fan J 2012 IEEE Trans. Electromagn. Compat. 55 97
[11] Kornprobst J, Mauermayer R A M, Neitz O, Knapp J, Eibert T F 2019 Prog. Electromagn. Res. 165 47
 Google Scholar
Google Scholar
[12] Yi Z, Zou J, Tian X, Huang Q, Fang W, Shao W, En Y, Gao Y, Han P 2023 IEEE Trans. Electromagn. Compat. 65 879
 Google Scholar
Google Scholar
[13] Regue J R, Ribó M, Garrell J M, Martín A 2001 IEEE Trans. Electromagn. Compat 43 520
 Google Scholar
Google Scholar
[14] Han D H, Wei X C, Wang D, Liang W T, Song T H, Gao R X 2024 IEEE Trans. Electromagn. Compat. 66 566
 Google Scholar
Google Scholar
[15] Xiang F P, Li E P, Wei X C, Jin J M 2015 IEEE Trans. Electromagn. Compat. 57 1197
 Google Scholar
Google Scholar
[16] Shu Y F, Wei X C, Fan J, Yang R, Yang Y B 2019 IEEE Trans. Microwave Theory Tech. 67 1790
 Google Scholar
Google Scholar
[17] Zhang J, Fan J 2017 IEEE Trans. Electromagn. Compat. 59 557
 Google Scholar
Google Scholar
[18] Shu Y F, Wei X C, Yang R, Liu E X 2017 IEEE Trans. Electromagn. Compat. 60 937
[19] Yu Z W, Jason M, Sajuyigbe S, Slattery K P, Fan J 2013 IEEE Trans. Electromagn. Compat. 55 97
 Google Scholar
Google Scholar
[20] Beck A, Teboulle M 2009 SIAM J. Imaging Sci. 2 183
 Google Scholar
Google Scholar
计量
- 文章访问数: 1206
- PDF下载量: 43
- 被引次数: 0













 下载:
下载: