-
传统磁力显微镜(MFM)的磁畴扫描是利用激光束反射探测探针和样品之间的静磁力. 因此, 对于MFM, 直接探测样品在交流磁场作用下的动态磁力仍然是一个挑战. 交变力磁力显微镜(A-MFM)使用Co-GdOx超顺磁探针可以实现在交流磁场(频率ωm)作用下探测动态磁力. 采集ωm和2ωm信号能准确地表示出样品的静态磁场(外加交流磁场对样品磁化状态没有影响)和动态磁场(外加交流磁场改变了样品磁化状态)的区域. 通过修改传统的tapping-lift扫描模式为一次tapping多次lift的扫描模式, A-MFM实现了三维空间的磁场探测. 本文证明了样品的静态和动态磁场随探针和样品之间距离z的变化, 满足Hz(z) = Hz(0)·exp(–kz). A-MFM可以研究材料的动态磁化过程, 也可以评价材料的磁均匀性(微观结构均匀性).In the scanning magnetic domain by using the conventional magnetic force microscopy (MFM), a laser beam reflection is used to detect the static magnetic force between probe and sample. Therefore, for the MFM, it is a challenge to directly detect the dynamic magnetic force between probe and sample under an external alternating-current (AC) magnetic field. In this study, it is proved that in an alternating magnetic force microscopy (A-MFM) a sensitive Co-GdOx superparamagnetic probe can be usedto detect the dynamic magnetic force under an external AC magnetic field (frequency ωm). In the present method, the magnetization of Co-GdOx probe is modulated by an external AC magnetic field. Collecting ωm and 2ωm signals by using the combination of phase-locked loop (PLL) and lock in amplifiers can accurately represent the static (DC, which stands for direct current) magnetic field areas (the external AC magnetic field has no effect on the magnetized status of the sample) and dynamic (AC) magnetic field areas (the external AC magnetic field changes the magnetized status of the sample) of an anisotropic Sr ferrite sintered magnet at the same time, respectively. The Sr ferrite sample is a single-domain-type magnet where magnetization mainly changes via magnetic rotation. The A-MFM method can measure the strength and identify the polarities of the static magnetic field of sample with a DC demagnetized state. By modifying the traditional tapping-lift mode into a tapping-multiply lift mode, the A-MFM by using superparamagnetic tips can measure the static and dynamic magnetic field distribution in three-dimensional (3D) space. It is proved that the static and dynamic magnetic field as a function of the distance z between probe and sample are both expressed as Hz(z) = Hz(0)·exp(–kz). The experimental data are consistent with the previous theoretical calculations. The A-MFM can be used to study the dynamic magnetization process and to evaluate the magnetic homogeneity (microstructural homogeneity) of magnetic materials.
-
Keywords:
- magnetic force microscopy /
- magnetic materials /
- dynamic magnetic force /
- superparamagnetic probe
[1] 李正华, 李翔 2014 63 178503
Google Scholar
Li Z H, Li X 2014 Acta Phys. Sin. 63 178503
Google Scholar
[2] Shinjo T, OKuno T, Hassdorf R, Shigeto K, Ono T 2000 Science 289 930
Google Scholar
[3] Schwarz A, Bode M, Wiesendanger R 2007 Scanning Probe Techniques: MFM and SP-MFM (New York: Wiley)
[4] Schwarz A, Wiesendanger R 2008 Nano Today 3 28
Google Scholar
[5] Koblischka M R, Hartmann U 2003 Ultramicroscopy 97 103
Google Scholar
[6] Liu L W, Dang H G, Sheng W, Wang Y, Cao J W, Bai J M, Wei F L 2013 Chin. Phys. B 22 047503
Google Scholar
[7] 薛慧, 马宗敏, 石云波, 唐军, 薛晨阳, 刘俊, 李艳君 2013 62 180704
Google Scholar
Xue H, Ma Z M, Shi Y B, Tang J, Xue C Y, Liu J, Li Y J 2013 Acta Phys. Sin. 62 180704
Google Scholar
[8] Jaafar M, Gomez-Herrero J, Gil A, Ares P, Vazquez M, Asenjo A 2009 Ultramicroscopy 109 693
Google Scholar
[9] Fang Y K, Zhu M G, Guo Y Q, Li W, Han B S 2004 Chin. Phys. Lett. 21 1655
Google Scholar
[10] Martin Y, Wickramasinghe H K 1987 Appl. Phys. Lett. 50 1455
Google Scholar
[11] Hartmann U 1999 Annu. Rev. Mater. Sci. 29 53
Google Scholar
[12] Nenadovic M, Strbac S, Rakocevic Z 2010 Appl. Surf. Sci. 256 1652
Google Scholar
[13] Obara G, Sakurai T, Ono O 2019 IEEE Trans. Magn. 55 6500504
[14] Rice P, Moreland J, Wadas A 1994 J. Appl. Phys. 75 6878
Google Scholar
[15] Liou S H, Yao Y D 1998 J. Magn. Magn. Mater. 190 130
Google Scholar
[16] Cao Y Z, Kumar P, Zhao Y, Yoshimura S, Saito H 2018 Appl. Phys. Lett. 112 223103
Google Scholar
[17] Cao Y Z, Nakayama S, Kumar P, Zhao Y, Kinoshita Y, Yoshimura S, Saito H 2018 Nanotechnology 29 305502
Google Scholar
[18] Lu W, Li Z H, Hatakeyama K, Egawa G, Yoshimura S, Saito H 2010 Appl. Phys. Lett. 96 143104
Google Scholar
[19] Li Z H, Hatakeyama K, Egawa G, Yoshimura S, Saito H 2012 Appl. Phys. Lett. 100 222405
Google Scholar
[20] Cao Y Z, Kumar P, Zhao Y, Suzuki Y, Yoshimura S, Saito H 2018 J. Magn. Magn. Mater. 462 119
Google Scholar
[21] Schwenk J, Marioni M, Romer S, Joshi N R, Hug H J 2014 Appl. Phys. Lett. 104 112412
Google Scholar
-
图 1 (a)静态和动态磁场测试的交变力磁力显微镜实验装置示意图; (b)探针扫描模式示意图, 首先轻敲获得一点的表面形貌, 之后探针多次抬举相同的高度测试磁力; 探针下落进行这一点样品表面的轻敲, 按照设置的步长移动到下一个点位置轻敲, 之后多次抬举测磁力, 这样循环测试; 这里, 设定抬举的次数为32, 每一次抬举的时间设置为60 ms, 每一次抬举位置的停留时间为 20 ms, 在抬举过程中探针的振动电压为轻敲时电压的20%
Fig. 1. (a) Schematic diagram of A-MFM with super paramagnetic tips for DC and AC magnetic fields measurement of magnetic materials. (b) Schematic diagram of sequential probe control. First measuring the topography (tapping), after tapping, tip was lifted by the same height between the adjacent lift points. The probe drops to tap the topography of the sample at this point, and moves to the next point according to the set step, and then lifts the probe several times, so that the cyclic test was carried out. The lift points number can be set, and the wait time of lift points can be set. In this experiment, the lift points were set as 32, the every lift procession was set as 60 ms, and the wait time was set as 20 ms. Using 20% of the tapping oscillation voltage of the supe rparamagnetic tips as a lift oscillation voltage.
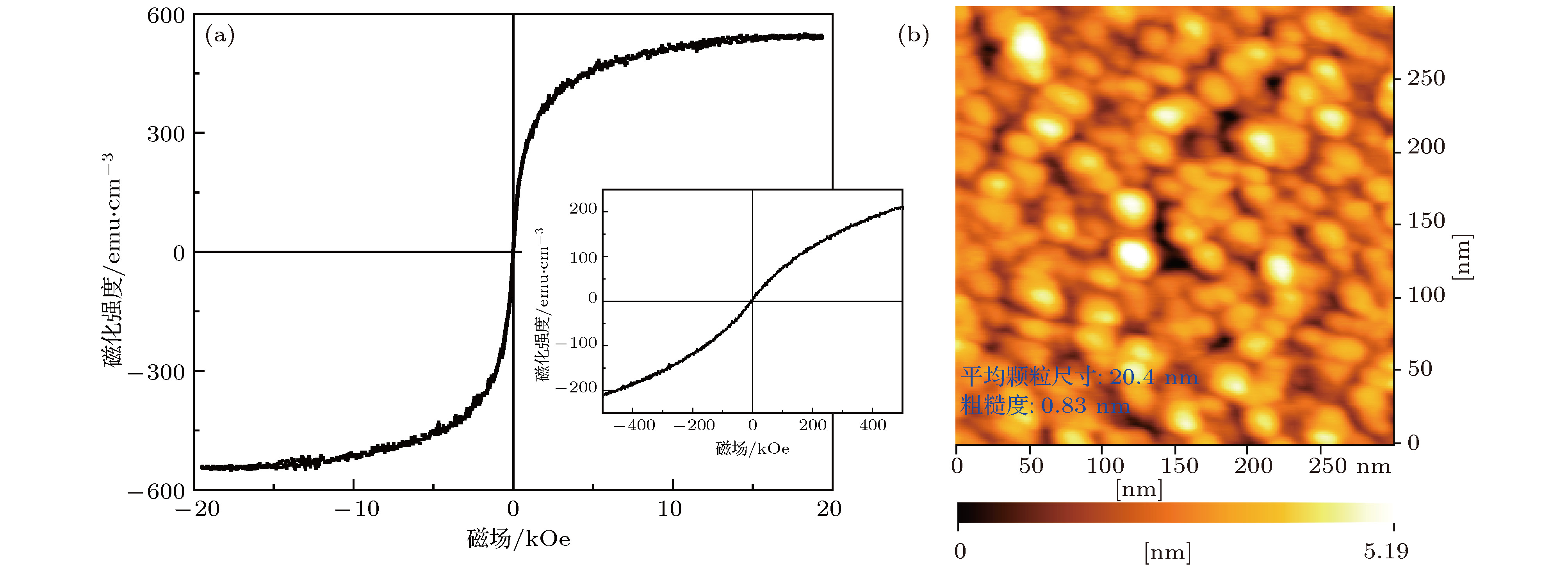
图 2 (a) 100 nm厚Co-GdOx薄膜在室温下20 kOe量程的面内磁滞回线, 插图为500 Oe量程的磁滞回线; (b)利用原子力显微镜使用Si探针测试100 nm厚Co-GdOx薄膜的表面形貌结果
Fig. 2. (a) In plane hysteresis loops of Co-GdOx films with 100 nm thickness at 300 K at the range 20 kOe, and the inset figure is the range of 500 Oe, (b) AFM topography image of Co-GdOx films with 100 nm thickness using Si probe.
图 3 一系列不同探针和样品距离(T-S)的Sr铁氧体的静态磁场的同相X图像(ωm信号) (a) 和动态磁场振幅R图像(2ωm信号) (c); (b)和(d)是图(a)和(c)在相同位置的线扫描, 这里T-S距离从574 nm到8794 nm
Fig. 3. A set of A-MFM in phase X images of ωm signal (a) and the A-MFM amplitude R images of 2ωm signal (c) of Sr ferrite sample at different distances between tip and sample (T-S) from 574 nm to 8794 nm; (b) and (d) are the line profiles of (a), (c) at the same positions, respectively.
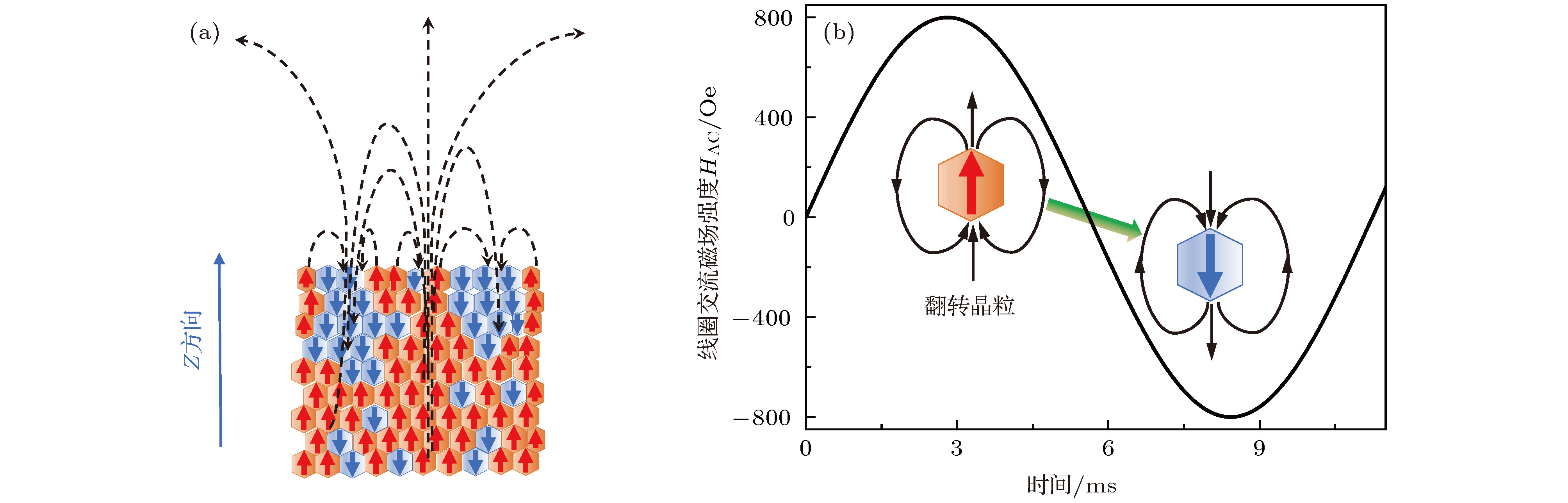
图 4 (a) Sr铁氧体的三维静态磁场分布示意图; (b)在线圈交流磁场作用下, Sr铁氧体矫顽力较小的晶粒的磁矩翻转示意图, 翻转的频率与线圈交流磁场频率相同, 这里线圈交流磁场频率是89 Hz, 振幅是800 Oe0-p(零点到峰值的强度)
Fig. 4. (a) Schematic of 3-D static (DC) magnetic field distribution of Sr ferrite sample; (b) the changed magnetized statement of the grain (a small coercivity) of Sr ferrite sample under an external AC magnetic field (frequency is 89 Hz, amplitude is 800 Oe (zero to peak intensity)).
图 5 图3(b)和图3(d)中位置1, 2和3的X图像静态磁场和R图像动态磁场的强度值随探针与样品之间的距离T-S变化曲线
Fig. 5. The plot of intensity values of A-MFM in phase X images of static (DC) magnetic field with ωm signal and A-MFM amplitude R images of dynamic (AC) magnetic field with 2ωm signal versus distance between super paramagnetic tip and Sr ferrite sample on the position 1, position 2 and position 3 in Fig.3(b), (d).
-
[1] 李正华, 李翔 2014 63 178503
Google Scholar
Li Z H, Li X 2014 Acta Phys. Sin. 63 178503
Google Scholar
[2] Shinjo T, OKuno T, Hassdorf R, Shigeto K, Ono T 2000 Science 289 930
Google Scholar
[3] Schwarz A, Bode M, Wiesendanger R 2007 Scanning Probe Techniques: MFM and SP-MFM (New York: Wiley)
[4] Schwarz A, Wiesendanger R 2008 Nano Today 3 28
Google Scholar
[5] Koblischka M R, Hartmann U 2003 Ultramicroscopy 97 103
Google Scholar
[6] Liu L W, Dang H G, Sheng W, Wang Y, Cao J W, Bai J M, Wei F L 2013 Chin. Phys. B 22 047503
Google Scholar
[7] 薛慧, 马宗敏, 石云波, 唐军, 薛晨阳, 刘俊, 李艳君 2013 62 180704
Google Scholar
Xue H, Ma Z M, Shi Y B, Tang J, Xue C Y, Liu J, Li Y J 2013 Acta Phys. Sin. 62 180704
Google Scholar
[8] Jaafar M, Gomez-Herrero J, Gil A, Ares P, Vazquez M, Asenjo A 2009 Ultramicroscopy 109 693
Google Scholar
[9] Fang Y K, Zhu M G, Guo Y Q, Li W, Han B S 2004 Chin. Phys. Lett. 21 1655
Google Scholar
[10] Martin Y, Wickramasinghe H K 1987 Appl. Phys. Lett. 50 1455
Google Scholar
[11] Hartmann U 1999 Annu. Rev. Mater. Sci. 29 53
Google Scholar
[12] Nenadovic M, Strbac S, Rakocevic Z 2010 Appl. Surf. Sci. 256 1652
Google Scholar
[13] Obara G, Sakurai T, Ono O 2019 IEEE Trans. Magn. 55 6500504
[14] Rice P, Moreland J, Wadas A 1994 J. Appl. Phys. 75 6878
Google Scholar
[15] Liou S H, Yao Y D 1998 J. Magn. Magn. Mater. 190 130
Google Scholar
[16] Cao Y Z, Kumar P, Zhao Y, Yoshimura S, Saito H 2018 Appl. Phys. Lett. 112 223103
Google Scholar
[17] Cao Y Z, Nakayama S, Kumar P, Zhao Y, Kinoshita Y, Yoshimura S, Saito H 2018 Nanotechnology 29 305502
Google Scholar
[18] Lu W, Li Z H, Hatakeyama K, Egawa G, Yoshimura S, Saito H 2010 Appl. Phys. Lett. 96 143104
Google Scholar
[19] Li Z H, Hatakeyama K, Egawa G, Yoshimura S, Saito H 2012 Appl. Phys. Lett. 100 222405
Google Scholar
[20] Cao Y Z, Kumar P, Zhao Y, Suzuki Y, Yoshimura S, Saito H 2018 J. Magn. Magn. Mater. 462 119
Google Scholar
[21] Schwenk J, Marioni M, Romer S, Joshi N R, Hug H J 2014 Appl. Phys. Lett. 104 112412
Google Scholar
下载:
计量
- 文章访问数: 9383
- PDF下载量: 104
- 被引次数: 0
