-
基于激子输运在聚合物给体/富勒烯(或非富勒烯)受体异质结太阳能电池光伏过程中的重要作用, 本文结合最新的实验进展, 从理论上提出了由非均匀场驱动的超快激子输运机制. 动力学模拟采用扩展的一维Su-Schrieffer-Heeger紧束缚模型结合非绝热的量子动力学方法, 而非均匀场主要考虑了由受限电荷诱导的非均匀电场和分子排列相关的非均匀构型场. 研究发现: 非均匀电场和构型场均可驱动激子实现超快输运, 其输运速度比由传统的Förster或Dexter机制主导的激子输运可分别提高1和2个数量级. 另外, 本文重点分析了这两种非均匀场对激子输运的驱动机制, 定量计算了它们各自诱导的驱动力. 最后, 针对影响这两种非均匀场分布的因素(包括受限电荷相对聚合物分子的距离和聚合物分子线性排列的斜率), 讨论了它们对激子输运动力学的影响.Due to the exciton migration dynamics playing an important role in the photovoltaic process of organic solar cells, which are usually composed of polymer donor and fullerene (or non-fullerene) acceptor, in this paper we propose a new strategy to achieve the ultrafast exciton migration in polymers. Here, the effects of some nonuniform fields on the exciton migration dynamics in polymers are emphasized, such as the nonuniform electric field and the nonuniform polymer packing configuration field. Both of the two kinds of nonuniform fields can be intrinsically existent or modulated in an actual photovoltaic system. In this work, the nonuniform electric field and the nonuniform configuration field are assumed to be separately created by a confined charge and a linear polymer packing, therefore, their model Hamiltonian is established. In dynamical simulations of the exciton migration dynamics in polymers, an extended version of one-dimensional Su-Schrieffer-Heeger tight-binding model combined with a nonadiabatic evolution method is employed. It is found that the nonuniform electric field and the nonuniform configuration field both can drive exciton to an ultrafast migration process. Compared with the exciton migration speed dominated by the traditional Förster or Dexter mechanism, the exciton migration speed dominated by the nonuniform electric field and that by the nonuniform configuration field can be increased by one and two orders of magnitude, respectively. In addition, the driving mechanisms of the two kinds of nonuniform fields for the exciton migration dynamics are separately clarified, where the corresponding driving forces are also quantitatively calculated. Finally, in view of the factors affecting the distributions of the two kinds of nonuniform fields (such as the distance d between confined charge and polymer, and the linear packing slope k between polymers), we discuss their effects on the exciton migration dynamics. It is found that the exciton migration in polymer can be apparently accelerated by shortening the distance d between confined charge and polymer, and there exists a critical value of d, beyond which the exciton will be dissociated into free charges in its migration process. For the linear packing slope k between polymers, we find that there exists an optimal value, at which the exciton has the highest migration speed in polymers.
-
Keywords:
- polymers /
- photovoltaic effect /
- exciton migration
[1] Ameri T, Khoram P, Min J, Brabec C J 2013 Adv. Mater. 25 4245
Google Scholar
[2] An Q S, Zhang F J, Zhang J, Tang W H, Deng Z B, Hu B 2016 Energy Environ. Sci. 9 281
Google Scholar
[3] 於黄忠 2013 62 027201
Google Scholar
Yu H Z 2013 Acta Phys. Sin. 62 027201
Google Scholar
[4] Yuan J, Zhang Y Q, Zhou L Y, Zhang G C, Yip H L, Lau T K, Lu X H, Zhu C, Peng H J, Johnson P A, Leclerc M, Cao Y, Ulanski J, Li Y F, Zou Y P 2019 Joule 3 1
Google Scholar
[5] Meng L X, Zhang Y M, Wan X J, Li C X, Zhang X, Wang Y B, Ke X, Xiao Z, Ding L M, Xia R X, Yip H L, Cao Y, Chen Y S 2018 Science 361 1094
Google Scholar
[6] Janssen R A J, Nelson J 2013 Adv. Mater. 25 1847
Google Scholar
[7] Cheng P, Zhan X W 2016 Chem. Soc. Rev. 45 2544
Google Scholar
[8] Bjorgaard J A, Köse M E 2015 RSC Adv. 5 8432
Google Scholar
[9] Scholes G D, Rumbles G 2006 Nat. Mater. 5 683
Google Scholar
[10] 王文静, 孟瑞璇, 李元, 高琨 2014 63 197901
Google Scholar
Wang W J, Meng R X, Li Y, Gao K 2014 Acta Phys. Sin. 63 197901
Google Scholar
[11] Ruini A, Caldas M J, Bussi G, Molinari E 2002 Phys. Rev. Lett. 88 206403
Google Scholar
[12] Gao K, Liu X J, Liu D S, Xie S J 2008 Phys. Lett. A 372 2490
Google Scholar
[13] Kaake L G, Moses D, Heeger A J 2015 Phys. Rev. B 91 075436
Google Scholar
[14] Heeger A J 2014 Adv. Mater. 26 10
Google Scholar
[15] Dimitrov S, Schroeder B, Nielsen C, Bronstein H, Fei Z, McCulloch I, Heeney M, Durrant J 2016 Polymers 8 14
Google Scholar
[16] Förster T 1948 Ann. Phys. 2 55
[17] Dexter D L 1953 J. Chem. Phys. 21 836
Google Scholar
[18] Menke S M, Holmes R J 2014 Energy Environ. Sci. 7 499
Google Scholar
[19] Mikhnenko O V, Blom P W M, Nguyen T Q 2015 Energy Environ. Sci. 8 1867
Google Scholar
[20] Scarongella M, de Jonghe-Risse J, Buchaca-Domingo E, Causa M, Fei Z, Heeney M, Moser J E, Stingelin N, Banerji N 2015 J. Am. Chem. Soc. 137 2908
Google Scholar
[21] Kaake L G, Jasieniak J J, Bakus R C, Welch G C, Moses D, Bazan G C, Heeger A J 2012 J. Am. Chem. Soc. 134 19828
Google Scholar
[22] Kaake L G, Moses D, Heeger A J 2013 J. Phys. Chem. Lett. 4 2264
Google Scholar
[23] Kaake L G, Zhong C, Love J A, Nagao I, Bazan G C, Nguyen T Q, Huang F, Cao Y, Moses D, Heeger A J 2014 J. Phys. Chem. Lett. 5 2000
Google Scholar
[24] Smith S L, Chin A W 2015 Phys. Rev. B 91 201302
Google Scholar
[25] Najafov H, Lee B, Zhou Q, Feldman L C, Podzorov V 2010 Nat. Mater. 9 938
Google Scholar
[26] Jin X U, Price M B, Finnegan J R, Boott C E, Richter J M, Rao A, Menke S M, Friend R H, Whittell G R, Manners I 2018 Science 360 897
Google Scholar
[27] Su W P, Schrieffer J, Heeger A J 1979 Phys. Rev. Lett. 42 1698
Google Scholar
[28] Heeger A J, Kivelson S, Schrieffer J, Su W P 1988 Rev. Mod. Phys. 60 781
Google Scholar
[29] Hu D, Yu J, Wong K, Bagchi B, Rossky P J, Barbara P E 2000 Nature 405 1030
Google Scholar
[30] Yao H, Qian D, Zhang H, Qin Y, Xu B, Cui Y, Yu R, Gao F, Hou J H 2018 Chin. J. Chem 36 491
Google Scholar
[31] Yuan Y, Reece T J, Sharma P, Poddar S, Ducharme S, Gruverman A, Yang Y, Huang J S 2011 Nat. Mater. 10 296
Google Scholar
[32] Karak S, Page Z A, Tinkham J S, Lahti P M, Emrick T, Duzhko V V 2015 Appl. Phys. Lett. 106 103303
Google Scholar
[33] Meng R X, Li Y, Gao K, Qin W, Wang L X 2017 J. Phys. Chem. C 121 20546
Google Scholar
[34] 赵二海, 孙鑫, 陈科, 付柔励 2000 49 1778
Google Scholar
Zhao E H, Sun X, Chen K, Fu R L 2000 Acta Phys. Sin. 49 1778
Google Scholar
[35] Sun X, Fu R L, Yonemitsu K, Nasu K 2000 Phys. Rev. Lett. 84 2830
Google Scholar
[36] McMahon D P, Cheung D L, Troisi A 2011 J. Phys. Chem. Lett. 2 2737
Google Scholar
[37] McEniry E J, Wang Y, Dundas D, Todorov T N, Stella L, Miranda R P, Fisher A J, Horsfield A P, Race C P, Mason D R, Foulkes W M C, Sutton A P 2010 Eur. Phys. J. B 77 305
Google Scholar
-
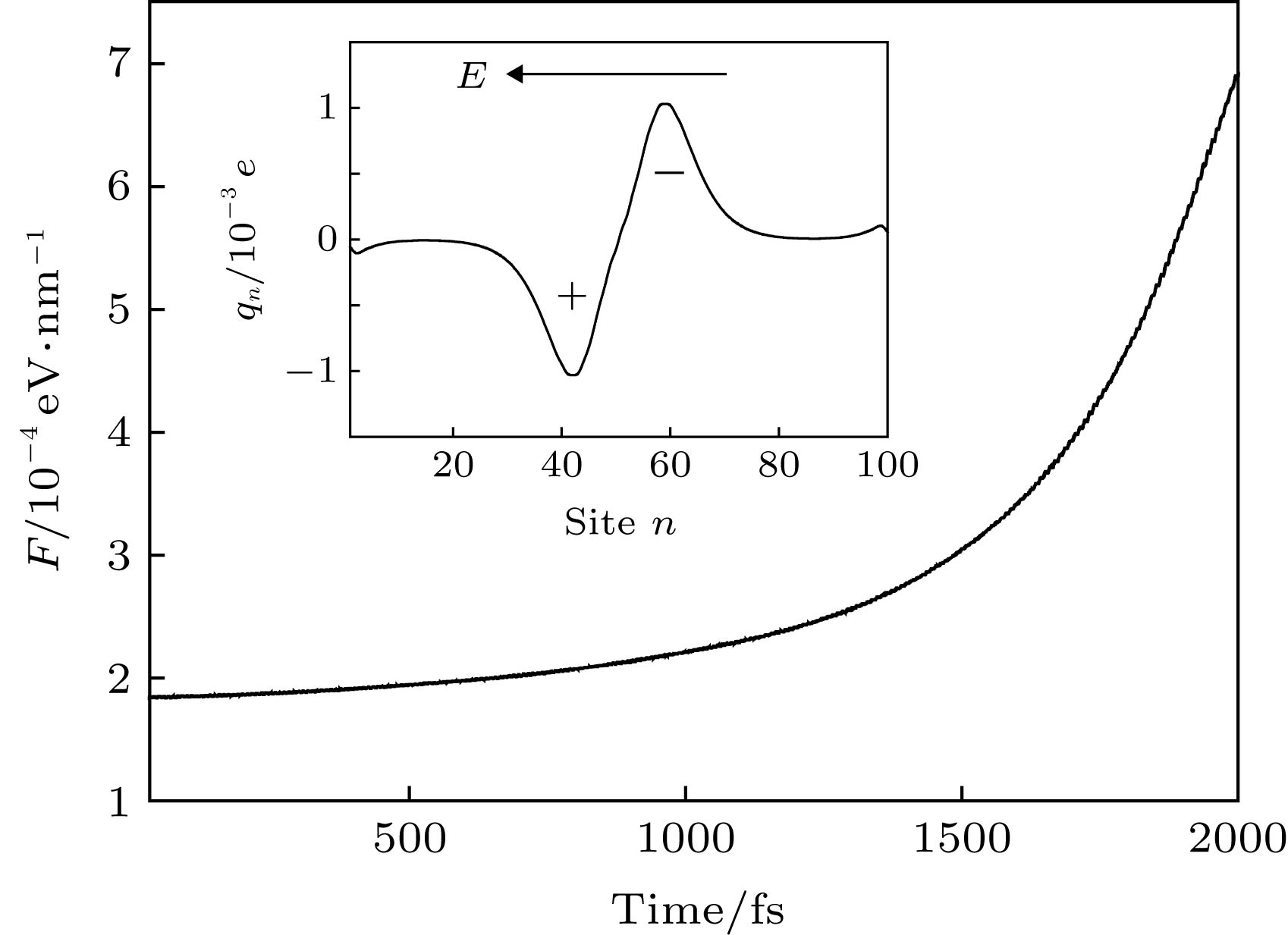
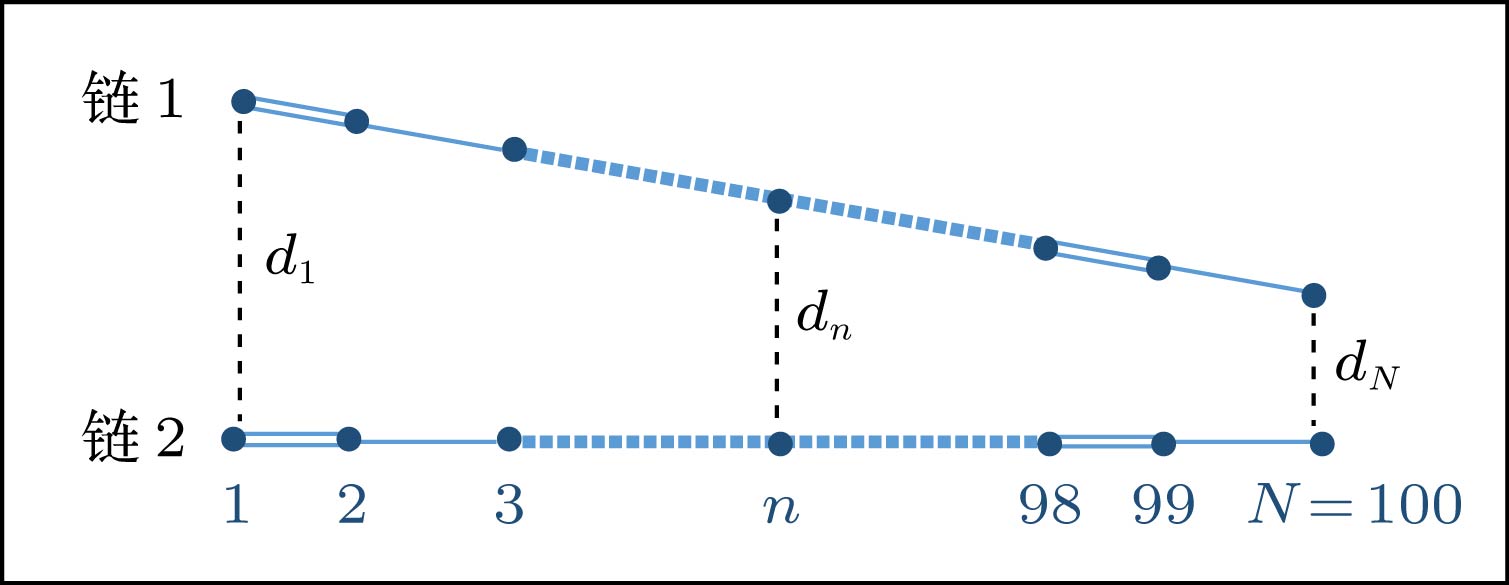
图 1 受限正电荷 (电荷量为
$\left| e \right|$ )相对于聚合物链的位置, d为电荷与链右端点的距离; 曲线为d = 3 nm时电场强度沿分子链的分布, 负号表示电场的方向与分子链的正方向相反Fig. 1. Schematic diagram about the position of a confined charge (q =
$\left| e \right|$ ) relative to the polymer chain, d shows the distance between the charge and the right chain-end; the curve describes the distribution of the induced electric field E along the polymer chain with the case of d = 3 nm, where the minus sign means that the direction of the electric field is opposite to that of the chain.
图 2 激子在非均匀电场(d = 3 nm)驱动下沿聚合物链超快输运对应的晶格动力学演化, 其初始产生时的中心位置为nc = 30
Fig. 2. Time evolution about the lattice configuration of an exciton in a polymer chain driven by a nonuniform electric field with d = 3 nm, where the exciton is initially generated at a central position of nc = 30.
图 3 非均匀电场诱导激子输运的驱动力F随时间的变化; 插图为t = 1000 fs时激子内极化的正电荷与负电荷的分布
Fig. 3. Variation of the driving force F as a function of the time. The inset presents the polarized positive charges and negative charges in the exciton at the time t = 1000 fs.
图 4 不同非均匀电场(通过改变d调控)驱动下激子中心位置nc随时间的演化
Fig. 4. Time evolution of the exciton center nc along the polymer chain driven by different nonuniform electric fields, which can be modulated by changing the value of d.
图 5 线性排列构型的耦合双分子链, dn为分子链垂直最近邻格点间的距离
Fig. 5. Schematic diagram of two coupled polymer chains with a linear interchain packing configuration, where dn indicates the distance between the vertical-neighbor sites.
图 6 激子在线性链间构型场 (k = 0.03)驱动下在分子间扩展及沿分子链输运的晶格动力学演化, 激子初始产生在第1条分子链上, 中心位置为nc = 30
Fig. 6. Time evolution about the lattice configuration of an exciton in two coupled polymer chains driven by the nonuniform configuration field with a linear coefficient k = 0.03.
图 7 线性构型场(k = 0.03)诱导的激子驱动力F沿分子链的分布, 插图为激子产生能
$\Delta E$ 随链间距离dn的变化Fig. 7. Distribution of the driving force F along polymer chains driven by a linear configuration with k = 0.03. The inset presents the dependence of the exciton creation energy
$\Delta E$ upon the interchain distance dn.
图 8 不同线性分子排列构型场(通过改变k调控)下激子中心位置nc随时间的演化
Fig. 8. Time evolution of the exciton center nc along polymer chains driven by different configuration fields, which can be modulated by changing the value of k.
-
[1] Ameri T, Khoram P, Min J, Brabec C J 2013 Adv. Mater. 25 4245
Google Scholar
[2] An Q S, Zhang F J, Zhang J, Tang W H, Deng Z B, Hu B 2016 Energy Environ. Sci. 9 281
Google Scholar
[3] 於黄忠 2013 62 027201
Google Scholar
Yu H Z 2013 Acta Phys. Sin. 62 027201
Google Scholar
[4] Yuan J, Zhang Y Q, Zhou L Y, Zhang G C, Yip H L, Lau T K, Lu X H, Zhu C, Peng H J, Johnson P A, Leclerc M, Cao Y, Ulanski J, Li Y F, Zou Y P 2019 Joule 3 1
Google Scholar
[5] Meng L X, Zhang Y M, Wan X J, Li C X, Zhang X, Wang Y B, Ke X, Xiao Z, Ding L M, Xia R X, Yip H L, Cao Y, Chen Y S 2018 Science 361 1094
Google Scholar
[6] Janssen R A J, Nelson J 2013 Adv. Mater. 25 1847
Google Scholar
[7] Cheng P, Zhan X W 2016 Chem. Soc. Rev. 45 2544
Google Scholar
[8] Bjorgaard J A, Köse M E 2015 RSC Adv. 5 8432
Google Scholar
[9] Scholes G D, Rumbles G 2006 Nat. Mater. 5 683
Google Scholar
[10] 王文静, 孟瑞璇, 李元, 高琨 2014 63 197901
Google Scholar
Wang W J, Meng R X, Li Y, Gao K 2014 Acta Phys. Sin. 63 197901
Google Scholar
[11] Ruini A, Caldas M J, Bussi G, Molinari E 2002 Phys. Rev. Lett. 88 206403
Google Scholar
[12] Gao K, Liu X J, Liu D S, Xie S J 2008 Phys. Lett. A 372 2490
Google Scholar
[13] Kaake L G, Moses D, Heeger A J 2015 Phys. Rev. B 91 075436
Google Scholar
[14] Heeger A J 2014 Adv. Mater. 26 10
Google Scholar
[15] Dimitrov S, Schroeder B, Nielsen C, Bronstein H, Fei Z, McCulloch I, Heeney M, Durrant J 2016 Polymers 8 14
Google Scholar
[16] Förster T 1948 Ann. Phys. 2 55
[17] Dexter D L 1953 J. Chem. Phys. 21 836
Google Scholar
[18] Menke S M, Holmes R J 2014 Energy Environ. Sci. 7 499
Google Scholar
[19] Mikhnenko O V, Blom P W M, Nguyen T Q 2015 Energy Environ. Sci. 8 1867
Google Scholar
[20] Scarongella M, de Jonghe-Risse J, Buchaca-Domingo E, Causa M, Fei Z, Heeney M, Moser J E, Stingelin N, Banerji N 2015 J. Am. Chem. Soc. 137 2908
Google Scholar
[21] Kaake L G, Jasieniak J J, Bakus R C, Welch G C, Moses D, Bazan G C, Heeger A J 2012 J. Am. Chem. Soc. 134 19828
Google Scholar
[22] Kaake L G, Moses D, Heeger A J 2013 J. Phys. Chem. Lett. 4 2264
Google Scholar
[23] Kaake L G, Zhong C, Love J A, Nagao I, Bazan G C, Nguyen T Q, Huang F, Cao Y, Moses D, Heeger A J 2014 J. Phys. Chem. Lett. 5 2000
Google Scholar
[24] Smith S L, Chin A W 2015 Phys. Rev. B 91 201302
Google Scholar
[25] Najafov H, Lee B, Zhou Q, Feldman L C, Podzorov V 2010 Nat. Mater. 9 938
Google Scholar
[26] Jin X U, Price M B, Finnegan J R, Boott C E, Richter J M, Rao A, Menke S M, Friend R H, Whittell G R, Manners I 2018 Science 360 897
Google Scholar
[27] Su W P, Schrieffer J, Heeger A J 1979 Phys. Rev. Lett. 42 1698
Google Scholar
[28] Heeger A J, Kivelson S, Schrieffer J, Su W P 1988 Rev. Mod. Phys. 60 781
Google Scholar
[29] Hu D, Yu J, Wong K, Bagchi B, Rossky P J, Barbara P E 2000 Nature 405 1030
Google Scholar
[30] Yao H, Qian D, Zhang H, Qin Y, Xu B, Cui Y, Yu R, Gao F, Hou J H 2018 Chin. J. Chem 36 491
Google Scholar
[31] Yuan Y, Reece T J, Sharma P, Poddar S, Ducharme S, Gruverman A, Yang Y, Huang J S 2011 Nat. Mater. 10 296
Google Scholar
[32] Karak S, Page Z A, Tinkham J S, Lahti P M, Emrick T, Duzhko V V 2015 Appl. Phys. Lett. 106 103303
Google Scholar
[33] Meng R X, Li Y, Gao K, Qin W, Wang L X 2017 J. Phys. Chem. C 121 20546
Google Scholar
[34] 赵二海, 孙鑫, 陈科, 付柔励 2000 49 1778
Google Scholar
Zhao E H, Sun X, Chen K, Fu R L 2000 Acta Phys. Sin. 49 1778
Google Scholar
[35] Sun X, Fu R L, Yonemitsu K, Nasu K 2000 Phys. Rev. Lett. 84 2830
Google Scholar
[36] McMahon D P, Cheung D L, Troisi A 2011 J. Phys. Chem. Lett. 2 2737
Google Scholar
[37] McEniry E J, Wang Y, Dundas D, Todorov T N, Stella L, Miranda R P, Fisher A J, Horsfield A P, Race C P, Mason D R, Foulkes W M C, Sutton A P 2010 Eur. Phys. J. B 77 305
Google Scholar
下载:
计量
- 文章访问数: 8218
- PDF下载量: 59
- 被引次数: 0
