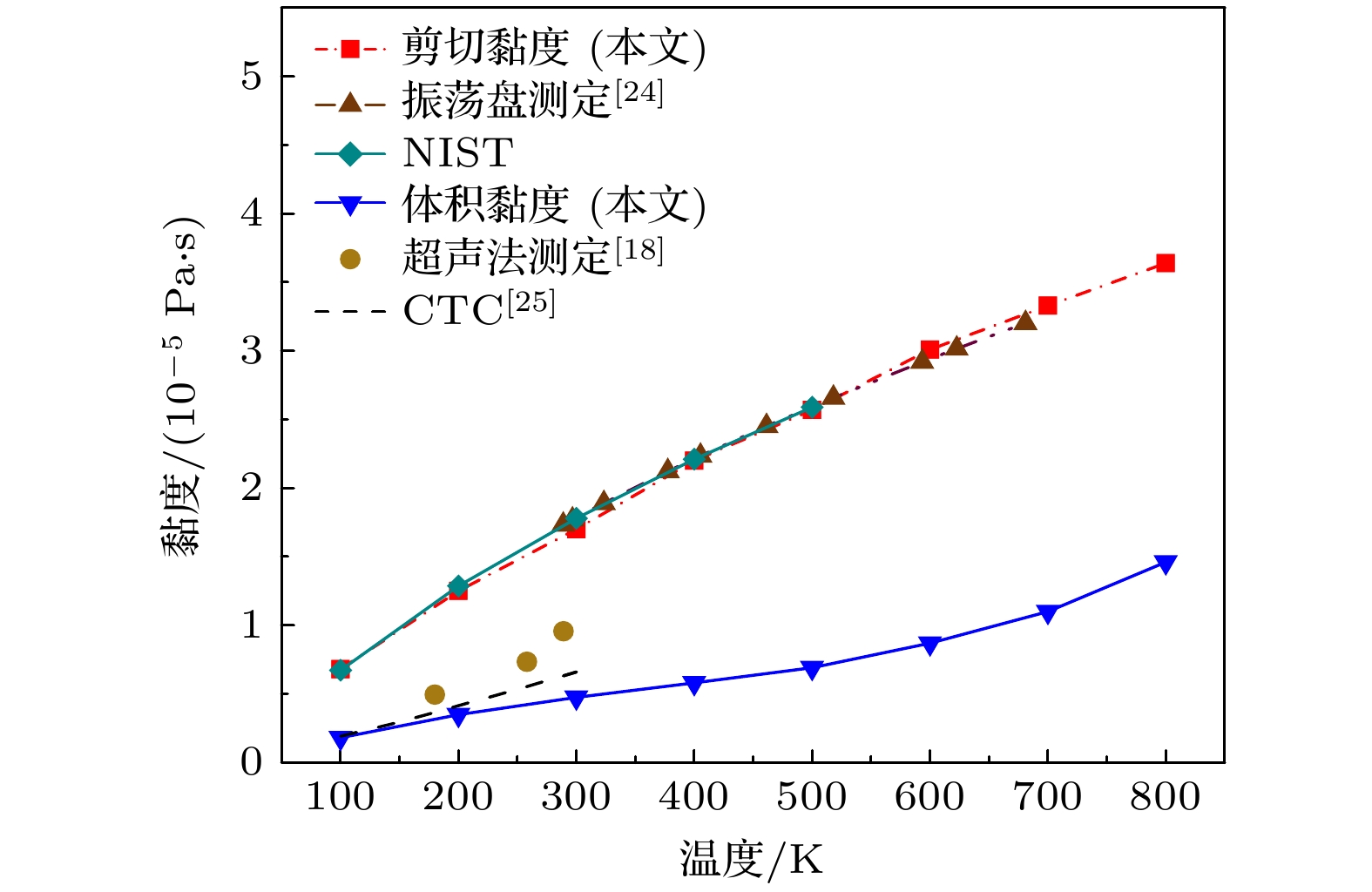
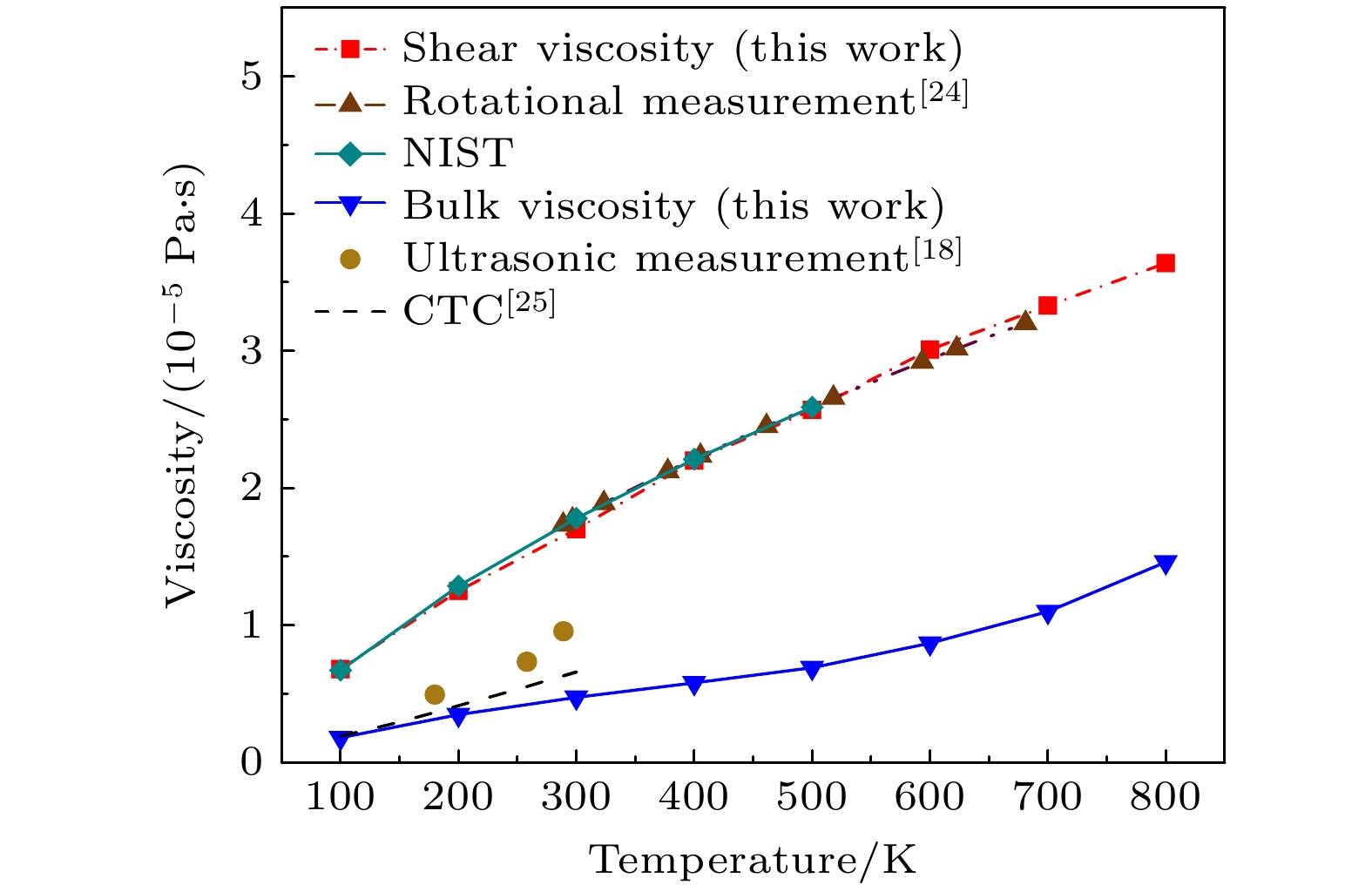
-
本文结合密度泛函理论与平衡分子动力学模拟, 构建了从量子力学到连续介质力学的跨尺度耦合模型, 基于所建立的高精度势函数与Green-Kubo线性响应理论, 研究了极性分子CO气体在100—800 K温度范围内的剪切黏度与体积黏度. 分子动力学模拟基于C语言编程实现, 采用自适应时间步长算法以提高计算效率. 研究结果表明, CO的体积黏度结果对势函数敏感性明显高于剪切黏度, 不同传统方法因相应原因高估了体积黏度; 所得体积黏度随温度的变化相对于剪切黏度具有显著的非线性规律; 模型采用低体系压力与大体系规模可有效减小统计涨落幅度, 提高体积黏度计算的收敛性与可靠性. 本研究阐释了CO气体黏度的微观动力学机制, 同时可为高温非平衡流动(如高超声速边界层、等离子体输运等)黏度机理研究提供理论参考.Viscosity is an essential transport property in gas dynamics, especially the bulk viscosity, which exhibits more complex behavior. Carbon monoxide (CO) is a molecule of weak polarity, which exists in many important fields such as combustion and coke metallurgy. In order to effectively uncover the mechanism of the CO viscosity, this study dealt with it from a microscopic view. A transcale model is built which integrates density functional theory (DFT, first-principles) calculations with equilibrium molecular dynamics (EMD) simulations to establish a microscale foundation. Based on that, a fitted high-precision potential function is formed, then by using the Green-Kubo linear response theory, the shear and bulk viscosities of CO are achieved in a medium temperature range of 100–800 K. The MD simulation is implemented with C programming language, and an adaptive time-step algorithm is applied so that the computational efficiency is significantly enhanced. The resulting bulk viscosity exhibits quite obvious sensitivity to the potential function of the molecule system, while the shear viscosity shows little. Unlike the shear viscosity, which appears more linear, the bulk viscosity shows clear nonlinear behavior that changes with temperature. Correspondingly, traditional theoretic models and experimental results from different literature indicate that the bulk viscosity at medium temperatures is overestimated to various degrees. Fitting functions on the shear and bulk viscosities in the defined temperature range are established, respectively. Additionally, the lower system pressure and larger system size in the model effectively reduce statistical pressure fluctuations and improve the convergence of relevant laws. This work elucidates the microscopic mechanism of CO viscosity and provides a high-fidelity theoretical tool for modeling the viscosity of high-temperature nonequilibrium gas flows (e.g. hypersonic boundary layers, and plasma transport).
-
Keywords:
- density functional theory /
- potential function /
- molecular dynamics /
- shear viscosity /
- bulk viscosity /
- nonlinearity
[1] 李志辉, 梁杰, 李中华, 李海燕, 吴俊林, 戴金雯, 唐志共 2018 空气动力学学报 36 826
Google Scholar
Li Z H, Liang J, Li Z H, Li H Y, Wu J L, Dai J W, Tang Z G 2018 Acta Aerodyn. Sin. 36 826
Google Scholar
[2] 罗仕超, 张志刚, 柳军, 龚红明, 胡守超, 吴里银, 常雨, 庄宇, 李贤, 黄成扬 2023 力学学报 55 2439
Google Scholar
Luo S C, Zhang Z G, Liu J, Gong H M, Hu S C, Wu L Y, Chang Y, Zhuang N, Li X, Huang C Y 2023 Chin. J. Theor. Appl. Mech. 55 2439
Google Scholar
[3] 邢赫威, 陈占秀, 杨历, 苏瑶, 李源华, 呼和仓 2024 73 094701
Google Scholar
Xing H W, Chen Z X, Yang L, Su Y, Li Y H, Huhe C 2024 Acta Phys. Sin. 73 094701
Google Scholar
[4] Qian X S 1946 J. Math. Phys. 25 247
Google Scholar
[5] 樊菁 2013 力学进展 43 185
Google Scholar
Fan J 2013 Adv. Mech. 43 185
Google Scholar
[6] Bruno D, Frezzotti A, Ghiroldi G P 2015 Phys. Fluids 27 057101
Google Scholar
[7] Tokumasu T, Matsumoto Y 2000 JSME Int J. Ser. B 43 288
Google Scholar
[8] 李锦, 耿湘人, 陈坚强, 江定武 2016 应用数学和力学 37 1403
Google Scholar
Li J, Geng X R, Chen J J, Jiang D W 2016 Appl. Math. Mech. 37 1403
Google Scholar
[9] Valentini P, Zhang C, Schwartzentruber T E 2012 Phys. Fluids 24 106101
Google Scholar
[10] Baidakov V, Protsenko S, Kozlova Z 2012 J. Chem. Phys. 137 164507
Google Scholar
[11] Baidakov V G, Protsenko S P 2014 J. Chem. Phys. 141 114503
Google Scholar
[12] Sharma B, Kumar R 2019 AIP Conf. Proc. 2132 090003
Google Scholar
[13] Parker J G, Adams C E, Stavseth R M 1953 J. Acoust. Soc. Am. 25 263
Google Scholar
[14] Marcy S J 1990 AIAA J. 28 171
Google Scholar
[15] Dukhin A S, Goetz P J 2009 J. Chem. Phys. 130 124519
Google Scholar
[16] Gu Z, Ubachs W 2013 Opt. Lett. 38 1110
Google Scholar
[17] Carnevale E H, Carey C, Larson G 1967 J. Chem. Phys. 47 2829
Google Scholar
[18] 赵宁波, 郑洪涛, 李淑英 2018 哈尔滨工程大学学报 39 60
Google Scholar
Zhao N B, Zheng H T, Li S Y 2018 J. Harbin Eng. Univ. 39 60
Google Scholar
[19] Kubo R 1985 Pure Appl. Chem. 57 201
Google Scholar
[20] Hellmann R 2013 Mol. Phys. 111 387
Google Scholar
[21] Cramer M S 2012 Phys. Fluids 24 066102
Google Scholar
[22] Lu T, Chen F 2013 J. Mol. Model 19 5387
Google Scholar
[23] Kasper P K 2017 J. Phys. Chem. A 121 9092
Google Scholar
[24] Abbaspour M, Goharshadi E K 2006 Chem. Phys. 330 313
Google Scholar
[25] Hong Q Z, Bartolomei M, Coletti C, Lombardi A, Sun Q H, Pirani F 2021 Molecules 26 7152
Google Scholar
[26] Vogel E 2012 Int. J. Thermophys 33 741
Google Scholar
[27] Heck E L, Dickinson A S 1995 Physica A 217 107
Google Scholar
-
图 1 CO分子体系示意图(灰球、红色球分别代表C, O原子)
Fig. 1. Schematic diagram of the CO molecular system (the gray and red spheres represent C and O atoms, respectively).
图 2 CO-CO不同构型下的势能变化 (a) I1, I2与I3型; (b) A1, A2与A3型; (c) Z1, Z2与Z3型; (d) T1与T2型; (e) H1, H2与X型
Fig. 2. Potential energy of CO-CO under different configurations: (a) Types I1, I2, and I3; (b) types A1, A2, and A3; (c) types Z1, Z2, and Z3; (d) types T1 and T2; (e) types H1, H2, and X.
图 3 CO分子的初始分布 (a)初始分子质心位置; (b)初始速率分布
Fig. 3. Initial distribution of CO molecules: (a) Initial positions of molecular centers of mass; (b) initial velocity distribution.
图 4 不同温度系统下CO的剪切黏度与体积黏度
Fig. 4. Shear viscosity and bulk viscosity of CO in systems at different temperatures.
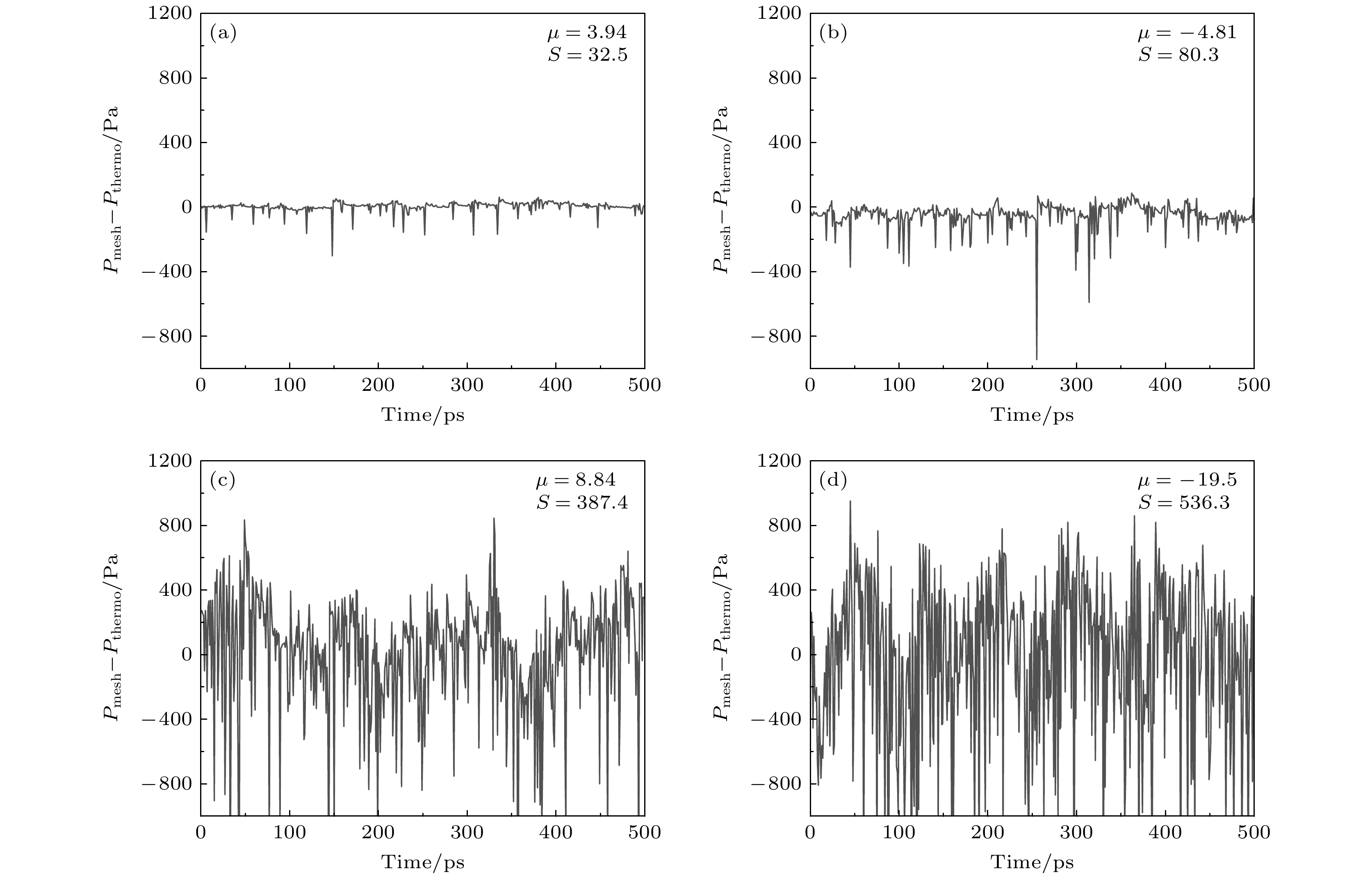
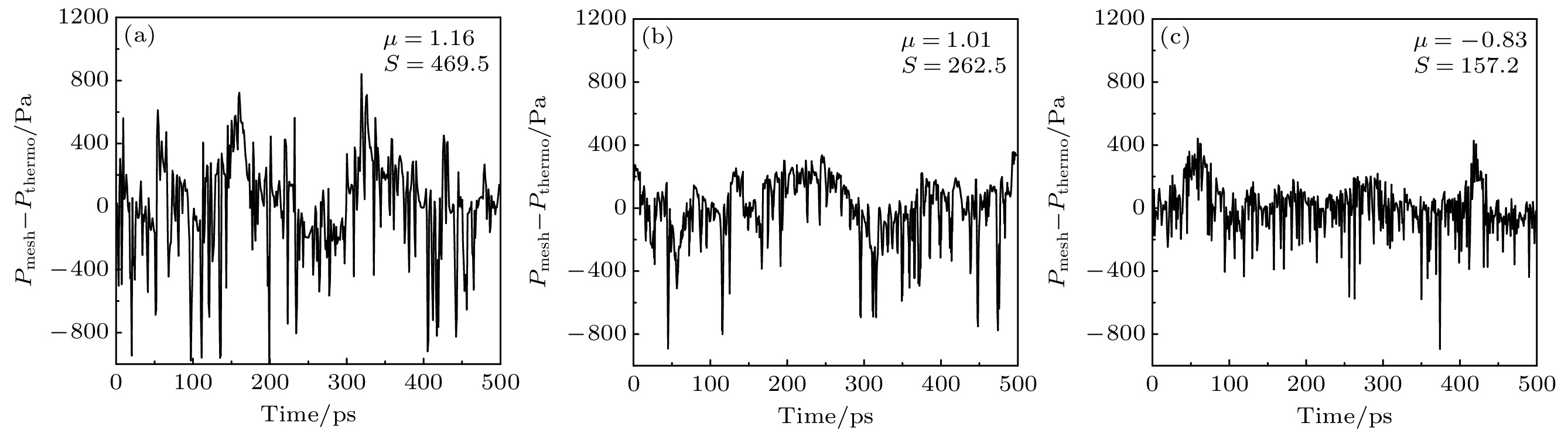
图 5 不同压力下系统平衡后$ {P_{{\text{mech}}}} - {P_{{\text{thermo}}}} $随模拟时间的变化(图中分别给出了其均值μ与标准差S) (a) p = 0.25 atm; (b) p = 0.5 atm; (c) p = 1.5 atm; (d) p = 2 atm
Fig. 5. Variation of $ {P_{{\text{mech}}}} - {P_{{\text{thermo}}}} $ with time after equilibration in systems under different pressures, with the mean value and the standard deviation presented, respectively: (a) p = 0.25 atm; (b) p = 0.5 atm; (c) p = 1.5 atm; (d) p = 2 atm.
图 6 分子数不同的体系平衡后$ {P_{{\text{mech}}}} - {P_{{\text{thermo}}}} $随运行时间的变化(图中分别给出了其均值μ与标准差S) (a) N = 500; (b) N = 1000; (c) N = 1500
Fig. 6. Variation of $ {P_{{\text{mech}}}} - {P_{{\text{thermo}}}} $ with time after equilibration in systems with different numbers of molecules, with the mean value and the standard deviation presented, respectively: (a) N = 500; (b) N = 1000; (c) N = 1500.
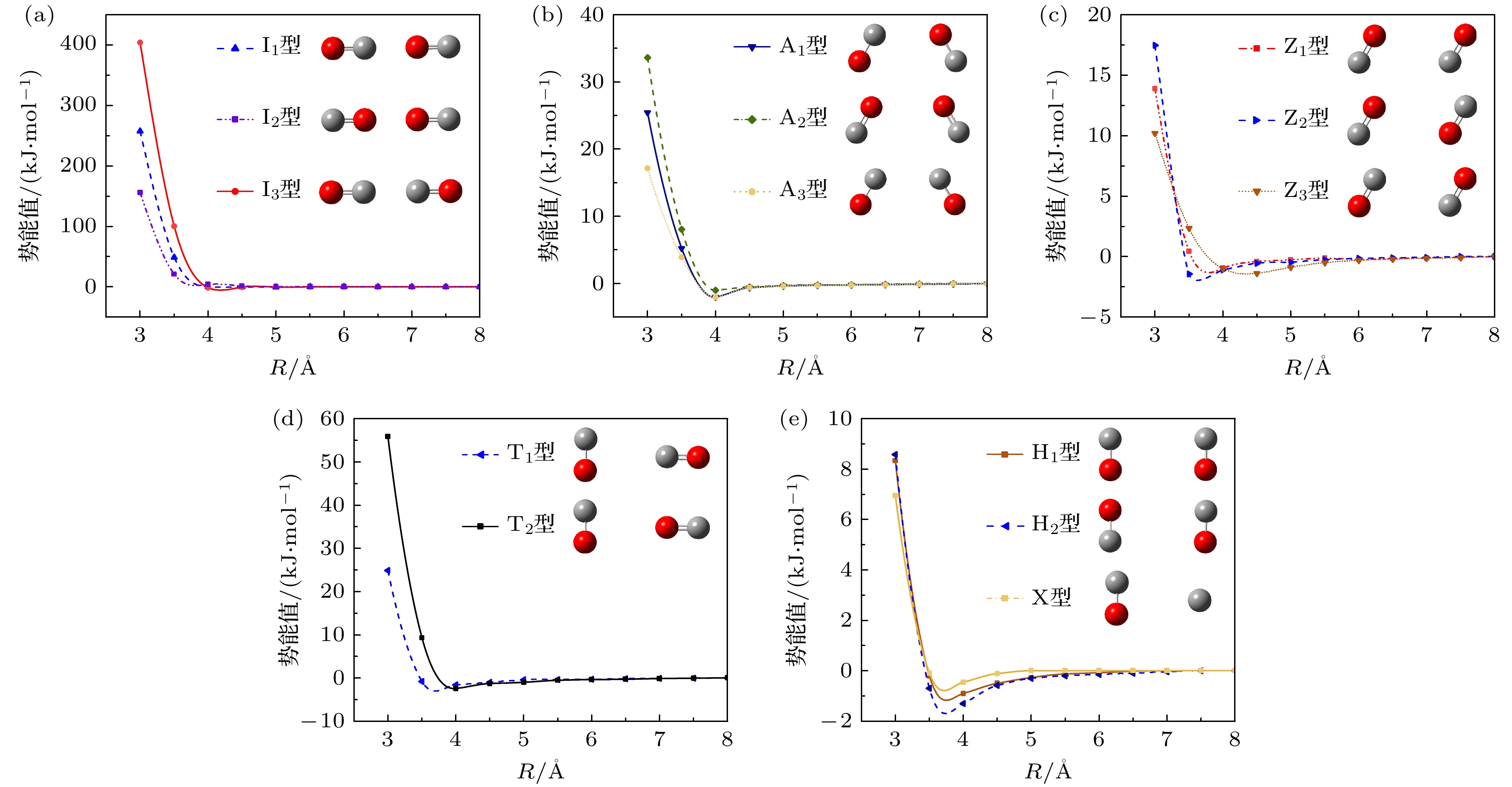
表 1 CO-CO典型构型对应势函数的拟合系数
Table 1. Fitting coefficients of the potential function corresponding to the typical configurations of CO-CO.
构型 a b c d e f I1型 2 0 0 1.765×107 0 0 I2型 3.66 0 0 3.188×107 0 0 I3型 1.41 0 0 1.228×107 0 0 A1型 0.48 –0.641 1.025 0.51×106 –0.695×104 0 A2型 0.64 –0.846 1.354 0.674×106 –0.919×104 0 A3型 0.37 –0.432 0.691 0.343×106 –0.468×104 0 Z1型 0.8675 –0.553 0.629 2.15×105 –6.688×103 51.29 Z2型 0.913 –0.674 0.785 3.12×105 –7.341×103 62.32 Z3型 0.878 –0.576 0.701 2.98×105 –6.89×103 58.31 T1型 1.653 –1.986 2.99 1.785×106 –3.642×105 196.8 T2型 3.715 –2.34 3.54 1.987×106 –4.031×105 213.4 H1型 1.23 –3.86 7.87 2134 12 0.42 H2型 1.27 –3.98 7.98 2053.4 –6 10.76 X型 1.395 –4.21 8.09 12310 –321.58 13.32 
下载: 导出CSV
表 2 6种典型构型下LJ势、Morse势、拟合势函数与DFT计算值的误差
Table 2. Errors of the LJ potential, Morse potential, fitted potential, and the values calculated by DFT for six typical configurations.
I1型 A1型 T1型 Z1型 H1型 X型 LJ 势 25.2% 22.53% 18.66% 18.20% 14.8% 10.7% Morse 势 8.49% 8.51% 9.86% 7.73% 8.6% 6.23% Ef 势 2.44% 3.3% 3.9% 1.2% 1.3% 0.35%
下载: 导出CSV
-
[1] 李志辉, 梁杰, 李中华, 李海燕, 吴俊林, 戴金雯, 唐志共 2018 空气动力学学报 36 826
Google Scholar
Li Z H, Liang J, Li Z H, Li H Y, Wu J L, Dai J W, Tang Z G 2018 Acta Aerodyn. Sin. 36 826
Google Scholar
[2] 罗仕超, 张志刚, 柳军, 龚红明, 胡守超, 吴里银, 常雨, 庄宇, 李贤, 黄成扬 2023 力学学报 55 2439
Google Scholar
Luo S C, Zhang Z G, Liu J, Gong H M, Hu S C, Wu L Y, Chang Y, Zhuang N, Li X, Huang C Y 2023 Chin. J. Theor. Appl. Mech. 55 2439
Google Scholar
[3] 邢赫威, 陈占秀, 杨历, 苏瑶, 李源华, 呼和仓 2024 73 094701
Google Scholar
Xing H W, Chen Z X, Yang L, Su Y, Li Y H, Huhe C 2024 Acta Phys. Sin. 73 094701
Google Scholar
[4] Qian X S 1946 J. Math. Phys. 25 247
Google Scholar
[5] 樊菁 2013 力学进展 43 185
Google Scholar
Fan J 2013 Adv. Mech. 43 185
Google Scholar
[6] Bruno D, Frezzotti A, Ghiroldi G P 2015 Phys. Fluids 27 057101
Google Scholar
[7] Tokumasu T, Matsumoto Y 2000 JSME Int J. Ser. B 43 288
Google Scholar
[8] 李锦, 耿湘人, 陈坚强, 江定武 2016 应用数学和力学 37 1403
Google Scholar
Li J, Geng X R, Chen J J, Jiang D W 2016 Appl. Math. Mech. 37 1403
Google Scholar
[9] Valentini P, Zhang C, Schwartzentruber T E 2012 Phys. Fluids 24 106101
Google Scholar
[10] Baidakov V, Protsenko S, Kozlova Z 2012 J. Chem. Phys. 137 164507
Google Scholar
[11] Baidakov V G, Protsenko S P 2014 J. Chem. Phys. 141 114503
Google Scholar
[12] Sharma B, Kumar R 2019 AIP Conf. Proc. 2132 090003
Google Scholar
[13] Parker J G, Adams C E, Stavseth R M 1953 J. Acoust. Soc. Am. 25 263
Google Scholar
[14] Marcy S J 1990 AIAA J. 28 171
Google Scholar
[15] Dukhin A S, Goetz P J 2009 J. Chem. Phys. 130 124519
Google Scholar
[16] Gu Z, Ubachs W 2013 Opt. Lett. 38 1110
Google Scholar
[17] Carnevale E H, Carey C, Larson G 1967 J. Chem. Phys. 47 2829
Google Scholar
[18] 赵宁波, 郑洪涛, 李淑英 2018 哈尔滨工程大学学报 39 60
Google Scholar
Zhao N B, Zheng H T, Li S Y 2018 J. Harbin Eng. Univ. 39 60
Google Scholar
[19] Kubo R 1985 Pure Appl. Chem. 57 201
Google Scholar
[20] Hellmann R 2013 Mol. Phys. 111 387
Google Scholar
[21] Cramer M S 2012 Phys. Fluids 24 066102
Google Scholar
[22] Lu T, Chen F 2013 J. Mol. Model 19 5387
Google Scholar
[23] Kasper P K 2017 J. Phys. Chem. A 121 9092
Google Scholar
[24] Abbaspour M, Goharshadi E K 2006 Chem. Phys. 330 313
Google Scholar
[25] Hong Q Z, Bartolomei M, Coletti C, Lombardi A, Sun Q H, Pirani F 2021 Molecules 26 7152
Google Scholar
[26] Vogel E 2012 Int. J. Thermophys 33 741
Google Scholar
[27] Heck E L, Dickinson A S 1995 Physica A 217 107
Google Scholar
下载:
计量
- 文章访问数: 584
- PDF下载量: 22
- 被引次数: 0
