-
神经细胞的尺寸与太赫兹波的波长处于同一数量级, 因此, 神经细胞可等效为微型介质谐振器从而起到增强细胞内的太赫兹信号的作用. 基于此现象, 本文提出神经细胞弱谐振效应的新概念. 建立了三层结构的球形神经细胞胞体模型, 用太赫兹时域光谱仪系统测量了神经细胞生理液的相对介电常数, 并用双德拜模型对实验结果进行拟合; 利用时域有限差分法对太赫兹波在神经细胞中的传播特性进行研究. 结果表明, 当神经细胞的相对介电常数高于外部媒质时, 太赫兹波可以在神经细胞内部形成弱的谐振峰, 并且随着细胞与外部媒质的相对介电常数差值的减小, 谐振峰会向细胞膜侧偏移, 细胞对太赫兹波的聚焦特性会随着两侧相对介电常数差值的减小而逐渐增强, 这种现象称为弱谐振效应. 同时, 弱谐振效应也表现出与细胞尺寸和频率的相关性. 神经细胞的弱谐振效应在增强细胞内太赫兹信号强度的同时, 也会进一步增强太赫兹信号在神经纤维中的传输. 这些结果为解释太赫兹波与神经细胞的相互作用提供了新模型, 有助于研究太赫兹波在生物神经系统中的传递机制.The size of nerve cell is comparable to the wavelength of terahertz (THz) wave. In this work, a new concept of weak resonance effect of nerve cells is proposed. The permittivity of intracellular fluid is measured experimentally by using a THz-TDS system, and the relationship between the permittivity of nerve cells and the frequency is obtained by fitting the double Debye model. The propagation characteristics of THz waves in nerve cells are studied by finite difference time domain. The results show that when the dielectric constant of nerve cell is higher than that of the external medium, THz wave can be enhanced in the nerve cell. Meanwhile, as the dielectric constant of the external medium increases, the resonance will be close to the cell membrane. And it shows the focusing property of THz waves, as a convex lens does. The weak resonance effect is related to the dielectric constant of the background medium, and increases with the cell size and frequency increasing. These results provide a new model to explain the interaction between THz wave and nerve cells, contributing to the study of the transmission mechanism of THz wave in biological nervous system.
-
Keywords:
- terahertz /
- nerve cell /
- transimission /
- weak resonance effects
[1] Kumar S, Boone K, Tuszynski J, Barclay P, Simon C 2016 Sci. Rep. 6 1
Google Scholar
[2] Liu G, Chang C, Qiao Z, Wu K, Zhu Z, Cui G, Peng W, Tang Y, Li J, Fan C 2019 Adv. Funct. Mater. 29 1807862
Google Scholar
[3] Miccio L, Memmolo P, Merola F, Netti P, Ferraro P 2015 Nat. Commun. 6 1
[4] Johari P, Jornet J M 2017 IEEE Trans. Commun. 66 1579
Google Scholar
[5] Wirdatmadja S, Johari P, Desai A, Bae Y, Stachowiak E K, Stachowiak M K, Jornet J M, Balasubramaniam S 2019 IEEE Trans. Neural Syst. Rehabil. Eng. 27 108
Google Scholar
[6] Wirdatmadja S A, Barros M T, Koucheryavy Y, Jornet J M, Balasubramaniam S 2017 IEEE Trans. Nanobiosci. 16 859
Google Scholar
[7] Akyildiz I F, Brunetti F, Blázquez C 2008 Comput. Networks 52 2260
Google Scholar
[8] Lee S T, Williams P A, Braine C E, Lin D T, John S, Irazoqui P P 2015 IEEE Trans. Neural Syst. Rehabil. Eng. 23 655
Google Scholar
[9] Khattak H K, Bianucci P, Slepkov A D 2019 Proc. Natl. Acad. Sci. 116 4000
Google Scholar
[10] Nagai M, Yada H, Arikawa T, Tanaka K 2006 Int. J. Infrared Millimeter Waves 27 505
[11] Paparo D, Tielrooij K J, Bakker H, Bonn M 2009 Mol. Cryst. Liq. Cryst. 500 108
Google Scholar
[12] Zhou J, Rao X, Liu X, Li T, Zhou L, Zheng Y, Zhu Z 2019 AIP Adv. 9 035346
Google Scholar
[13] Brown W, Needham K, Nayagam B A, Stoddart P R 2013 J. Vis. Exp. 77 50444
Google Scholar
[14] Kindt J T, Schmuttenmaer C A 1996 J. Phys. Chem. 100 10373
Google Scholar
[15] Yee K 1966 IEEE Trans. Antennas Propag. 14 302
Google Scholar
[16] Wei B, Zhang S Q, Wang F, Ge D 2010 Waves Random Complex Media 20 511
Google Scholar
[17] Zhou Y, Wei B, Yin P 2011 IEEE International Conference on Microwave Technology & Computational Electromagneticsed Beijing, China, May 22–25, 2011 402
[18] Zeng Q, Michael I P, Zhang P, Saghafinia S, Knott G, Jiao W, McCabe B D, Galván J A, Robinson H P C, Zlobec I 2019 Nature 573 526
Google Scholar
[19] Fitzgerald A J, Pickwell-MacPherson E, Wallace V P 2014 PLoS One 9 e99291
Google Scholar
-
图 1 细胞膜、细胞内生理液和细胞核三层媒质构建的神经细胞体模型
Fig. 1. Nerve cell body model constructed by three layers of membrane, intracellular fluid and nucleus.
图 2 等效细胞内生理液体在0.3−2 THz频率范围内的(a) 吸收系数, (b)折射率, (c)相对介电常数实部和虚部(黑色圆点)以及二阶德拜模型拟合结果(红色实线)
Fig. 2. (a) Absorption coefficient, (b) refractive index, and (c) the real and imaginary parts of the dielectric constant of the effective intracellular fluid in the frequency range of 0.3−2 THz.
图 3 由二阶德拜模型模拟等效细胞内生理液在0.3−50 THz范围内的相对介电常数 (a)实部; (b)虚部
Fig. 3. Dielectric constant of intracellular fluid in the range of 0.3−50 THz simulated by second-order Debye model: (a) Real part; (b) imaginary part.
图 4 (a)太赫兹波在神经细胞中传输的三维FDTD模型, 太赫兹波由线源产生, 以柱面波的形式向三维空间传输; (b)模拟过程中用到的3种频率(20, 25, 30 THz)的太赫兹辐射源波形
Fig. 4. (a) Three-dimensional FDTD model of THz wave transmission in the nerve cell. THz wave is generated by line sources and transmitted to three-dimensional space in the form of cylindrical wave. (b) THz source waveforms for the three frequencies (20, 25, 30 THz) used in the simulation.
图 5 曲面边界的梯形网格处理方法, 橙色的区域是细胞膜
Fig. 5. Surface boundary trapezoidal mesh treatment, the orange area is the cell membrane.
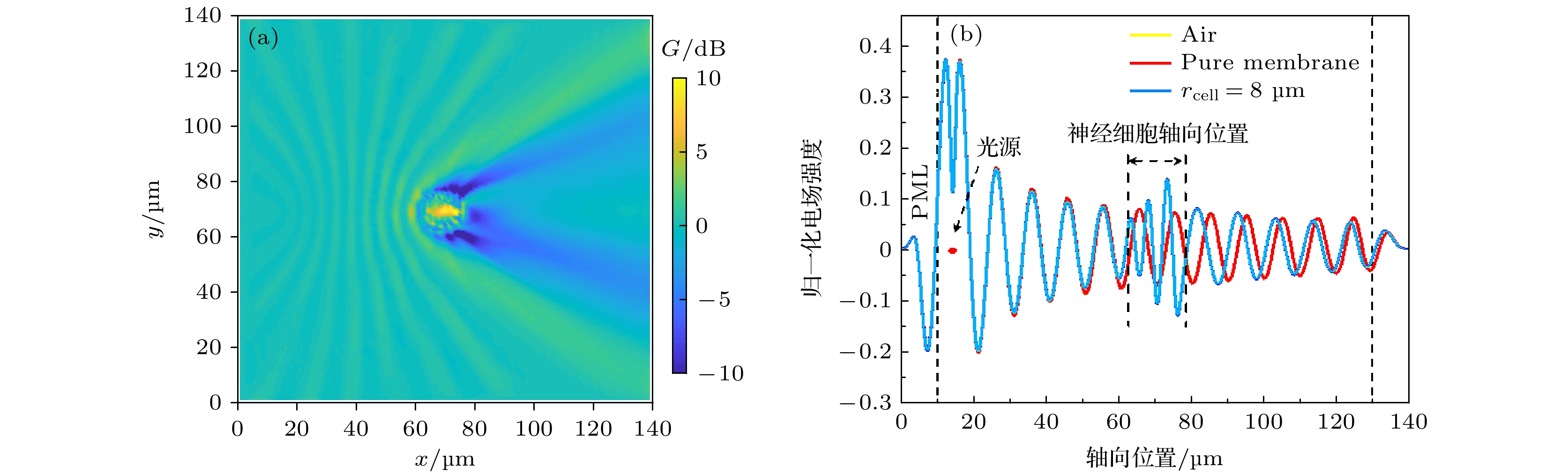
图 6 (a)频率为30 THz的太赫兹波在神经细胞中传输的增益G; (b)太赫兹波在空气(黄色曲线)中、无神经细胞内生理液的模型(红色曲线)以及含有神经细胞内生理液的细胞模型(蓝色曲线)的一维场分布结果, 其中黄色曲线与红色曲线发生重叠
Fig. 6. (a) Gain of the THz wave transmission in nerve cells at a frequency of 30 THz; (b) one-dimensional field distribution results of the THz wave in air (yellow curve), a model without intracellular fluid (red curve), and a cell model with intracellular fluid (blue curve). The yellow curve overlaps with the red curve.
图 7 (a)—(f)背景媒质的相对介电常数分别为1, 2, 3, 4, 5和6时, 神经细胞中的场增益G结果, 太赫兹波的频率为30 THz
Fig. 7. (a)−(f) Field gain results in the nerve cell when the dielectric constant of background medium is 1, 2, 3, 4, 5, 6. The frequency is 30 THz.
图 8 背景媒质的相对介电常数分别为1, 2, 3, 4, 5和6时, 频率为30 THz的太赫兹波在神经细胞中轴线上的增益G曲线
Fig. 8. Gain curves on axis when dielectric constant of background medium is 1, 2, 3, 4, 5, 6, and the frequency is 30 THz.
图 9 背景媒质为乳腺和癌变的乳腺组织时, 频率为30 THz的太赫兹波在神经细胞中的(a)电场分布和(b)轴线上的增益
Fig. 9. (a) Electric field distribution and (b) gain of the 30 THz terahertz wave in nerve cells under the condition of breast and cancerous breast tissue in the background medium.
图 10 (a)—(c)神经细胞的半径为8, 12.5和20 µm时, 太赫兹波在神经细胞中传输的增益G
Fig. 10. (a)−(c) Gain of THz wave transmission in nerve cells with the radius of 8, 12.5, 20 µm.
图 11 神经细胞的半径为8, 12.5和20 µm时, 轴线上的场增益曲线
Fig. 11. Field gain curves along the axis of nerve cells with radius of 8, 12.5 and 20 µm.
图 12 3种不同频率的太赫兹波通过神经元细胞传播的特性 (a) 20 THz; (b) 25 THz; (c) 30 THz
Fig. 12. Characteristic of three THz waves of different frequencies transmitting through the neuron cell: (a) 20 THz; (b) 25 THz; (c) 30 THz.
图 13 神经细胞弱谐振效应与太赫兹波频率的关系, 细胞中心位于70 μm处
Fig. 13. Relation between weak resonance effect and THz frequency of nerve cells, cell center at 70 μm.
图 14 背景媒质的相对介电常数为(a) 2, (b) 4时, 神经细胞-轴突模型中的场增益G结果
Fig. 14. Field gain results in the neuron-axon model, when the relative permittivity of background medium is (a) 2 and (b) 4.
表 1 细胞膜二阶德拜模型参数拟合结果
Table 1. Fitting results of membrane second-order Debye model parameters.
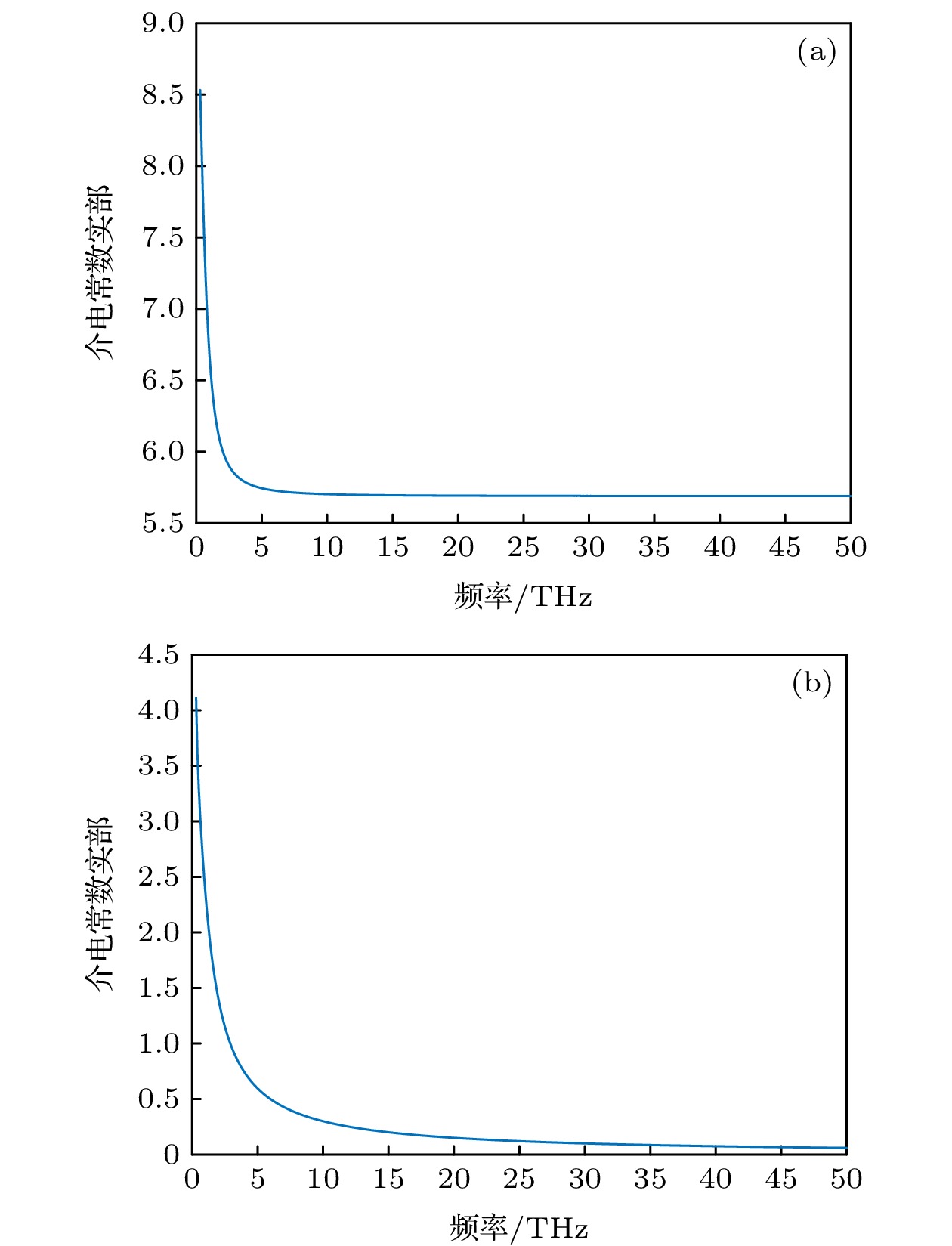
$ {\varepsilon }_{\infty } $ $ {\varepsilon }_{\mathrm{s}} $ $ {\varepsilon }_{2} $ $ {\tau }_{1} $/ps $ {\tau }_{2} $/ps 细胞膜 2.37 11.77 3.28 7.19 0.11 
下载: 导出CSV
表 2 等效神经细胞内生理液相对介电常数的二阶德拜模型参数拟合结果
Table 2. Second-order Debye model parameter fitting results of dielectric constant of the effective intracellular fluid in nerve cells.
$ {\varepsilon }_{\infty } $ $ {\varepsilon }_{\mathrm{s}} $ $ {\varepsilon }_{2} $ $ {\tau }_{1} $/ps $ {\tau }_{2} $/ps 细胞内生理液 5.685 77.34 8.990 12.6 0.243
下载: 导出CSV
表 3 正常的乳腺组织以及癌变的乳腺组织的二阶德拜模型参数
Table 3. Second-order Debye model parameters of normal and cancerous breast tissues.
$ {\varepsilon }_{\infty } $ $ {\varepsilon }_{\mathrm{s}} $ $ {\varepsilon }_{2} $ $ {\tau }_{1} $/ps $ {\tau }_{2} $/ps 正常乳腺组织 2.1 76.5 3.9 10.3 0.07 癌变乳腺组织 2.5 77.9 4.3 9.1 0.08
下载: 导出CSV
-
[1] Kumar S, Boone K, Tuszynski J, Barclay P, Simon C 2016 Sci. Rep. 6 1
Google Scholar
[2] Liu G, Chang C, Qiao Z, Wu K, Zhu Z, Cui G, Peng W, Tang Y, Li J, Fan C 2019 Adv. Funct. Mater. 29 1807862
Google Scholar
[3] Miccio L, Memmolo P, Merola F, Netti P, Ferraro P 2015 Nat. Commun. 6 1
[4] Johari P, Jornet J M 2017 IEEE Trans. Commun. 66 1579
Google Scholar
[5] Wirdatmadja S, Johari P, Desai A, Bae Y, Stachowiak E K, Stachowiak M K, Jornet J M, Balasubramaniam S 2019 IEEE Trans. Neural Syst. Rehabil. Eng. 27 108
Google Scholar
[6] Wirdatmadja S A, Barros M T, Koucheryavy Y, Jornet J M, Balasubramaniam S 2017 IEEE Trans. Nanobiosci. 16 859
Google Scholar
[7] Akyildiz I F, Brunetti F, Blázquez C 2008 Comput. Networks 52 2260
Google Scholar
[8] Lee S T, Williams P A, Braine C E, Lin D T, John S, Irazoqui P P 2015 IEEE Trans. Neural Syst. Rehabil. Eng. 23 655
Google Scholar
[9] Khattak H K, Bianucci P, Slepkov A D 2019 Proc. Natl. Acad. Sci. 116 4000
Google Scholar
[10] Nagai M, Yada H, Arikawa T, Tanaka K 2006 Int. J. Infrared Millimeter Waves 27 505
[11] Paparo D, Tielrooij K J, Bakker H, Bonn M 2009 Mol. Cryst. Liq. Cryst. 500 108
Google Scholar
[12] Zhou J, Rao X, Liu X, Li T, Zhou L, Zheng Y, Zhu Z 2019 AIP Adv. 9 035346
Google Scholar
[13] Brown W, Needham K, Nayagam B A, Stoddart P R 2013 J. Vis. Exp. 77 50444
Google Scholar
[14] Kindt J T, Schmuttenmaer C A 1996 J. Phys. Chem. 100 10373
Google Scholar
[15] Yee K 1966 IEEE Trans. Antennas Propag. 14 302
Google Scholar
[16] Wei B, Zhang S Q, Wang F, Ge D 2010 Waves Random Complex Media 20 511
Google Scholar
[17] Zhou Y, Wei B, Yin P 2011 IEEE International Conference on Microwave Technology & Computational Electromagneticsed Beijing, China, May 22–25, 2011 402
[18] Zeng Q, Michael I P, Zhang P, Saghafinia S, Knott G, Jiao W, McCabe B D, Galván J A, Robinson H P C, Zlobec I 2019 Nature 573 526
Google Scholar
[19] Fitzgerald A J, Pickwell-MacPherson E, Wallace V P 2014 PLoS One 9 e99291
Google Scholar
下载:
计量
- 文章访问数: 7233
- PDF下载量: 192
- 被引次数: 0
