-
极化指的是波偏振的方式, 是波的一个基本性质. 利用波的极化可以进行信息的编码, 这一编码方式在光学和声学中得到广泛应用. 利用自旋波进行信息的传递和处理是磁子学的主要研究课题. 然而在铁磁材料中, 由于只存在右旋极化的自旋波, 利用波的极化进行信息的编码在铁磁自旋波器件中始终没有实现. 前期研究发现, 通过自旋极化电流可以在铁磁体中产生左旋极化自旋波, 从而有望实现利用极化编码的自旋波器件. 然而在一个均匀磁化铁磁体中产生左旋极化自旋波所需的电流密度过大, 实验上难以实现. 磁畴壁可作为自旋波波导, 且畴壁中自旋波的截止频率趋近于零. 本文从朗道-栗弗席兹方程出发, 研究了在自旋极化电流存在的条件下磁畴壁中自旋波的色散关系和传播特性, 证明只需要很小的自旋极化电流就可在畴壁中产生稳定的左旋极化自旋波. 微磁学模拟证明了理论分析结果. 该项研究为研制基于极化编码信息的自旋波器件提供了一个实际可行的方案.Polarization refers to the orientation of the wave oscillation which is a fundamental property of wave. It has been used widely to encode information in photonics and phononics. In magnonics, spin wave also has been used for transmitting and processing information. However, exploiting the spin wave polarization to design devices has not been achieved yet in ferromagnets as only the right-handed polarized spin waves can be accommodated in ferromagnets. Our eariler study suggests that the left-handed polarized spin waves can be introduced into ferromagnets by appling a spin-polarized electric current, thus making it possible to design spin wave devices with polarization encoding. But the critical current needed to induce left-handed polarized spin wave in a uniformly magnetized ferromagnet is too high to be realized experimentally. Magnetic domain wall can serve as spin wave guide, and the cutoff frequency of spin wave in a domain wall approaches zero. In this work, the dispersion relationship and propagation characteristics of spin wave in a Bloch domain wall are studied based on the Landau-Lifshitz equation in the presence of a spin-polarized electrical current. It is found that the stable left-handed spin wave can be generated in the domain wall with only a small current density. Micromagnetic simulations confirm the theoretical analysis results. In addition, due to the different excitation efficiencies and spin transfer torque induced propagating nonreciprocity of left- and right-handed polarized spin wave, it is possible to excite selectively the left- and right-handed polarized spin wave, as well as nearly linearly polarized spin waves. This study provides a practical and feasible solution for designing spin wave devices based on the polarization coding technique.
-
Keywords:
- spin wave /
- magnetic domain wall /
- spin-polarized electric current /
- micromagnetics
[1] Bloch, Zur F 1930 Z. Phys. 61 206
Google Scholar
[2] Kostylev M P, Serga A A, Schneider T, Leven B, Hillebrands B 2005 Appl. Phys. Lett. 871 53501
Google Scholar
[3] Khitun A, Wang K L 2005 Superlatt. Microstruct. 38 184
Google Scholar
[4] Chumak A V, Serga A A, Hillebrands B 2014 Nat. Commun. 5 4700
Google Scholar
[5] Khitun A, Bao M, Wang K L 2010 J. Phys. D 43 264005
Google Scholar
[6] Khitun A, Wang K L 2011 J. Appl. Phys. 110 034306
Google Scholar
[7] Klingler S, Pirro P, Brächer T, Leven B, Hillebrands B, Chumak A V 2014 Appl. Phys. Lett. 105 152410
Google Scholar
[8] Au Y, Ahmad E, Dmytriiev O, Dvornik M, Davison T, Kruglyak V V 2012 Appl. Phys. Lett. 100 182404
Google Scholar
[9] Demidov V E, Kostylev M P, Rott K, Münchenberger J, Reiss G, Demokritov S O 2011 Appl. Phys. Lett. 99 082507
Google Scholar
[10] Yan J, Ren Z W, Zhong Z Y 2021 Acta Phys. Sin. 70 187501 [闫健, 任志伟, 钟智勇 2021 70 187501]
Google Scholar
Yan J, Ren Z W, Zhong Z Y 2021 Acta Phys. Sin. 70 187501
Google Scholar
[11] Shen R C, Zhang G Q, Wang Y P, You J Q 2019 Acta Phys. Sin. 68 230305 [沈瑞昌, 张国强, 王逸璞, 游建强 2019 68 230305]
Google Scholar
Shen R C, Zhang G Q, Wang Y P, You J Q 2019 Acta Phys. Sin. 68 230305
Google Scholar
[12] Owens J M, Collins J H, Carter R L 1985 Circuits Syst. Signal Process 4 317
Google Scholar
[13] Adam J D 1988 Proc. IEEE 76 159
Google Scholar
[14] Hirsch J E 1999 Phys. Rev. Lett. 83 1834
Google Scholar
[15] Uchida K, Takahashi S, Harii K, Ieda J, Koshibae W, Ando K, Maekawa S, Saitoh E 2008 Nature 455 778
Google Scholar
[16] Demokritov S O, Serga A A, Andre A, Demidov V E, Kostylev M P, Hillebrands B, Slavin A N 2004 Phys. Rev. Lett. 93 047201
Google Scholar
[17] Vlaminck V, Bailleul M 2008 Science 322 410
Google Scholar
[18] Seo S M, Lee K J, Yang H, Ono T 2009 Phys. Rev. Lett. 102 147202
Google Scholar
[19] Hamadeh A, Kelly O A, Hahn C, Meley H, Bernard R, Molpeceres A H, Naletov V V, Viret M, Anane A, Cros V, Demokritov S O, Prieto J L, Muñoz M, De L G, Klein O 2014 Phys. Rev. Lett. 113 197203
Google Scholar
[20] Rousseau O, Rana B, Anami R, Yamada M, Miura K, Ogawa S, Otani Y 2015 Sci. Rep. 5 9873
Google Scholar
[21] Bennett C H, DiVincenzo D P 2000 Nature 404 247
Google Scholar
[22] Sophia R S, Jeffrey C G 2014 New J. Phys. 16 053029
Google Scholar
[23] Sklan S R 2015 AIP Adv. 5 053302
Google Scholar
[24] Kim S K, Hill D, Tserkovnyak Y 2016 Phys. Rev. Lett. 117 237201
Google Scholar
[25] Cheng R, Daniels M W, Zhu J G, Xiao D 2016 Sci. Rep. 6 24223
Google Scholar
[26] Lan J, Yu W, Xiao J 2017 Nat. Commun. 8 178
Google Scholar
[27] Zhou Z W, Wang X G, Nie Y Z, Xia Q L, Zeng Z M, Guo G H 2019 Phys. Rev. B 99 014420
Google Scholar
[28] Zhang S, Li Z 2004 Phys. Rev. Lett. 93 127204
Google Scholar
[29] Garcia-Sanchez F, Borys P, Soucaille R, Adam J, Stamps R L, Kim J 2015 Phys. Rev. Lett. 114 247206
Google Scholar
[30] Lan J, Yu W C, Wu R Q, Xiao J 2015 Phys. Rev. X 5 041049
[31] Wagner K, Kákay A, Schultheiss K, Henschke A, Sebastian T, Schultheiss H 2016 Nat. Nanotech. 11 432
Google Scholar
[32] Zhao M, Wang X G, Luo Z Y, Xia Q L, Nie Y Z, Xiong R, Guo G H 2022 Phys. Rev. Appl. 17 064013
Google Scholar
[33] Mougin A, Cormier M, Adam J P, Metaxas P J, Ferré J 2007 Europhys. Lett. 78 57007
Google Scholar
[34] Schryer N L, Walker L R 1974 J. Appl. Phys. 45 5406
Google Scholar
[35] Winter J M 1961 Phys. Rev. 124 452
Google Scholar
[36] Ravelosona D, Cebollada A, Briones F, Diaz-Paniagua C, Hidalgo M A, Batallan F 1999 Phys. Rev. B 59 4322
Google Scholar
[37] Yu T, Wang C, Sentef M A, Bauer G E W 2021 Phys. Rev. Lett. 126 137202
Google Scholar
[38] He J X, Zhang S F 2008 Phys. Rev. B 78 012414
Google Scholar
[39] Dolocan V O 2012 Appl. Phys. Lett. 101 072409
Google Scholar
[40] Nakatani Y, Shibata J, Tatara G, Kohno H, Thiaville A, Miltat J 2008 Phys. Rev. B 77 014439
Google Scholar
[41] Tserkovnyak Y, Skadsem H J, Brataas A, Bauer G E W 2006 Phys. Rev. B 74 144405
Google Scholar
[42] Vansteenkiste A, Leliaert J, Dvornik M, Garcia-sanchez F, Waeyenberge B V 2014 AIP Adv. 4 107133
Google Scholar
[43] Yan Z M , Li Z X, Wang X G, Luo Z Y, Xia Q L, Nie Y Z, Guo G H 2023 Phys. Rev. B 108 134432
Google Scholar
-
图 1 垂直磁各向异性铁磁纳米带中布洛赫畴壁的示意图, 绿色部分表示激发场施加的区域
Fig. 1. Schematic diagram of Bloch magnetic domain wall in a ferromagnetic thin film with perpendicular magnetic anisotropy, the green shaded area represents the place where the excitation field is applied.
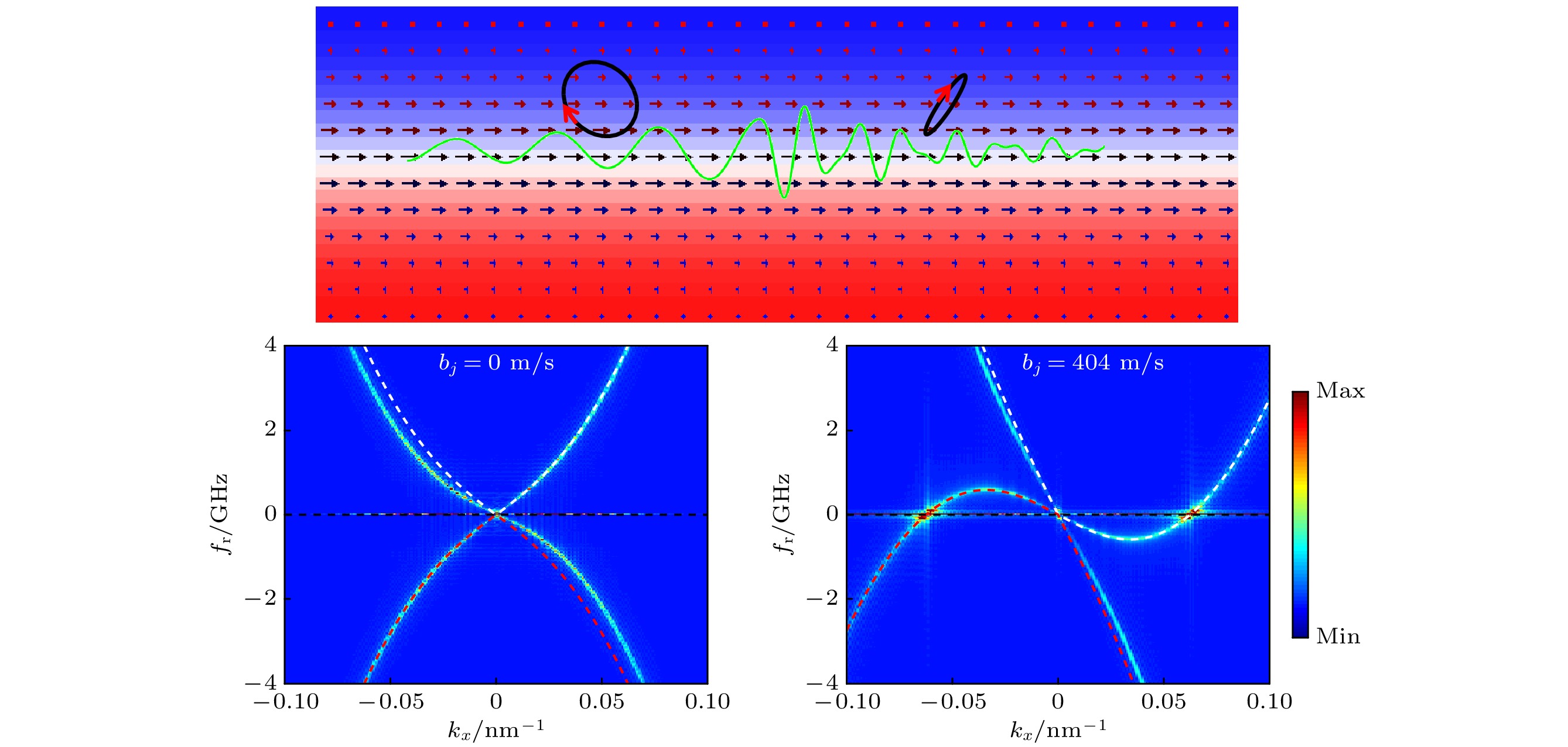
图 2 畴壁中自旋波的色散关系曲线 (a) bj = 0; (b)bj = 404 m/s; 蓝色实线和绿色(红色)虚线分别表示微磁学模拟结果和理论公式计算结果, 其中绿色虚线和红色虚线分别对应右旋和左旋自旋波的色散关系
Fig. 2. Dispersion relations of spin waves in domain wall for (a) bj = 0 and (b) bj = 404 m/s. The blue solid lines and green (red) dashed lines represent the results of micromagnetic simulations and theoretical calculations, respectively. The green and the red dashed lines correspond to the dispersion relations of right-handed and left-handed spin waves, respectively.
图 3 自旋波波形图和空间傅里叶变换 (a) 线偏振场激发, bj = 404 m/s, f = 2 GHz; (b) 线偏振场激发, bj = 404 m/s, f = 0.5 GHz; (c) 左旋圆偏振场激发, bj = 404 m/s, f = 0.5 GHz; (d)—(f) 与(a)—(c)自旋波波形图对应的空间傅里叶变换, 图中红色箭头为磁化矢量的进动方向
Fig. 3. Spin waveforms and spatial Fourier transformation: (a) Spin waves excited by a linear polarization harmonic field with f = 2 GHz, bj = 404 m/s; (b) spin waves excited by a linear polarization harmonic field with f = 0.5 GHz, bj = 404 m/s; (c) spin wavese excited by a left circular polarization field with f = 0.5 GHz, bj = 404 m/s; (d)–(f) the spatial Fourier transformations corresponding to (a)–(c), respectively, the red arrows in the figure represent the precession direction of the magnetization vector.
-
[1] Bloch, Zur F 1930 Z. Phys. 61 206
Google Scholar
[2] Kostylev M P, Serga A A, Schneider T, Leven B, Hillebrands B 2005 Appl. Phys. Lett. 871 53501
Google Scholar
[3] Khitun A, Wang K L 2005 Superlatt. Microstruct. 38 184
Google Scholar
[4] Chumak A V, Serga A A, Hillebrands B 2014 Nat. Commun. 5 4700
Google Scholar
[5] Khitun A, Bao M, Wang K L 2010 J. Phys. D 43 264005
Google Scholar
[6] Khitun A, Wang K L 2011 J. Appl. Phys. 110 034306
Google Scholar
[7] Klingler S, Pirro P, Brächer T, Leven B, Hillebrands B, Chumak A V 2014 Appl. Phys. Lett. 105 152410
Google Scholar
[8] Au Y, Ahmad E, Dmytriiev O, Dvornik M, Davison T, Kruglyak V V 2012 Appl. Phys. Lett. 100 182404
Google Scholar
[9] Demidov V E, Kostylev M P, Rott K, Münchenberger J, Reiss G, Demokritov S O 2011 Appl. Phys. Lett. 99 082507
Google Scholar
[10] Yan J, Ren Z W, Zhong Z Y 2021 Acta Phys. Sin. 70 187501 [闫健, 任志伟, 钟智勇 2021 70 187501]
Google Scholar
Yan J, Ren Z W, Zhong Z Y 2021 Acta Phys. Sin. 70 187501
Google Scholar
[11] Shen R C, Zhang G Q, Wang Y P, You J Q 2019 Acta Phys. Sin. 68 230305 [沈瑞昌, 张国强, 王逸璞, 游建强 2019 68 230305]
Google Scholar
Shen R C, Zhang G Q, Wang Y P, You J Q 2019 Acta Phys. Sin. 68 230305
Google Scholar
[12] Owens J M, Collins J H, Carter R L 1985 Circuits Syst. Signal Process 4 317
Google Scholar
[13] Adam J D 1988 Proc. IEEE 76 159
Google Scholar
[14] Hirsch J E 1999 Phys. Rev. Lett. 83 1834
Google Scholar
[15] Uchida K, Takahashi S, Harii K, Ieda J, Koshibae W, Ando K, Maekawa S, Saitoh E 2008 Nature 455 778
Google Scholar
[16] Demokritov S O, Serga A A, Andre A, Demidov V E, Kostylev M P, Hillebrands B, Slavin A N 2004 Phys. Rev. Lett. 93 047201
Google Scholar
[17] Vlaminck V, Bailleul M 2008 Science 322 410
Google Scholar
[18] Seo S M, Lee K J, Yang H, Ono T 2009 Phys. Rev. Lett. 102 147202
Google Scholar
[19] Hamadeh A, Kelly O A, Hahn C, Meley H, Bernard R, Molpeceres A H, Naletov V V, Viret M, Anane A, Cros V, Demokritov S O, Prieto J L, Muñoz M, De L G, Klein O 2014 Phys. Rev. Lett. 113 197203
Google Scholar
[20] Rousseau O, Rana B, Anami R, Yamada M, Miura K, Ogawa S, Otani Y 2015 Sci. Rep. 5 9873
Google Scholar
[21] Bennett C H, DiVincenzo D P 2000 Nature 404 247
Google Scholar
[22] Sophia R S, Jeffrey C G 2014 New J. Phys. 16 053029
Google Scholar
[23] Sklan S R 2015 AIP Adv. 5 053302
Google Scholar
[24] Kim S K, Hill D, Tserkovnyak Y 2016 Phys. Rev. Lett. 117 237201
Google Scholar
[25] Cheng R, Daniels M W, Zhu J G, Xiao D 2016 Sci. Rep. 6 24223
Google Scholar
[26] Lan J, Yu W, Xiao J 2017 Nat. Commun. 8 178
Google Scholar
[27] Zhou Z W, Wang X G, Nie Y Z, Xia Q L, Zeng Z M, Guo G H 2019 Phys. Rev. B 99 014420
Google Scholar
[28] Zhang S, Li Z 2004 Phys. Rev. Lett. 93 127204
Google Scholar
[29] Garcia-Sanchez F, Borys P, Soucaille R, Adam J, Stamps R L, Kim J 2015 Phys. Rev. Lett. 114 247206
Google Scholar
[30] Lan J, Yu W C, Wu R Q, Xiao J 2015 Phys. Rev. X 5 041049
[31] Wagner K, Kákay A, Schultheiss K, Henschke A, Sebastian T, Schultheiss H 2016 Nat. Nanotech. 11 432
Google Scholar
[32] Zhao M, Wang X G, Luo Z Y, Xia Q L, Nie Y Z, Xiong R, Guo G H 2022 Phys. Rev. Appl. 17 064013
Google Scholar
[33] Mougin A, Cormier M, Adam J P, Metaxas P J, Ferré J 2007 Europhys. Lett. 78 57007
Google Scholar
[34] Schryer N L, Walker L R 1974 J. Appl. Phys. 45 5406
Google Scholar
[35] Winter J M 1961 Phys. Rev. 124 452
Google Scholar
[36] Ravelosona D, Cebollada A, Briones F, Diaz-Paniagua C, Hidalgo M A, Batallan F 1999 Phys. Rev. B 59 4322
Google Scholar
[37] Yu T, Wang C, Sentef M A, Bauer G E W 2021 Phys. Rev. Lett. 126 137202
Google Scholar
[38] He J X, Zhang S F 2008 Phys. Rev. B 78 012414
Google Scholar
[39] Dolocan V O 2012 Appl. Phys. Lett. 101 072409
Google Scholar
[40] Nakatani Y, Shibata J, Tatara G, Kohno H, Thiaville A, Miltat J 2008 Phys. Rev. B 77 014439
Google Scholar
[41] Tserkovnyak Y, Skadsem H J, Brataas A, Bauer G E W 2006 Phys. Rev. B 74 144405
Google Scholar
[42] Vansteenkiste A, Leliaert J, Dvornik M, Garcia-sanchez F, Waeyenberge B V 2014 AIP Adv. 4 107133
Google Scholar
[43] Yan Z M , Li Z X, Wang X G, Luo Z Y, Xia Q L, Nie Y Z, Guo G H 2023 Phys. Rev. B 108 134432
Google Scholar
下载:
计量
- 文章访问数: 1627
- PDF下载量: 71
- 被引次数: 0
