HL-2A高约束先进运行模式等离子体电流剖面集成模拟

张洪铭; 吴静; 李佳鲜; 姚列明; 徐江城; 吴岩占; 刘旗艳; 郭鹏程

doi:10.7498/aps.70.20210945

摘要

磁约束托卡马克装置等离子体物理参数, 如等离子体电流、约束磁场、安全因子的实时监测对高约束模式(H模)的稳态运行至关重要. 本文介绍了基于HL-2A实验数据和集成建模手段, 重建先进高约束运行模式(H模)下等离子体位形, 电流密度和安全因子参数剖面. 通过搭建动力学平衡位形集成模拟平台, 结合工作流快速处理手段, 采用真实实验数据和集成模拟模型, 得到了HL-2A高约束模式放电条件的离子和电子温度、密度, 电流密度和安全因子q剖面, 重建了高约束模式放电物理图像和托卡马克内部磁面位形和等离子体边界参数连续分布, 计算了等离子体欧姆电流、自举电流和射频电流等剖面及各自份额, 给出了先进运行模式下安全因子q径向分布. 通过集成模拟, 发现HL-2A该炮号参数条件下台基宽度约7.52 cm, 压强梯度的方向在ρ(r/a) = 0.1改变, 在ρ = 0.7附近数值达到最大, 可能是负剪切产生的内部输运垒位形(ITB)引起的. 通过等离子体磁场和电流等剖面重建和实时监测, 可以评估HL-2A高约束放电实验的品质, 为HL-2M高比压（β_n）先进模式的稳态运行提供参考.

关键词:

HL-2A /
OMFIT平台 /
集成建模框架

Abstract

The plasma current (I_p), magnetic field (B), and safety factor distribution (q profile) of the HL-2A tokamak device are crucial to monitoring the steady-state operational scenarios (in high confinement mode, H mode). Based on real experimental data and integrated modeling simulation method (OMFIT), the plasma parameters’ profiles such as magnetic field configuration and current density profiles in H mode were reconstructed. By building up an integrated simulation platform for dynamic equilibrium configuration, and combining the rapid workflow processing method and experimental data with integrated simulation models, the ion and electron temperature, density, and current density profiles were obtained. The integration simulation platform was established to reconstruct the internal magnetic surface configuration, the plasma boundary parameter distribution, the ion/electron temperature, current density, and the q profile. The Ohmic current, bootstrap current, and radio-frequency current profiles with its fractions were calculated. The width of the pedestal region was about 7.52 cm according to our simulation results. It was found that the pressure gradient changes its direction at radial coordinate ρ(r/a) = 0.1 and reaches its maximum value near ρ = 0.7, which may be the internal transport barrier (ITB) configuration caused by negative shear. The profile reconstruction and real-time monitoring of the physical parameters are conducive to evaluating the quality of H mode discharge experiment and can assist in the steady-state operation of advanced operating modes such as HL-2M high normalized beta (β_n) discharge.

Keywords:

作者及机构信息

1.
电子科技大学物理学院, 成都　611731

2.
核工业西南物理研究院聚变研究所, 成都　610225

通信作者: 吴静, wujing@uestc.edu.cn ; 李佳鲜, lijx@swip.ac.cn ; 姚列明, ylm@uestc.edu.cn ;

基金项目: 国家重点研发计划(批准号: 2019YFE03020004)资助的课题

Authors and contacts

1.
School of Physics, University of Electronic Science and Technology of China, Chengdu 611731, China

2.
Fusion Research Institute, Southwestern Institute of Physics, Chengdu 610225, China

Corresponding author: Wu Jing, wujing@uestc.edu.cn ; Li Jia-Xian, lijx@swip.ac.cn ; Yao Lie-Ming, ylm@uestc.edu.cn ;

Funds: Project supported by the National Key Research and Development Program of China (Grant No. 2019YFE03020004).

文章全文 : translate this paragraph

参考文献

[1]	Wagner F 1982 Phys. Re. Lett. 49 1408 Google Scholar
[2]	李凯 2020 博士学位论文 (合肥: 中国科学技术大学) Li K 2020 Ph. D. Dissertation (Hefei: University of Science and Technology of China) (in Chinese)
[3]	钟武律, 段旭如 2020 原子核物理评论 37 462 Google Scholar Zhong W L, Duan X R 2020 Nucl. Phys. Re. 37 462 Google Scholar
[4]	Snyder P B, Aiba N, Beurskens M 2009 Nucl. Fusion 49 085035 Google Scholar
[5]	Stacey W M, Groebner R J 2003 Phys. Plasm. 10 2412 Google Scholar
[6]	Lao L L, Ferron J R, Groebner R J, et al. 1990 Nucl. Fusion 30 103549
[7]	Fellinger P, Marklein R, Langenberg K J, Klaholz S 1995 Wave Motion 21 47 Google Scholar
[8]	陈文锦, 何小雪, 刘亮, 魏彦玲, 马倩, 余德良 2016 核聚变与等离子体物理 36 104 Google Scholar Chen W J, He X X, Liu L, Wei Y L, Ma Q, Yu D L 2016 Nucl. Fusion Plasma Phys. 36 104 Google Scholar
[9]	Logan N C, Grierson, B A, Haskey S R, Smith S P, Meneghini O, Eldon D 2018 Nucl. Fusion 74 125 Google Scholar
[10]	Meneghini O, Lao L 2013 Plasma Fusion Res. 8 2403009 Google Scholar
[11]	Meneghini O, Smith S P, Lao L L, Izacard O, et al. 2015 Nucl. Fusion 55 083008 Google Scholar
[12]	吴木泉 2020 博士学位论文 (合肥: 中国科学技术大学) Wu M Q 2020 Ph. D. Dissertation (Hefei: University of Science and Technology of China) (in Chinese)
[13]	李强 2009 原子能科学技术 S2 204 Li Q 2009 Atomic Energy Sci. Technol. S2 204 (in Chinese)
[14]	饶军, 陆志鸿, 张劲松等 2009 核聚变与等离子体物理 29 324 Google Scholar Rao J, Lu Z H, Zhang J S, et al. 2009 Nucl. Fusion Plasma Phys. 29 324 Google Scholar
[15]	Owen L W, Canik J M, Groebner R J, et al. 2010 Nucl. Fusion 50 64017 Google Scholar
[16]	Beurskens M N A, Giudicotti L, Kempenaarsl M, et al. 2008 Re. Scient. Instrum. 79 10.1063
[17]	Candy J, Holland C, Waltz R E, et al. 2009 Phys. Plasmas 16 2137
[18]	Staebler G M, Belli E A, Candy J, Kinsey J E, Dudding H, Patel B 2021 Nuclear Fusion 61 116007 Google Scholar
[19]	Staebler G M, Kinsey J E, Belli E A, et al. 2014 Phys. Plasmas 21 1596
[20]	Belli E A, Candy J, Angioni C 2014 Plasma Phys. Control. Fusion 56 124002 Google Scholar
[21]	Shaing K C, Lai A L 2013 Phys. Plasmas 20 122504 Google Scholar
[22]	Hubbard A E, Boivin R L, Granetz R S, et al. 1998 Phys. Plasmas 5 1744 Google Scholar
[23]	Belli E A, Candy J 2021 Phys. Plasmas 28 062301 Google Scholar
[24]	Staebler G M, Candy J, Belli E A, Kinsey J E, Bonanomi N, Patel B 2021 Plasma Phys. Control. Fusion 63 015013 Google Scholar
[25]	Snyder P B, Groebner R J, Hughes J W, et al. 2011 Nucl. Fusion 51 103016 Google Scholar
[26]	Gao X, Zhang T, Han X, et al. 2015 Nucl. Fusion 55 083015 Google Scholar
[27]	Groebner R J, Baker D R, Burrell K H, et al. 2001 Nucl. Fusion 41 1789 Google Scholar
[28]	Groebner R J, Osborne T H 1998 Phys. Plasmas 5 1800 Google Scholar
[29]	Kinsey J E, Staebler G M, Candy J, et al. 2011 Nucl. Fusion 51 83001 Google Scholar
[30]	McDonald D C, Cordey J G, Thomsen K, 2007 Nucl. Fusion 47 147 Google Scholar
[31]	Saibene G, Sartori R, Loarte A, et al. 2002 Plasma Phys. Control. Fusion 44 1769 Google Scholar

施引文献

图 1 HL-2A高约束模式(H模)放电模拟循环示意图

Fig. 1. Design and analysis of HL-2A high confinement model (H model) discharge integrated simulation workflow.

下载: 全尺寸图片幻灯片

图 2 HL-2A炮号#37012放电参数

Fig. 2. Shot #37012 parameters of HL-2A discharge.

下载: 全尺寸图片幻灯片

图 3 HL-2A托卡马克平衡物理参数实验数据　(a)等离子体中离子温度T_i径向分布; (b)电子温度T_e径向分布; (c)电子密度n_e径向分布

Fig. 3. (a) Radial distribution profile of ion temperature T_i in HL-2A Tokamak plasma; (b) radial distribution profile of electron temperature T_e in HL-2A Tokamak plasma; (c) radial distribution profile of electron density n_e in HL-2A tokamak plasma.

下载: 全尺寸图片幻灯片

图 4 HL-2A 实验数据处理，物理参数拟合径向分布和OMFIT耦合流程

Fig. 4. Flow chart for getting fitting curve processing by using discrete and interpolation of HL-2A experimental data

下载: 全尺寸图片幻灯片

图 5 采用集成模拟程序OMFIT重建的 (a) HL-2A的电子温度T_e和离子温度T_i剖面; (b)电子密度n_e剖面

Fig. 5. Reconstruction of HL-2A parameters by OMFIT integrated simulation code: (a) Electron temperature T_e and ion temperature T_i profiles; (b) electron density n_e profile.

下载: 全尺寸图片幻灯片

图 6 HL-2A托卡马克等离子体电子密度(a)、电子温度(b)、离子温度(c)和旋转角速度(d)随径向剖面的集成模拟和实验拟合结果对比

Fig. 6. HL-2A Tokamak electron density (a), electron temperature(b), ion temperature (c), rotational angular velocity, and (d) versus radial profile by OMFIT and experimental fitting in shot #37012.

下载: 全尺寸图片幻灯片

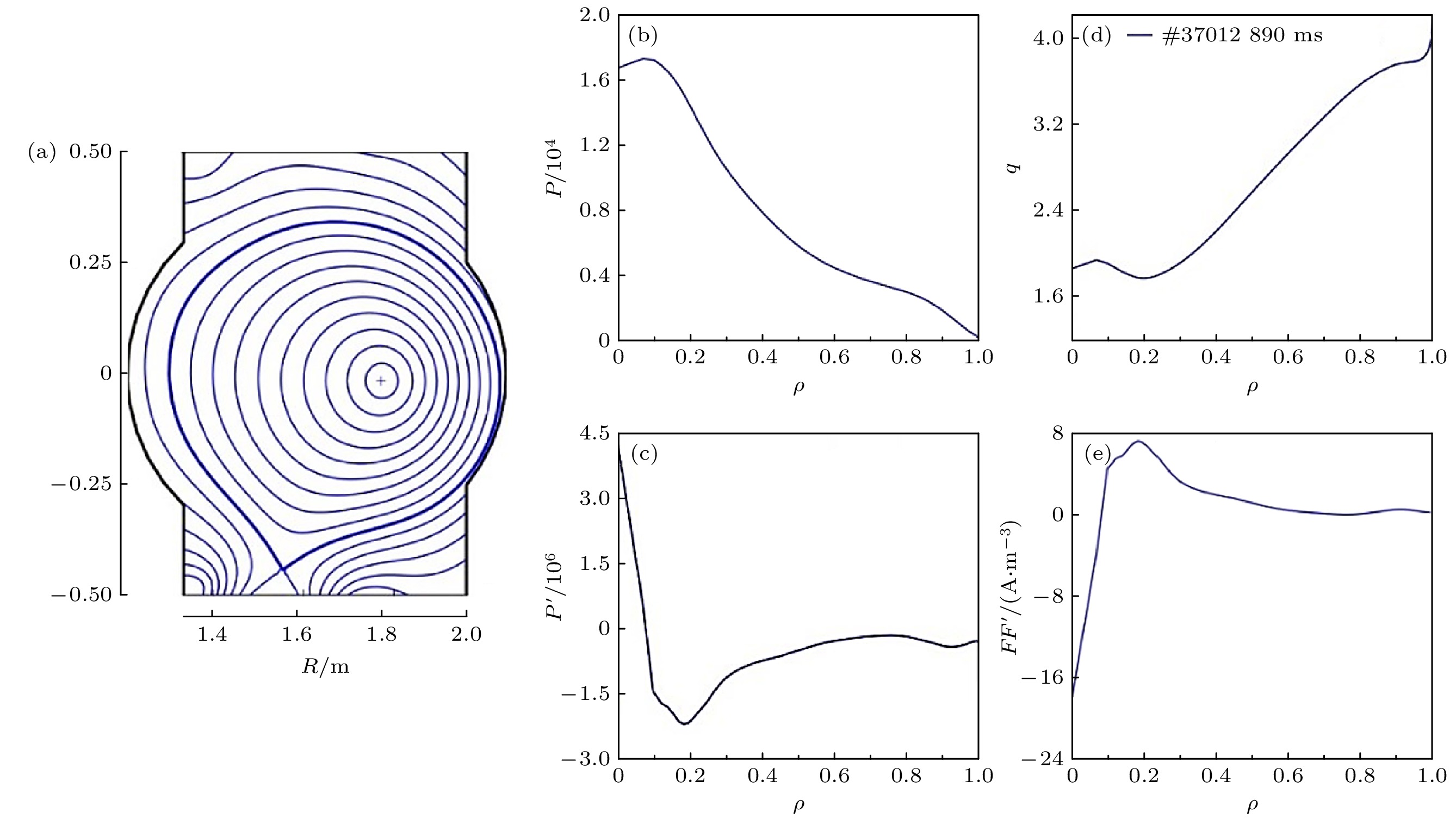
图 7 集成模拟程序OMFIT得到的HL-2A托卡马克等离子体磁场位形结构图 (a); 等离子体压强（单位Pa）径向剖面分布(b); 压强梯度P’（无量纲）径向分布(c); 安全因子q（无量纲）随着径向变化分布剖面(d); 极向电流梯度FF'（A/m³）径向分布剖面(e)

Fig. 7. HL-2A Tokamak plasma magnetic field configuration obtained by integrated simulation code OMFIT (a); pressure profile(unit Pa) (b); profile distribution of the pressure gradient(Dimensionless quantity) (c); profile distribution of safety factor q (Dimensionless quantity) obtained (d); profile distribution of the polar current gradient FF' (unit A/m³)(e).

下载: 全尺寸图片幻灯片

图 8 (a)磁约束托卡马克装置shot #37012由集成模拟程序OMFIT计算的整体电流密度、包含中性束电流密度、自举电流密度、欧姆电流密度和射频电流密度及份额分布曲线; (b)OMFIT程序和平衡反演程序EFIT计算的安全因子q剖面对比图

Fig. 8. (a) Magnetic confinement Tokamak device shot #37012 total current densities calculated by the integrated simulation program OMFIT, including neutral beam current density, bootstrap current density, Ohmic current density, and RF current density with percentages of respective current densities in total current densities; (b) comparison of the safety factor q profiles calculated by the OMFIT program and the balance inversion code EFIT.

下载: 全尺寸图片幻灯片

map

[1]	Wagner F 1982 Phys. Re. Lett. 49 1408 Google Scholar
[2]	李凯 2020 博士学位论文 (合肥: 中国科学技术大学) Li K 2020 Ph. D. Dissertation (Hefei: University of Science and Technology of China) (in Chinese)
[3]	钟武律, 段旭如 2020 原子核物理评论 37 462 Google Scholar Zhong W L, Duan X R 2020 Nucl. Phys. Re. 37 462 Google Scholar
[4]	Snyder P B, Aiba N, Beurskens M 2009 Nucl. Fusion 49 085035 Google Scholar
[5]	Stacey W M, Groebner R J 2003 Phys. Plasm. 10 2412 Google Scholar
[6]	Lao L L, Ferron J R, Groebner R J, et al. 1990 Nucl. Fusion 30 103549
[7]	Fellinger P, Marklein R, Langenberg K J, Klaholz S 1995 Wave Motion 21 47 Google Scholar
[8]	陈文锦, 何小雪, 刘亮, 魏彦玲, 马倩, 余德良 2016 核聚变与等离子体物理 36 104 Google Scholar Chen W J, He X X, Liu L, Wei Y L, Ma Q, Yu D L 2016 Nucl. Fusion Plasma Phys. 36 104 Google Scholar
[9]	Logan N C, Grierson, B A, Haskey S R, Smith S P, Meneghini O, Eldon D 2018 Nucl. Fusion 74 125 Google Scholar
[10]	Meneghini O, Lao L 2013 Plasma Fusion Res. 8 2403009 Google Scholar
[11]	Meneghini O, Smith S P, Lao L L, Izacard O, et al. 2015 Nucl. Fusion 55 083008 Google Scholar
[12]	吴木泉 2020 博士学位论文 (合肥: 中国科学技术大学) Wu M Q 2020 Ph. D. Dissertation (Hefei: University of Science and Technology of China) (in Chinese)
[13]	李强 2009 原子能科学技术 S2 204 Li Q 2009 Atomic Energy Sci. Technol. S2 204 (in Chinese)
[14]	饶军, 陆志鸿, 张劲松等 2009 核聚变与等离子体物理 29 324 Google Scholar Rao J, Lu Z H, Zhang J S, et al. 2009 Nucl. Fusion Plasma Phys. 29 324 Google Scholar
[15]	Owen L W, Canik J M, Groebner R J, et al. 2010 Nucl. Fusion 50 64017 Google Scholar
[16]	Beurskens M N A, Giudicotti L, Kempenaarsl M, et al. 2008 Re. Scient. Instrum. 79 10.1063
[17]	Candy J, Holland C, Waltz R E, et al. 2009 Phys. Plasmas 16 2137
[18]	Staebler G M, Belli E A, Candy J, Kinsey J E, Dudding H, Patel B 2021 Nuclear Fusion 61 116007 Google Scholar
[19]	Staebler G M, Kinsey J E, Belli E A, et al. 2014 Phys. Plasmas 21 1596
[20]	Belli E A, Candy J, Angioni C 2014 Plasma Phys. Control. Fusion 56 124002 Google Scholar
[21]	Shaing K C, Lai A L 2013 Phys. Plasmas 20 122504 Google Scholar
[22]	Hubbard A E, Boivin R L, Granetz R S, et al. 1998 Phys. Plasmas 5 1744 Google Scholar
[23]	Belli E A, Candy J 2021 Phys. Plasmas 28 062301 Google Scholar
[24]	Staebler G M, Candy J, Belli E A, Kinsey J E, Bonanomi N, Patel B 2021 Plasma Phys. Control. Fusion 63 015013 Google Scholar
[25]	Snyder P B, Groebner R J, Hughes J W, et al. 2011 Nucl. Fusion 51 103016 Google Scholar
[26]	Gao X, Zhang T, Han X, et al. 2015 Nucl. Fusion 55 083015 Google Scholar
[27]	Groebner R J, Baker D R, Burrell K H, et al. 2001 Nucl. Fusion 41 1789 Google Scholar
[28]	Groebner R J, Osborne T H 1998 Phys. Plasmas 5 1800 Google Scholar
[29]	Kinsey J E, Staebler G M, Candy J, et al. 2011 Nucl. Fusion 51 83001 Google Scholar
[30]	McDonald D C, Cordey J G, Thomsen K, 2007 Nucl. Fusion 47 147 Google Scholar
[31]	Saibene G, Sartori R, Loarte A, et al. 2002 Plasma Phys. Control. Fusion 44 1769 Google Scholar

[1]	龙婷, 柯锐, 吴婷, 高金明, 才来中, 王占辉, 许敏. HL-2A托卡马克偏滤器脱靶时边缘极向旋转和湍流动量输运. , 2024, 73(8): 088901. doi: 10.7498/aps.73.20231749
[2]	李正吉, 陈伟, 孙爱萍, 于利明, 王卓, 陈佳乐, 许健强, 李继全, 石中兵, 蒋敏, 李永高, 何小雪, 杨曾辰, 李鉴. HL-2A装置高β_N双输运垒实验的集成分析. , 2024, 73(6): 065202. doi: 10.7498/aps.73.20231543
[3]	颜筱宇, 何小斐, 于利明, 刘亮, 陈伟, 石中兵, 卢杰, 魏会领, 韩纪锋, 张轶泼, 钟武律, 许敏. HL-2A装置上成像型中性粒子分析器的物理设计和初步实验结果. , 2023, 72(21): 215212. doi: 10.7498/aps.72.20230768
[4]	施培万, 朱霄龙, 陈伟, 余鑫, 杨曾辰, 何小雪, 王正汹. HL-2A装置上电子回旋共振加热沉积位置影响鱼骨模主动控制效果的实验研究. , 2023, 72(21): 215208. doi: 10.7498/aps.72.20230696
[5]	侯玉梅, 陈伟, 邹云鹏, 于利明, 石中兵, 段旭如. HL-2A装置高能量离子驱动的比压阿尔芬本征模的扫频行为. , 2023, 72(21): 215211. doi: 10.7498/aps.72.20230726
[6]	孙梓源, 王元震, 刘悦. 预测HL-2A托卡马克台基结构的MHD稳定性数值研究. , 2022, 71(22): 225201. doi: 10.7498/aps.71.20221098
[7]	罗一鸣, 王占辉, 陈佳乐, 吴雪科, 付彩龙, 何小雪, 刘亮, 杨曾辰, 李永高, 高金明, 杜华荣, 昆仑集成模拟设计组. HL-2A上NBI加热H模实验的集成模拟分析. , 2022, 71(7): 075201. doi: 10.7498/aps.71.20211941
[8]	陈撷宇, 牟茂淋, 苏春燕, 陈少永, 唐昌建. HL-2A中环向旋转影响等离子体对共振磁扰动的响应过程. , 2020, 69(19): 195201. doi: 10.7498/aps.69.20200519
[9]	李安梁, 蔡洪, 张士峰, 白锡斌. 浮球式惯导平台悬浮稳定问题的动力学建模与控制. , 2013, 62(15): 150203. doi: 10.7498/aps.62.150203
[10]	冯北滨, 姚良骅, 陈程远, 季小全, 钟武律, 石中兵, 余德良, 崔正英, 宋显明, 段旭如. HL-2A装置上超声分子束注入触发L-H转换的实验研究. , 2013, 62(1): 015203. doi: 10.7498/aps.62.015203
[11]	刘春华, 聂林, 黄渊, 季小全, 余德良, 刘仪, 冯震, 姚可, 崔正英, 严龙文, 丁玄同, 董家齐, 段旭如. HL-2A托卡马克上的边缘局域模特性初步研究. , 2012, 61(20): 205201. doi: 10.7498/aps.61.205201
[12]	郑灵, 赵青, 周艳. HL-2A第一镜挡板防护效果模拟. , 2011, 60(8): 085204. doi: 10.7498/aps.60.085204
[13]	钟武律, 段旭如, 余德良, 韩晓玉, 杨立梅. HL-2A托卡马克中性束辐射光谱的数值模拟. , 2010, 59(5): 3336-3343. doi: 10.7498/aps.59.3336
[14]	姚良骅, 冯北滨, 陈程远, 冯震, 李伟, 焦一鸣. 中国环流器二号A(HL-2A)超声分子束注入最新结果. , 2008, 57(7): 4159-4165. doi: 10.7498/aps.57.4159
[15]	洪文玉, 严龙文, 赵开君, 兰涛, 董家齐, 俞昌旋, 程均, 钱俊, 刘阿棣, 罗萃文, 徐征宇, 黄渊, 杨青巍. HL-2A装置中的带状流三维特性研究和探针设计. , 2008, 57(2): 962-968. doi: 10.7498/aps.57.962
[16]	石中兵, 姚良骅, 丁玄同, 段旭如, 冯北滨, 刘泽田, 肖维文, 孙红娟, 李旭, 李伟, 陈程远, 焦一鸣. HL-2A托卡马克超声分子束注入深度和加料效果研究. , 2007, 56(8): 4771-4777. doi: 10.7498/aps.56.4771
[17]	游天雪, 袁保山, 李芳著. 用可移动电流丝方法重建HL-2A等离子体边界的研究. , 2007, 56(9): 5323-5329. doi: 10.7498/aps.56.5323
[18]	郑银甲, 黄渊, 冯震, 施乐, 崔成和, 王明旭, 徐红兵. HL-2A托卡马克送气成像研究. , 2007, 56(3): 1452-1460. doi: 10.7498/aps.56.1452
[19]	袁保山, 游天雪, 秦运文, 冯北滨, 季小全. HL-2A等离子体约束参数的实时确定. , 2006, 55(3): 1315-1319. doi: 10.7498/aps.55.1315
[20]	袁保山, 游天雪, 刘莉, 李芳著, 杨青巍, 冯北滨. HL-2A等离子体形状实时显示系统. , 2006, 55(5): 2403-2408. doi: 10.7498/aps.55.2403

计量

文章访问数: 5308
PDF下载量: 102
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

HL-2A高约束先进运行模式等离子体电流剖面集成模拟