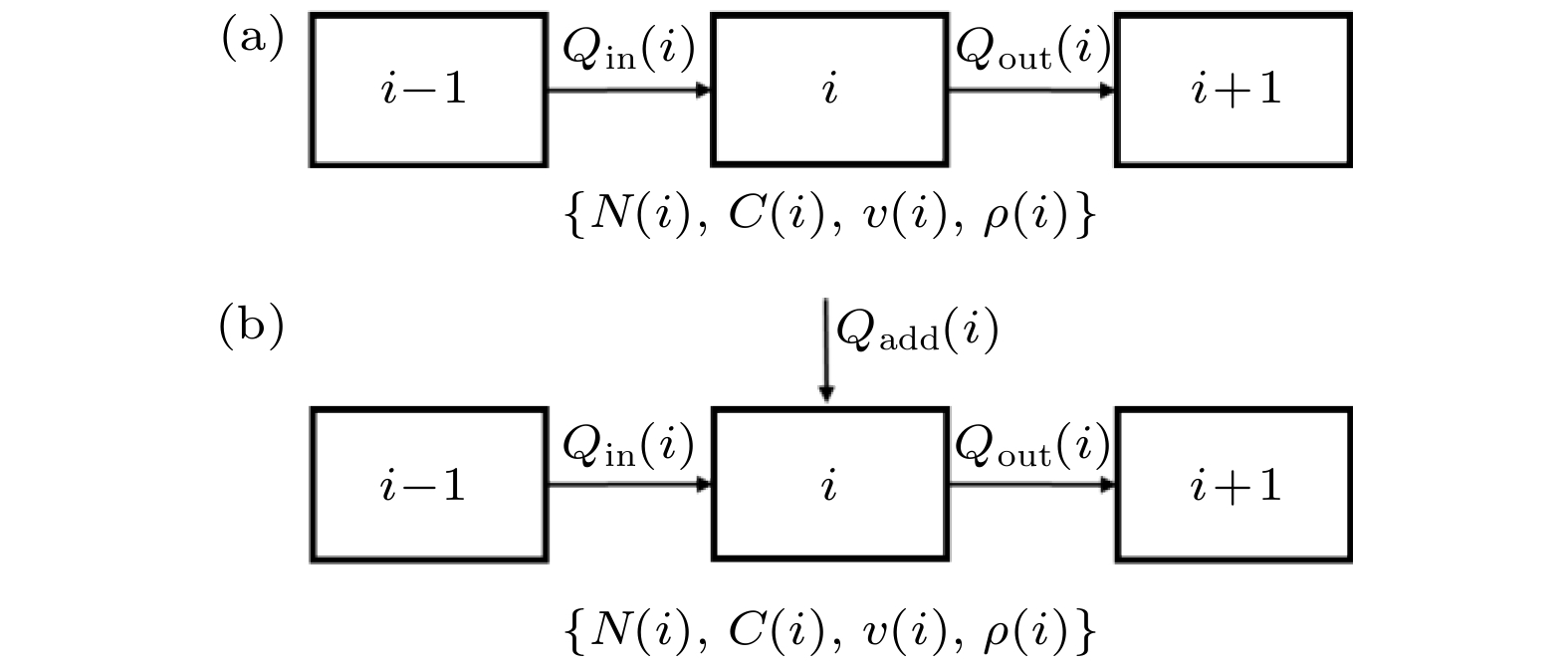
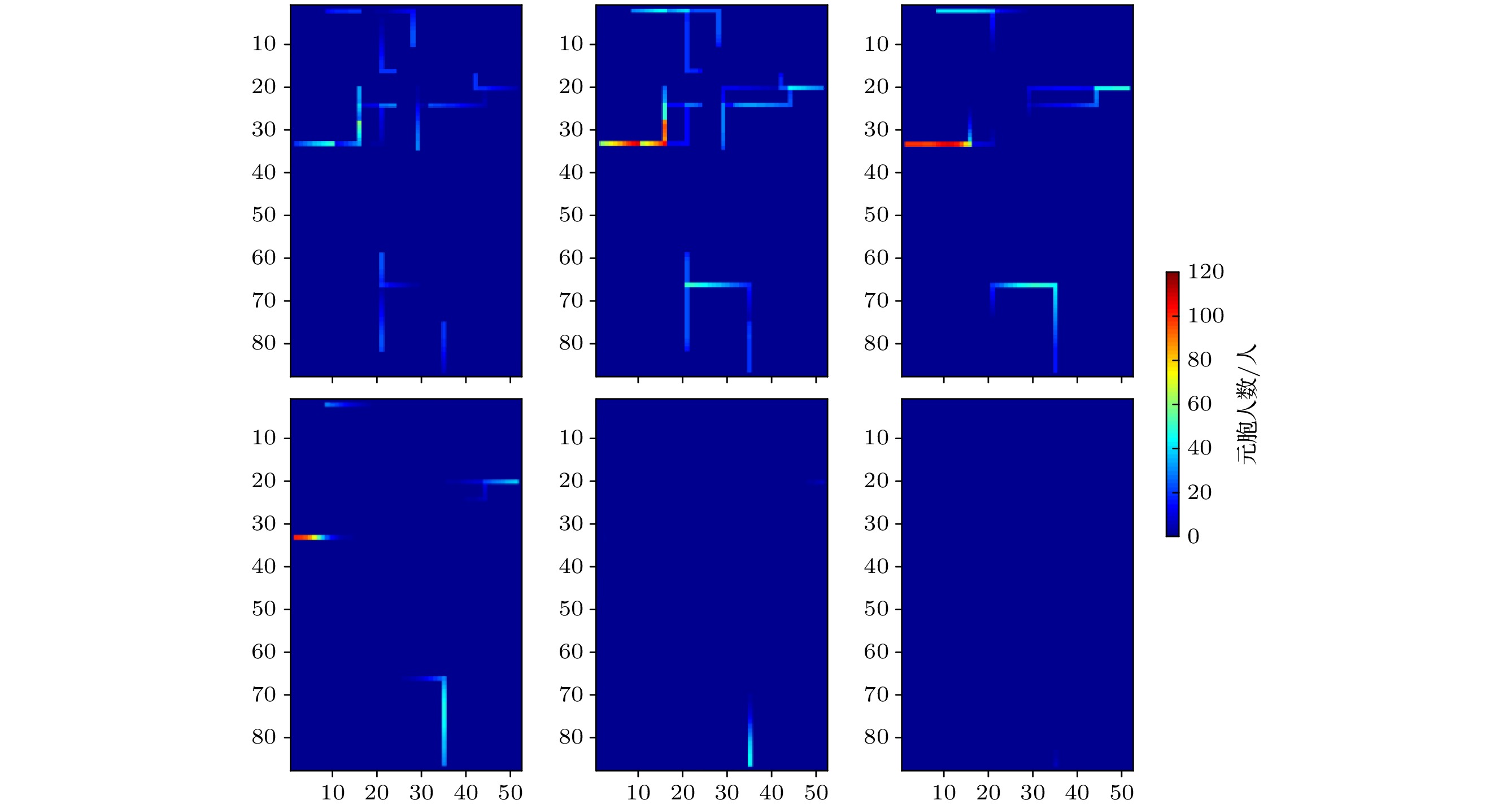
-
传统元胞自动机疏散模型中, 空间多划分为微观层面的精细网格, 难以对大范围的疏散场景进行模拟. 基于此, 本文结合行人流的运动特征, 建立了应用于大尺度人员疏散场景的人员疏散介观元胞自动机模型. 该模型以道路元胞划分替代平面网格元胞划分方式, 并引入“源加载”元胞加载模拟场景内疏散人员, 建立元胞间状态转移方程模拟疏散过程中的人员运动. 应用该模型, 对高校校园进行疏散子网划分, 模拟应急疏散过程并规划疏散路径, 既可以对场景内宏观疏散情况进行分析, 又可以观测单个元胞的状态变化. 基于模拟结果, 能够发现实际疏散过程中可能存在的问题, 提出相应的改进指引和意见.In the traditional cellular automata evacuation model, the space is divided into fine grids at a micro level, which is mainly used in a two-dimensional plane case. The evacuation space is mostly a small-scale architectural space or local area. Therefore, it is difficult to simulate a wide range of evacuation scenario, and there are less researches of the cellular automata model for a wide range of evacuation. Therefore, this article combines the movement characteristics and status of the pedestrian flow to establish a mesoscopic cellular automata model of evacuation applied to larger evacuation scenarios. This model uses road cell division instead of planar grid cell division, which augments the area of a single cell physically, increases the number of people occupied by a single cell, and expresses the number of people in each cell in the form of state variables. By changing personnel density and personnel speed, and by introducing “source loading” cell loading to simulate the evacuation of people in the scene, the behavior of pedestrians evacuating from the building to the road in the actual evacuation process can be simulated. The state transition equation simulates the movement of people in the evacuation process. When the number of people in the cell is larger, the density of people in the cell is higher, and their walking speed also decreases, which reflects the distribution and movement characteristics of pedestrian flow. This paper uses this model to divide the evacuation area of the college campus, and divides the entire campus into four evacuation areas. The evacuees in each area are evacuated corresponding to the corresponding exit, by planning the evacuation path, pedestrians walking from the “source loading” cell to the exit for evacuation. Through simulation, it is possible to analyze the macro-evacuation situation in the scene and observe the status change of a single cell. There are observed a high density of people in local road sections during campus evacuation, and the problem about the distribution of people on campus problems such as unevenness of pedestrian distribution and long evacuation schedules in certain places. Through the simulation of this model, possible problems in the actual evacuation process are found, and the improvement guidance and opinions are presented correspondingly.
-
Keywords:
- mesoscopic cellular automata /
- large-scale simulation /
- pedestrian evacuation /
- partition evacuation
[1] Miyagawa D, Ichinose G 2020 Physica A 549 124376
Google Scholar
[2] Ji J W, Lu L G, Jin Z H, Wei S P, Ni L 2018 Physica A 509 1034
Google Scholar
[3] Maniccam S 2003 Physica A 321 653
Google Scholar
[4] Leng B, Wang J Y, Zhao W Y, Xiong Z 2014 Physica A 402 119
Google Scholar
[5] Jooyoung K, Chiwon A, Seungjae L 2018 Physica A 510 507
Google Scholar
[6] Hanisch A, Tolujew J, Richter K 2003 Proc. Winter Simul. Conf. 2 1635
[7] Crociani L, Lämmel G, Park H J, Vizzari G 2017 Transportation Research Board. Annual Meeting of the Transportation Research Board Washington, D.C., USA, Jan, 2017 p1
[8] Lämmel G, Flötteröd G 2015 Proc. Comput. Sci 52 950
Google Scholar
[9] Kaji M, Inohara T 2017 Physica A 467 85
Google Scholar
[10] Shi M, Lee E W M, Ma Y 2018 Physica A 497 198
Google Scholar
[11] 胡俊, 游磊 2014 63 080507
Google Scholar
Hu J, You L 2014 Acta Phys. Sin. 63 080507
Google Scholar
[12] Hu J, You L, Wei J, Gu M S, Liang Y 2014 Phys. Lett. A 378 1913
Google Scholar
[13] 张磊, 岳昊, 李梅, 王帅, 米雪玉 2015 64 060505
Zhang L, Yue H, Li M, Wang S, Mi X Y 2015 Acta Phys. Sin. 64 060505
[14] 任刚, 陆丽丽, 王炜 2012 61 144501
Google Scholar
Ren G, Lu L L, Wang W 2012 Acta Phys. Sin. 61 144501
Google Scholar
[15] 胥旋, 史聪灵, 李建, 车洪磊 2018 中国安全生产科学技术 14 20
Xu X, Shi C L, Li J, Che H L 2018 J. Saf. Sci. Technol. 14 20
[16] 金泽人, 阮欣, 李越 2018 同济大学学报(自然科学版) 46 1026
Google Scholar
Jin Z R, Ruan X, Li Y 2018 J. Tongji Univ. (Nat. Sci.) 46 1026
Google Scholar
[17] 陆卓谟, 秦文虎 2011 东南大学学报(自然科学版) 41 1295
Google Scholar
Lu Z M, Qin W H 2011 J. Southeast Univ. (Nat. Sci. Ed.) 41 1295
Google Scholar
[18] 张维, 郑小平, 程礼盛 2013 电子科技大学学报(社科版) 15 26
Zhang W, Zheng X P, Cheng L S 2013 J. Univ. Electron. Sci. Technol. Chin. (Social Sci. Ed.) 15 26
[19] Cao S C, Song W G, Lü W, Fang Z M 2015 Physica A 436 45
Google Scholar
[20] 陈雍容 2012 博士学位论文 (武汉: 华中科技大学)
Chen Y R 2012 Ph. D. Dissertation (Wuhan: Huazhong University of Science and Technology) (in Chinese)
[21] 杨兆升, 高学英, 孙迪 2011 交通运输工程学报 11 114
Google Scholar
Yang Z S, Gao X Y, Sun D 2011 J. Traff. Transp. Eng. 11 114
Google Scholar
[22] Muramatsu M, Irie T, Nagatani T 1999 Physica A 267 487
Google Scholar
[23] Burstedde C, Klauck K, Schadschneider A, Zittartz J 2001 Physica A 295 507
Google Scholar
[24] 于彦飞 2008 博士学位论文 (合肥: 中国科学技术大学)
Yu Y F 2008 Ph. D. Disseration (Hefei: University of Science and Technology of China) (in Chinese)
[25] Xu X, Song W G, Zheng H Y 2008 Physica A 387 5567
Google Scholar
[26] Ma J, Song W G, Zhang J, Lo S M, Liao G X 2010 Physica A 389 2101
Google Scholar
-
图 4 疏散道路元胞间宏观状态量更新规则示意图 (a) 无加载源; (b) 有加载源
Fig. 4. The update rule of macro-state variable between the evacuation road cells: (a) Without load source; (b) with load source.
图 8 “源加载”元胞加载概率密度分布图
Fig. 8. Probability density distribution figure of “source loading”cell.
图 9 各出口及总疏散人数随时间变化关系
Fig. 9. The relationship between the exits and the total number of evacuees varies with time.
图 10 各出口及总疏散剩余人数随时间变化关系
Fig. 10. The total number of remaining evacuees at each exit varies with time.
图 13 各“观测”元胞速度随时间的变化情况
Fig. 13. Variations of cell velocity with time in each observed cell.
图 14 空间人员数量分布图 (a) t = 100 s; (b) t = 200 s; (c) t = 300 s; (d) t = 400 s; (e) t = 500 s; (f) t = 600 s
Fig. 14. Spatial staffing distributions: (a) t = 100 s; (b) t = 200 s; (c) t = 300 s; (d) t = 400 s; (e) t = 500 s; (f) t = 600 s.
表 1 区域道路元胞编码统计信息
Table 1. Statistical information of regional road cellular coding.
道路
编号长/m 宽/m 元胞
数量“源加载”元胞 “出口”元胞 1 280 12 28 Cell1,8 Cell1,1 2 290 6 29 Cell2,9,
Cell2,29— 3 230 6 23 — Cell3,23 4 290 6 29 Cell4,9,
Cell4,17— 5 200 6 20 Cell5,9 Cell5,1 6 90 6 9 — — 7 68 6 7 — — 8 250 6 25 — — 9 180 6 18 Cell9,5,
Cell9,13— 10 795 6 80 Cell10,59,
Cell10,80— 11 90 6 9 Cell11,9 — 12 148 6 15 — — 13 530 6 53 Cell13,21 — 14 70 6 7 — — 15 326 6 33 Cell15,22 Cell15,33 
下载: 导出CSV
表 2 模型参数
Table 2. Model parameters.
参数 含义 值 l 道路元胞长度 10 m w 道路元胞宽度 6 m vf 自由疏散速度 1.5 m/s $\Delta t$ 计算时间间隔 1 s ρm 拥塞临界密度 5 per/m2
下载: 导出CSV
表 3 各“源加载”元胞加载人数
Table 3. The number of pedestrians loaded by each ‘source loading’ cell.
“源加载”
元胞加载总
人数/人“源加载”
元胞加载总
人数/人Cell1, 8 500 Cell2, 9 500 Cell2, 29 500 Cell4, 9 700 Cell4, 17 500 Cell5, 9 900 Cell9, 5 800 Cell9, 13 800 Cell10, 59 600 Cell10, 80 600 Cell11, 9 600 Cell13, 21 700 Cell15, 22 500
下载: 导出CSV
表 4 各出口疏散人数
Table 4. Evacuation number at each exit.
出口 疏散总人数/人 出口1 1600 出口2 1700 出口3 3200 出口4 1700 总计 8200
下载: 导出CSV
-
[1] Miyagawa D, Ichinose G 2020 Physica A 549 124376
Google Scholar
[2] Ji J W, Lu L G, Jin Z H, Wei S P, Ni L 2018 Physica A 509 1034
Google Scholar
[3] Maniccam S 2003 Physica A 321 653
Google Scholar
[4] Leng B, Wang J Y, Zhao W Y, Xiong Z 2014 Physica A 402 119
Google Scholar
[5] Jooyoung K, Chiwon A, Seungjae L 2018 Physica A 510 507
Google Scholar
[6] Hanisch A, Tolujew J, Richter K 2003 Proc. Winter Simul. Conf. 2 1635
[7] Crociani L, Lämmel G, Park H J, Vizzari G 2017 Transportation Research Board. Annual Meeting of the Transportation Research Board Washington, D.C., USA, Jan, 2017 p1
[8] Lämmel G, Flötteröd G 2015 Proc. Comput. Sci 52 950
Google Scholar
[9] Kaji M, Inohara T 2017 Physica A 467 85
Google Scholar
[10] Shi M, Lee E W M, Ma Y 2018 Physica A 497 198
Google Scholar
[11] 胡俊, 游磊 2014 63 080507
Google Scholar
Hu J, You L 2014 Acta Phys. Sin. 63 080507
Google Scholar
[12] Hu J, You L, Wei J, Gu M S, Liang Y 2014 Phys. Lett. A 378 1913
Google Scholar
[13] 张磊, 岳昊, 李梅, 王帅, 米雪玉 2015 64 060505
Zhang L, Yue H, Li M, Wang S, Mi X Y 2015 Acta Phys. Sin. 64 060505
[14] 任刚, 陆丽丽, 王炜 2012 61 144501
Google Scholar
Ren G, Lu L L, Wang W 2012 Acta Phys. Sin. 61 144501
Google Scholar
[15] 胥旋, 史聪灵, 李建, 车洪磊 2018 中国安全生产科学技术 14 20
Xu X, Shi C L, Li J, Che H L 2018 J. Saf. Sci. Technol. 14 20
[16] 金泽人, 阮欣, 李越 2018 同济大学学报(自然科学版) 46 1026
Google Scholar
Jin Z R, Ruan X, Li Y 2018 J. Tongji Univ. (Nat. Sci.) 46 1026
Google Scholar
[17] 陆卓谟, 秦文虎 2011 东南大学学报(自然科学版) 41 1295
Google Scholar
Lu Z M, Qin W H 2011 J. Southeast Univ. (Nat. Sci. Ed.) 41 1295
Google Scholar
[18] 张维, 郑小平, 程礼盛 2013 电子科技大学学报(社科版) 15 26
Zhang W, Zheng X P, Cheng L S 2013 J. Univ. Electron. Sci. Technol. Chin. (Social Sci. Ed.) 15 26
[19] Cao S C, Song W G, Lü W, Fang Z M 2015 Physica A 436 45
Google Scholar
[20] 陈雍容 2012 博士学位论文 (武汉: 华中科技大学)
Chen Y R 2012 Ph. D. Dissertation (Wuhan: Huazhong University of Science and Technology) (in Chinese)
[21] 杨兆升, 高学英, 孙迪 2011 交通运输工程学报 11 114
Google Scholar
Yang Z S, Gao X Y, Sun D 2011 J. Traff. Transp. Eng. 11 114
Google Scholar
[22] Muramatsu M, Irie T, Nagatani T 1999 Physica A 267 487
Google Scholar
[23] Burstedde C, Klauck K, Schadschneider A, Zittartz J 2001 Physica A 295 507
Google Scholar
[24] 于彦飞 2008 博士学位论文 (合肥: 中国科学技术大学)
Yu Y F 2008 Ph. D. Disseration (Hefei: University of Science and Technology of China) (in Chinese)
[25] Xu X, Song W G, Zheng H Y 2008 Physica A 387 5567
Google Scholar
[26] Ma J, Song W G, Zhang J, Lo S M, Liao G X 2010 Physica A 389 2101
Google Scholar
下载:
计量
- 文章访问数: 5447
- PDF下载量: 111
- 被引次数: 0
