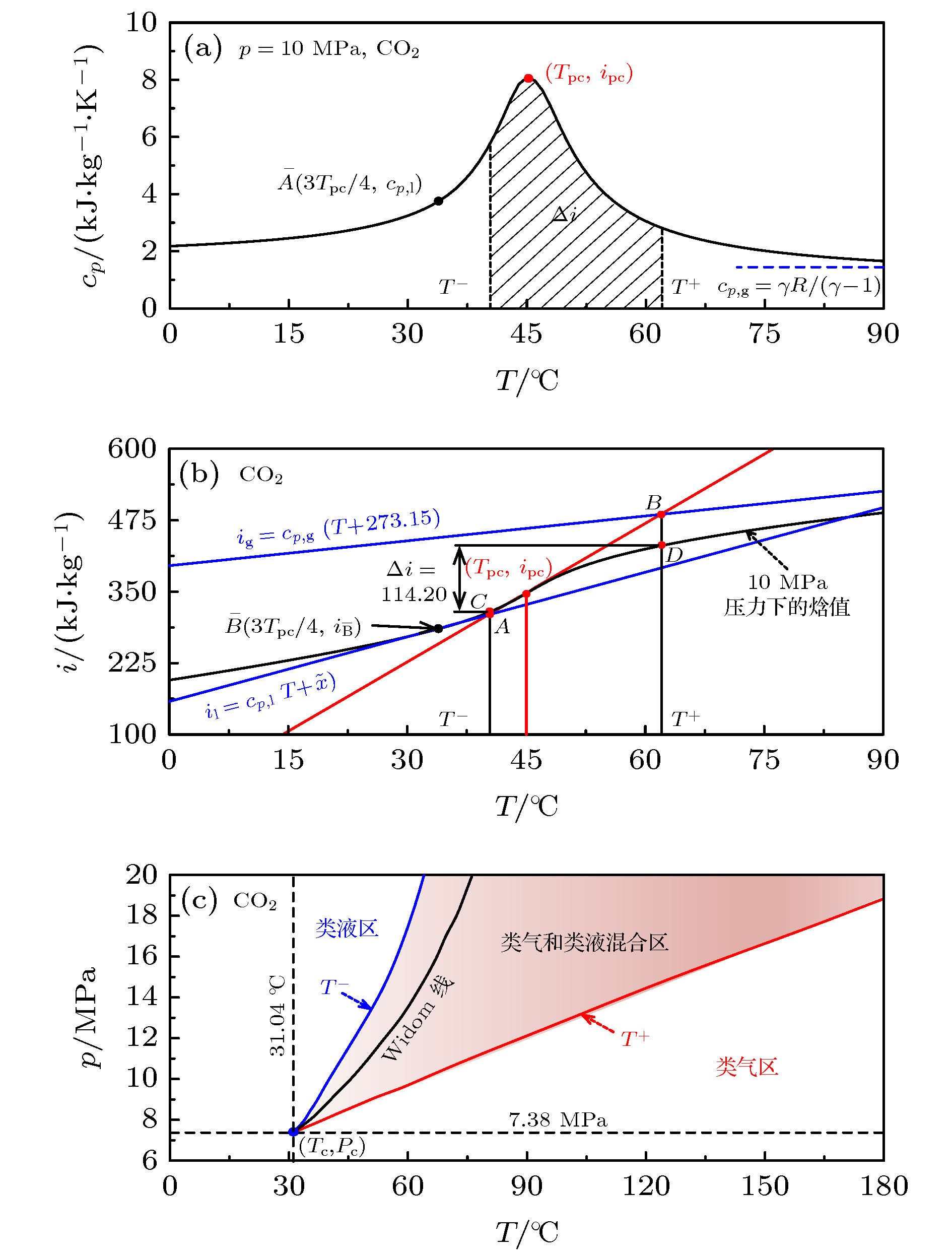
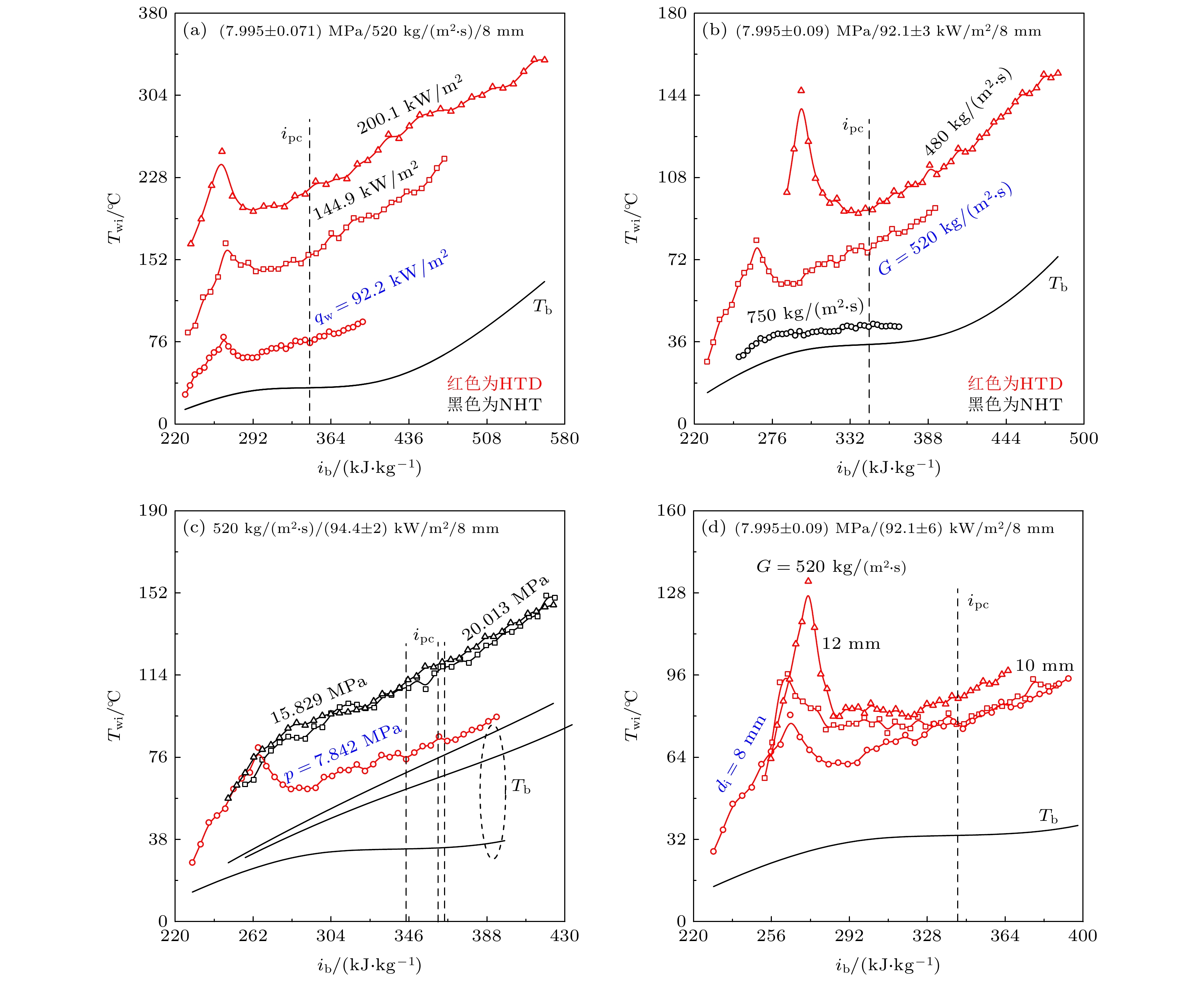
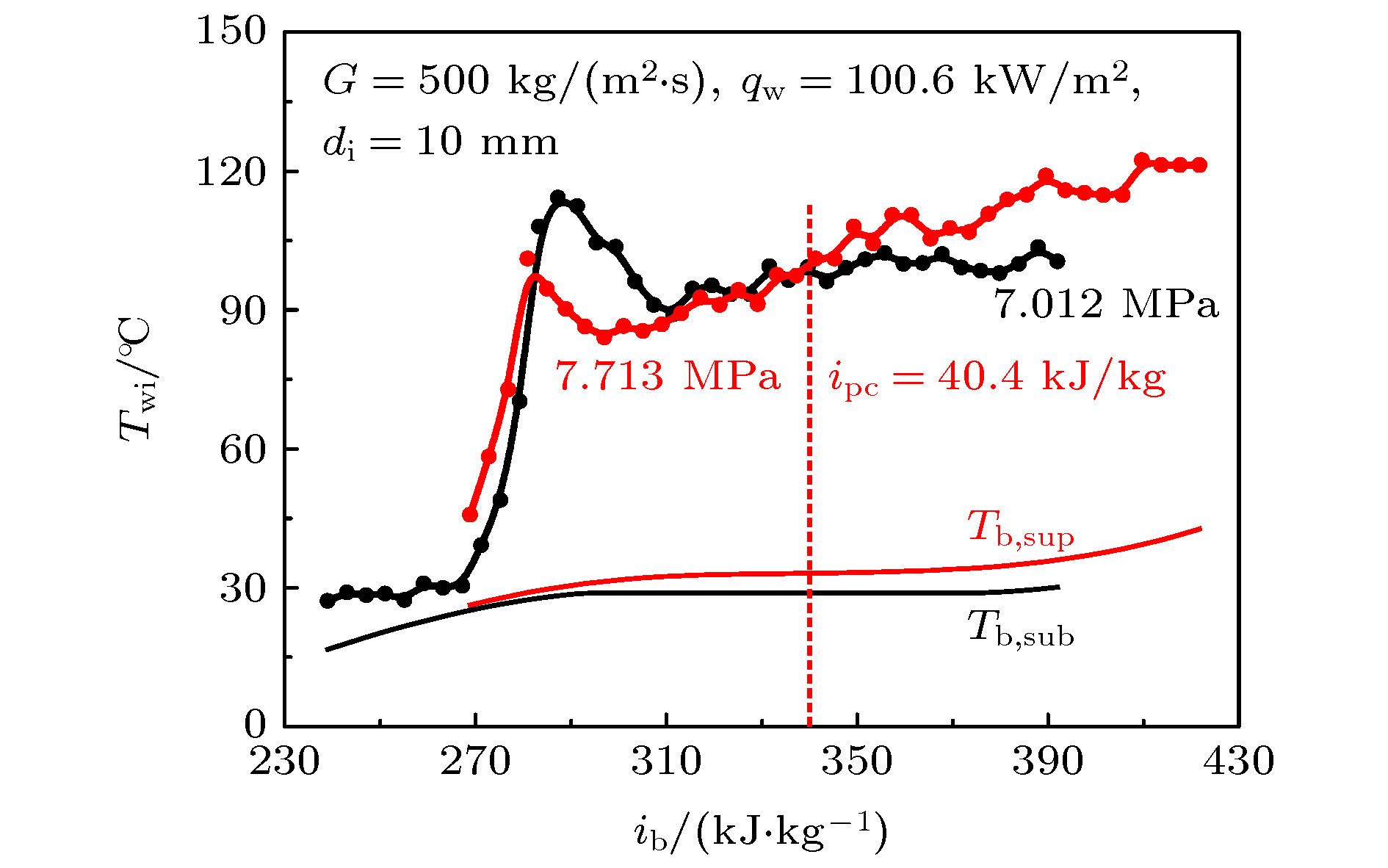
-
超临界流体广泛应用于工程技术领域, 其流动传热特性对工程设计具有重要意义, 但是, 由于超临界流体的物理微观和宏观行为的机理尚不清晰, 所以其异常的流动传热特性并未得到很好的解决. 普遍认为超临界流体在分子尺度上可分为类气和类液两种不同的特性, 直到最近通过实验在宏观上监测到超临界水类液和类气之间的转变, 且这一过程与拟沸腾理论一致, 使得问题逐渐变得清晰. 本文基于拟沸腾理论对超临界CO2异常流动传热行为进行了研究, 在假设类液和类气转换过程不均匀的情况下, 从经典的量纲分析和亚临界过冷沸腾理论模型出发, 提出了一个适用于超临界流体拟沸腾换热过程的分析方法. 通过引入表征类气膜生长速度与流体主流平均流速之比π = (qw·ρl)/(G·Δi·ρg)和表征近壁区类气膜温度梯度π13 = (qw·βpc·di)/λg两个无量纲数, 来表征拟沸腾如何导致传热恶化, 解释了超临界CO2竖直向上加热流动过程中的异常换热特性, 即较大的类气膜生长速度使近壁区快速聚集了较多的高温流体, 而较大的类气膜温度梯度使类气膜覆盖在壁面. 当核心的冷类液不能充分润湿热壁面时, 传热恶化. 新无量纲数较好的诠释了超临界流体拟沸腾诱导传热恶化机制, 为超临界拟沸腾传热研究提供了理论依据.Supercritical fluids are widely used in engineering technology, and the flow and heat transfer characteristics are very important for engineering design. However, due to the fact that the physical micro- and macroscopic behaviors of supercritical fluids are still open, neither the heat transfer mechanism nor the flow mechanism of supercritical fluids has been well revealed. It is widely believed that liquid-like (LL) and gas-like (GL) supercritical fluid are two phases distinguishable on a molecular scale. Only recently, has it become clear that the macroscopic transition from LL to GL supercritical state, when crossing the Widomline, is successfully detected in experiment, and explained based on the pseudo-boiling concept. In this paper, the abnormal flow and heat transfer behavior of supercritical CO2 are studied based on the pseudo-boiling theory. On the assumption that the transition from LL to GL is heterogeneous, an analysis method for pseudo-boiling heat transfer is developed from classical dimensional analysis and subcritical subcooled boiling theory of models. To analyze the pseudo-boiling resulting in heat transfer deterioration process of supercritical fluid, two dimensionless numbers which are π = (qw·ρl)/(G·Δi·ρg) and π13 = (qw·βpc·di)/λg are proposed to explain the anomalous heat transfer characteristics in vertical upward heating flow. The former π reflects the rate of conversion between gas-like and liquid-like fluid. The larger gas-like conversion rate promotes the rapid production of more high-temperature fluid in the near-wall region, and the latter π13 characterizes the temperature gradient of gas-like film near the wall: the larger temperature gradient causes the gas film to cover the wall surface. The heat transfer deterioration may occur when the cooler liquid-like fluid of the core region cannot rewet the hot wall adequately. The new dimensionless numbers can successfully explain the heat transfer deterioration of supercritical fluid flow induced by pseudo-boiling. Our work paves the way to understanding the heat transfer and flow for supercritical fluids which establishes a relation among the internal flow, heat transfer field characteristics, boundary conditions and physical properties based on the pseudo-boiling theory preliminarily. The results of dimensional analysis can be applied to the similarity theory analysis of different fluids, which is of significance for promoting the theoretical research of supercritical fluid heat transfer on the basis of pseudo-boiling concept.
-
Keywords:
- supercritical carbon dioxide /
- pseudo-boiling /
- heat transfer deterioration /
- dimensional analysis
[1] Tsai W C, Wang Y 2019 Prog. Polym. Sci. 98 101161
Google Scholar
[2] Knez Z, Markocic E 2014 Energy 77 235
Google Scholar
[3] Pizzarelli M 2018 Int. Commun. Heat Mass Transf. 95 132
Google Scholar
[4] Wang H, Leungc L K H, Wang W S, Bi Q C 2018 Appl. Therm. Eng. 142 573
Google Scholar
[5] Knapp K K, Sabersky R H 1966 Int. J. Heat Mass Transf. 9 41
Google Scholar
[6] Ackerman J W 1970 J. of Heat Transfer 92 490
Google Scholar
[7] Stewart E, Stewart P, Watson A 1973 Int. J. Heat Mass Transfer 16 257
Google Scholar
[8] Ambrosini W 2007 Nucl. Eng. Des. 237 1164
Google Scholar
[9] Ma T, Wang S H 2011 AIP Advances 1 042101
Google Scholar
[10] Simeoni G G, Bryk T, Gorelli F A, Krisch M, Ruocco G, Santoro M, Scopigno T 2010 Nat. Phys. 6 503
Google Scholar
[11] Ha M Y, Yoon T J, Tlusty T, Jho Y, Lee W B 2018 J. Phys. Chem. Lett. 9 1734
Google Scholar
[12] Banuti D T 2015 J. Supercrit. Fluids 98 12
Google Scholar
[13] Maxim F, Contescu C, Boillat P, Niceno B, Karalis K, Testino A, Ludwig C 2019 Nat. Commun. 10 1
Google Scholar
[14] Zhu B G, Xu J L, Wu X M, Xie J, Li M J 2019 J Int. J. Therm. Sci. 136 254
Google Scholar
[15] Xu J L, Zhang H S, Zhu B G, Xie J 2020 Sol. Energy 195 27
Google Scholar
[16] 张海松, 朱鑫杰, 朱兵国, 徐进良, 刘欢 2020 6 064401
Google Scholar
Zhang H S, Zhu X J, Zhu B G, Xu J L, Liu H 2020 Acta Phys. Sin. 6 064401
Google Scholar
[17] Yildiz S, Groeneveld D C 2014 Int. Commun. Heat Mass Transf. 54 27
Google Scholar
[18] 张思宇 2015 博士学位论文 (上海: 上海交通大学)
Zhang S Y 2015 Ph. D. Dissertation(Shanghai: Shanghai Jiaotong University) (in Chinese)
[19] Kang K H, Chang S H 2009 Int. J. Heat Mass Transfer 52 4946
Google Scholar
[20] Yamashita T, Yoshida S, Mori H, Morooka S, Komita H 2003 GENES4/ANP2003, Kyoto, Japan., Sep. 15–19, 2003 1119
[21] Lei X L, Li H X, Zhang W Q, Dinh N T, Guo Y M, Yu S Q 2017 Appl. Therm. Eng. 113 609
Google Scholar
[22] Shen Z, Yang D, Chen G M, Xiao F 2014 Int. J. Heat Mass Transfer 68 669
Google Scholar
[23] Buckingham E 1914 Phys. Rev. 4 345
[24] 罗峰, 胥蕊娜, 姜培学 2014 工程热 6 1170
Luo F, Xu R N, Jiang P X 2014 J. Eng. Thermophysics 6 1170
[25] 刘生晖, 黄彦平, 刘光旭, 王俊峰, 王金宇 2019 核动力工程 40 18
Google Scholar
Liu S H, Huang Y P, Liu G X, Wang J F, Wang J Y 2019 Nucl. Power Engineering 40 18
Google Scholar
[26] 廖长江, 李会雄 2015 工程热 1 111
Liao C J, Li H X 2015 J. Eng. Thermophysics 1 111
-
图 1 不同压力下的SCF穿越WL的物性变化
Fig. 1. The physical properties of SCF crossing WL under different pressures.
图 2 不同压力下的CO2密度随温度变化分布
Fig. 2. Density of CO2 varies with temperature under different pressures.
图 3 超临界CO2拟沸腾相变焓Δi定义和跨越温差ΔT
Fig. 3. Defining pseudo-boiling enthalpy Δi and temperature span ΔT of S-CO2 during pseudo-boiling.
图 4 不同参数下CO2内壁温随焓值变化分布
Fig. 4. The inner wall temperature distribution of S-CO2 with enthalpy under varies parameters.
图 5 亚临界DNB (黑色)和超临界压力下传热恶化壁温(红色)分布对比
Fig. 5. Comparison of wall temperature distribution subcritical DNB (black) and supercritical heat transfer deterioration (red).
图 6 不同超临界流体在正常传热和恶化传热过程中的Twi/Tpc和Tb/Tpc随焓值变化分布
Fig. 6. Distribution of Twi/Tpc and Tb/Tpc with enthalpy during normal heat transfer (NHT) and heat transfer deterioration(HTD)of different supercritical fluids.
图 7 正常和恶化传热下类气膜内的温度梯度和内壁温随焓值分布
Fig. 7. Distribution of temperature gradients and inner wall temperature with enthalpy in gas-like film under normal heat transfer(NHT) and heat transfer deterioration(HTD).
图 8 正常传热和恶化传热下的新无量纲数π、内壁温Twi和换热系数h随焓值分布
Fig. 8. Distribution of the new dimensionless numberπ, inner wall temperature Twi and heat transfer coefficient h with enthalpy under normal heat transfer (NHT) and deteriorated heat transfer (HTD).
图 9 新无量纲数作用超临界流体拟沸腾传热恶化机制
Fig. 9. New dimensionless action on number deterioration of pseudo-boiling heat transfer mechanism.
-
[1] Tsai W C, Wang Y 2019 Prog. Polym. Sci. 98 101161
Google Scholar
[2] Knez Z, Markocic E 2014 Energy 77 235
Google Scholar
[3] Pizzarelli M 2018 Int. Commun. Heat Mass Transf. 95 132
Google Scholar
[4] Wang H, Leungc L K H, Wang W S, Bi Q C 2018 Appl. Therm. Eng. 142 573
Google Scholar
[5] Knapp K K, Sabersky R H 1966 Int. J. Heat Mass Transf. 9 41
Google Scholar
[6] Ackerman J W 1970 J. of Heat Transfer 92 490
Google Scholar
[7] Stewart E, Stewart P, Watson A 1973 Int. J. Heat Mass Transfer 16 257
Google Scholar
[8] Ambrosini W 2007 Nucl. Eng. Des. 237 1164
Google Scholar
[9] Ma T, Wang S H 2011 AIP Advances 1 042101
Google Scholar
[10] Simeoni G G, Bryk T, Gorelli F A, Krisch M, Ruocco G, Santoro M, Scopigno T 2010 Nat. Phys. 6 503
Google Scholar
[11] Ha M Y, Yoon T J, Tlusty T, Jho Y, Lee W B 2018 J. Phys. Chem. Lett. 9 1734
Google Scholar
[12] Banuti D T 2015 J. Supercrit. Fluids 98 12
Google Scholar
[13] Maxim F, Contescu C, Boillat P, Niceno B, Karalis K, Testino A, Ludwig C 2019 Nat. Commun. 10 1
Google Scholar
[14] Zhu B G, Xu J L, Wu X M, Xie J, Li M J 2019 J Int. J. Therm. Sci. 136 254
Google Scholar
[15] Xu J L, Zhang H S, Zhu B G, Xie J 2020 Sol. Energy 195 27
Google Scholar
[16] 张海松, 朱鑫杰, 朱兵国, 徐进良, 刘欢 2020 6 064401
Google Scholar
Zhang H S, Zhu X J, Zhu B G, Xu J L, Liu H 2020 Acta Phys. Sin. 6 064401
Google Scholar
[17] Yildiz S, Groeneveld D C 2014 Int. Commun. Heat Mass Transf. 54 27
Google Scholar
[18] 张思宇 2015 博士学位论文 (上海: 上海交通大学)
Zhang S Y 2015 Ph. D. Dissertation(Shanghai: Shanghai Jiaotong University) (in Chinese)
[19] Kang K H, Chang S H 2009 Int. J. Heat Mass Transfer 52 4946
Google Scholar
[20] Yamashita T, Yoshida S, Mori H, Morooka S, Komita H 2003 GENES4/ANP2003, Kyoto, Japan., Sep. 15–19, 2003 1119
[21] Lei X L, Li H X, Zhang W Q, Dinh N T, Guo Y M, Yu S Q 2017 Appl. Therm. Eng. 113 609
Google Scholar
[22] Shen Z, Yang D, Chen G M, Xiao F 2014 Int. J. Heat Mass Transfer 68 669
Google Scholar
[23] Buckingham E 1914 Phys. Rev. 4 345
[24] 罗峰, 胥蕊娜, 姜培学 2014 工程热 6 1170
Luo F, Xu R N, Jiang P X 2014 J. Eng. Thermophysics 6 1170
[25] 刘生晖, 黄彦平, 刘光旭, 王俊峰, 王金宇 2019 核动力工程 40 18
Google Scholar
Liu S H, Huang Y P, Liu G X, Wang J F, Wang J Y 2019 Nucl. Power Engineering 40 18
Google Scholar
[26] 廖长江, 李会雄 2015 工程热 1 111
Liao C J, Li H X 2015 J. Eng. Thermophysics 1 111
下载:
计量
- 文章访问数: 7219
- PDF下载量: 136
- 被引次数: 0
