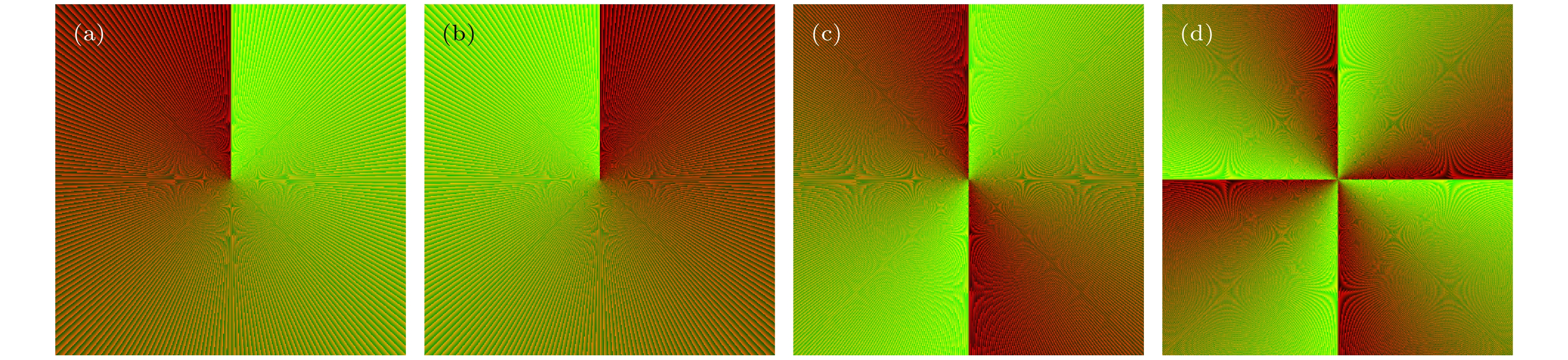
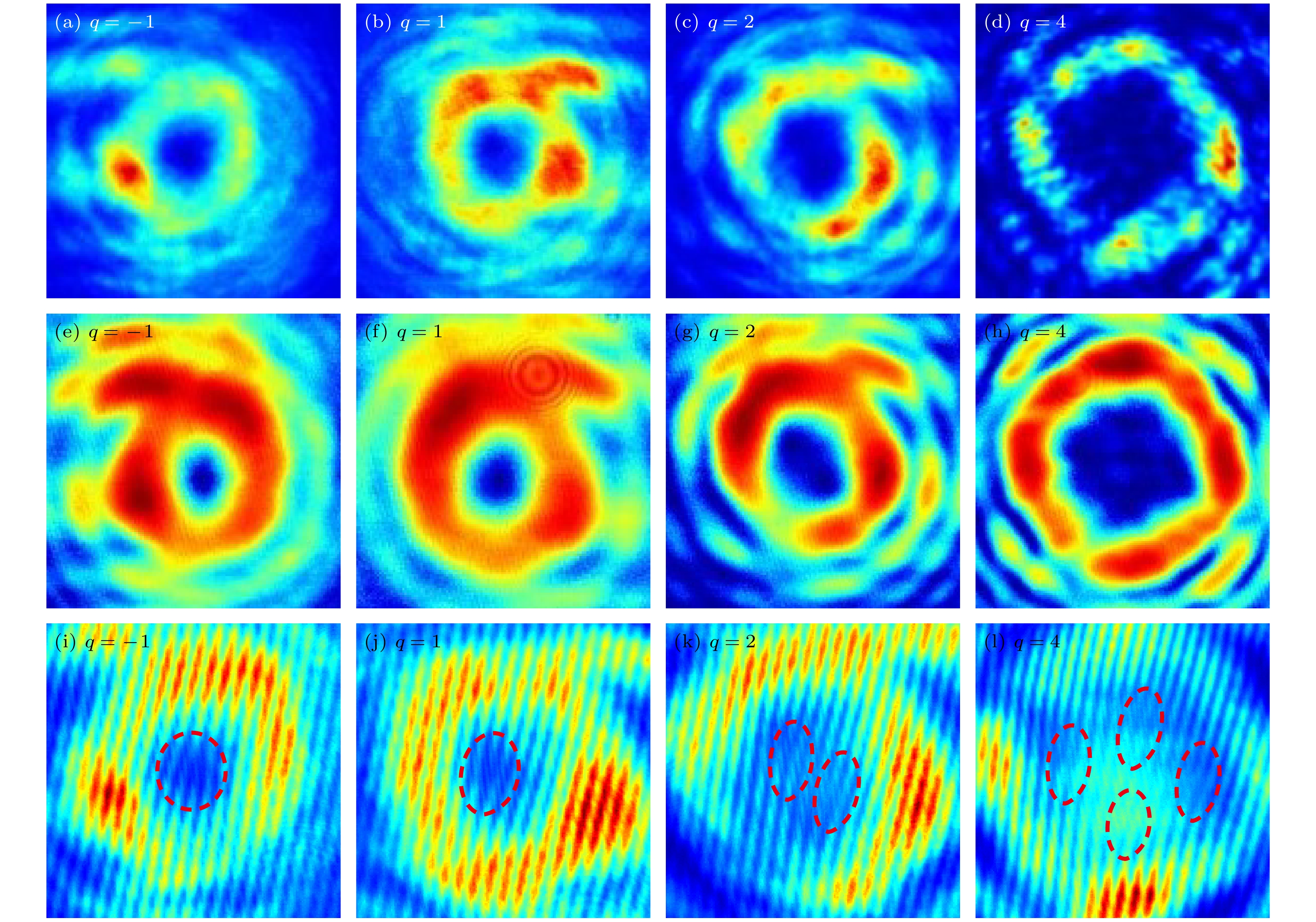
-
利用全息技术在偶氮聚合物薄膜中记录了拓扑荷数q = –1, 1, 2, 4的涡旋光场, 并将记录的原始叉形光栅与计算全息光栅进行对比, 对不同拓扑荷数涡旋光的记录速率和偶氮材料的可重复擦写性能进行了测试; 记录完成后, 将复现涡旋光与高斯光束干涉, 并与原始涡旋光和原始叉形光栅对比, 分析了记录质量. 实验结果表明：高阶涡旋光场的全息叉形光栅会在记录过程中发生劈裂, 轻微劈裂的涡旋光束仍维持一个稳定的环状结构; 全息记录过程中不同拓扑荷数的涡旋光束记录速率较为统一, 偶氮材料可经过上百次的擦写而不出现疲劳; 再现涡旋光与原始涡旋光在光强分布结构上保持高度一致, 再现涡旋光的干涉条纹与原始涡旋全息光栅保持高度一致, 涡旋光及其携带的拓扑荷信息可被有效记录和读取.In this paper the optical vortices with topological charge q = –1, 1, 2, 4 are recorded in azo polymer films by using holographic technology. The forked holographic gratings formed by the Gaussian beam and optical vortex beam are recorded in the sample films, the original forked holographic grating and the recording rate are analyzed. The vortex beam is reconstructed by illuminating the sample film with a reference beam, and the recording quality is analyzed. Also the erasability and durability of the sample are tested. The experimental results show that the recording rates of vortex beams with different topological charges are relatively uniform, which means that the optical vortices with different topological charges can be recorded at the same speed. The forked holographic grating of the high-order optical vortex splits in the recording process due to the disturbances, such as anisotropic nonlinear light, atmospheric turbulence, and background light field. However, the split vortex beam still maintains a stable ring structure. The reconstructed optical vortex and the original optical vortex are highly consistent in morphology, and the interference fringes of the reconstructed optical vortices are highly consistent with the original vortex holographic gratings, indicating that the topological charge information in the optical vortices can be effectively recorded and read out. The recorded information can be erased by heating the sample to about 97 ℃, and new information can be re-recorded after cooling. There appears no fatigue in the sample after the information has been erased 100 times and good durability is still retained. Optical vortices theoretically have infinite states of topological charges, based on which great success is achieved in optical communication and information encoding. Therefore, storing and reading information of topological charges in optical vortices may have potential applications in optical information storage.
-
Keywords:
- holography /
- azo polymer /
- optical vortex /
- topological charge
[1] Allen L, Beijersbergen M W, Spreeuw R J C, Woerdman J P 1992 Phys. Rev. A 45 8185
Google Scholar
[2] Mair A, Vaziri A, Weihs G, Zeilinger A 2001 Nature 412 313
Google Scholar
[3] Leach J, Padgett M J, Barnett S M, Franke-Arnold S, Courtial J 2002 Phys. Rev. Lett. 88 257901
Google Scholar
[4] Vaziri A, Weihs G, Zeilinger A 2002 Phys. Rev. Lett. 89 240401
Google Scholar
[5] Ding D S, Zhang W, Zhou Z Y, Shi S, Xiang G Y, Wang X S, Jiang Y K, Shi B S, Guo G C 2015 Phys. Rev. Lett. 114 050502
Google Scholar
[6] Schine N, Ryou A, Gromov A, Sommer A, Simon J 2016 Nature 534 671
Google Scholar
[7] Hamazaki J, Morita R, Chujo K, Kobayashi Y, Tanda S, Omatsu T 2010 Opt. Express 18 2144
Google Scholar
[8] Omatsu T, Chujo K, Miyamoto K, Okida M, Nakamura K, Aoki N, Morita R 2010 Opt. Express 18 17967
Google Scholar
[9] Toyoda K, Miyamoto K, Aoki N, Morita R, Omatsu T 2012 Nano Lett. 12 3645
Google Scholar
[10] Toyoda K, Takahashi F, Takizawa S, Tokizane Y, Miyamoto K, Morita R, Omatsu T 2013 Phys. Rev. Lett. 110 143603
Google Scholar
[11] Watanabe T, Igasaki Y, Fukuchi N, Sakai M, Ishiuchi S, Fujii M, Omatsu T, Yamamoto K, Iketaki Y 2004 Opt. Eng. 43 1136
Google Scholar
[12] Bretschneider S, Eggeling C, Hell S W 2007 Phys. Rev. Lett. 98 218103
Google Scholar
[13] Gahagan K T, Swartzlander G A 1996 Opt. Lett. 21 827
Google Scholar
[14] Padgett M, Bowman R 2011 Nat. Photonics 5 343
Google Scholar
[15] Padgett M J 2017 Opt. Express 25 11265
Google Scholar
[16] Barreiro J T, Wei T C, Kwiat P G 2008 Nat. Phys. 4 282
Google Scholar
[17] Nicolas A, Veissier L, Giner L, Giacobino E, Maxein D, Laurat J 2014 Nat. Photonics 8 234
Google Scholar
[18] Willner A E, Huang H, Yan Y, Ren Y, Ahmed N, Xie G, Bao C, Li L, Cao Y, Zhao Z, Wang J, Lavery M P J, Tur M, Ramachandran S, Molisch AF, Ashrafi N, Ashrafi S 2015 Adv. Opt. Photonics 7 66
Google Scholar
[19] Ren Y, Wang Z, Liao P, Li L, Xie G, Huang H, Zhao Z, Yan Y, Ahmed N, Willner A, Lavery M P, Ashrafi N, Ashrafi S, Bock R, Tur M, Djordjevic I B, Neifeld M A, Willner A E 2016 Opt. Lett. 41 622
Google Scholar
[20] Eznaveh Z S, Zacarias J C A, Lopez J E A, Shi K, Milione G, Jung Y, Thomsen B C, Richardson D J, Fontaine N, Leon-Saval S G, Correa R A 2018 Opt. Express 26 30042
Google Scholar
[21] Lugiato L A, Oldano C, Narducci L M 1988 Opt. Soc. Am. B 5 879
Google Scholar
[22] Brambilla M, Battipede F, Lugiato L A, Penna V, Prati F, Tamm C, Weiss C O 1991 Phys. Rev. A 43 5090
Google Scholar
[23] Oemrawsingh S S R, Ma X, Voigtand D, Aiello A, Eliel E R, Hooft G W, Woerdman J P 2005 Phys. Rev. Lett. 95 240501
Google Scholar
[24] Karimi E, Schulz S A, Leon I D, Qassim H, Upham J, Boyd R W 2014 Light Sci. Appl. 3 e167
Google Scholar
[25] Heckenberg N R, McDuff R, Smith C P, White A G 1992 Opt. Lett. 17 221
Google Scholar
[26] Leblanc A, Denoeud A, Chopineau L, Mennerat G, Martin P, Quéré F 2017 Nat. Phys. 13 440
Google Scholar
[27] Ambrosio A, Marrucci L, Borbone F, Roviello A, Maddalena P 2012 Nat. Commun. 3 989
Google Scholar
[28] Cook L J, Mazilu D A, Mazilu I, Simpson B M, Schwen E M, Kim V O, Seredinski A M 2014 Phys. Rev. E 89 062411
Google Scholar
[29] Mamaev A V, Saffman M, Zozulya A 1997 Phys. Rev. Lett. 78 2108
Google Scholar
[30] Gan X, Zhang P, Liu S, Zheng Y, Zhao J, Chen Z G 2009 Opt. Express 17 23130
Google Scholar
[31] Malik M, O’Sullivan M, Rodenburg B, Mirhosseini M, Leach J, Lavery M P, Padgett M J, Boyd R W 2012 Opt. Express 20 13195
Google Scholar
[32] Cui Q, Li M, Yu Z 2014 Opt. Commun. 329 10
Google Scholar
[33] Reddy S G, Prabhakar S, Aadhi A, Banerji J, Singh R P 2014 JOSA A 31 1295
Google Scholar
[34] Stoyanov L, Topuzoski S, Stefanov I, Janicijevic L, Dreischuh A 2015 Opt. Commun. 350 301
Google Scholar
-
图 1 偶氮苯聚合物薄膜的吸收光谱, 插图为样品AFM图像, 封装后的样品结构和化合物的化学结构
Fig. 1. Absorption spectra of the azo-benzene polymer film. Inset: AFM image and structure of the sample, and chemical structure of the compound.
图 2 涡旋全息记录实验装置. W1和W2, 记录光束; L1, 焦距为7.5 cm的凸透镜; L2, 焦距为20 cm的凸透镜; P, 偏振片; BS1, BS2, 分束器; A1, A2, A3, A4, 衰减片; M, M1, M2, M3, 反光镜; SLM, 空间光调制器
Fig. 2. Experimental setup for vortex holographic recording. W1 and W2, recording waves. L1, lens with a focal length of 7.5 cm; L2, lens with a focal length of 20 cm; P, polarizer; BS1, BS2, beam splitter; A1, A2, A3, A4, attenuator; M, M1, M2, M3, mirror; SLM, spatial light modulator.
图 3 用以产生不同拓扑荷数涡旋光束的相位图像配置文件 (a) q = –1; (b) q = 1; (c) q = 2; (d) q = 4
Fig. 3. Phase profiles displayed on the SLM to generate vortex beams with different topological charges q: (a) q = –1; (b) q = 1; (c) q = 2; (d) q = 4.
图 4 计算全息光栅与实验中记录的涡旋全息光栅的对比 (a)−(d)分别为q = –1, 1, 2, 4的计算全息光栅; (e)−(h)分别为实验中记录的q = –1, 1, 2, 4全息光栅
Fig. 4. Comparison between CGH gratings and vortex holographic gratings: (a)−(d) the CGH gratings of q = –1, 1, 2, 4; (e)−(h) vortex holographic gratings of q = –1, 1, 2, 4 recorded in experiments.
图 5 +1级衍射光斑强度的探测
Fig. 5. Detection of the intensity of the first order diffraction spot.
图 6 (a)衍射光斑强度随时间的变化; (b)涡旋全息光栅的衍射效率
Fig. 6. (a) Curves of the intensity variation of diffraction spots; (b) diffraction efficiency of optical vortex holographic grating.
图 7 高斯光束照射不同拓扑荷数涡旋光记录的全息光栅得到的衍射图样 (a) q = –1; (b) q = 1; (c) q = 2; (d) q = 4
Fig. 7. Diffraction images generated by using reference beam to illuminate samples with holograms recorded different topological charges: (a) q = –1; (b) q = 1; (c) q = 2; (d) q = 4.
图 8 (a)−(d)再现涡旋光束; (e)−(h)原始涡旋光束; (i)−(l)再现涡旋光束与高斯光束的干涉图样
Fig. 8. (a)−(d) Reconstructed optical vortex beams; (e)−(h) original optical vortex beam; (i)−(l) the interference pattern of reconstructed optical vortex beam and Gaussian beam.
-
[1] Allen L, Beijersbergen M W, Spreeuw R J C, Woerdman J P 1992 Phys. Rev. A 45 8185
Google Scholar
[2] Mair A, Vaziri A, Weihs G, Zeilinger A 2001 Nature 412 313
Google Scholar
[3] Leach J, Padgett M J, Barnett S M, Franke-Arnold S, Courtial J 2002 Phys. Rev. Lett. 88 257901
Google Scholar
[4] Vaziri A, Weihs G, Zeilinger A 2002 Phys. Rev. Lett. 89 240401
Google Scholar
[5] Ding D S, Zhang W, Zhou Z Y, Shi S, Xiang G Y, Wang X S, Jiang Y K, Shi B S, Guo G C 2015 Phys. Rev. Lett. 114 050502
Google Scholar
[6] Schine N, Ryou A, Gromov A, Sommer A, Simon J 2016 Nature 534 671
Google Scholar
[7] Hamazaki J, Morita R, Chujo K, Kobayashi Y, Tanda S, Omatsu T 2010 Opt. Express 18 2144
Google Scholar
[8] Omatsu T, Chujo K, Miyamoto K, Okida M, Nakamura K, Aoki N, Morita R 2010 Opt. Express 18 17967
Google Scholar
[9] Toyoda K, Miyamoto K, Aoki N, Morita R, Omatsu T 2012 Nano Lett. 12 3645
Google Scholar
[10] Toyoda K, Takahashi F, Takizawa S, Tokizane Y, Miyamoto K, Morita R, Omatsu T 2013 Phys. Rev. Lett. 110 143603
Google Scholar
[11] Watanabe T, Igasaki Y, Fukuchi N, Sakai M, Ishiuchi S, Fujii M, Omatsu T, Yamamoto K, Iketaki Y 2004 Opt. Eng. 43 1136
Google Scholar
[12] Bretschneider S, Eggeling C, Hell S W 2007 Phys. Rev. Lett. 98 218103
Google Scholar
[13] Gahagan K T, Swartzlander G A 1996 Opt. Lett. 21 827
Google Scholar
[14] Padgett M, Bowman R 2011 Nat. Photonics 5 343
Google Scholar
[15] Padgett M J 2017 Opt. Express 25 11265
Google Scholar
[16] Barreiro J T, Wei T C, Kwiat P G 2008 Nat. Phys. 4 282
Google Scholar
[17] Nicolas A, Veissier L, Giner L, Giacobino E, Maxein D, Laurat J 2014 Nat. Photonics 8 234
Google Scholar
[18] Willner A E, Huang H, Yan Y, Ren Y, Ahmed N, Xie G, Bao C, Li L, Cao Y, Zhao Z, Wang J, Lavery M P J, Tur M, Ramachandran S, Molisch AF, Ashrafi N, Ashrafi S 2015 Adv. Opt. Photonics 7 66
Google Scholar
[19] Ren Y, Wang Z, Liao P, Li L, Xie G, Huang H, Zhao Z, Yan Y, Ahmed N, Willner A, Lavery M P, Ashrafi N, Ashrafi S, Bock R, Tur M, Djordjevic I B, Neifeld M A, Willner A E 2016 Opt. Lett. 41 622
Google Scholar
[20] Eznaveh Z S, Zacarias J C A, Lopez J E A, Shi K, Milione G, Jung Y, Thomsen B C, Richardson D J, Fontaine N, Leon-Saval S G, Correa R A 2018 Opt. Express 26 30042
Google Scholar
[21] Lugiato L A, Oldano C, Narducci L M 1988 Opt. Soc. Am. B 5 879
Google Scholar
[22] Brambilla M, Battipede F, Lugiato L A, Penna V, Prati F, Tamm C, Weiss C O 1991 Phys. Rev. A 43 5090
Google Scholar
[23] Oemrawsingh S S R, Ma X, Voigtand D, Aiello A, Eliel E R, Hooft G W, Woerdman J P 2005 Phys. Rev. Lett. 95 240501
Google Scholar
[24] Karimi E, Schulz S A, Leon I D, Qassim H, Upham J, Boyd R W 2014 Light Sci. Appl. 3 e167
Google Scholar
[25] Heckenberg N R, McDuff R, Smith C P, White A G 1992 Opt. Lett. 17 221
Google Scholar
[26] Leblanc A, Denoeud A, Chopineau L, Mennerat G, Martin P, Quéré F 2017 Nat. Phys. 13 440
Google Scholar
[27] Ambrosio A, Marrucci L, Borbone F, Roviello A, Maddalena P 2012 Nat. Commun. 3 989
Google Scholar
[28] Cook L J, Mazilu D A, Mazilu I, Simpson B M, Schwen E M, Kim V O, Seredinski A M 2014 Phys. Rev. E 89 062411
Google Scholar
[29] Mamaev A V, Saffman M, Zozulya A 1997 Phys. Rev. Lett. 78 2108
Google Scholar
[30] Gan X, Zhang P, Liu S, Zheng Y, Zhao J, Chen Z G 2009 Opt. Express 17 23130
Google Scholar
[31] Malik M, O’Sullivan M, Rodenburg B, Mirhosseini M, Leach J, Lavery M P, Padgett M J, Boyd R W 2012 Opt. Express 20 13195
Google Scholar
[32] Cui Q, Li M, Yu Z 2014 Opt. Commun. 329 10
Google Scholar
[33] Reddy S G, Prabhakar S, Aadhi A, Banerji J, Singh R P 2014 JOSA A 31 1295
Google Scholar
[34] Stoyanov L, Topuzoski S, Stefanov I, Janicijevic L, Dreischuh A 2015 Opt. Commun. 350 301
Google Scholar
下载:
计量
- 文章访问数: 5378
- PDF下载量: 81
- 被引次数: 0
