-
无磁光学非互易在量子通信、量子网络和光信息处理等方面具有重要的应用. 本文通过简并二能级热原子系统, 在单向泵浦场作用下, 考虑热原子的多普勒效应, 实现双路简并四波混频信号的非互易放大. 在此基础上, 再引入一束对向共线传播的泵浦场, 形成了空间复用的多重四波混频过程, 从而实现了双通道四波混频信号的互易放大. 进一步, 利用多组涡旋相位片分别对信号光和泵浦光加载螺旋相位, 产生携带光学轨道角动量的高阶拉盖尔-高斯涡旋光束, 并参与到四波混频过程中, 实现了泵浦光的轨道角动量向增益光场的转移; 同时利用马赫-曾德尔干涉仪, 进一步分析了各路四波混频信号场在非互易-互易放大转换下, 光学轨道角动量的守恒特性. 该结论为实现基于复杂结构光的光学非互易器件的应用研究提供了重要的参考.Magnet-free optical nonreciprocity has significant applications in quantum communication, quantum networks, and optical information processing. In this research, considering a degenerate two-level thermal atomic system with the Doppler effect of thermal atoms, the nonreciprocal amplification (NRA) of dual-path degenerate four-wave mixing (FWM) signals is achieved under the action of a co-propagating pumping field. On this basis, spatially multiplexed multiple FWM processes are formed by introducing another counter-propagating pumping field, thereby achieving the reciprocal amplification (RA) of the dual-channel FWM signals. Furthermore, by using multiple sets of spiral phase plates to load spiral phases on the signal light and the pumping light respectively, higher-order Laguerre-Gaussian vortex beams carrying different optical orbital angular momentum (OAM) are generated and participate in the FWM process, achieving the transfer of the OAM of the pumping light to the amplified FWM fields. Simultaneously, using the Mach-Zehnder interferometer, the conservation characteristics of the OAM of each FWM signal in the NRA-RA conversion are further analyzed. Furthermore, experimental results demonstrate that in the multiple FWM process induced by a pair of counter-propagating pump fields, the OAM of the amplified FWM signal in each channel varies with that of the pump field. However, the overall process maintains the OAM conservation. This study provides a feasible solution for expanding the channel capacity using OAM based on NRA-RA system, showing that the OAM has potential application prospects in achieving high-capacity optical communication and multi-channel signal processing.
-
Keywords:
- optical nonreciprocity /
- four-wave mixing /
- optical orbital angular momentum /
- vortex beam
-
图 1 (a)实验能级示意图; (b)实验装置示意图; (c)泵浦光与信号光在Cs原子气室中相互作用角度示意图
Fig. 1. (a) Diagram of atom energy levels for the atoms; (b) diagram of experimental setup; (c) diagram of the interaction angle between pump and signal lights in the Cs atom cell.
图 2 不同泵浦光和信号光条件下, 四路探测器(PD1—PD4)测量的归一化透射谱T随单光子失谐Δ的变化趋势 (a) P1-S1; (b) P2-S1; (c) P1-P2-S1; (d) P1-S2; (e) P2-S2; (f) P1-P2-S2. 主要实验参量: $ {P_{{{\mathrm{P}}_1}}} = {P_{{{\mathrm{P}}_2}}} = 10\;{\text{mW}} $, $ {P_{{{\mathrm{S}}_1}}} = {P_{{{\mathrm{S}}_2}}} = 5\;{\text{μW}} $, $ {T_{\text{c}}} = 100 $ ℃
Fig. 2. Normalized transmission spectra T detected by PD1–PD4 versus single detuning Δ under the different pump and signal lights: (a) P1-S1; (b) P2-S1; (c) P1-P2-S1; (d) P1-S2; (e) P2- S2; (f) P1-P2-S2. The main experimental parameters are: $ {P_{{{\mathrm{P}}_1}}} = {P_{{{\mathrm{P}}_2}}} = 10\;{\text{mW}} $, $ {P_{{{\mathrm{S}}_1}}} = {P_{{{\mathrm{S}}_2}}} = 5\;{\text{μW}} $, $ {T_{\text{c}}} = 100 $ ℃.
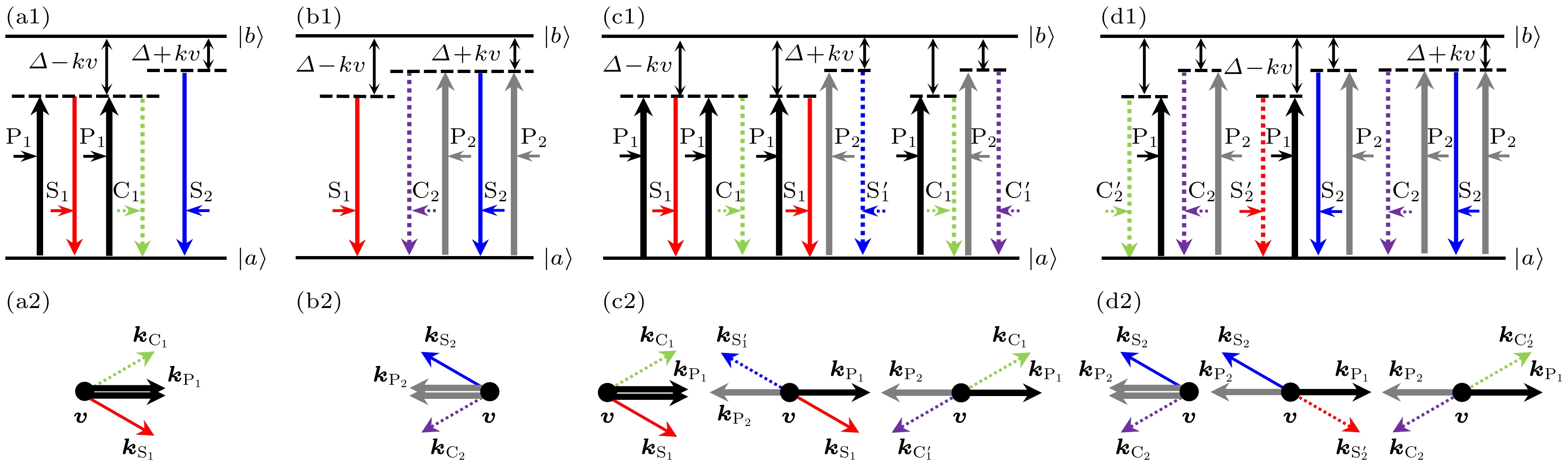
图 3 不同泵浦光和信号光条件下的FWM过程 (a1) P1-S1; (b1) P2-S2; (c1) P1-P2-S1; (d1) P1-P2-S2. (a2)—(d2) 对应图(a1)—(d1)条件下FWM过程的相位匹配关系
Fig. 3. The FWM processes under the different pump and signal lights: (a1) P1-S1; (b1) P2-S2; (c1) P1-P2-S1; (d1) P1-P2-S2. (a2)–(d2) Phase matching corresponding to the FWM of panels (a1)–(d1).
图 4 (a1)—(d1)和(a2)—(d2)分别对应图3(a1)—(d1)的FWM过程中, 从前向和后向探测方向观测的光斑图样. 单光子失谐为Δ ≈ –260 MHz
Fig. 4. (a1)–(d1) and (a2)–(d2) Spatial patterns of FWM beams generated in the forward and backward directions corresponding to the FWM processes in Figs. 3 (a1)–(d1). The single photon detuning is Δ ≈ –260 MHz.
图 5 (a1)—(c1)在NRA条件下, 信号光和泵浦光携带不同OAM时CCD观测的光斑图样 (a1) ${l_{{{\text{S}}_1}}} = - 1$, ${l_{{{\text{P}}_1}}} = 0$; (b1) ${l_{{{\text{S}}_1}}} = 0$, ${l_{{{\text{P}}_1}}} = - 1$; (c1) ${l_{{{\text{S}}_2}}} = 0$, ${l_{{{\text{P}}_2}}} = 2$. (a2)—(c3)分别对应图(a1)—(c1)中相应放大FWM信号的干涉图样
Fig. 5. (a1)–(c1) Under NRA condition, the Spatial patterns observed by the CCD when the signal and pump lights carry different OAM: (a1) ${l_{{{\text{S}}_1}}} = - 1$, ${l_{{{\text{P}}_{1}}}} = 0$; (b1) ${l_{{{\text{S}}_1}}} = 0$, ${l_{{{\text{P}}_1}}} = - 1$; (c1) ${l_{{{\text{P}}_2}}} = 2$, ${l_{{{\text{P}}_{2}}}} = 2$. (a2)–(c3) Interference patterns of the amplified FWM signals corresponding to panels (a1)–(c1).
图 6 RA条件下, 信号光和泵浦光携带不同OAM时(a1), (c1)前向CCD和(b1), (d1)后向CCD观测的光斑图样 (a1), (b1) ${l_{{{\mathrm{S}}_1}}} = - 1$, ${l_{{{\mathrm{P}}_1}}} = {l_{{{\mathrm{P}}_2}}} = 0$; (c1), (d1) ${l_{{{\mathrm{S}}_1}}} = 0$, ${l_{{{\text{P}}_1}}} = - 1$, ${l_{{{\text{P}}_2}}} = 2$. (a2)—(d3)分别对应图(a1)—(d1)中相应放大FWM信号的干涉图样
Fig. 6. Under the condition of RA, the spatial patterns observed by the forward CCD (a1) and (c1), as well as the backward CCD (b1) and (d1) when the signal and pump lights carry different OAM: (a1), (b1) ${l_{{{\text{S}}_1}}} = - 1$, ${l_{{{\text{P}}_1}}} = {l_{{{\text{P}}_2}}} = 0$; (c1), (d1) ${l_{{{\text{S}}_1}}} = 0$, ${l_{{{\text{P}}_1}}} = - 1$, ${l_{{{\text{P}}_2}}} = 2$. (a2)–(d3) Interference patterns of the amplified FWM signals corresponding to panels (a1)–(d1).
表 1 四路放大FWM信号光的OAM值
Table 1. Value of OAM for 4 ways FWM signals.
${l_{{{\text{S}}_1}}}$ ${l_{{{\text{C}}_{1}}}}$ ${l_{{{{\text{S'}}}_{1}}}}$ ${l_{{{{\text{C'}}}_{1}}}}$ ${l_{{{\text{S}}_{2}}}}$ ${l_{{{\text{C}}_2}}}$ ${l_{{{{\text{S}}}'_{2}}}}$ $ {l_{{{{\text{C}}}'_{2}}}} $ ${l_{{{\text{P}}_1}}} = - 1$, ${l_{{{\text{P}}_{2}}}} = 0$ 0 –2 1 –1 0 0 –1 –1 ${l_{{{\text{P}}_1}}} = - 1$, ${l_{{{\text{P}}_{2}}}} = - 1$ 0 –2 0 –2 0 –2 0 –2 ${l_{{{\text{P}}_1}}} = - 1$, ${l_{{{\text{P}}_{2}}}}{=}1$ 0 –2 2 0 0 2 –2 0 ${l_{{{\text{P}}_{1}}}} = - 1$, ${l_{{{\text{P}}_{2}}}} = - 2$ 0 –2 –1 –3 0 –4 1 –3 ${l_{{{\text{P}}_{1}}}} = - 1$, ${l_{{{\text{P}}_{2}}}} = 2$ 0 –2 3 1 0 4 –3 1 
下载: 导出CSV
-
[1] Dimitrios L. Sounas, Andrea Alù 2017 Nat. Photonics 11 774
Google Scholar
[2] Yang H, Zhang S, Niu Y, Gong S 2022 Opt. Commun. 515 128195
Google Scholar
[3] Cirac J I, Zoller P, Kimble H J, Mabuchi H 1997 Phys. Rev. Lett. 78 3221
Google Scholar
[4] Yu Z F, Fan S H 2009 Nat. Photonics 3 91
Google Scholar
[5] Aplet L J, Carson J W 1964 Appl. Opt. 3 544
Google Scholar
[6] Bi L, Hu J, Jiang P, Kim D H, Dionne G F, Kimerling L C, Ross C A 2011 Nat. Photonics 5 758
Google Scholar
[7] 汪静丽, 皇甫利国, 陈鹤鸣 2021 光学学报 41 0713001
Google Scholar
Wang J L, Huangfu L G, Chen H M 2021 Acta Opt. Sin. 41 0713001
Google Scholar
[8] Poo Y, Wu R xin, Lin Z, Yang Y, Chan C T 2011 Phys. Rev. Lett. 106 093903
Google Scholar
[9] Zhu L, Fan S 2016 Phys. Rev. Lett. 117 134303
Google Scholar
[10] Muñoz de las Heras A, Carusotto I 2022 Phys. Rev. A 106 063523
Google Scholar
[11] Tian H, Liu J Q, Siddharth A, Wang R N, Blésin T, He J J, Kippenberg T J, Bhave S A 2021 Nat. Photonics 15 828
Google Scholar
[12] Yu Y, Chen Y H, Hu H, Xue W Q, Yvind K, Mork J 2014 Laser Photonics Rev. 9 241
[13] Fan L, Wang J, Varghese L T, Shen H, Niu B, Xuan Y, Weiner A M, Qi M 2012 Science 335 447
Google Scholar
[14] Sounas D L, Caloz C, Alù A 2013 Nat. Commun. 4 2407
Google Scholar
[15] Zhou H, Zhou K F, Hu W, Guo Q, Lan S, Lin X S, Gopal A V 2006 Appl. Phys. Lett. 99 123111
[16] Li E Z, Ding D S, Yu Y C, Dong M X, Zeng L, Zhang W H 2020 Phys. Rev. Res. 2 033517
Google Scholar
[17] Sayrin C, Junge C, Mitsch R, Albrecht B, O’Shea D, Schneeweiss P, Volz J, Rauschenbeutel A 2015 Phys. Rev. X 5 041036
[18] Scheucher M, Hilico A, Will E, Volz J, Rauschenbeutel A 2016 Science 354 1577
Google Scholar
[19] Tang L, Tang J, Zhang W, Lu G, Zhang H, Zhang Y, Xia K, Xiao M 2019 Phys. Rev. A 99 043833
Google Scholar
[20] Sounas D L, Alù A 2017 Nat. Photonics 11 774
Google Scholar
[21] Wang J, Herrmann J F, Witmer J D, Safavi-Naeini A H, Fan S 2021 Phys. Rev. Lett. 126 193901
Google Scholar
[22] Yu Z, Fan S 2009 Appl. Phys. Lett. 94 171116
Google Scholar
[23] Hafezi M, Rabl P 2012 Opt. Express 20 7672
Google Scholar
[24] Xu H, Jiang L Y, Clerk A A, Harris G E 2019 Nature 568 65
Google Scholar
[25] Aspelmeyer M, Kippenberg T J, Marquardt F 2014 Rev. Mod. Phys. 86 1391
Google Scholar
[26] Wang D W, Zhou H T, Guo M J, Zhang J X, Evers J, Zhu S Y 2013 Phys. Rev. Lett. 110 093901
Google Scholar
[27] Dong M X, Xia K Y, Zhang W H, Yu C Y, Ye Y H, Li E Z, Zeng L, Ding D S, Shi B S, Guo G C, Nori F 2021 Sci. Adv. 7 8924
Google Scholar
[28] Zhang S, Hu Y, Lin G, Niu Y, Xia K, Gong J, Gong S 2018 Nat. Photonics 12 744
Google Scholar
[29] 李鑫, 解舒云, 李林帆, 周海涛, 王丹, 杨保东 2022 71 184202
Google Scholar
Li X, Xie S Y, Li L F, Zhou H T, Wang D, Yang B D 2022 Acta Phys. Sin. 71 184202
Google Scholar
[30] 李观荣, 郑怡婷, 徐琼怡, 裴笑山, 耿玥, 严冬, 杨红 2024 73 126401
Google Scholar
Li R G, Zheng Y T, Xu Q Y, Pei X S, Geng Y, Yan D, Yang H 2024 Acta Phys. Sin. 73 126401
Google Scholar
[31] Lin G, Zhang S, Hu Y, Niu Y, Gong J, Gong S 2019 Phys. Rev. Lett. 123 033902
Google Scholar
[32] Lü S, Jing J 2017 Phys. Rev. A 96 043873
Google Scholar
[33] Liu S, Lou Y, Jing J 2019 Phys. Rev. Lett. 123 113602
Google Scholar
[34] 余胜, 刘焕章, 刘胜帅, 荆杰泰 2020 69 090303
Google Scholar
Yu S, Liu H Z, Liu S S, Jing J T 2020 Acta Phys. Sin. 69 090303
Google Scholar
[35] Liang C, Liu B, Xu A N, Wen X, Lu C, Xia K, Tey M K, Liu Y C, You L 2020 Phys. Rev. Lett. 125 123901
Google Scholar
[36] Lassen M, Delaubert V, Harb C C, Treps N, Lam P K, Bachor H A 2006 J. Eur. Opt. Soc. - Rapid Publ. 1 06003
Google Scholar
[37] Lassen M, Leuchs G, Andersen U L 2009 Phys. Rev. Lett. 102 163602
Google Scholar
[38] Wang X, Jing J 2022 Phys. Rev. A 18 024057
Google Scholar
[39] Nicolas A, Veissier L, Giner L, Giacobino E, Maxein D, Laurat J 2014 Nat. Photonics 8 234
Google Scholar
[40] Ding D S, Zhou Z Y, Shi B S, Guo G C 2013 Nat. Commun. 4 2527
Google Scholar
[41] Arita Y, Chen M, Wright E M, Dholakia K 2017 J. Opt. Soc. Am. B: Opt. Phys. 34 C14
Google Scholar
[42] Liang Y, Lei M, Yan S, Li M, Cai Y, Wang Z, Yu X, Yao B 2018 Appl. Opt. 57 79
Google Scholar
[43] Pan X, Yu S, Zhou Y, Zhang K, Zhang K, Lü S, Li S, Wang W, Jing J 2019 Phys. Rev. Lett. 123 070506
Google Scholar
[44] Li S, Pan X, Ren Y, Liu H, Yu S, Jing J 2020 Phys. Rev. Lett. 124 083605
Google Scholar
[45] Zhou H T, Guo M J, Wang D, Gao J R, Zhang J X, Zhu S Y 2011 J. Phys. B: At. Mol. Opt. Phys. 44 225503
Google Scholar
[46] Grischokowsky D 1970 Phys. Rev. Lett. 24 1663
下载:
计量
- 文章访问数: 475
- PDF下载量: 12
- 被引次数: 0
