-
拓扑现象对于病毒颗粒的空间分布、高分子聚合物纳米囊泡的成型以及玻色-爱因斯坦凝聚物等方面都发挥着重要作用. 本文利用Landau-de Gennes理论, 构建模型来模拟液晶中拓扑荷分布及其他现象. 通过对数值模型序参量场的演化, 以及模拟液晶薄膜中所生成的拓扑荷之间的相互作用来分析液晶(Lqc)薄膜的尺寸对拓扑荷的影响. 研究结果表明,随着液晶盘半径增大, 拓扑荷间最优距离与半径之比渐增并趋于稳定. 此研究结论对利用拓扑荷凝聚颗粒物效应设计分离容器有指导意义, 有助于进一步理解拓扑胶体和液晶以及液晶共聚物等软物质中的拓扑现象.
-
关键词:
- 向列相液晶 /
- 相场 /
- 拓扑荷 /
- Landau-de Gennes模型
Algebraic topology, algebraic geometry, and category theory are new branches of mathematics that have developed in the last hundred years and have had profound collisions with modern physics in recent decades. A large number of topological phenomena are found in systems such as viruses, bacteria, fingerprints, fish school, typhoons, and the galaxies. Topological phenomena play a significant role in the spatial distribution of viral particles, the formation of nanovesicles of polymer, and Bose-Einstein condensates. In this paper, based on Landau-de Gennes theory, models have been constructed to simulate the topological charge distribution and other topological phenomena in liquid crystals. The research indicates that as the radius of the liquid crystal panel grows, the ratio of the optimal distance between the topological charge to the radius gradually increases and tends to stabilize. The size of the disc affects the equilibrium position of the topological load. The relative equilibrium position of topological load is between 0.542 and 0.558, in which the ratio of the distance between the two +1/2 topological loads in the 0–5 mm disc increases from 0.542 to 0.558, and then in the 5–12 mm section the ratio is almost stable at 0.558. As the size of the disc increases, the influence of the boundary anchoring energy decreases, and the equilibrium position, i.e. the distance between the two topological charges and the diameter of the disc, approaches a constant value. This equilibrium position is the result of the repulsive force of the disc boundary on the +1/2 topological load and the repulsive force between the two topological loads. The angle between two topological charges in a liquid crystal disc is between 140° and 180°. The trajectory of the topological charge is the process of finding the lowest free energy point, and the end of the trajectory is in the region of minimum free energy. The result is instructive significance in the design of classification containers by using topological charge condensate effect. And it is helpful to further understand the topological phenomena in soft materials including topological colloids, liquid crystals, and liquid crystal copolymers.-
Keywords:
- nematic liquid crystal /
- phase-field /
- topological charge /
- Landau-de Gennes model
[1] Crawford G P, Zumer S 1996 Liquid Crystals in Complex Geometries: Formed by Polymer and Porous Networks (CRC Press: Boca Raton) p521
[2] Takeuchi H, Tsubota M 2006 J. Phys. Soc. Jpn. 75 063601
Google Scholar
[3] Joyce D D 2000 Compact Manifolds with Special Holonomy (Oxford: Oxford University Press) p395.
[4] Dammone O J, Zacharoudiou I, Dullens R P, Yeomans J M, Lettinga M P, Aarts D G 2012 Phys. Rev. Lett. 109 108303
Google Scholar
[5] Duclos G, Adkins R, Banerjee D, Peterson M S E, Varghese M, Kolvin I, Baskaran A, Pelcovits R A, Powers T R, Baskaran A, Toschi F, Hagan M F, Streichan S J, Vitelli V, Beller D A, Dogic Z 2020 Science 367 1120
Google Scholar
[6] Manyuhina O V, Lawlor K B, Marchetti M C, Bowick M J 2015 Soft Matter 11 6099
Google Scholar
[7] Smalyukh I I, Lansac Y, Clark N A, Trivedi R P 2010 Nat. Mater. 9 139
Google Scholar
[8] Senyuk B, Liu Q, He S, Kamien R D, Kusner R B, Lubensky T C, Smalyukh Ⅱ 2013 Nature 493 200
Google Scholar
[9] 刘永军, 孙伟民, 刘晓颀, 姚丽双, 鲁兴海, 宣丽 2012 61 114211
Google Scholar
Liu Y J, Sun W M, Liu X Q, Yao L S, Lu X H, Xuan L 2012 Acta Phys. Sin. 61 114211
Google Scholar
[10] 吕月兰, 尹向宝, 杨月, 刘永军, 苑立波 2017 66 154205
Google Scholar
Lü Y L, Yin X B, Yang Y, Liu Y J, Yuan L B 2017 Acta Phys. Sin. 66 154205
Google Scholar
[11] Ackerman P J, van de Lagemaat J, Smalyukh Ⅱ 2015 Nat. Commun. 6 6012
Google Scholar
[12] Xing X, Shin H, Bowick M J, Yao Z, Jia L, Li M H 2012 Proc. Natl. Acad. Sci. U. S. A 109 5202
Google Scholar
[13] Opathalage A, Norton M M, Juniper M P N, Langeslay B, Aghvami S A, Fraden S, Dogic Z 2019 Proc. Natl. Acad. Sci. U. S. A. 116 4788
Google Scholar
[14] Dolganov P V, Cluzeau P, Dolganov V K 2019 Liq. Cryst. Rev. 7 1
Google Scholar
[15] Peng C, Lavrentovich O D 2019 Micromachines-Basel 10 02187
[16] Turiv T, Krieger J, Babakhanova G, Yu H, Shiyanovskii S V, Wei Q H, Kim M H, Lavrentovich O D 2020 Sci. Adv. 6 eaaz6485
Google Scholar
[17] Giomi L, Kos Z, Ravnik M, Sengupta A 2017 Proc. Natl. Acad. Sci. U. S. A. 11 4
[18] Liu Q, Senyuk B, Tasinkevych M, Smalyukh Ⅱ 2013 Proc. Natl. Acad. Sci. U. S. A. 110 9231
Google Scholar
[19] Solodkov N V, Shim J U, Jones J C 2019 Nat. Commun. 10 198
Google Scholar
[20] Liang D, Ma X, Liu Z, Jafri H M, Cao G, Huang H, Shi S, Chen L Q 2020 J. Appl. Phys. 128 124701
Google Scholar
[21] Tang X, Selinger J V 2017 Soft Matter 13 5481
Google Scholar
[22] De Gennes P G, Prost J 1993 The Physics of Liquid Crystals (Vol. 83) (New York: Oxford University Press) p597.
[23] Pelka R, Saito K 2006 Phys. Rev. E 74 041705
Google Scholar
[24] Frank F C 1958 Discuss. Faraday Soc. 25 19
Google Scholar
[25] Berreman D W, Meiboom S 1984 Phys. Rev. A 30 1955
Google Scholar
[26] Longa L, Monselesan D, Trebin H R 1987 Liq. Cryst. 2 769
Google Scholar
[27] Inukai T, Miyazawa K 1917 Outline of Development of Nematic Liquid Crystal Compounds for LCD (The Museum: King's Printer for British Columbia) p559.
[28] Fournier J B, Galatola P 2005 Europhys. Lett. 72 403
Google Scholar
[29] Duclos G, Erlenkämper C, Joanny J F, Silberzan P 2017 Nat. Phys. 13 58
Google Scholar
-
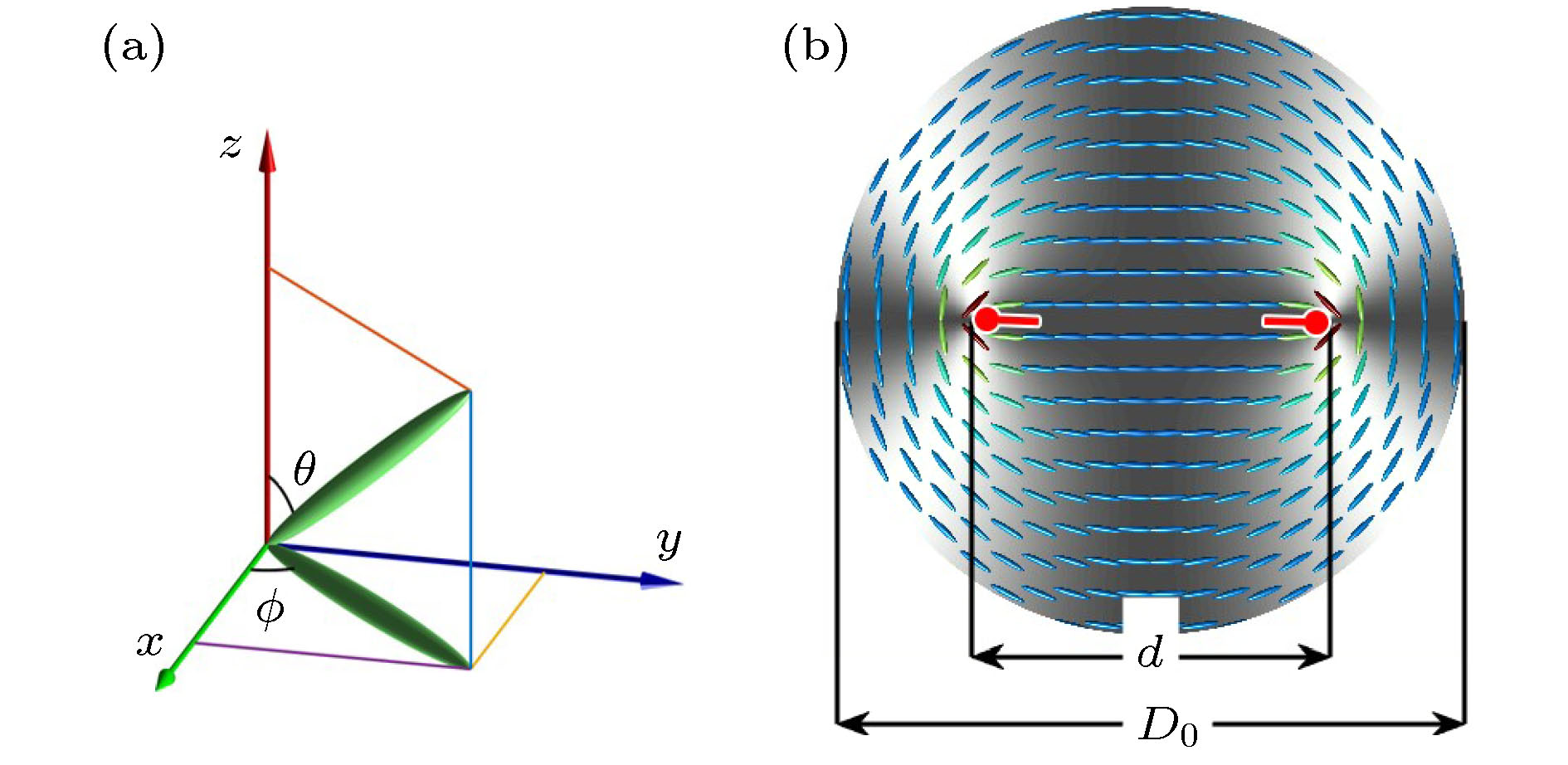
图 1 (a) 液晶指向矢与空间坐标轴之间夹角的示意图; (b) 液晶圆盘直径D0和两个大小为
$ + {1}/{2} $ 拓扑荷之间距离d的示意图, 红色标记表示$ + {1}/{2} $ 拓扑荷Fig. 1. (a) Schematic of the angle between director of liquid crystal and the spatial axis; (b) schematic of the NLqc disc diameter D0 and d the distance between two topological charges,
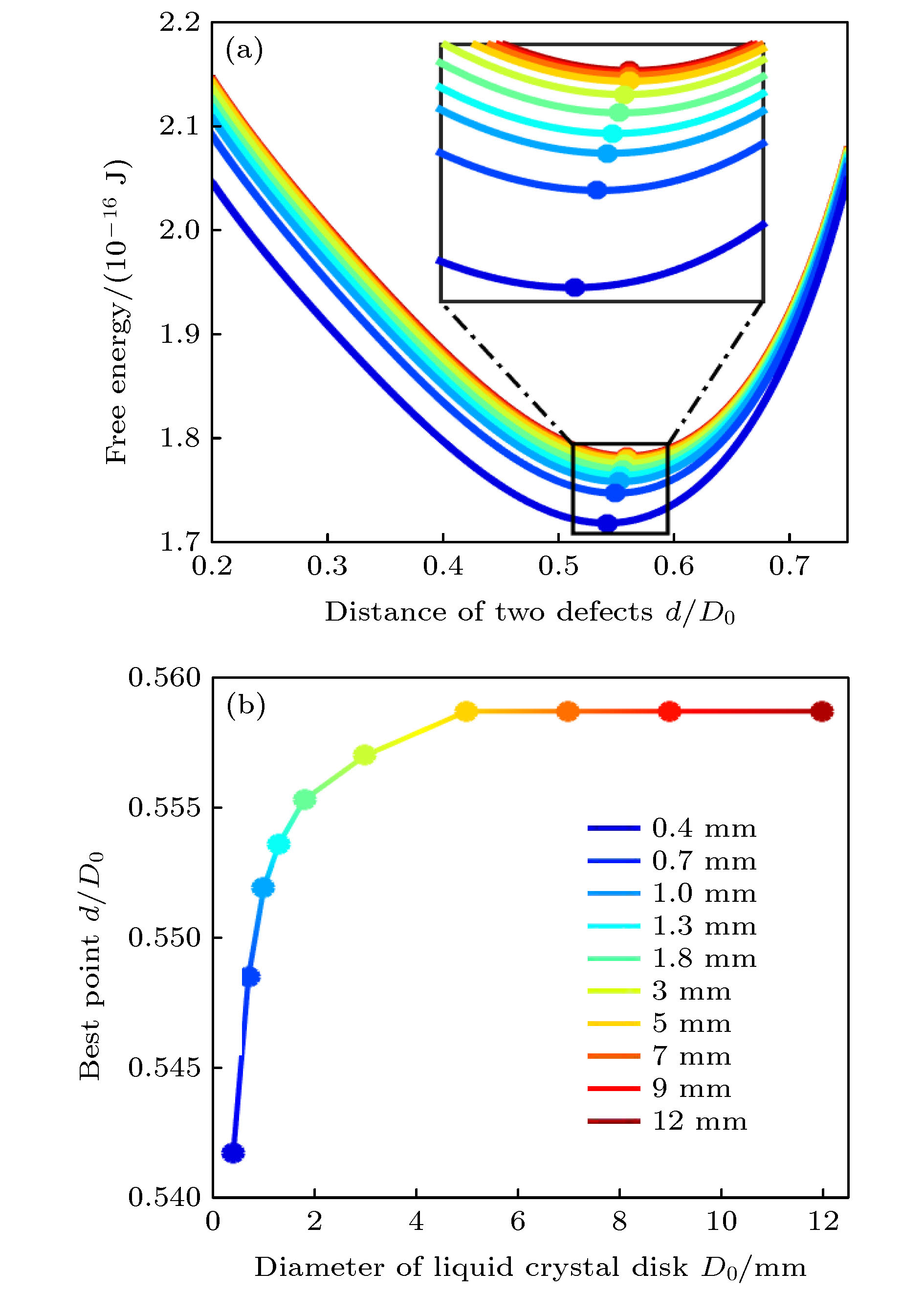
$ + {1}/{2} $ topological charges represented by red markers.
图 2 (a) 直径分别为0.4−12 mm圆盘中液晶薄膜自由能随中心两个拓扑荷的间距变化曲线; (b) 两个拓扑荷的最优位置随液晶圆盘直径变化的趋势图
Fig. 2. (a) The free energy of liquid crystal film in a disk with diameters ranging from 0.4 mm to 12 mm as a function of the distance between the two topological charges; (b) the trend of the optimal position of the two topological charges as a function of the diameter of the liquid crystal disk.
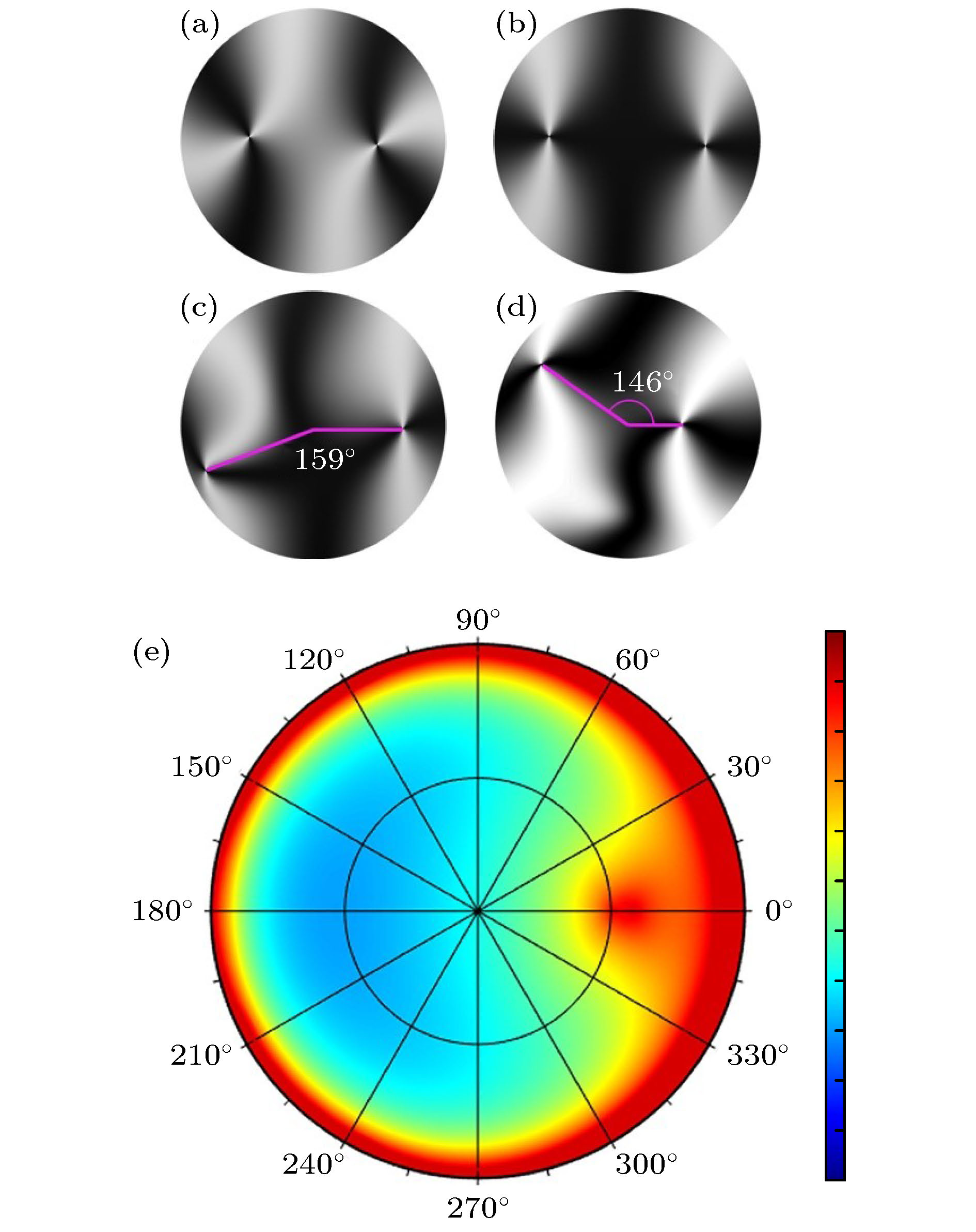
图 3 (a)−(d)偏光镜图片 (a), (b) 圆盘直径为0.4和 12 mm时得到的平衡位置POM图; (c), (d)计算模拟的接近最终平衡位置的偏光显微镜图片. (e) 自由能随角度和位置变化的分布图
Fig. 3. (a)−(d) are polarizing optical microscope images: (a), (b) are POM images of the optimal positions for disk diameters of 0.4 and 12 mm, respectively; (c), (d) POM images of a near-final optimal position obtained from computational simulation. (e) Free energy as a function of position.
图 4 十个不同相对位置的拓扑荷演化过程的运动迹图
Fig. 4. Motion traces of the topological charges evolution process for 10 different relative positions.
-
[1] Crawford G P, Zumer S 1996 Liquid Crystals in Complex Geometries: Formed by Polymer and Porous Networks (CRC Press: Boca Raton) p521
[2] Takeuchi H, Tsubota M 2006 J. Phys. Soc. Jpn. 75 063601
Google Scholar
[3] Joyce D D 2000 Compact Manifolds with Special Holonomy (Oxford: Oxford University Press) p395.
[4] Dammone O J, Zacharoudiou I, Dullens R P, Yeomans J M, Lettinga M P, Aarts D G 2012 Phys. Rev. Lett. 109 108303
Google Scholar
[5] Duclos G, Adkins R, Banerjee D, Peterson M S E, Varghese M, Kolvin I, Baskaran A, Pelcovits R A, Powers T R, Baskaran A, Toschi F, Hagan M F, Streichan S J, Vitelli V, Beller D A, Dogic Z 2020 Science 367 1120
Google Scholar
[6] Manyuhina O V, Lawlor K B, Marchetti M C, Bowick M J 2015 Soft Matter 11 6099
Google Scholar
[7] Smalyukh I I, Lansac Y, Clark N A, Trivedi R P 2010 Nat. Mater. 9 139
Google Scholar
[8] Senyuk B, Liu Q, He S, Kamien R D, Kusner R B, Lubensky T C, Smalyukh Ⅱ 2013 Nature 493 200
Google Scholar
[9] 刘永军, 孙伟民, 刘晓颀, 姚丽双, 鲁兴海, 宣丽 2012 61 114211
Google Scholar
Liu Y J, Sun W M, Liu X Q, Yao L S, Lu X H, Xuan L 2012 Acta Phys. Sin. 61 114211
Google Scholar
[10] 吕月兰, 尹向宝, 杨月, 刘永军, 苑立波 2017 66 154205
Google Scholar
Lü Y L, Yin X B, Yang Y, Liu Y J, Yuan L B 2017 Acta Phys. Sin. 66 154205
Google Scholar
[11] Ackerman P J, van de Lagemaat J, Smalyukh Ⅱ 2015 Nat. Commun. 6 6012
Google Scholar
[12] Xing X, Shin H, Bowick M J, Yao Z, Jia L, Li M H 2012 Proc. Natl. Acad. Sci. U. S. A 109 5202
Google Scholar
[13] Opathalage A, Norton M M, Juniper M P N, Langeslay B, Aghvami S A, Fraden S, Dogic Z 2019 Proc. Natl. Acad. Sci. U. S. A. 116 4788
Google Scholar
[14] Dolganov P V, Cluzeau P, Dolganov V K 2019 Liq. Cryst. Rev. 7 1
Google Scholar
[15] Peng C, Lavrentovich O D 2019 Micromachines-Basel 10 02187
[16] Turiv T, Krieger J, Babakhanova G, Yu H, Shiyanovskii S V, Wei Q H, Kim M H, Lavrentovich O D 2020 Sci. Adv. 6 eaaz6485
Google Scholar
[17] Giomi L, Kos Z, Ravnik M, Sengupta A 2017 Proc. Natl. Acad. Sci. U. S. A. 11 4
[18] Liu Q, Senyuk B, Tasinkevych M, Smalyukh Ⅱ 2013 Proc. Natl. Acad. Sci. U. S. A. 110 9231
Google Scholar
[19] Solodkov N V, Shim J U, Jones J C 2019 Nat. Commun. 10 198
Google Scholar
[20] Liang D, Ma X, Liu Z, Jafri H M, Cao G, Huang H, Shi S, Chen L Q 2020 J. Appl. Phys. 128 124701
Google Scholar
[21] Tang X, Selinger J V 2017 Soft Matter 13 5481
Google Scholar
[22] De Gennes P G, Prost J 1993 The Physics of Liquid Crystals (Vol. 83) (New York: Oxford University Press) p597.
[23] Pelka R, Saito K 2006 Phys. Rev. E 74 041705
Google Scholar
[24] Frank F C 1958 Discuss. Faraday Soc. 25 19
Google Scholar
[25] Berreman D W, Meiboom S 1984 Phys. Rev. A 30 1955
Google Scholar
[26] Longa L, Monselesan D, Trebin H R 1987 Liq. Cryst. 2 769
Google Scholar
[27] Inukai T, Miyazawa K 1917 Outline of Development of Nematic Liquid Crystal Compounds for LCD (The Museum: King's Printer for British Columbia) p559.
[28] Fournier J B, Galatola P 2005 Europhys. Lett. 72 403
Google Scholar
[29] Duclos G, Erlenkämper C, Joanny J F, Silberzan P 2017 Nat. Phys. 13 58
Google Scholar
下载:
计量
- 文章访问数: 5754
- PDF下载量: 71
- 被引次数: 0
