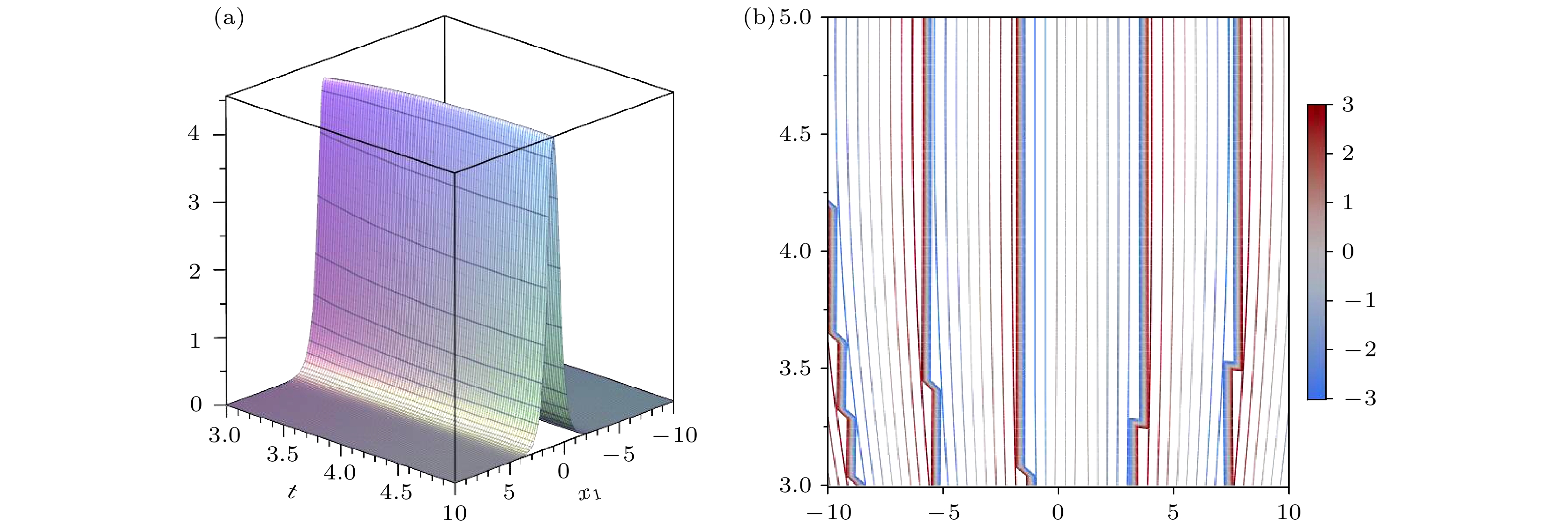
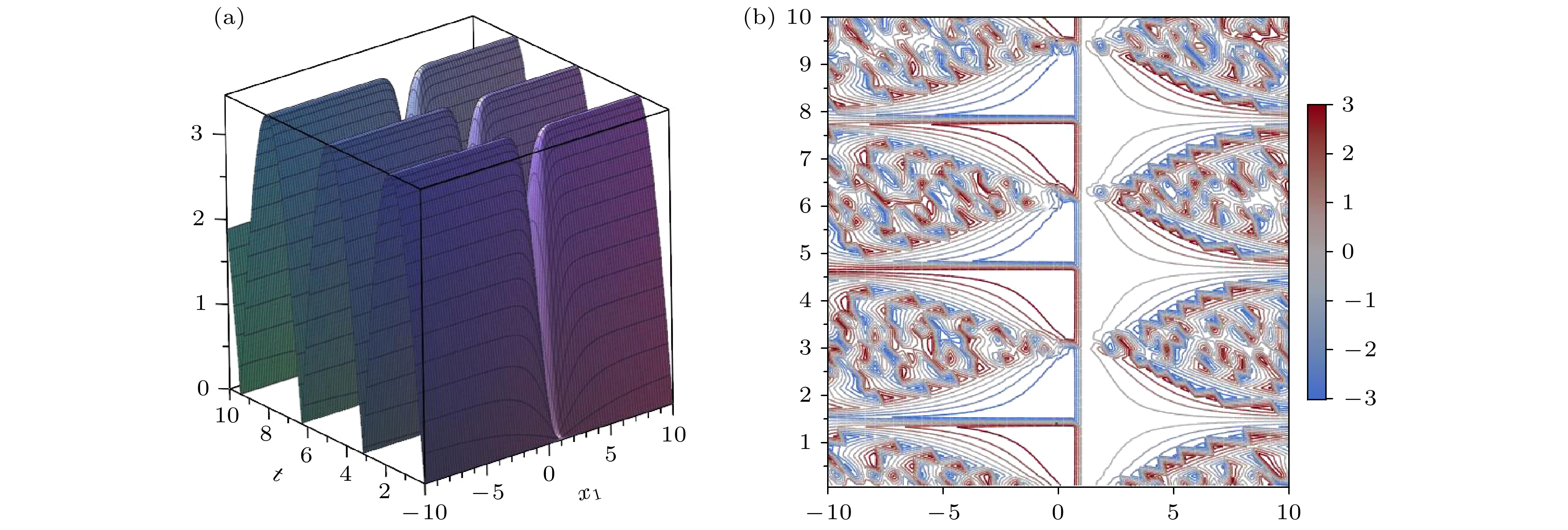
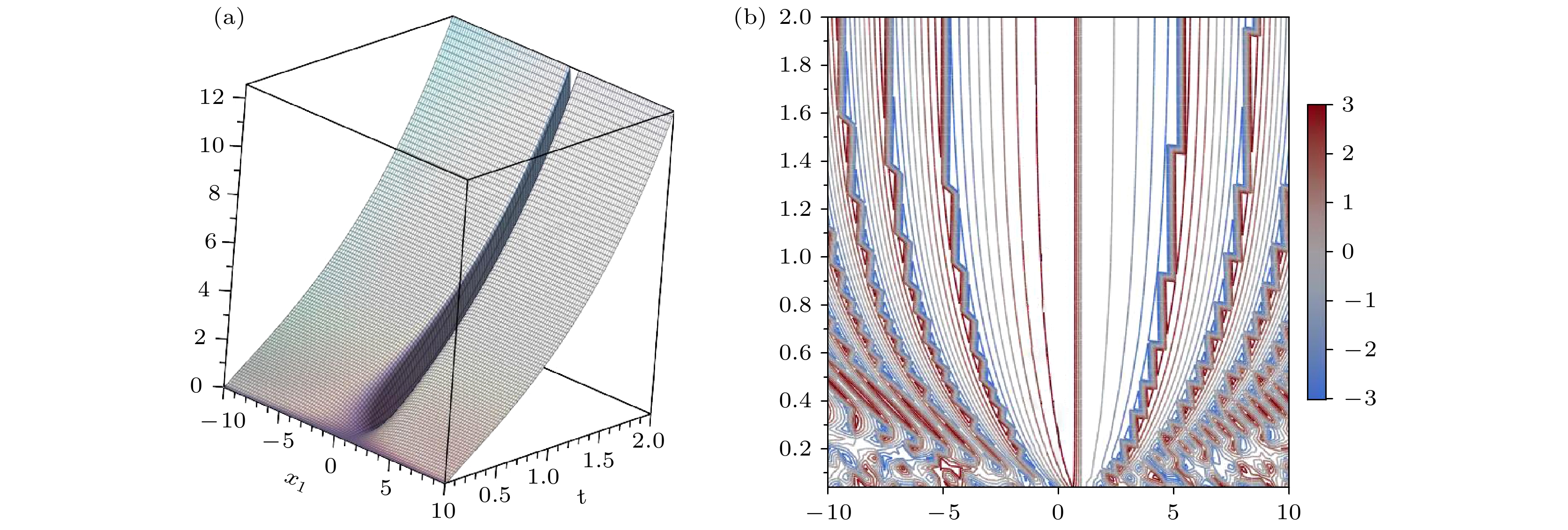
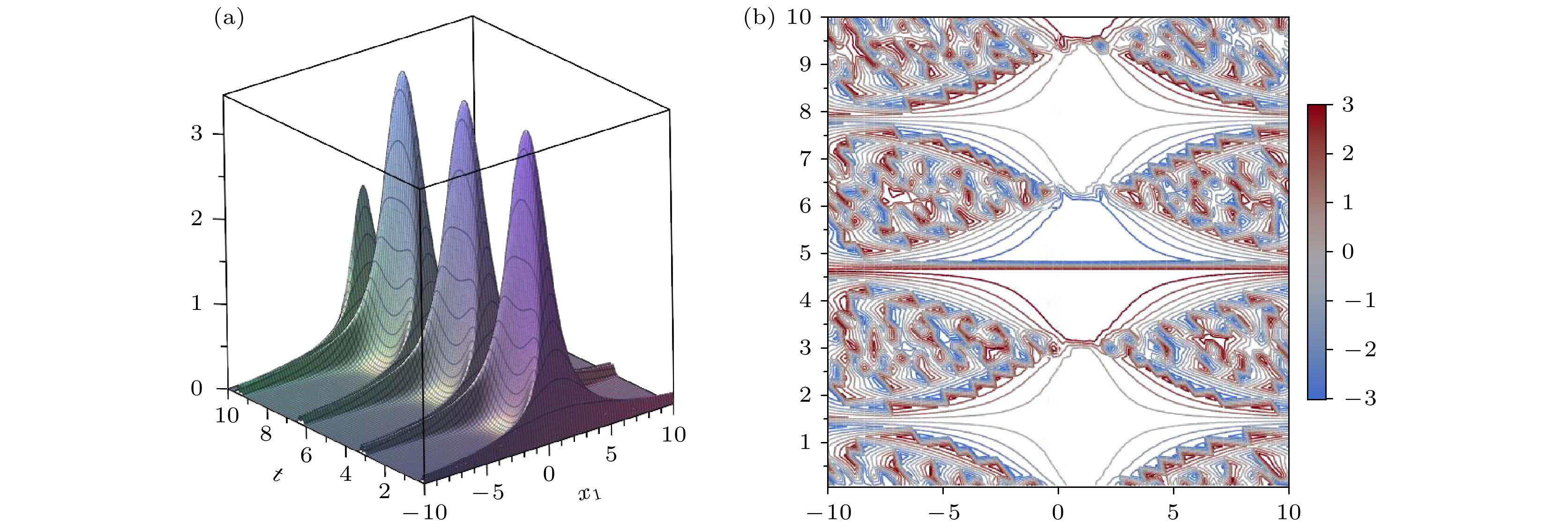
-
薛定谔型方程是一类十分重要的微分方程.高维及变系数薛定谔型方程的研究具有一定的价值和意义.本文利用相似变换推导了（n+1）维（2m+1）次变系数非线性薛定谔方程的一类新的孤子解，给出了系数之间满足的关系.并利用定态薛定谔方程的解，得到了（n+1）维（2m+1）次变系数非线性薛定谔方程的明暗孤子解.最后，对于特殊的情况，给出了明暗孤立子解的图像，并系统分析了孤子解的空间结构和传播特性.
-
关键词:
- （n+1）维（2m+1）次非线性薛定谔方程 /
- 相似变换 /
- 精确解
Schrödinger-type equations represent a fundamentally important class of differential equations. The study of high-dimensional and variable-coeffcient Schrödingertype equations is of significant theoretical and practical value, providing critical insights into the dynamics of complex wave phenomena. In this paper, we employ similarity transformations to derive a novel class of soliton solutions for the (n + 1)-dimensional (2m + 1) th-order variable-coeffcient nonlinear Schrödinger equation. By extending similarity transformations from lower-dimensional equations to higher dimensions, we establish the intrinsic relationships among the equation’ s coeffcients. Furthermore, utilizing the solutions of the stationary Schrödinger equation and applying the balancing-coeffcient method, we construct both bright and dark soliton solutions for the (n+1)-dimensional (2m+1) th-order variable-coeffcient nonlinear Schrödinger equation. Finally, for specific cases, we present graphical representations of the bright and dark soliton solutions and conduct a systematic analysis of their spatial structures and propagation characteristics. Our results reveal that bright solitons exhibit a single-peak structure, while dark solitons form trough-like profiles, further confirming the stability of soliton wave propagation.-
Keywords:
- (n + 1)-dimensional (2m + 1)-th nonlinear Schrödinger equation /
- Similarity transformations /
- Exact solutions
-
[1] Zhong M, Malomed B A, Yan Z 2024 Phys. Rev. E 110014215
[2] Malomed B A 2024 Chaos (Woodbury, N.Y.) 34022102
[3] Kudryashov N A, Nifontov D R, Biswas A 2024 Phys. Lett. A 528130037
[4] Wang T Y, Zhou Q, Liu W J 2022 Chin. Phys. B 31020501
[5] Lü X, Zhu H W, Yao Z Z, Meng X H, Zhang C, Zhang C Y, Tian B 2008 Ann. Phys. 323194755
[6] Gong R Z, Wang D S 2023 Acta Phys. Sin. 72100503(in Chinese)（公睿智, 王灯山2023 72100503）
[7] Pérez-García V M, Pardo R 2009 Physica D 238135261
[8] Dinh V D. 2022 Nonlinear Anal. 214112587
[9] Rizvi S T R, Seadawy A R, Farah N, Ahmad S 2022 Chaos, Solitons Fractals 159112128
[10] Yang Z, Zhong W P, Belić, M R 2023 Phys. Lett. A 465128715
[11] Djelah G, Ndzana F I I, Abdoulkary S, English L Q, Mohamadou A 2024 Phys. Lett. A 518129666
[12] Rao J G, Chen S A, Wu Z J, He J S 2023 Acta Phys. Sin. 72104204(in Chinese) (饶继光, 陈生安, 吴昭君, 贺劲松2023 72104204)
[13] Sun B, Zhao L C, Liu J 2023 Acta Phys. Sin. 72100501(in Chinese) (孙斌, 赵立臣, 刘杰 2023 72100501)
[14] Pei Y T, Wang J K, Guo B L, Liu W M 2023 Acta Phys. Sin. 72100201(in Chinese) (裴一潼, 王锦坤, 郭柏灵, 刘伍明2023 72100201)
[15] Wen J M, Bo W B, Wen X K, Dai C Q 2023 Acta Phys. Sin. 72100502(in Chinese) (温嘉美, 薄文博, 温学坤, 戴朝卿2023 72100502)
[16] Lou S Y, Hao X Z, Jia M 2023 Acta Phys. Sin. 72100204(in Chinese) (楼森岳, 郝夏芝, 贾曼2023 72100204)
[17] Rao J, Mihalache D, Ma M, He J 2024 Phys. Lett. A 493129244
[18] Yang J Q, Liu W J 2023 Acta Phys. Sin. 72100504(in Chinese) (杨佳奇, 刘文军2023 72100504)
[19] Liao Q Y, Hu H J, Chen M W, Shi Y, Zhao Y, Hua C B, Xu S L, Fu Q D, Ye F W, Zhou Q 2023 Acta Phys. Sin. 72104202(in Chinese) (廖秋雨, 胡恒洁, 陈懋薇, 石逸, 赵元, 花春波, 徐四六, 傅其栋, 叶芳伟, 周勤2023 72104202)
[20] Wang G 2016 Appl. Math. Lett. 565664
[21] Zhang J, Wang G 2025 Appl. Math. Lett. 159109286
计量
- 文章访问数: 116
- PDF下载量: 7
- 被引次数: 0
下载:
