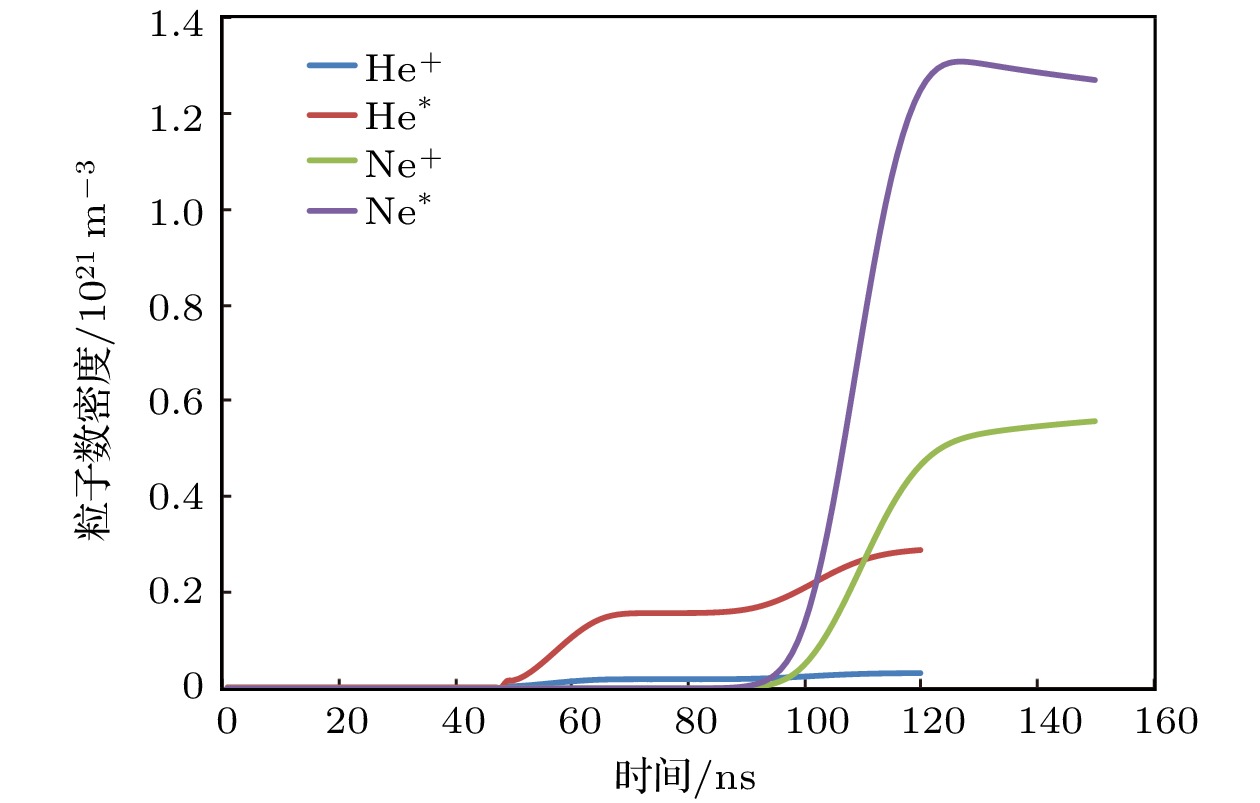
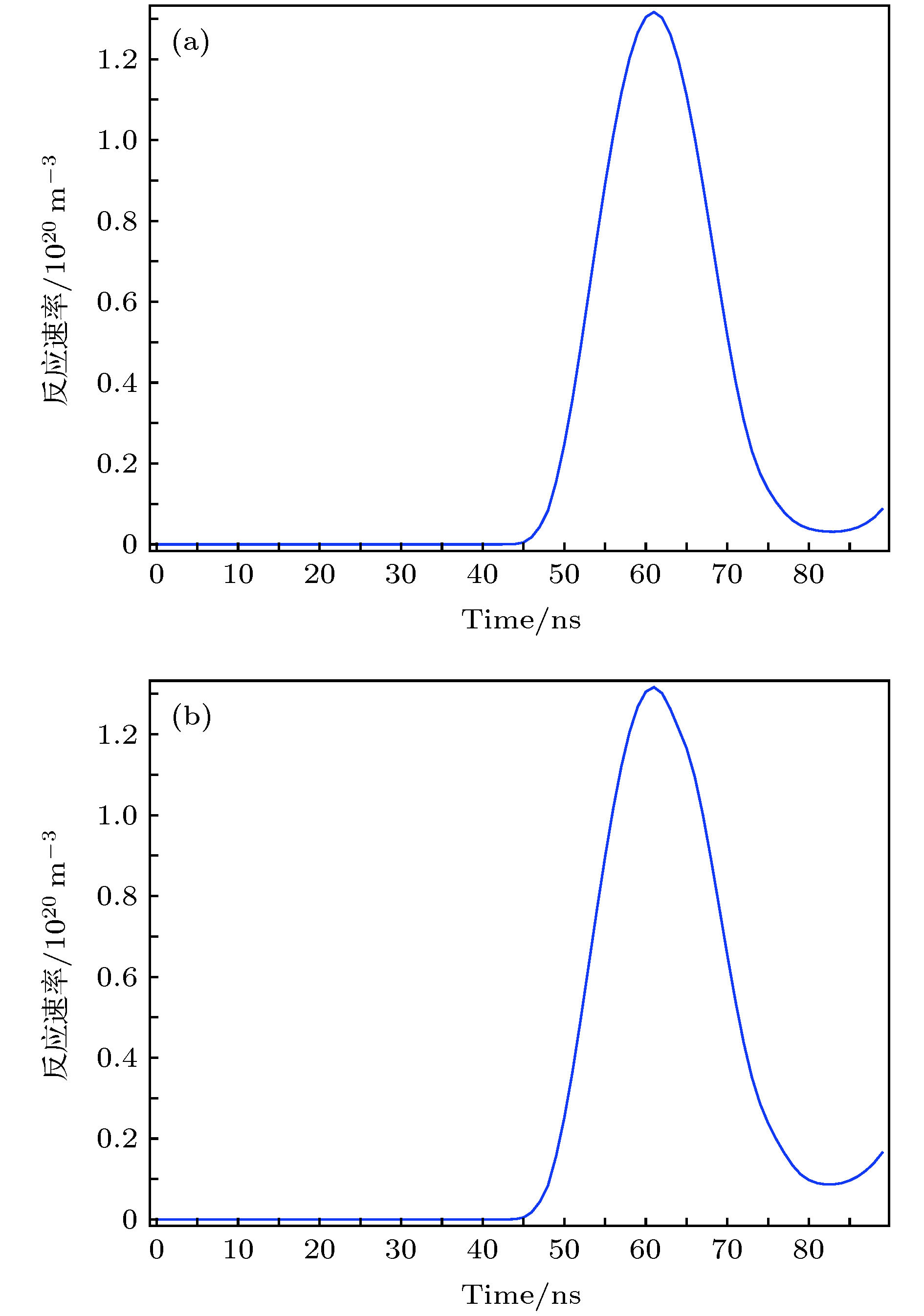
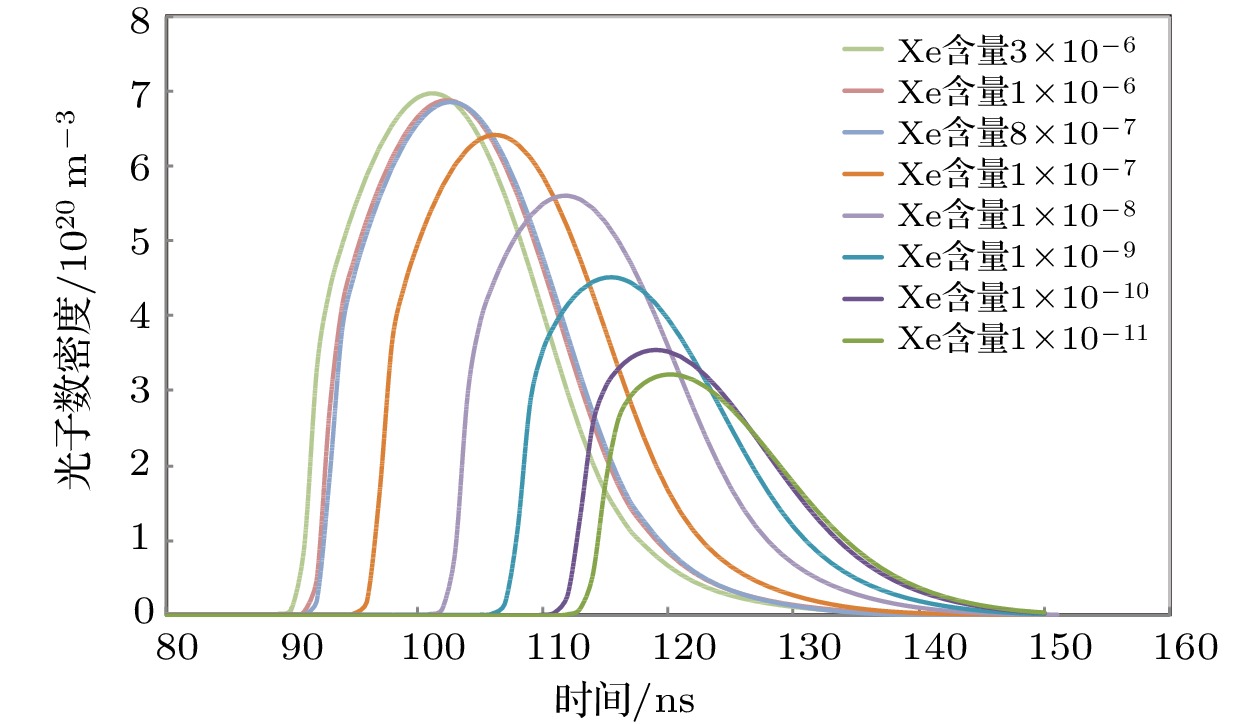
-
为深入理解挖掘ArF准分子激光系统运转机制, 进而获得ArF准分子激光系统设计优化的理论及方向性指导, 文章基于流体模型, 以气体高压放电等离子体深紫外激光辐射过程为主要研究对象, 研究了放电抽运ArF准分子激光系统的动力学特性, 分析了不同缓冲气体中, ArF准分子激光系统极板间电压、电流、光子数密度变化趋势及电子数密度空间分布情况, 讨论了光电离在系统放电过程中的重要作用. 结果表明, Ne作为缓冲气体时, 电子耗尽层及阴极鞘层宽度更小, 放电更加稳定. 在Ne中添加杂质气体Xe, 可以通过光电离加速放电区域的扩展, 减小电子耗尽层及阴极鞘层的宽度, 降低放电发生的阈值电压, 提高放电稳定性.Excimer laser is the current mainstream source of international semiconductor lithography. The stable operation of the laser system directly affects the working efficiency of the semiconductor lithography machine, so it is very important to optimize the laser system. The buffer gas commonly used in ArF excimer laser systems is He, Ne. In the early years, Shinjin Nagai and Mieko Ohwa have studied the output characteristics of the system when using He or Ne as a buffer gas from the aspect of pump efficiency and gain coefficient, and pointed out that using Ne instead of He has no obvious advantages in terms of efficiency. However, when Ne is used as the buffer gas, the reaction between Ne and electrons is more complicated. In addition to direct ionization and excitation reactions, it also contains a large amount of step ionization and secondary ionization, which releases free electrons. The stability of the system is improved, when Ne is used as the buffer gas. The ArF excimer laser system discharge characteristics in different buffer gases are analyzed based on fluid model in the paper. The role of photoionization is discussed. The simulation results show that the width of the electron depletion layer and the cathode sheath are both smaller, and the discharge stability is higher when Ne is used as the buffer gas. The expansion of the discharge region is accelerated and the threshold voltage of the discharge is reduced by adding Xe into Ne to trigger photoionization. The excimer laser discharge process is very complicated and is affected by many factors. Only two factors of the buffer gas and the photoionization process are studied in this paper. The simulation model will be extended from one-dimensional case to two-dimensional case in the future, and multiple physical factors of the ArF excimer laser system will be considered.
-
Keywords:
- ArF excimer laser /
- fluid model /
- electron density /
- photoionization
[1] Vladimir F, Slava R, Robert B, Hong Y, Kevin O, Robert J, Fedor T, Efrain F, Theodore C, Daniel B, William P 2008 Proc. SPIE 6924 69241R
Google Scholar
[2] Hirotaka M, Takahito K, Hiroaki T, Akihiko K, Takeshi O, Takashi M, Hakaru M 2016 Proc. SPIE 7980 79801I
[3] Hirotaka M, Hiroshi F, Keisuke I, Hiroaki T, Akihiko K, Hiroshi T, Takeshi O, Satoru B, Takashi S, Hakaru M 2018 Proc. SPIE 10587 1058710
[4] Mieko O, Minoru O 1986 J. Appl. Phys. 59 32
Google Scholar
[5] Shinji N, Hideo F, Yoshiyuki U, Jun Y, Akihiro K, Toshio G 1995 J. Appl. Phys. 77 2906
Google Scholar
[6] Mieko O, Minoru O 1988 J. Appl. Phys. 63 1306
Google Scholar
[7] Jiang C, Wang Y Q 2006 Plasma Sci. Technol. 8 185
Google Scholar
[8] 石锋 2008 硕士学位论文(大连: 大连理工大学)
Shi F 2008 M. S. Dissertation (Da Lian: Dalian University of Technology) (in Chinese)
[9] Yang C G, Duan L, Xu Y Y, Wang X B, Zuo D L 2012 Phys. Plasma. 19 093510
Google Scholar
[10] 罗时文, 左都罗, 王新兵 2015 强激光与粒子束 27 081006
Google Scholar
Luo S W, Zuo D L, Wang X B 2015 High Power Laser and Particle Beams 27 081006
Google Scholar
[11] 王倩, 赵江山, 罗时文, 左都罗, 周翊 2016 65 214205
Google Scholar
Wang Q, Zhao J S, Luo S W, Zuo D L, Zhou Y 2016 Acta Phys. Sin. 65 214205
Google Scholar
[12] Thomos H J, Louis J P, Allen M H 1979 IEEE J. Quantum Electron. 15 289
Google Scholar
[13] Kulikovsky A A 1994 J. Phys. D: Appl. Phys. 27 2556
Google Scholar
[14] Akashi H, Sakai Y, Tagashira H 1994 J. Phys D: Appl Phys. 27 1097
Google Scholar
[15] Akashi H, Sakai Y, Tagashira H 1995 J. Phys. D: Appl. Phys. 28 445
Google Scholar
[16] Rauf S, Kushner M J 1999 J. Appl. Phys. 85 3460
Google Scholar
[17] Razhev A M, Shchedrin A M, Kalyuzhnaya A G, Zhupikov A A 2005 Quantum Electron. 35 799
Google Scholar
[18] Xiong Z, Kushner M J 2011 J. Appl. Phys. 110 083304
Google Scholar
[19] Levatter J I, Lin S C 1980 J. Appl. Phys. 51 210
Google Scholar
-
图 3 极板间电压、电流及光子数密度随时间变化图(He为缓冲气体)
Fig. 3. Waveforms of discharge voltage, current, and photon number density (He is the buffer gas).
图 4 极板间电压、电流及光子数密度随时间变化图(Ne为缓冲气体)
Fig. 4. Waveforms of discharge voltage, current, and photon number density (Ne is the buffer gas).
图 5 电子数密度空间分布 (a) He作为缓冲气体; (b) Ne作为缓冲气体
Fig. 5. Electron number density spatial distribution: (a) He as the buffer gas; (b) Ne as the buffer gas.
图 7 距离阴极0.2 cm处, 电子数密度随时间分布 (a) 不考虑光电离; (b)考虑光电离
Fig. 7. Waveforms of electron number density at 0.2 cm from cathode: (a) Considering photoionization; (b) without photoionization.
图 8 添加Xe与不添加Xe极板间电流、电压及光子数密度变化图
Fig. 8. Waveforms of discharge voltage, current, and photon number density with and without Xe.
图 9 添加Xe后电子数密度空间分布
Fig. 9. Waveforms of electron number density spatial distribution with Xe.
图 10 不同Xe含量光子数密度分布情况
Fig. 10. Waveforms of photon number density with different Xe ratios.
表 1 ArF准分子激光器等离子反应过程(He作为缓冲气体)
Table 1. Plasma reaction process of ArF excimer laser system (He is the buffer gas).
反应类型 反应过程 反应系数 参考文献 电子碰撞反应 Ar + e → Ar+ + 2e 计算玻尔兹曼方程得到 Ar + e → Arex + e 计算玻尔兹曼方程得到 Ar + e → Ar* + e 计算玻尔兹曼方程得到 Ar* + e → Ar+ + 2e 计算玻尔兹曼方程得到 F2 + e → F– + F 计算玻尔兹曼方程得到 He + e → He+ + 2e 计算玻尔兹曼方程得到 He + e → Heex + e 计算玻尔兹曼方程得到 He + e → He* + e 计算玻尔兹曼方程得到 中性粒子反应 Ar+ + 2 Ar → Ar2+ + Ar 2.5 × 10–31 cm6·s–1 [15] Ar+ + F– → ArF* 1 × 10–6 cm3·s–1 [15] Ar2+ + F–→ ArF* + Ar 1 × 10–6 cm3·s–1 [15] Arex → Ar + hγ’ 1.0 ns [15] Ar* + F2 → ArF* + F 8 × 10–10 cm3·s–1 [15] ArF*→Ar + F + hγ 42 ns [15] 受激辐射 ArF* + hγ → ArF + 2hγ 4 × 10–16 cm3·s–1 [15] 光电离 hγ + F– → F + e 1 × 10–17 cm3 [15] Arex + hγ → Ar+ + e 1 × 10–18 cm3 [15] 
下载: 导出CSV
表 2 ArF准分子激光器等离子反应过程(Ne作为缓冲气体)
Table 2. Plasma reaction process of ArF excimer laser system (Ne is buffer gas).
反应类型 反应过程 反应系数 参考文献 电子碰撞反应 Ar + e → Ar+ + 2e 计算玻尔兹曼方程得到 Ar + e → Arex + e 计算玻尔兹曼方程得到 Ar + e → Ar* + e 计算玻尔兹曼方程得到 Ar* + e → Ar+ + 2e 计算玻尔兹曼方程得到 F2 + e → F – + F 计算玻尔兹曼方程得到 Ne* + e → Ne+ + 2e 计算玻尔兹曼方程得到 Ne + e → Ne+ + 2e 计算玻尔兹曼方程得到 Ne + e → Ne* + e 计算玻尔兹曼方程得到 中性粒子反应 Ne2* + e → 2e + Ne2+ (9.75 × 10–9) × (abs(Te))0.71 × exp(–3.4/abs(Te)) [16] Ne2+ + e → Ne* + Ne (3.7 × 10–8) × (abs(Te))–0.43 [16] Ar+ + 2Ar → Ar2+ + Ar 2.5 × 10–31 cm6·s–1 [15] Ar+ + F– → ArF* 1 × 10–6 cm3·s–1 [15] Ar2+ + F– → ArF* + Ar 1 × 10–6 cm3·s–1 [15] Arex → Ar + hγ’ 1.0 ns [15] Ar* + F2 → ArF* + F 8 × 10–10 cm3·s–1 [15] 2Ne* → Ne+ + Ne + e 5 × 10–10 cm3·s–1 [17] Ne+ + 2Ne →Ne2+ + Ne 4.4 × 10–32 cm6·s–1 [17] Ne* + Ne + Ne → Ne2* + Ne 4 × 10–34 cm6·s–1 [17] Ar + ArF* → 2Ar + F 9 e × 10-12 cm3·s–1 [15] Ne + ArF* → Ar + Ne + F 1 × 10–12 cm3·s–1 [17] F2 + ArF* → Ar + 3F 1.9 × 10–9 cm3·s–1 [15] 受激辐射 ArF* + hγ → ArF + 2hγ 4 × 10–16 cm3·s–1 [15] 光电离 hγ + F– → F + e 1 × 10–17 cm3 [15] Arex + hγ → Ar+ + e 1 × 10–18 cm3 [15] Xe + hγ’→Xe+ + e 阈值为 12.1 eV, 截面为1 × 10–16 cm2 [18]
下载: 导出CSV
-
[1] Vladimir F, Slava R, Robert B, Hong Y, Kevin O, Robert J, Fedor T, Efrain F, Theodore C, Daniel B, William P 2008 Proc. SPIE 6924 69241R
Google Scholar
[2] Hirotaka M, Takahito K, Hiroaki T, Akihiko K, Takeshi O, Takashi M, Hakaru M 2016 Proc. SPIE 7980 79801I
[3] Hirotaka M, Hiroshi F, Keisuke I, Hiroaki T, Akihiko K, Hiroshi T, Takeshi O, Satoru B, Takashi S, Hakaru M 2018 Proc. SPIE 10587 1058710
[4] Mieko O, Minoru O 1986 J. Appl. Phys. 59 32
Google Scholar
[5] Shinji N, Hideo F, Yoshiyuki U, Jun Y, Akihiro K, Toshio G 1995 J. Appl. Phys. 77 2906
Google Scholar
[6] Mieko O, Minoru O 1988 J. Appl. Phys. 63 1306
Google Scholar
[7] Jiang C, Wang Y Q 2006 Plasma Sci. Technol. 8 185
Google Scholar
[8] 石锋 2008 硕士学位论文(大连: 大连理工大学)
Shi F 2008 M. S. Dissertation (Da Lian: Dalian University of Technology) (in Chinese)
[9] Yang C G, Duan L, Xu Y Y, Wang X B, Zuo D L 2012 Phys. Plasma. 19 093510
Google Scholar
[10] 罗时文, 左都罗, 王新兵 2015 强激光与粒子束 27 081006
Google Scholar
Luo S W, Zuo D L, Wang X B 2015 High Power Laser and Particle Beams 27 081006
Google Scholar
[11] 王倩, 赵江山, 罗时文, 左都罗, 周翊 2016 65 214205
Google Scholar
Wang Q, Zhao J S, Luo S W, Zuo D L, Zhou Y 2016 Acta Phys. Sin. 65 214205
Google Scholar
[12] Thomos H J, Louis J P, Allen M H 1979 IEEE J. Quantum Electron. 15 289
Google Scholar
[13] Kulikovsky A A 1994 J. Phys. D: Appl. Phys. 27 2556
Google Scholar
[14] Akashi H, Sakai Y, Tagashira H 1994 J. Phys D: Appl Phys. 27 1097
Google Scholar
[15] Akashi H, Sakai Y, Tagashira H 1995 J. Phys. D: Appl. Phys. 28 445
Google Scholar
[16] Rauf S, Kushner M J 1999 J. Appl. Phys. 85 3460
Google Scholar
[17] Razhev A M, Shchedrin A M, Kalyuzhnaya A G, Zhupikov A A 2005 Quantum Electron. 35 799
Google Scholar
[18] Xiong Z, Kushner M J 2011 J. Appl. Phys. 110 083304
Google Scholar
[19] Levatter J I, Lin S C 1980 J. Appl. Phys. 51 210
Google Scholar
下载:
计量
- 文章访问数: 6938
- PDF下载量: 81
- 被引次数: 0
