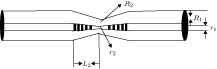
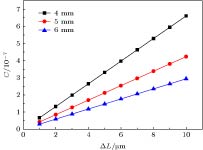
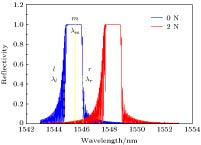
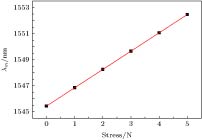
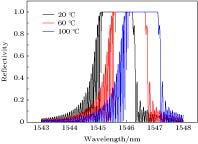
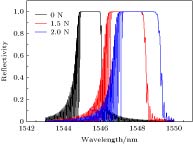
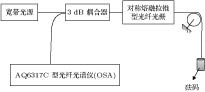
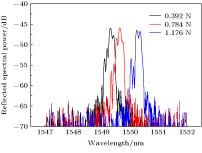
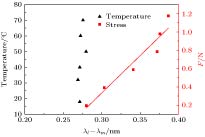
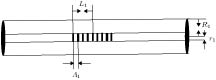
-
锥形结构的光纤光栅具有对应力敏感而对温度不敏感的特性, 这可以有效抑制温度与应力的交叉敏感问题. 提出一种利用熔融拉锥技术实现对称双锥形结构的光纤光栅, 结合传输矩阵法建立其传感特性理论模型并加以分析. 首先研究影响啁啾系数变化的因素, 得到啁啾系数与光栅长度变化量的关系; 其次对对称熔融拉锥型光纤光栅的光谱特性进行分析, 讨论光谱短波长处出现密集调制现象的成因; 然后仿真研究温度和应力对对称熔融拉锥型光纤光栅的反射谱影响, 得到对应的中心波长和光谱宽度的变化关系. 并针对应力灵敏度较低问题, 提出聚合物涂覆锥区增大传感锥区光纤半径差而进行增敏的方案, 利用熔融拉锥法制备对称熔融型光纤光栅, 通过实验验证理论仿真的正确性, 对称熔融拉锥型光纤光栅应力灵敏度为0.11391 nm/N. 研究表明, 对称熔融拉锥型光纤光栅的啁啾系数与光栅长度变化量满足线性关系. 对称熔融拉锥型光纤光栅端处光栅周期较小, 且反射率小于1, 左边透射光与右边反射光会产生干涉, 因此光谱短波长处会出现密集调制现象. 随着轴向应力的增大, 光栅反射中心波长向长波方向移动, 光谱宽度变大, 且两者与轴向应力均满足线性关系; 随着温度升高, 反射谱峰中心波长向长波方向移动, 满足线性关系, 而温度对光谱宽度的影响可忽略不计. 通过增大传感锥区光纤光栅半径差, 光纤光栅的应力灵敏度较之前提高了数百倍, 并且增大光栅长度变化量有助于进一步提高应力灵敏度. 对称熔融拉锥型光纤光栅的光谱宽度只对应力敏感而对温度不敏感, 这一特性可用于实现温度与应力双参量测量.The stress-sensitive and temperature-insensitive characteristics of the tapered fiber grating can be used effectively to suppress the cross-sensitive problem of temperature and stress. In this paper, a fiber grating with a symmetric double-cone shape is proposed, which is made by using a fused taper technology. The theoretical model of sensing characteristics is established and analyzed by the transfer matrix method. Firstly, the factors affecting the change of radon coefficient are studied, and the relationship between the radon coefficient and the amount of grate length change is obtained, and then the spectral characteristics of the symmetric fused-tapered fiber grating are analyzed to discuss the origin of dense modulation at the short wavelength of the spectrum. The effects of temperature and stress on the reflection spectrum of symmetrically fused-tapered fiber grating are studied, and the relationship between the corresponding center wavelength and spectral bandwidth is obtained. In order to solve the problem of low stress sensitivity of the fiber grating, a scheme is presented that the radius difference of the optical fiber in the sensing cone region is enhanced by using polymer to coat the tapered area. Finally, a fused taper technology is used to prepare the symmetrically molten fiber grating, and verify the correctness of theoretical simulation in experiment, indicating that its stress sensitivity is 0.11391 nm/N. Firstly, the ripple coefficient of the symmetrically fused-tapered fiber grating is linearly related to the amount of change in the length of the grating. Secondly, because the grating cycle is small at the end of the symmetrically melt-pull-cone fiber-optic grating, and the reflectivity is less than 1, the left-hand transmission light and the right-hand reflected light will produce interference, so the spectral short wavelength will present dense modulation phenomenon. Thirdly, the center wavelength shifts to long wavelength region and the reflection bandwidth is broadened as stress is raised, and the center wavelength and reflection bandwidth are both linearly changed with the applied stress. Finally, the center wavelength shifts to long wavelength region as the temperature rises gradually, and the effect on the spectral bandwidth can be ignored. The stress sensitivity of the fiber grating increases hundreds of times by increasing the difference in fiber optic grating radius in the sensing tapered area, and the stress sensitivity can be further improved by increasing the fused taper variation of the grating. The spectral bandwidth of the symmetrical fused tapered fiber grating is only sensitive to stress but not to temperature. The characteristics can be used to realize the double-parameter measurement of temperature and stress.
-
Keywords:
- tapered fiber grating /
- fused-biconical taper /
- effective index /
- grating period /
- sensing
[1] 芦吉云, 梁大开, 张晓丽, 朱珠 2009 光谱学与光谱分析 29 3429
Google Scholar
Lu G Y, Liang D K, Zhang X L, Zhu Z 2009 Spectrosc. Spectr. Anal. 29 3429
Google Scholar
[2] Zhao X W, Wang Q 2019 Instrum. Sci. Technol. 47 140
Google Scholar
[3] 张敬花, 乔学光, 冯忠耀, 忽满利, 高宏, 周锐, 杨扬 2012 61 054215
Google Scholar
Zhang J H, Qiao X G, Feng Z Y, Hu M L, Gao H, Zhou R, Yang Y 2012 Acta Phys. Sin. 61 054215
Google Scholar
[4] Zhao L J 2011 M. S. Thesis (Wuxi: Jiangnan University) (in Chinese)
[5] Geng S G 2017 M. S. Thesis (Nanjing: Nanjing University of Posts and Telecommunications) (in Chinese)
[6] Xu M G, Archambault J L, Reekie L, Dakin J P 1994 Electron. Lett. 30 1085
Google Scholar
[7] James S W, Dockney M L, Tatam R P 1996 Electron. Lett. 32 1133
Google Scholar
[8] Meng A H 2017 M. S. Thesis (Changchun: Jilin University) (in Chinese)
[9] Huo W H 2018 M. S. Thesis (Beijing: Beijing Jiaotong University) (in Chinese)
[10] 尹彬, 柏云龙, 齐艳辉, 冯素春, 简水生 2013 62 214213
Google Scholar
Yin B, Bai Y L, Qi Y H, Feng S C, Jian S S 2013 Acta Phys. Sin. 62 214213
Google Scholar
[11] Jiao S X, Zhao Y, Gu J J 2018 Instrum. Sci. Technol. 46 463
Google Scholar
[12] Putnam M A, Williams G L M, Friebele E J 1995 Electron. Lett. 31 309
Google Scholar
[13] 杨先辉, 于永森, 张秋华, 孙圣和 2007 光电子·激光 18 600
Google Scholar
Yang X H, Yu Y S, Zhang Q H, Sun S H 2007 J. Optoe. Laser. 18 600
Google Scholar
[14] Qiu S, Chen Y, Kou J 2011 Appl. Opt. 50 4328
Google Scholar
[15] Yoon M S, Park S, Han Y G 2012 J. Lightwave Technol. 30 1156
Google Scholar
[16] Osuch T 2016 Opt. Commun. 366 194
Google Scholar
[17] Zhang B, Kahrizi M 2007 IEEE Sens. J. 7 586
Google Scholar
[18] 王涛, 何大伟, 王永生, 全雨, 王鹏飞, 尹泽霖 2013 光谱学与光谱分析 33 1411
Google Scholar
Wang T, He D W, Wang Y S, Quan Y, Wang P F, Yin Z L 2013 Spectrosc. Spectr. Anal. 33 1411
Google Scholar
[19] 刘学静, 杨远洪, 张晓哲, 靳伟 2013 中国激光 40 0505002
Liu X J, Yang H Y, Zhang X Z, Jin W 2013 Chin. J. Lasers. 40 0505002
[20] Bandyopadhyay S, Canning J, Stevenson M, Cook K 2008 Opt. Lett. 33 1917
Google Scholar
[21] Markowski K, Jedrzejewski K, Osuch T 2016 Appl. Opt. 55 4505
Google Scholar
[22] Silva S F O, Ferreira L A, Araújo F M, Santos J L, Frazão O 2011 Fiber Integr.Opt. 30 9
Google Scholar
[23] Zhuo Z C, Ham B S 2009 Opt. Fiber Technol. 15 442
Google Scholar
[24] 曹后俊, 司金海, 陈涛, 王瑞泽, 高博, 闫理贺, 侯洵 2018 中国激光 45 0702009
Cao H J, Si J H, Chen T, Wang R Z, Gao B, Yan L H, Hou X 2018 Chin. J. Lasers. 45 0702009
-
图 3 啁啾系数随锥区长度及其变化量分布图
Fig. 3. Distribution of the chirp coefficient with the length of the cone and its variation.
图 4 光栅长度变化量1 μm的反射光谱图
Fig. 4. Reflectance spectra with the grating length variation of 1 μm.
图 6 光谱带宽半宽度随轴向应力变化分布图
Fig. 6. Distribution of half-width of the spectral bandwidth with axial stress
图 7 光纤光栅在不同温度下的反射谱
Fig. 7. Reflection spectra of fiber grating at different temperatures.
图 8 光谱带宽半宽度随温度变化分布图
Fig. 8. Distribution of spectral bandwidth half-width with temperature
图 9 对称熔融拉锥型光纤光栅涂覆聚合物后结构图
Fig. 9. Symmetric fused-tapered fiber grating coated polymer structure.
图 10 增敏后的光纤光栅在不同应力下的反射谱
Fig. 10. Reflection spectra of sensitized fiber grating under different stresses
图 11 光谱带宽半宽度随轴向应力变化分布图
Fig. 11. Distribution of half-width of the spectral bandwidth with axial stress
图 13 光纤光栅在不同轴向应力下的光谱图
Fig. 13. Spectral diagram of fiber grating under different axial stresses.
图 14 光纤光栅在不同温度下的反射谱
Fig. 14. Reflective spectra of fiber grating at different temperatures.
图 15 温度与应力对
$\lambda _l - \lambda _m$ 的影响Fig. 15. Effects of temperature and stress on
$\lambda _l - \lambda _m$ . -
[1] 芦吉云, 梁大开, 张晓丽, 朱珠 2009 光谱学与光谱分析 29 3429
Google Scholar
Lu G Y, Liang D K, Zhang X L, Zhu Z 2009 Spectrosc. Spectr. Anal. 29 3429
Google Scholar
[2] Zhao X W, Wang Q 2019 Instrum. Sci. Technol. 47 140
Google Scholar
[3] 张敬花, 乔学光, 冯忠耀, 忽满利, 高宏, 周锐, 杨扬 2012 61 054215
Google Scholar
Zhang J H, Qiao X G, Feng Z Y, Hu M L, Gao H, Zhou R, Yang Y 2012 Acta Phys. Sin. 61 054215
Google Scholar
[4] Zhao L J 2011 M. S. Thesis (Wuxi: Jiangnan University) (in Chinese)
[5] Geng S G 2017 M. S. Thesis (Nanjing: Nanjing University of Posts and Telecommunications) (in Chinese)
[6] Xu M G, Archambault J L, Reekie L, Dakin J P 1994 Electron. Lett. 30 1085
Google Scholar
[7] James S W, Dockney M L, Tatam R P 1996 Electron. Lett. 32 1133
Google Scholar
[8] Meng A H 2017 M. S. Thesis (Changchun: Jilin University) (in Chinese)
[9] Huo W H 2018 M. S. Thesis (Beijing: Beijing Jiaotong University) (in Chinese)
[10] 尹彬, 柏云龙, 齐艳辉, 冯素春, 简水生 2013 62 214213
Google Scholar
Yin B, Bai Y L, Qi Y H, Feng S C, Jian S S 2013 Acta Phys. Sin. 62 214213
Google Scholar
[11] Jiao S X, Zhao Y, Gu J J 2018 Instrum. Sci. Technol. 46 463
Google Scholar
[12] Putnam M A, Williams G L M, Friebele E J 1995 Electron. Lett. 31 309
Google Scholar
[13] 杨先辉, 于永森, 张秋华, 孙圣和 2007 光电子·激光 18 600
Google Scholar
Yang X H, Yu Y S, Zhang Q H, Sun S H 2007 J. Optoe. Laser. 18 600
Google Scholar
[14] Qiu S, Chen Y, Kou J 2011 Appl. Opt. 50 4328
Google Scholar
[15] Yoon M S, Park S, Han Y G 2012 J. Lightwave Technol. 30 1156
Google Scholar
[16] Osuch T 2016 Opt. Commun. 366 194
Google Scholar
[17] Zhang B, Kahrizi M 2007 IEEE Sens. J. 7 586
Google Scholar
[18] 王涛, 何大伟, 王永生, 全雨, 王鹏飞, 尹泽霖 2013 光谱学与光谱分析 33 1411
Google Scholar
Wang T, He D W, Wang Y S, Quan Y, Wang P F, Yin Z L 2013 Spectrosc. Spectr. Anal. 33 1411
Google Scholar
[19] 刘学静, 杨远洪, 张晓哲, 靳伟 2013 中国激光 40 0505002
Liu X J, Yang H Y, Zhang X Z, Jin W 2013 Chin. J. Lasers. 40 0505002
[20] Bandyopadhyay S, Canning J, Stevenson M, Cook K 2008 Opt. Lett. 33 1917
Google Scholar
[21] Markowski K, Jedrzejewski K, Osuch T 2016 Appl. Opt. 55 4505
Google Scholar
[22] Silva S F O, Ferreira L A, Araújo F M, Santos J L, Frazão O 2011 Fiber Integr.Opt. 30 9
Google Scholar
[23] Zhuo Z C, Ham B S 2009 Opt. Fiber Technol. 15 442
Google Scholar
[24] 曹后俊, 司金海, 陈涛, 王瑞泽, 高博, 闫理贺, 侯洵 2018 中国激光 45 0702009
Cao H J, Si J H, Chen T, Wang R Z, Gao B, Yan L H, Hou X 2018 Chin. J. Lasers. 45 0702009
下载:
计量
- 文章访问数: 7356
- PDF下载量: 102
- 被引次数: 0
