-
利用第一性原理计算研究了氟化物钙钛矿NaFeF3的基态电子态和磁构型, 并模拟分析了衬底应力和阴离子置换对材料基本物性的影响. 计算结果表明, NaFeF3块材的G-AFM磁基态十分稳定, 不会受到衬底应力调控以及F位氧掺杂的影响. 当低浓度掺杂(~8.3%)时, 氧离子倾向于替换FeF2面内的F, 形成非对称的Fe-O-Fe链, 导致产生局域极化. 此外, 不对等的Fe—O键还会在氧离子两侧的Fe上形成电荷序, 进而产生非零净磁矩. 值得注意的是, 该局域极化和亚铁磁性均源于不等位氧掺杂, 因此有可能通过外电场调控实现极化翻转并同时改变净磁矩的方向实现电控磁. 更高浓度的氧掺杂会使得Fe的化合价整体升高, Fe离子上的局部电荷序和净磁矩随之消失. 该研究结果有望促进氟化物的理论和实验研究, 并为多铁性材料的设计研发提供新的材料.
On the basis of first-principles calculations, the systematic researches of the structural, electronic and magnetic properties of NaFeF3 are carried out in the present work. The influences of anion substitution and strain effect are taken into consideration in the reaearch. First, the basic properties of the NaFeF3 bulk are determined. The fully relaxed structure exhibits a distinct GdFeO3-type distortion and a relatively weak Jahn-Teller distortion. The band gap is estimated at 3 eV from our DFT calculations with Hubbard U correction. Moreover, the magnetic structure is of G-type antiferromagnetism (G-AFM). This intrinsic G-AFM magnetic state is robust, and cannot be easily destroyed by small perturbations, includinganion doping and epitaxial strain. Secondly, we study the oxygen doping effect on the properties of material with considering the fact that the radius of oxygen anion is very close to that of fluoride anion, and the oxygen substitution can be accommodated by the further oxidation of iron cation from divalent to trivalent state. According to our energy comparison calculations, when one of the twelve F sites in the NaFeF3 unit cell is taken up by an oxygen anion, whose corresponding doping concentration is approximately 8.3%, the O ion is more likely to occupy the in-plane site of the FeF6 octahedron. This low concentration doping may induce unequal Fe—O bonds, which lead to diverse valence states of surrounding Fe cations, and therefore result in local polarization and non-zero net magnetic moment. The local dipole and magnetic moment are inherently correlated with each other due to the common origin, i.e., the incoordinate Fe—O bonds. Therefore, the net magnetic moment together with the local polarization may be reversed simultaneously by an external electric field. However, when the doping concentration is further increased to 33%, the overall iron valence will rise to a higher state where the local charge order and the net moment disappear. In addition, the electronic properties of NaFeF3 also show obvious change due to the influence of biaxial strain. Specifically, the energy gap decreases monotonically as the in-plane stress gradually changes from compression to extension. However, the band structure does not change significantly. The top of the valence band and the bottom of the conduction band are both located at the Gamma point, thus making it a direct bandgap semiconductor material with an adjustable energy gap. These findings may promote further theoretical and experimental research on fluoride family and introduce a new candidate to the multiferroic field. -
Keywords:
- first-principles calculation /
- fluoride /
- perovskite /
- oxygen-doping
[1] Millis A J 1998 Nature 392 147
Google Scholar
[2] Ohtomo A, Hwang H Y 2004 Nature 427 423
Google Scholar
[3] Chen H, Kolpak A M, Isamail-Beigi S 2010 Adv. Mater. 22 2881
Google Scholar
[4] Garcia-Castro A C, Romero A H, Bousquest E 2016 Phys. Rev. Lett. 116 117202
Google Scholar
[5] Margadonna S, Karotsis G 2006 J. Am. Chem. Soc. 128 16436
Google Scholar
[6] Binggeli N, Altarelli M 2004 Phys. Rev. B 70 085117
Google Scholar
[7] Yamauchi K, Picozzi S 2010 Phys. Rev. Lett. 105 10720
[8] Karamyan A A 1973 Phys. Stat. Sol. A 16 419
Google Scholar
[9] Brown-Acquaye H A, Lane A P, Inorg J 1981 Nucl. Chem. 43 3143
[10] Ni S, Ma J, Lv X, Yang X, Zhang L 2014 Mater. Lett. 124 264
Google Scholar
[11] Hao L, Liu K, Cheng S, Wang Y, Xu Y, Qian H 2017 Mater. Lett. 196 145
Google Scholar
[12] Wang R T, Tai E G, Chen J Y, Xu G, LaPierre R, Goktas N I, Hu N 2019 Ceram. Inter. 45 64
Google Scholar
[13] Dhanapala B D, Munasinghe H N, Suescun L, Rabuffetti F A 2017 Inorg. Chem. 56 13311
Google Scholar
[14] Bernal F L, Yusenko K V, Sottmann J, Drathen C, Guignard J, Lovvik O M, Crichton W A, Margadonna S 2014 Inorg. Mater. 53 12205
[15] Kresse G, Hafner J 1993 Phys. Rev. B 47 558
Google Scholar
[16] Kresse G, Furthmuller J 1996 Phys. Rev. B 54 11169
Google Scholar
[17] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[18] Perdew J P, Ruzsinszky A, Csonka G I, Vydrov O A, Scuseria G E, Constantin L A, Zhou X, Burke K 2008 Phys. Rev. Lett. 100 136406
Google Scholar
[19] Monkhorst H J, Pack J D 1976 Phys. Rev. B 13 5188
Google Scholar
[20] Alaria J, Borisov P, Dyer M S, Manning T D, Lepadatu S, Cain M G, Mishina E D, Sherstyuk N E, Ilyin N A, Hadermann J, Lederman D, Claridge J B, Rosseinsky M J 2014 Chem. Sci. 5 1599
Google Scholar
[21] Garcia-Castro A C, Romero A H, Bousquet E 2014 Phys. Rev. B 90 064113
Google Scholar
[22] Friedman Z, Melamud M, Makovsky J, Shaked H 1970 Phys. Rev. B 2 179
Google Scholar
[23] Shane J R, Lyons D H, Kestigian M 1967 J. Appl. Phys. 38 1280
Google Scholar
[24] Zheng X X, Wang D, Tang L M, Chen K Q 2015 Mod. Phys. Lett. B 29 1550137
[25] 颜送灵, 唐黎明, 赵宇清 2016 65 077301
Google Scholar
Yan S L, Tang L M, Zhao Y Q 2016 Acta Phys. Sin. 65 077301
Google Scholar
[26] Li X X, Yang J L 2016 Natl. Sci. Rev. 3 365
Google Scholar
-
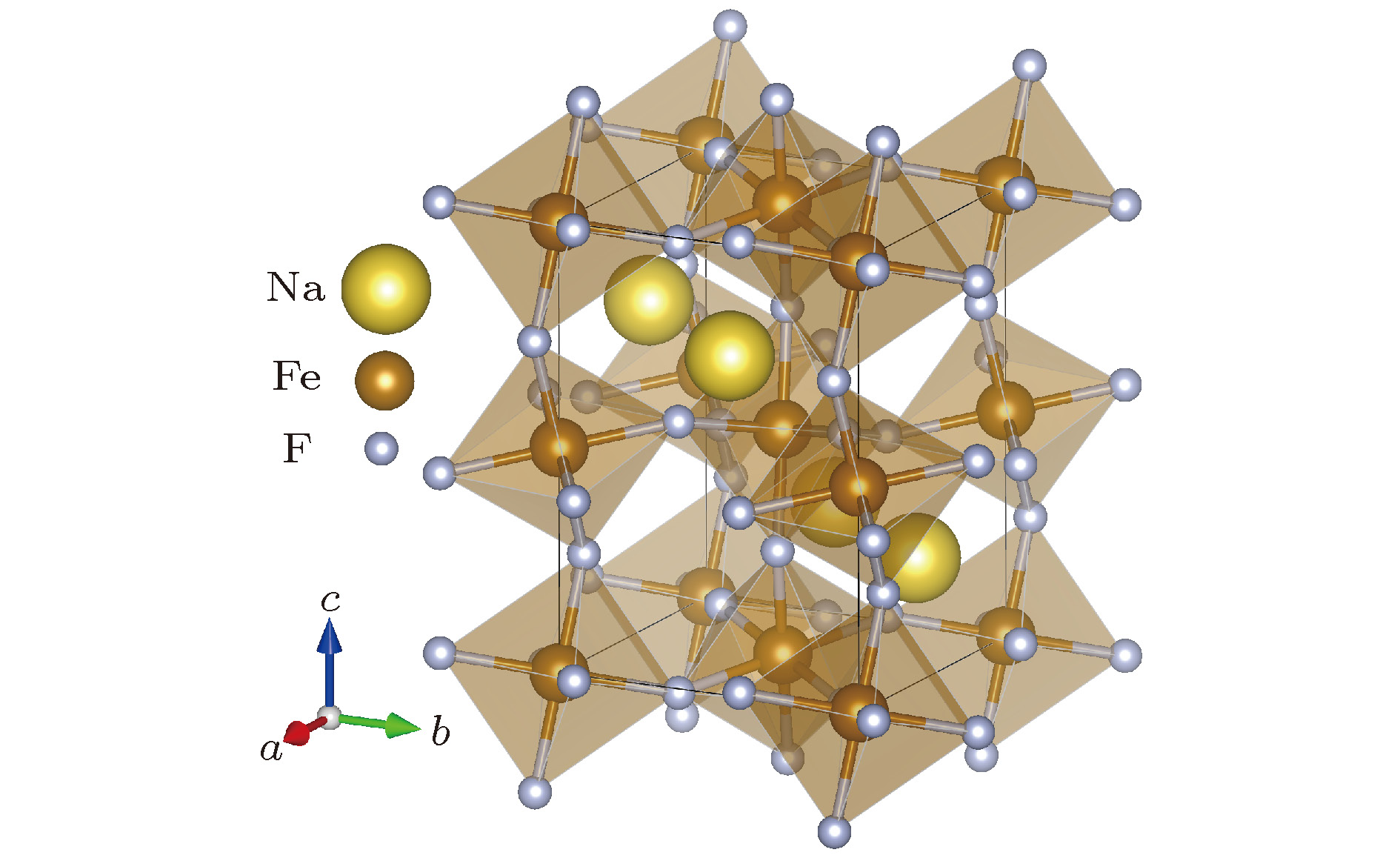
图 1 钙钛矿型氟化物NaFeF3的结构示意图 浅褐色的是由氟离子构成的FeF6八面体, 其中心为B位Fe离子, 近邻八面体之间通过共角F离子相连, A位Na离子位于FeF6八面体围成的三维框架中
Fig. 1. Schematic diagramof perovskite fluoride NaFeF3. The light brown structures are corner-sharing FeF6 octahedra. The center of octahedra are B-site iron ions, which are shown in dark brown. The yellow Na ions are located in the framework surrounded by the FeF6 octahedra
图 2 (a) NaFeF3块材的原子分波态密度图; (b) 块材中Fe2+离子的3d轨道分波态密度
Fig. 2. (a) The projected DOS of bulk NaFeF3; (b) the 3d orbital-projected DOS of Fe2+ ion.
图 3 面内双轴应力对NaFeF3块材中A-AFM, C-AFM, FM磁序以及G-AFM磁序之间相互能量差的影响, 以G-AFM能量作为参考值, 如虚线所示
Fig. 3. The biaxial strain dependent energy differences between A-AFM, C-AFM, G-AFM and FM states. The energy of G-AFM ground state is denoted by dash line for reference.
图 4 (a)−(e) 面内双轴应力作用下NaFeF3块材的态密度分布; (f) NaFeF3块材能带结构图; (g) NaFeF3块材带隙随应力的变化
Fig. 4. (a)–(e) The pDOS of NaFeF3 with different biaxial strain; (f) the representative band structure of NaFeF3 with –5% in-plane strain; (g) the biaxial strain dependent band gap diagram.
图 5 (a) 低浓度氧掺杂时, 费米面附近NaFeF3－xOx (x = 0.25)的原子分波态密度图; (b) 原胞中不同B位Fe离子的分波态密度, 其中插图为氧离子掺杂后的结构示意图, 为了清晰直观地表述, 图中仅给出Fe-F(O)八面体结构
Fig. 5. (a) The pDOS of NaFeF3－x Ox (x = 0.25) near Fermi level; (b) the PDOS of different B-site iron ions, which are specified in the inset, Na atoms are omitted for clarify.
图 6 高浓度氧掺杂后, NaFeF2O的总态密度和原子分波态密度图, 其中插图为相应的结构示意图
Fig. 6. The total DOS and pDOS of NaFeF2O near Fermi level; the structure is illustrated by the inset.
表 1 NaFeF3晶格优化后的结构参数与相应实验报道值
Table 1. Optimized structural parameters of NaFeF3 and the corresponding experimental values.
a/Å b/Å c/Å Space group Fe-F ∠Fe—F—Fe ab plane c axis ab plane c axis GGA + U 5.47 5.67 7.78 Pnma 2.096 2.029 2.052 145.5 143.0 Expt.[14] 5.48 5.66 7.88 Pnma 2.084 2.052 2.072 144.6 143.9 
下载: 导出CSV
-
[1] Millis A J 1998 Nature 392 147
Google Scholar
[2] Ohtomo A, Hwang H Y 2004 Nature 427 423
Google Scholar
[3] Chen H, Kolpak A M, Isamail-Beigi S 2010 Adv. Mater. 22 2881
Google Scholar
[4] Garcia-Castro A C, Romero A H, Bousquest E 2016 Phys. Rev. Lett. 116 117202
Google Scholar
[5] Margadonna S, Karotsis G 2006 J. Am. Chem. Soc. 128 16436
Google Scholar
[6] Binggeli N, Altarelli M 2004 Phys. Rev. B 70 085117
Google Scholar
[7] Yamauchi K, Picozzi S 2010 Phys. Rev. Lett. 105 10720
[8] Karamyan A A 1973 Phys. Stat. Sol. A 16 419
Google Scholar
[9] Brown-Acquaye H A, Lane A P, Inorg J 1981 Nucl. Chem. 43 3143
[10] Ni S, Ma J, Lv X, Yang X, Zhang L 2014 Mater. Lett. 124 264
Google Scholar
[11] Hao L, Liu K, Cheng S, Wang Y, Xu Y, Qian H 2017 Mater. Lett. 196 145
Google Scholar
[12] Wang R T, Tai E G, Chen J Y, Xu G, LaPierre R, Goktas N I, Hu N 2019 Ceram. Inter. 45 64
Google Scholar
[13] Dhanapala B D, Munasinghe H N, Suescun L, Rabuffetti F A 2017 Inorg. Chem. 56 13311
Google Scholar
[14] Bernal F L, Yusenko K V, Sottmann J, Drathen C, Guignard J, Lovvik O M, Crichton W A, Margadonna S 2014 Inorg. Mater. 53 12205
[15] Kresse G, Hafner J 1993 Phys. Rev. B 47 558
Google Scholar
[16] Kresse G, Furthmuller J 1996 Phys. Rev. B 54 11169
Google Scholar
[17] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[18] Perdew J P, Ruzsinszky A, Csonka G I, Vydrov O A, Scuseria G E, Constantin L A, Zhou X, Burke K 2008 Phys. Rev. Lett. 100 136406
Google Scholar
[19] Monkhorst H J, Pack J D 1976 Phys. Rev. B 13 5188
Google Scholar
[20] Alaria J, Borisov P, Dyer M S, Manning T D, Lepadatu S, Cain M G, Mishina E D, Sherstyuk N E, Ilyin N A, Hadermann J, Lederman D, Claridge J B, Rosseinsky M J 2014 Chem. Sci. 5 1599
Google Scholar
[21] Garcia-Castro A C, Romero A H, Bousquet E 2014 Phys. Rev. B 90 064113
Google Scholar
[22] Friedman Z, Melamud M, Makovsky J, Shaked H 1970 Phys. Rev. B 2 179
Google Scholar
[23] Shane J R, Lyons D H, Kestigian M 1967 J. Appl. Phys. 38 1280
Google Scholar
[24] Zheng X X, Wang D, Tang L M, Chen K Q 2015 Mod. Phys. Lett. B 29 1550137
[25] 颜送灵, 唐黎明, 赵宇清 2016 65 077301
Google Scholar
Yan S L, Tang L M, Zhao Y Q 2016 Acta Phys. Sin. 65 077301
Google Scholar
[26] Li X X, Yang J L 2016 Natl. Sci. Rev. 3 365
Google Scholar
下载:
计量
- 文章访问数: 11130
- PDF下载量: 149
- 被引次数: 0
