-
基于成熟的光纤激光器、光纤放大器及高效激光频率转换技术, 我们在实验中研制了一套瓦级输出的窄线宽连续波单频可调谐318.6 nm紫外激光系统, 并在室温铯原子气室中实现了6S1/2—nP3/2 (n = 70—94)单光子跃迁里德伯激发. 借助由铯原子6S1/2 (F = 4)基态、6P3/2 (F ′= 5)激发态和nP3/2 (n = 70—94)里德伯态构成的V型三能级系统, 通过频率锁定于铯原子6S1/2 (F = 4)—6P3/2 (F ′ = 5)超精细跃迁的852.3 nm探测光束的吸收减弱信号获得了里德伯态的信息, 并利用高精度波长计测量了铯原子nP3/2 (n = 70—94)里德伯态的量子亏损值. 经过与理论计算值的变化趋势进行对比, 我们认为由于原子气室的里德伯屏蔽效应并不能完全屏蔽外部直流电场, 铯原子气室内存在残余的直流电场, 影响了对里德伯态的量子亏损值的实验测量. 利用残余直流电场的Stark效应理论模型及其与有效主量子数n*的依赖关系, 对铯原子里德伯态的量子亏损实验测量值进行了修正. 修正后的铯原子nP3/2 (n = 70—94)态量子亏损测量值为3.5591 ± 0.0007, 与理论计算值相吻合.A narrow-linewidth continuous-wave single-frequency tunable 318.6-nm ultraviolet laser system with watt-level output power is developed in our experiment based on well-developed fiber lasers, fiber amplifiers, and efficient laser frequency conversion technique. Cesium 6S1/2—nP3/2 (n = 70—94) single-photon Rydberg excitation in a room-temperature cesium atomic vapor cell is realized by using our ultraviolet laser system. The single-photon Rydberg excitation signal is obtained via the V-type three-level atomic system which contains 6S1/2 (F = 4) ground state, 6P3/2 (F = 5) excited state and one of nP3/2 (n = 70—94) Rydberg states. When cesium atoms populated on the ground state are partially excited to Rydberg state by the ultraviolet laser, absorption of 852.3-nm probe beam which is locked to 6S1/2 (F = 4)—6P3/2 (F ′ = 5) hyperfine transition will decrease. In this way, the cesium Rydberg states are detected. The quantum defects for cesium nP3/2 (n = 70—94) Rydberg states are experimentally measured with a high-precision wavemeter. The variation trend of experimentally measured data deviates from that of calculated values. Due to the fact that the cesium vapor cell is positioned in a magnetic shielding tank, the Zeeman effect can be ignored. Considering that the polarizability of Rydberg atoms is proportional to (n*)7, in which n* is the effective principal quantum number, the Rydberg screen effect of cesium atomic vapor cell cannot completely protect cesium atoms from being perturbed by an external DC electric field. Therefore the residual DC electric field existing inside the cesium vapor cell will have a significant influence on quantum defect measurement of Rydberg atoms. Using the theoretical model of Stark effect and the relationship between polarizability of Rydberg atoms and the effective principal quantum number n*, the corrected experimental value of quantum defect for cesium nP3/2 (n = 70—94) Rydberg states is found to be ~(3.5591 ± 0.0007). The corrected experimental value of quantum defect is consistent with the calculation.
[1] Gallagher T F1994 Rydberg Atoms (Cambridge: Cambridge University Press) p12
[2] Zimmerman M L, Littman M G, Kash M M, Kleppner D 1979 Phys. Rev. A 20 2251
Google Scholar
[3] Sedlacek J A, Schwettmann A, Kübler H, Shaffer J P 2013 Phys. Rev. Lett. 111 063001
Google Scholar
[4] Carter J D, Cherry O, Martin J D D 2012 Phys. Rev. A 86 053401
Google Scholar
[5] Sedlacek J A, Schwettmann A, Kübler H, Löw R, Pfau T, Shaffer J P 2012 Nature Phys. 8 819
Google Scholar
[6] Zhao B, Müller M, Hammerer K, Zoller P 2010 Phys. Rev. A 81 052329
Google Scholar
[7] Wilk T, Gaëtan A, Evellin C, Wolters J, Miroshnychenko Y, Grangier P, Browaeys A 2010 Phys. Rev. Lett. 104 010502
Google Scholar
[8] Isenhower L, Urban E, Zhang X L, Gill A T, Henage T, Johnson T A, Walker T G, Saffman M 2010 Phys. Rev. Lett. 104 010503
Google Scholar
[9] Saffman M, Walker T G, Mølmer K 2010 Rev. Mod. Phys. 82 2313
Google Scholar
[10] Urban E, Johnson T A, Henage T, Isenhower L, Yavuz D D, Walker T G, Saffman M 2009 Nature Phys. 5 110
Google Scholar
[11] Gaëtan A, Miroshnychenko Y, Wilk T, Chotia A, Viteau M, Comparat D, Pillet P, Browaeys A, Grangier P 2009 Nature Phys. 5 115
Google Scholar
[12] Hankin A M, JauY Y, Parazzoli L P, Chou C W, Armstrong D J, Landahl A J, Biedermann G W 2014 Phys. Rev. A 89 033416
Google Scholar
[13] Dudin Y O, Kuzmich A 2012 Science 336 887
Google Scholar
[14] Keating T, Goyal K, Jau Y Y, Biedermann G W, Landahl A J, Deutsch I H 2013 Phys. Rev. A 87 052314
Google Scholar
[15] Wang J Y, Bai J D, He J, Wang J M 2016 J. Opt. Soc. Am. B 33 2020
[16] Lorenzen C J, Niemax K 1984 Z. Phys. A: Atoms and Nuclei 315 127
Google Scholar
[17] Li W H, Mourachko I, Noel M W, Gallagher T F 2003 Phys. Rev. A 67 052502
Google Scholar
[18] Wang J Y, Bai J D, He J, Wang J M 2017 Opt. Express 25 22510
Google Scholar
[19] Baugh J F, Ciocca M, Edmonds D A, Nellesen P T, Burkhardt C E, Leventhal J J 1996 Phys. Rev. A 54 R4641
Google Scholar
[20] Gallagher T F, Humphrey L M, Hill R W, Cooke W E, Edelstein S A 1977 Phys. Rev. A 15 1937
Google Scholar
[21] 杨智伟, 焦月春, 韩小萱, 赵建明, 贾锁堂 2017 66 093202
Google Scholar
Yang Z W, Jiao Y C, Han X X, Zhao J M, Jia S T 2017 Acta Phys. Sin. 66 093202
Google Scholar
[22] Osterwalder A, Merkt F 1999 Phys. Rev. Lett. 82 1831
Google Scholar
[23] 李昌勇, 张临杰, 赵建明, 贾锁堂 2012 61 163202
Google Scholar
Li C Y, Zhang L J, Zhao J M, Jia S T 2012 Acta Phys. Sin. 61 163202
Google Scholar
[24] 何兴虹, 李白文, 张承修 1989 38 1717
Google Scholar
He X H, Li B W, Zhang C X 1989 Acta Phys. Sin. 38 1717
Google Scholar
[25] Bai J D, Wang J Y, Liu S, He J, Wang J M 2018 arXiv:1811.05092v1 [physics.atom-ph]
-
图 1 (a) 铯原子V型三能级系统, 318.6 nm紫外光将原子从6S1/2 (F = 4)基态激发到nP3/2 (n = 70—94)里德伯态,
${\varDelta_c}$ 为激发光相对跃迁频率的失谐量; 852.3 nm探测光频率锁定在6S1/2 (F = 4)—6P3/2 (F' = 5)超精细跃迁; (b)实验装置示意图; OI, 光隔离器; EOM, 带输入和输出尾纤的集成光波导型电光位相调制器; PBS, 偏振分束棱镜; BS, 分束片; DM, 双色片; DPD, 差分探测器;$\Omega $ , EOM所加的射频调制信号Fig. 1. (a) The V-type cesium three-level system; a 318.6 nm ultraviolet laser excited partial cesium atoms from 6S1/2 (F = 4) ground state to nP3/2 (n = 70–94) Rydberg state, where
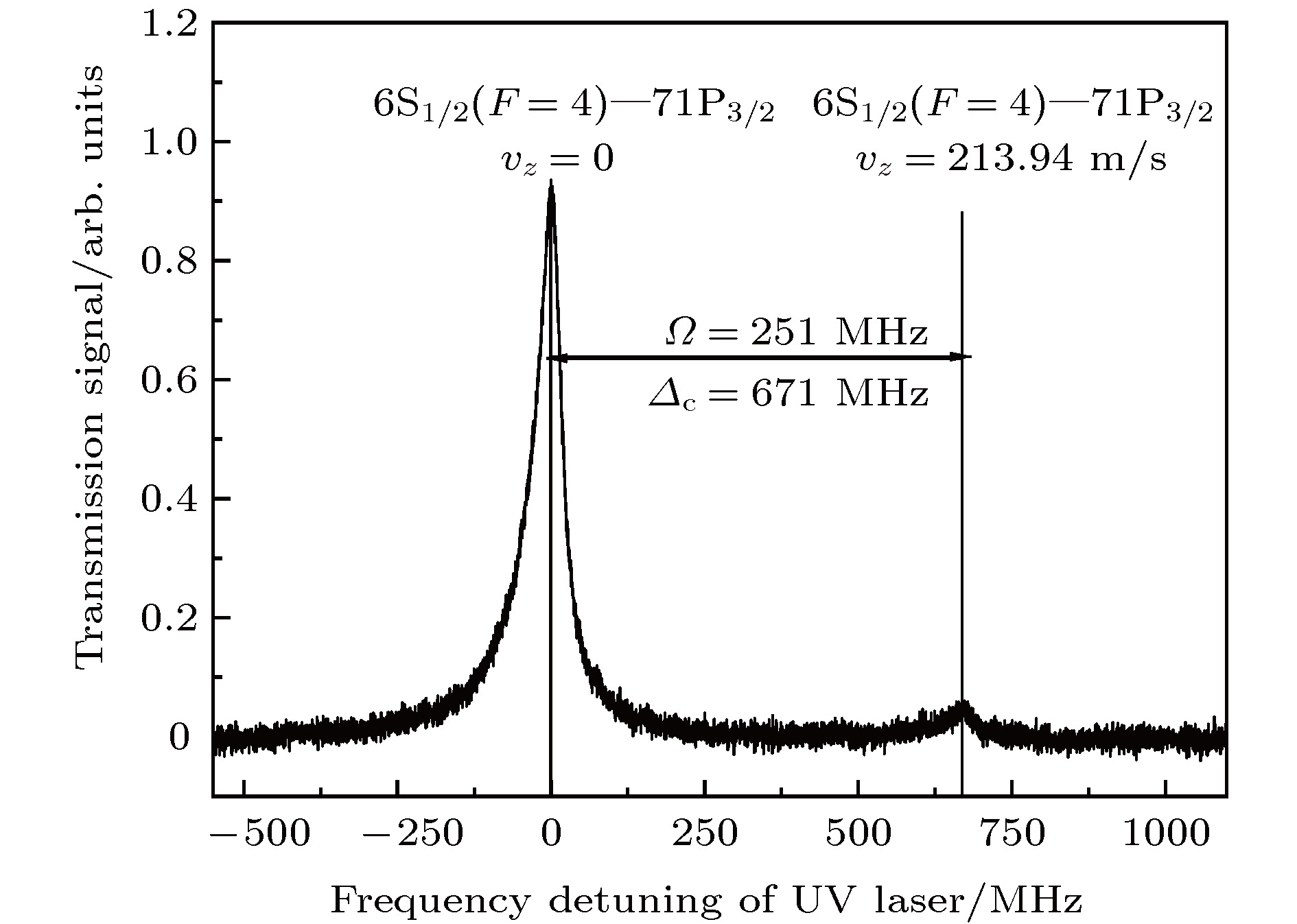
${\varDelta_c}$ is the frequency detuning of pump laser; a 852.3 nm probe laser is locked to 6S1/2 (F = 4) –6P3/2 (F' = 5) hyperfine transition. (b) Schematic diagram of experimental setup. OI, optical isolator; EOM, fiber-pigtailed integration optical waveguide phase-type electro-optic modulator; PBS, polarization beam spliter cube; BS, beam spliter plate; DM, dichroic mirror; DPD, differential photo-diode; Ω, the radio-frequency modulated signal applied on EOM
图 2 速度选择单光子跃迁铯原子71P3/2里德伯态的激发光谱. 852.3 nm探测光共振于6S1/2 (F = 4)—6P3/2 (F' = 5)跃迁线, 探测光功率为159
$\;{\text{μW}}$ ; 318.6 nm紫外激发光频率在6S1/2 (F = 4)—71P3/2态跃迁扫描, 功率为1.6 W; 激发光频率相对71P3/2态零失谐和蓝失谐671 MHz时, 出现两个透射信号, 分别对应速度组分为vz=0 (对应852.3 nm探测光的载频)和vz=213.94 m/s (对应852.3 nm探测光的 + 1级251 MHz射频调制边带)的铯原子被激发到71P3/2态Fig. 2. Velocity-selective spectra. The frequency of 852.3 nm probe beam is locked on the 6S1/2 (F = 4)—6P3/2 (F' = 5) transition and the light power is 159
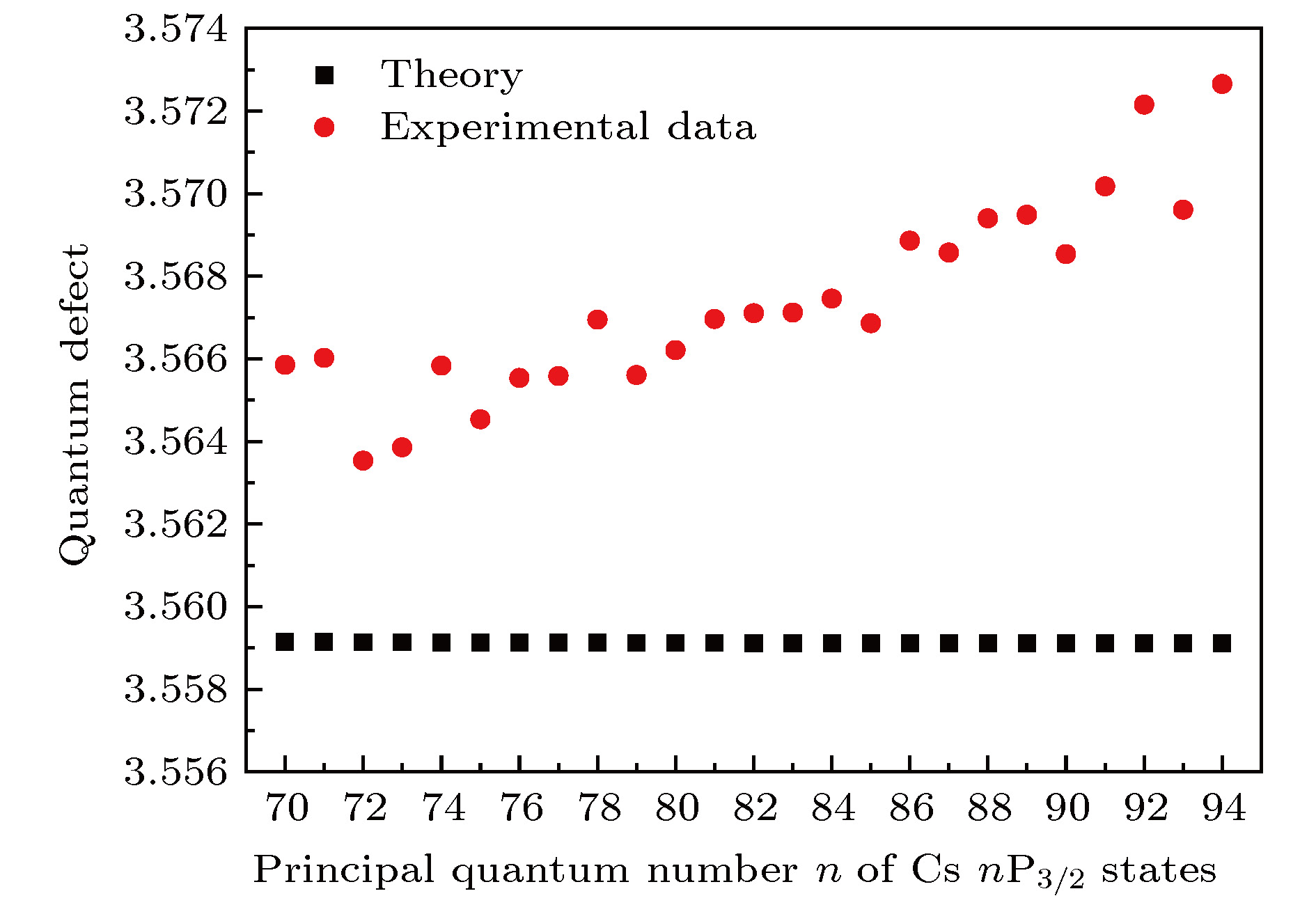
$\;{\text{μW}}$ ; the 318.6 nm coupling beam is scanned over the transition of 6S1/2 (F = 4)—71P3/2 and the light power is 1.6 W. Two transmission peaks appeared when the frequency of the coupling beam resonated with the 6S1/2 (F = 4)—71P3/2 transition line or blue detuning of 671 MHz, corresponding to atoms which have velocity of vz = 0 (corresponding to the carrier of 852.3 nm probe beam) and vz = 213.94 m/s (corresponding to the +1 order 251 MHz radio-frequency modulation component of 852.3 nm probe beam) are excited to 71P3/2 Rydberg state, respectively.
图 3 铯原子nP3/2 (n = 50—100)里德伯态量子亏损随主量子数n的变化. 量子亏损随着主量子数n增加而缓慢减小
Fig. 3. The theory values of quantum defects for cesium nP3/2 (n = 50–100) Rydberg states. Quantum defect is decreasing with increasing of the principal quantum number n.
图 4 铯原子nP3/2 (n = 70—94)态的量子亏损计算值与实验直接测量值的对比. 其中红色圆点为计算值, 黑色方块为实验直接测量值; 随着主量子数n的增加, 计算值近乎不变, 而实验直接测量值却是增加的. 这一趋势表明有一些影响因素必须要考虑, 去修正直接实验测量得到的铯原子nP3/2 (n = 70—94)里德伯态的量子亏损值
Fig. 4. Comparison of direct experimentally measured data with calculated values of quantum defects for cesium nP3/2 (n = 70—94) Rydberg states. The red dots are calculated values and the black cubes are direct experimentally measured data. When the principal quantum number n increasing, the calculated values are almost constant, but the direct experimentally measured data are increasing obviously. This variation trend indicate that some influence factors should be took into account to correct the direct experimentally measured data.
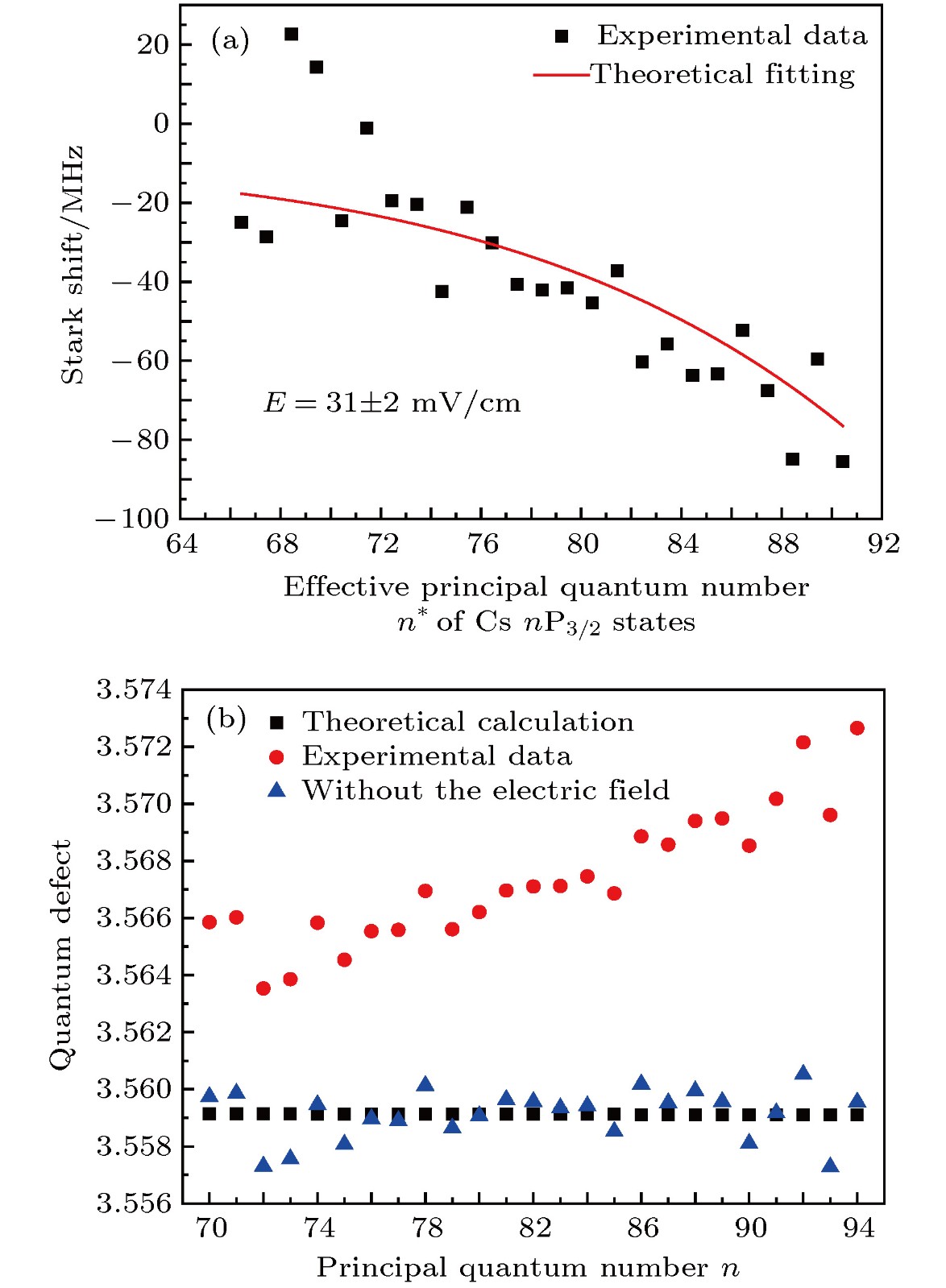
图 5 (a) 利用估算的残余直流电场对量子亏损直接实验测量值进行修正, 根据Stark频移量和有效主量子数n*的关系, 拟合得到了作用于铯原子气室中的残余直流电场约为 (31 ± 2) mV/cm; (b) 修正Stark效应及波长计测量误差的影响后, 铯原子nP3/2(n = 70—94)态量子亏损的实验测量修正值约3.5591 ± 0.0007; 实验数据与计算值相吻合
Fig. 5. (a) Using the estimated residual DC electric field to correct the direct experimentally measured data, according to the relationship between Stark shift and effective principal quantum number n*, the magnitude of the residual DC electric field acting on the cesium atomic vapor cell is ~(31 ± 2) mV/cm; (b) after correction of the impact of Stark effect and the measurement error of wavemeter, the corrected experimentally measured quantum defect value of cesium nP3/2 (n = 70—94) states is ~(3.5591 ±0.0007). This corrected result is consistent with the theoretically calculated value.
表 1 铯原子高激发nP3/2 (n = 70—94)里德伯态的极化率
Table 1. Polarizability of highly-excited Cs nP3/2 (n = 70—94) Rydberg states.
Principal quantum number Polarizability/MHz/(V/cm)2 Principal quantum number Polarizability/MHz/(V/cm)2 70 15730.1 83 54913.3 71 17463.0 84 59935.9 72 19356.9 85 65347.2 73 21424.3 86 71172.0 74 23678.2 87 77436.3 75 26132.3 88 84167.3 76 28801.2 89 91393.7 77 31700.5 90 99145.6 78 34846.4 91 107454.3 79 38256.2 92 116352.9 80 41948.1 93 125875.7 81 45941.3 94 136058.9 82 50255.9 - - 
下载: 导出CSV
-
[1] Gallagher T F1994 Rydberg Atoms (Cambridge: Cambridge University Press) p12
[2] Zimmerman M L, Littman M G, Kash M M, Kleppner D 1979 Phys. Rev. A 20 2251
Google Scholar
[3] Sedlacek J A, Schwettmann A, Kübler H, Shaffer J P 2013 Phys. Rev. Lett. 111 063001
Google Scholar
[4] Carter J D, Cherry O, Martin J D D 2012 Phys. Rev. A 86 053401
Google Scholar
[5] Sedlacek J A, Schwettmann A, Kübler H, Löw R, Pfau T, Shaffer J P 2012 Nature Phys. 8 819
Google Scholar
[6] Zhao B, Müller M, Hammerer K, Zoller P 2010 Phys. Rev. A 81 052329
Google Scholar
[7] Wilk T, Gaëtan A, Evellin C, Wolters J, Miroshnychenko Y, Grangier P, Browaeys A 2010 Phys. Rev. Lett. 104 010502
Google Scholar
[8] Isenhower L, Urban E, Zhang X L, Gill A T, Henage T, Johnson T A, Walker T G, Saffman M 2010 Phys. Rev. Lett. 104 010503
Google Scholar
[9] Saffman M, Walker T G, Mølmer K 2010 Rev. Mod. Phys. 82 2313
Google Scholar
[10] Urban E, Johnson T A, Henage T, Isenhower L, Yavuz D D, Walker T G, Saffman M 2009 Nature Phys. 5 110
Google Scholar
[11] Gaëtan A, Miroshnychenko Y, Wilk T, Chotia A, Viteau M, Comparat D, Pillet P, Browaeys A, Grangier P 2009 Nature Phys. 5 115
Google Scholar
[12] Hankin A M, JauY Y, Parazzoli L P, Chou C W, Armstrong D J, Landahl A J, Biedermann G W 2014 Phys. Rev. A 89 033416
Google Scholar
[13] Dudin Y O, Kuzmich A 2012 Science 336 887
Google Scholar
[14] Keating T, Goyal K, Jau Y Y, Biedermann G W, Landahl A J, Deutsch I H 2013 Phys. Rev. A 87 052314
Google Scholar
[15] Wang J Y, Bai J D, He J, Wang J M 2016 J. Opt. Soc. Am. B 33 2020
[16] Lorenzen C J, Niemax K 1984 Z. Phys. A: Atoms and Nuclei 315 127
Google Scholar
[17] Li W H, Mourachko I, Noel M W, Gallagher T F 2003 Phys. Rev. A 67 052502
Google Scholar
[18] Wang J Y, Bai J D, He J, Wang J M 2017 Opt. Express 25 22510
Google Scholar
[19] Baugh J F, Ciocca M, Edmonds D A, Nellesen P T, Burkhardt C E, Leventhal J J 1996 Phys. Rev. A 54 R4641
Google Scholar
[20] Gallagher T F, Humphrey L M, Hill R W, Cooke W E, Edelstein S A 1977 Phys. Rev. A 15 1937
Google Scholar
[21] 杨智伟, 焦月春, 韩小萱, 赵建明, 贾锁堂 2017 66 093202
Google Scholar
Yang Z W, Jiao Y C, Han X X, Zhao J M, Jia S T 2017 Acta Phys. Sin. 66 093202
Google Scholar
[22] Osterwalder A, Merkt F 1999 Phys. Rev. Lett. 82 1831
Google Scholar
[23] 李昌勇, 张临杰, 赵建明, 贾锁堂 2012 61 163202
Google Scholar
Li C Y, Zhang L J, Zhao J M, Jia S T 2012 Acta Phys. Sin. 61 163202
Google Scholar
[24] 何兴虹, 李白文, 张承修 1989 38 1717
Google Scholar
He X H, Li B W, Zhang C X 1989 Acta Phys. Sin. 38 1717
Google Scholar
[25] Bai J D, Wang J Y, Liu S, He J, Wang J M 2018 arXiv:1811.05092v1 [physics.atom-ph]
下载:
计量
- 文章访问数: 8715
- PDF下载量: 109
- 被引次数: 0
