-
基于五步激光共振激发, 经由中间态(Xe)
$ 5{\rm d}6{\rm d} \; ^3{\rm F}_2 $ 的一价镧离子光谱, 分析了该实验谱, 确定了一价镧离子一强一弱两个自电离里德伯系列. 同时利用多通道量子亏损理论(MQDT)框架下的相对论多通道理论(RMCT)计算, 标识了这两个自电离里德伯系列, 强的自电离里德伯系列标识为$ 5{dnp}\left(\dfrac{5}{2},\dfrac{1}{2}\right)_3 $ 和/或$ 5{ dnp}\left(\dfrac{5}{2},\dfrac{1}{2}\right)_2 $ , 弱系列标识为为$ 5{ dnf}\left(\dfrac{5}{2},\dfrac{5}{2}\right)_3 $ 和/或$ 5{dnf}\left(\dfrac{5}{2},\dfrac{5}{2}\right)_2 $ . 根据实验谱峰数据, 发现有效量子数很高时, 里德伯和自电离里德伯能级量子数亏损随激发能量不平滑变化, 并分析了可能的原因.We analyze ionic spectrum of lanthanum via intermediate state (Xe)$ 5d6d \; ^3F_2 $ in the energy region 89872-91783 cm–1, and the spectrum is obtained using five-laser resonance excitation in combination with a method of sequential ionization by a pulsed electric field and a constant electric field, and has been recalibrate in this work. Both of one strong and one weak autoionization Rydberg series converging to the La2+ state are determined. Meanwhile, the two autoionization Rydberg series are assigned by relativistic multichannel theory (RMCT) within the framework of multi-channel quantum defect theory (MQDT). More specifically, the strong autoionization Rydberg series is assigned to$ 5dnp\left(\dfrac{5}{2},\dfrac{1}{2}\right)_3 $ and/or$ 5dnp\left(\dfrac{5}{2},\dfrac{1}{2}\right)_2 $ , and the weak autoionization Rydberg series is assigned to$ 5dnf\left(\dfrac{5}{2},\dfrac{5}{2}\right)_3 $ and/or$ 5dnf\left(\dfrac{5}{2},\dfrac{5}{2}\right)_2 $ . We focus on the behavior of quantum defect with excitation energy for high$ n $ Rydberg states, which are sensitive to the existence of a external field. We find the breakdown of quantum defect regular behavior for a specific Rydberg series and autoionization Rydberg series of La+ as the effective quantum number$ n^\star>67 $ . Due to that our calculations, which are obtained by relativistic multichannel theory and included configuration interactions, are in basically agreement with that for experimental low$ n $ ($ n^\star<67 $ ) Rydberg states as well as small stray electric fields, we suggest that plasma formed by photoionization of La atoms in the second excitation step may be responsible for the breakdown of quantum defect regular behavior.-
Keywords:
- quantum defect /
- Rydberg state /
- relativistic multi-channel theory
[1] Xie X P, Xu C B, Sun W, Xue P, Zhong Z P, Huang W, Xu X Y 1999 J. Opt. Soc. Am. B 16 484
 Google Scholar
Google Scholar
[2] Kramida A, Ralchenko Y, Reader J, Team, NIST A S D url: https://physics.nist.gov/asd [2018-12-1]
[3] Fano U 1970 Phys. Rev. A 2 353
 Google Scholar
Google Scholar
[4] Lee C M, Lu K T 1973 Phys. Rev. A 8 1241
 Google Scholar
Google Scholar
[5] Greene C, Fano U, Strinati G 1979 Phys. Rev. A 19 1485
 Google Scholar
Google Scholar
[6] Johnson W R, Lin C D, Cheng K T, Lee C M 1980 Phys. Scr. 21 409
 Google Scholar
Google Scholar
[7] 李家明 1980 29 419
 Google Scholar
Google Scholar
Li J M 1980 Acta Phys. Sin. 29 419
 Google Scholar
Google Scholar
[8] Seaton M J 1983 Rep. Prog. Phys. 46 167
 Google Scholar
Google Scholar
[9] 李家明 1983 32 84
 Google Scholar
Google Scholar
Li J M 1983 Acta Phys. Sin. 32 84
 Google Scholar
Google Scholar
[10] Lee C M 1974 Phys. Rev. A 10 584
 Google Scholar
Google Scholar
[11] 邹宇, 仝晓民, 李家明 1995 44 50
 Google Scholar
Google Scholar
Zou Y, Tong X M, Li J M 1995 Acta Phys. Sin. 44 50
 Google Scholar
Google Scholar
[12] Huang W, Zou Y, Tong X M, Li J M 1995 Phys. Rev. A 52 2770
 Google Scholar
Google Scholar
[13] 颜君, 张培鸿, 仝晓民, 李家明 1996 45 1978
 Google Scholar
Google Scholar
Yan J, Zhang P H, Tong X M, Li J M 1996 Acta Phys. Sin. 45 1978
 Google Scholar
Google Scholar
[14] Li J M, Wu Y J, Pratt R H 1989 Phys. Rev. A 40 3036
 Google Scholar
Google Scholar
[15] Xia D, Li J M 2001 Chin. Phys. Lett. 18 1334
 Google Scholar
Google Scholar
[16] Xia D, Zhang S Z, Peng Y L, Li J M 2003 Chin. Phys. Lett. 20 56
 Google Scholar
Google Scholar
[17] Sun W, Yan J, Zhong Z P, Xie X P, Xue P, Xu X Y 2001 J. Phys. B: At. Mol. Opt. Phys. 34 369
 Google Scholar
Google Scholar
[18] Zhang X F, Jia F D, Zhong Z P, Xue P, Xu X Y, Yan J 2007 Chin. Phys. Lett. 24 2808
 Google Scholar
Google Scholar
[19] Wang J Y, Zhong Z P, Jia F D, Qu Y Z, Zhong Y P 2008 J. Phys. B: At. Mol. Opt. Phys. 41 085002
 Google Scholar
Google Scholar
[20] Zhong Y P, Jia F D, Zhong Z P 2009 Chin. Phys. B 18 4242
 Google Scholar
Google Scholar
[21] Sedlacek J A, Schwettmann A, Kübler H, Löw R, Pfau T, Shaffer J P 2012 Nat. Phys. 8 819
 Google Scholar
Google Scholar
[22] 黄巍, 梁振涛, 杜炎雄, 颜辉, 朱诗亮 2015 64 160702
 Google Scholar
Google Scholar
Huang W, Liang Z T, Du Y X, Yan H, Zhu S L 2015 Acta Phys. Sin. 64 160702
 Google Scholar
Google Scholar
[23] 孙玮 2001 博士学位论文 (北京: 清华大学)
Sun W 2001 Ph. D. Dissertation (Beijing: Tsinghua University) (in Chinese)
[24] Huang W, Xu X Y, Xu C B, Xue M, Chen D Y 1995 J. Opt. Soc. Am. B 12 961
 Google Scholar
Google Scholar
[25] Huang W, Xu X Y, Xu C B, Xue M, Li L Q, Chen D Y 1994 Phy. Rev. A 49 R653
 Google Scholar
Google Scholar
[26] 赵中新, 李家明 1985 34 1469
 Google Scholar
Google Scholar
Zhao Z X, Li J M 1985 Acta Phys. Sin. 34 1469
 Google Scholar
Google Scholar
[27] 李心梅, 阮亚平, 钟志萍 2012 61 023104
 Google Scholar
Google Scholar
Li X M, Ruan Y P, Zhong Z P 2012 Acta Phys. Sin. 61 023104
 Google Scholar
Google Scholar
[28] Jia F D, Zhong Z P, Sun W, Xue P, Xu X Y 2009 Phys. Rev. A 79 032505
 Google Scholar
Google Scholar
[29] Lv S F, Li R, Jia F D, Li X K, Lassen J, Zhong Z P 2017 Chin. Phys. Lett. 34 073101
 Google Scholar
Google Scholar
[30] Li R, Lassen J, Zhong Z P, Jia F D, Mostamand M, Li X K, Reich B B, Teigelhöfer A, Yan H 2017 Phy. Rev. A 95 052501
 Google Scholar
Google Scholar
[31] Gallagher T F 1994 Rydberg Atom (1st Ed.) (Cambridge: Cambridge University Press) pp 70–102
[32] Ecker G, Kröll W 1963 Phys. Fluids 6 62
 Google Scholar
Google Scholar
[33] Stewart J C, Pyatt Jr. K D 1966 Astrophys. J. 144 1203
 Google Scholar
Google Scholar
[34] Qi Y Y, Wang J G, Janev R K 2008 Phys. Rev. A 78 062511
 Google Scholar
Google Scholar
[35] Lyon M, Rolston S L 2017 Rep. Prog. Phys. 80 017001
 Google Scholar
Google Scholar
[36] Park H, Ali R, Gallagher T F 2010 Phys. Rev. A 82 023421
 Google Scholar
Google Scholar
-
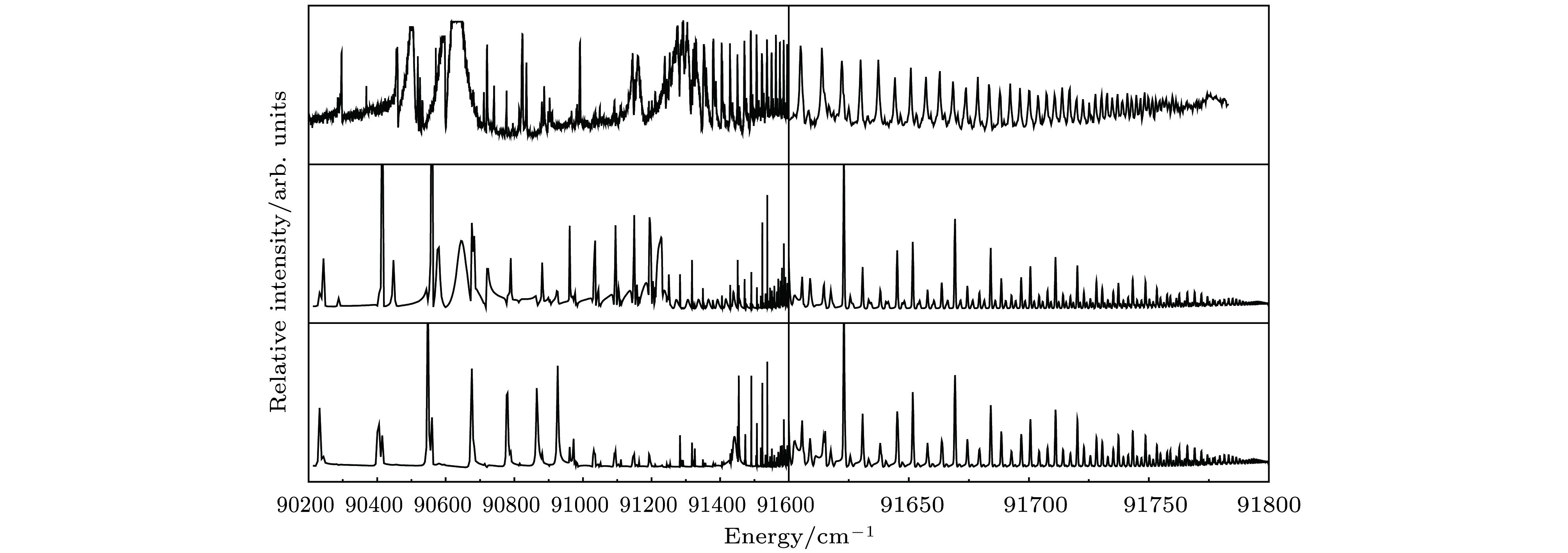
图 1 由中间态(Xe)
$ 5{\rm d}6{\rm d} \; ^3{\rm F}_2 $ 激发的一价镧离子光谱的能量标定: 以文献[1]的89690.4—91639.8 cm–1光谱(下图)为基准, 对89872.8—91783.2 cm–1能区光谱(上图)[19]重新标定, 平移了–10.3 cm–1. 横轴能量以一价镧离子基态能量为零点Fig. 1. The energy calibration of the excited La+ spectrum via intermediate state (Xe)
$ 5{\rm d}6{\rm d} \; ^3{\rm F}_2 $ . We recalibrate the spectrum[19] in the energy region 89872.8—91783.2 cm–1 (upper figure) according to the spectrum[1] in the energy region 89690.4—91639.8 cm–1(lower figure), and the offset of the recalibration is –10.3 cm–1. The zero point of energy is taken the energy of the ground state of La+.图 2 考虑了对实验谱有主要贡献的本征通道之间相互作用的理论光谱(中间谱)与实验谱(上图)和本征通道谱(下图)
$ 5{\rm d}\epsilon {\rm p}\left(\dfrac{5}{2}, \dfrac{1}{2}\right)_3, J^\pi=3^- $ 的比较. 中间的理论谱是根据(1)式, 考虑了$ J^\pi=3^- $ 的这些本征通道的相互作用:$ 5{\rm d}_{3/2}\epsilon {\rm f}_{5/2}$ ,$5d_{5/2}\epsilon f_{5/2}$ ,$5{\rm d}_{5/2}\epsilon {\rm p}_{1/2}$ ,$4{\rm f}_{5/2}\epsilon {\rm s}_{1/2}$ ,$4{\rm f}_{5/2}\epsilon {\rm d}_{3/2}$ ,$4{\rm f}_{7/2}\epsilon {\rm s}_{1/2}$ ,$4{\rm f}_{7/2}\epsilon {\rm d}_{3/2}$ ,$4{\rm f}_{7/2}\epsilon {\rm d}_{5/2} $ 和$ 6{\rm p}_{3/2}\epsilon {\rm d}_{5/2} $ Fig. 2. Comparison of the experimental spectrum(upper figure), the theoretical spectrum(middle figure) considering interaction among these eigenchannels that give primary contribution to the experimental spectra and the eigenchannel spetrum(lower figure) for
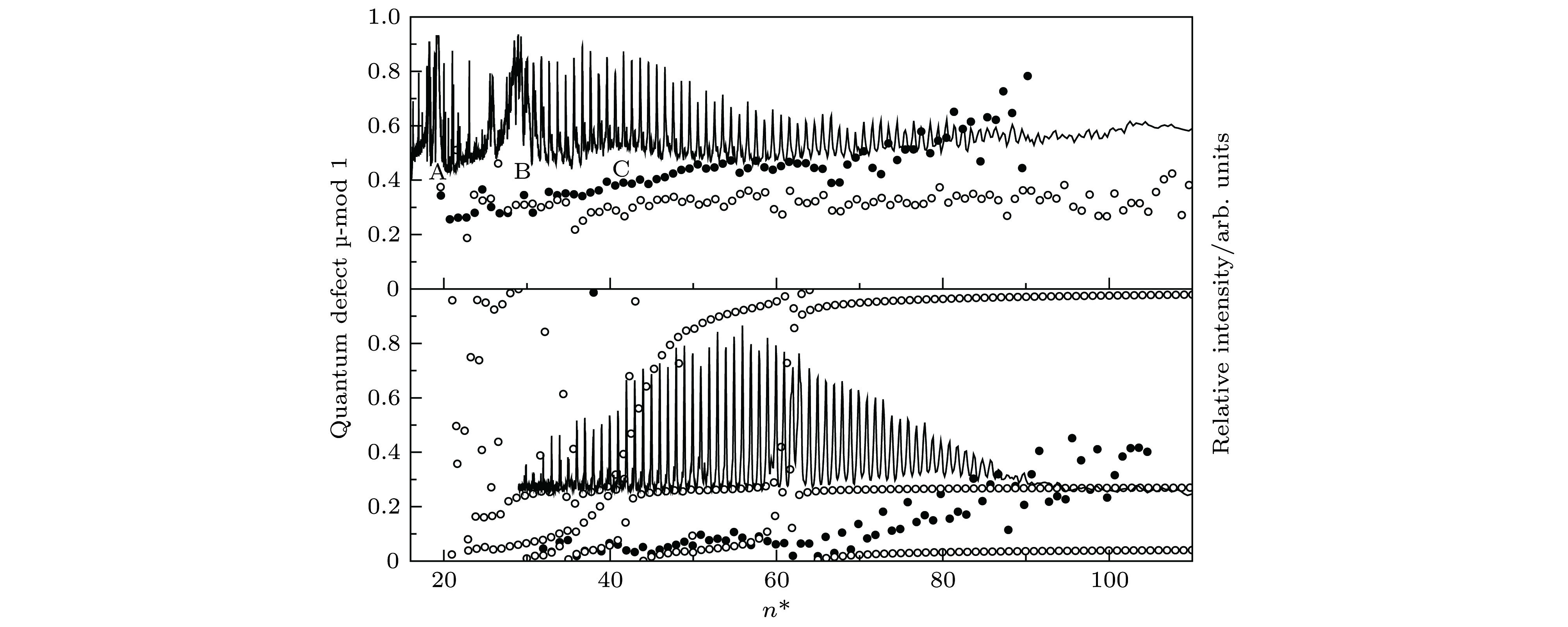
$ 5{\rm d}\epsilon {\rm p}\left(\dfrac{5}{2}, \dfrac{1}{2}\right)_3, J^\pi=3^- $ The theoretical spectrum shown in middle figure is obtained based on the Eq. (1), and included these eigenchannels with$ J^\pi=3^- $ :$ 5{\rm d}_{3/2}\epsilon {\rm f}_{5/2}$ ,$5{\rm d}_{5/2}\epsilon {\rm f}_{5/2}$ ,$5{\rm d}_{5/2}\epsilon {\rm p}_{1/2}$ ,$4{\rm f}_{5/2}\epsilon {\rm s}_{1/2}$ ,$4{\rm f}_{5/2}\epsilon {\rm d}_{3/2}$ ,$4{\rm f}_{7/2}\epsilon {\rm s}_{1/2}$ ,$4{\rm f}_{7/2}\epsilon {\rm d}_{3/2}$ ,$4{\rm f}_{7/2}\epsilon {\rm d}_{5/2} $ and$ 6{\rm p_{3/2}\epsilon d}_{5/2} $ .图 3 一价镧离子的里德伯系列(下图)和自电离里德伯系列(上图)对应的模为1的量子数亏损随激发能量的变化关系. 实验值用实心圆点表示, 理论计算给出了
$ J^\pi=3^- $ 的所有可能的束缚态能级和本征通道$ 5{\rm d}\epsilon {\rm p}\left(\dfrac{5}{2}, \dfrac{1}{2}\right)_3 $ 的谱峰能级对应的模为1的量子数亏损, 用空心圆点表示. 激发能量用有效量子数$ n^\star $ 表征, 利用了里德伯关系,$ E=E_\infty-\dfrac{Z^2 Ry.}{(n^\star)^2}, n^\star=n-\mu_{n, l, j} $ , 这里$ E $ 是激发能量,$ n^\star $ 为有效量子数,$ \mu $ 为量子数亏损,$ E_\infty $ 是相应的电离阈值,$ Z $ 为离子实的有效正电荷数,$ Ry. $ 为里德伯常数Fig. 3. Quantum defect
$ \mu $ mod 1 v.s. excited energy for Rydberg series(lower figure) and autoionization Rydberg series(upper figure) of La+.$ \bullet $ : Experimental data.$ \circ $ : theoretcal quantum defect mod 1 for all possible bound state energy levels with$ J^\pi=3^- $ symmetry and peak positions of eigenchannel$ 5{\rm d}\epsilon {\rm p}\left(\dfrac{5}{2}, \dfrac{1}{2}\right)_3 $ . Excitation energy is represented by the effective quantum number$ n^\star $ , according to Rydberg formula$ E=E_\infty-\dfrac{Z^2 Ry.}{(n^\star)^2}, n^\star=n-\mu $ . Here,$ E $ is excitation energy,$ n^\star $ is effective quantum number,$ \mu $ is quantum defect,$ E_\infty $ is the ionization threshold,$ Z $ is the charge of the ionic core, and$ Ry. $ is Rydberg constant.图 4 不同电离阈值得到的一价镧离子里德伯系列(有效量子数
$ n^\star>67 $ 时, 对应激发能量范围为90120 cm–1—90175 cm–1)量子数亏损随激发能量的变化关系. 采用文献[1]给出的一价镧离子第一电离阈值90212.8 cm–1, 得出的量子数亏损用实心圆点表示; 采用根据里德伯系列量子数亏损变化光滑性拟合的电离阈值90212.5 cm–1, 得出的量子数亏损用空心圆点表示Fig. 4. Quantum defect
$ \mu $ v.s. excited energy for the Rydberg series ($ n^\star>67 $ , in the energy region 90120 cm–1—90175 cm–1 ) converging to the different ionization thresholds.$ \bullet $ : quantum defects obtained by the ionization threshold 90212.8 cm–1 from Ref. [1].$ \circ $ : quantum defects obtained by the ionization threshold 90212.5 cm–1, which is fitted based on the quantum defect regular behavior for a Rydberg series.表 1 一价镧离子强自电离里德伯系列能级位置实验和理论比较. 理论标识分为两列: (1)本征通道
$ 5d\epsilon p\left(\dfrac{5}{2}, \dfrac{1}{2}\right)_3 $ , (2)本征通道$ 5d\epsilon p\left(\dfrac{5}{2}, \dfrac{1}{2}\right)_2 $ . 实验能级由中间态(Xe)$ 5{\rm d}6{\rm d} \; ^3{\rm{F}}_2 $ 激发的光谱得到. 实验误差为0.5 cm–1Table 1. Comparison of energy positions (cm–1) between the experimental and the theoretical strong autoionization Rydberg series of La+. Theoretical assignments are divided into two columns with the labels: (1) eigenchannel
$ 5d\epsilon p\left(\dfrac{5}{2}, \dfrac{1}{2}\right)_3 $ , (2) eigenchannel$ 5d\epsilon p\left(\dfrac{5}{2}, \dfrac{1}{2}\right)_2 $ . The experimental energy levels are obtained via the intermediate state (Xe)$ 5{\rm d}6{\rm d} \; ^3{\rm{F}}_2 $ . The experimental error is 0.5 cm–1.$ E_{{\rm{exp.}}} $ $ n^\star $ $ E_{{\rm{theo.}}} $ $ E_{{\rm{exp.}}} $ $ n^\star $ $ E_{{\rm{theo.}}} $ (1) (2) (1) (2) 90680.0 19.66 90676.4 90683.3 91678.8 56.56 91679.2 91679.5 90796.0 20.74 90777.4 90789.4 91683.4 57.53 91684.0 91684.1 90887.1 21.74 90865.5 90883.9 91688.0 58.55 91688.4 91688.5 90967.0 22.74 90972.6 90963.6 91692.3 59.56 91692.9 91692.7 91035.9 23.72 91031.5 91033.5 91696.3 60.55 91697.0 91696.8 91092.7 24.63 91095.1 91095.1 91700.1 61.53 91700.5 91700.6 91151.4 25.70 91149.8 91149.8 91703.8 62.54 91704.3 91704.1 91201.3 26.72 91192.8 91199.8 91707.3 63.54 91707.8 91707.8 91244.8 27.72 91244.4 91243.2 91710.7 64.56 91711.1 91711.1 91316.9 29.65 91318.1 91317.2 91713.9 65.56 91714.2 91714.2 91350.9 30.72 91349.9 91349.0 91717.1 66.61 91717.4 91717.3 91379.2 31.70 91379.2 91381.2 91720.0 67.61 91720.3 91720.2 91404.1 32.64 91405.3 91405.4 91722.6 68.54 91723.0 91722.9 91428.5 33.66 91428.9 91429.3 91725.2 69.52 91725.6 91725.6 91450.4 34.65 91451.1 91451.1 91727.7 70.49 91728.2 91728.2 91470.7 35.65 91473.2 91472.4 91730.3 71.55 91730.6 91730.5 91489.4 36.66 91491.0 91489.9 91732.7 72.58 91732.9 91732.9 91506.3 37.65 91507.5 91506.9 91734.7 73.47 91735.2 91735.2 91522.0 38.64 91523.2 91522.6 91737.0 74.53 91737.3 91737.3 91536.2 39.61 91537.5 91537.1 91739.0 75.49 91739.4 91739.3 91550.0 40.62 91551.2 91549.7 91741.0 76.49 91741.4 91741.4 91562.5 41.61 91564.0 91563.7 91742.8 77.42 91743.3 91743.2 91574.3 42.61 91575.3 91576.6 91744.8 78.50 91745.1 91745.0 91585.1 43.60 91585.9 91586.8 91746.5 79.45 91746.8 91746.9 91595.5 44.61 91596.3 91596.5 91748.2 80.44 91748.6 91748.6 91604.9 45.60 91605.6 91605.9 91749.7 81.35 91750.2 91750.2 91613.8 46.59 91614.5 91614.6 91751.4 82.41 91751.8 91751.8 91622.1 47.58 91622.8 91623.1 91752.9 83.39 91753.3 91753.3 91629.9 48.56 91630.8 91630.9 91754.6 84.53 91754.8 91754.8 91637.3 49.56 91638.1 91638.3 91755.8 85.37 91756.2 91756.2 91644.2 50.54 91645.2 91645.2 91757.2 86.38 91757.6 91757.6 91650.9 51.56 91651.7 91651.7 91758.4 87.27 91759.0 91758.9 91657.1 52.55 91657.8 91658.0 91759.8 88.35 91760.2 91760.2 91662.9 53.54 91663.8 91663.8 91761.3 89.56 91761.4 91761.5 91668.4 54.53 91669.2 91669.2 91762.1 90.22 91762.6 91762.6 91673.9 55.57 91674.3 91674.4 表 2 一价镧离子弱自电离里德伯系列能级位置实验和理论比较. 理论标识分为两列: (1)本征通道
$ 5d\epsilon f\left(\dfrac{5}{2}, \dfrac{5}{2}\right)_3 $ , (2)本征通道$ 5d\epsilon f\left(\dfrac{5}{2}, \dfrac{5}{2}\right)_2 $ . 实验能级由中间态(Xe)$ 5{\rm d}6{\rm d} \; ^3{\rm{F}}_2 $ 激发的光谱得到. 实验误差为0.5 cm–1Table 2. Comparison of energy positions (cm–1) between the experimental and the theoretical weak autoionization Rydberg series of La+. Theoretical assignments are divided into two columns with the labels: (1) eigenchannel
$ 5d\epsilon f\left(\dfrac{5}{2}, \dfrac{5}{2}\right)_3 $ , (2) eigenchannel$ 5d\epsilon f\left(\dfrac{5}{2}, \dfrac{5}{2}\right)_2 $ . The experimental energy levels are obtained via the intermediate state (Xe)$ 5{\rm d}6{\rm d} \; ^3{\rm{F}}_2 $ . The experimental error is 0.5 cm–1.$ E_{{\rm{exp.}}} $ $ n^\star $ $ E_{{\rm{theo.}}} $ $ E_{{\rm{exp.}}} $ $ n^\star $ $ E_{{\rm{theo.}}} $ (1) (2) (1) (2) 90980.9 22.93 90977.0 90981.4 91578.6 43.00 91576.0 91578.3 91317.2 29.66 91318.2 91326.2 91589.1 43.98 91586.1 91591.1 91359.7 31.01 91349.9 91357.1 91598.6 44.93 91596.8 91600.0 91387.7 32.01 91393.1 91386.0 91608.4 45.98 91606.2 91609.2 91412.1 32.97 91417.3 91411.5 91616.7 46.93 91615.2 91617.5 91435.4 33.96 91438.8 91436.8 91625.1 47.95 91623.5 91625.9 91456.7 34.95 91456.1 91457.6 91632.7 48.93 91631.2 91633.2 91474.6 35.86 91475.1 91478.1 91640.0 49.94 91641.5 91640.6 91494.6 36.95 91492.7 91495.9 91646.8 50.93 91645.6 91647.4 91511.1 37.94 91508.9 91512.3 91653.3 51.94 91651.9 91653.9 91526.2 38.92 91523.0 91527.7 91659.3 52.92 91658.2 91660.1 91541.4 39.98 91538.7 91541.6 91665.0 53.91 91664.1 91665.7 91554.8 40.99 91552.1 91554.8 91670.2 54.86 91669.4 91671.1 91567.1 41.99 91564.4 91566.9 91675.5 55.89 91674.7 91676.1 -
[1] Xie X P, Xu C B, Sun W, Xue P, Zhong Z P, Huang W, Xu X Y 1999 J. Opt. Soc. Am. B 16 484
 Google Scholar
Google Scholar
[2] Kramida A, Ralchenko Y, Reader J, Team, NIST A S D url: https://physics.nist.gov/asd [2018-12-1]
[3] Fano U 1970 Phys. Rev. A 2 353
 Google Scholar
Google Scholar
[4] Lee C M, Lu K T 1973 Phys. Rev. A 8 1241
 Google Scholar
Google Scholar
[5] Greene C, Fano U, Strinati G 1979 Phys. Rev. A 19 1485
 Google Scholar
Google Scholar
[6] Johnson W R, Lin C D, Cheng K T, Lee C M 1980 Phys. Scr. 21 409
 Google Scholar
Google Scholar
[7] 李家明 1980 29 419
 Google Scholar
Google Scholar
Li J M 1980 Acta Phys. Sin. 29 419
 Google Scholar
Google Scholar
[8] Seaton M J 1983 Rep. Prog. Phys. 46 167
 Google Scholar
Google Scholar
[9] 李家明 1983 32 84
 Google Scholar
Google Scholar
Li J M 1983 Acta Phys. Sin. 32 84
 Google Scholar
Google Scholar
[10] Lee C M 1974 Phys. Rev. A 10 584
 Google Scholar
Google Scholar
[11] 邹宇, 仝晓民, 李家明 1995 44 50
 Google Scholar
Google Scholar
Zou Y, Tong X M, Li J M 1995 Acta Phys. Sin. 44 50
 Google Scholar
Google Scholar
[12] Huang W, Zou Y, Tong X M, Li J M 1995 Phys. Rev. A 52 2770
 Google Scholar
Google Scholar
[13] 颜君, 张培鸿, 仝晓民, 李家明 1996 45 1978
 Google Scholar
Google Scholar
Yan J, Zhang P H, Tong X M, Li J M 1996 Acta Phys. Sin. 45 1978
 Google Scholar
Google Scholar
[14] Li J M, Wu Y J, Pratt R H 1989 Phys. Rev. A 40 3036
 Google Scholar
Google Scholar
[15] Xia D, Li J M 2001 Chin. Phys. Lett. 18 1334
 Google Scholar
Google Scholar
[16] Xia D, Zhang S Z, Peng Y L, Li J M 2003 Chin. Phys. Lett. 20 56
 Google Scholar
Google Scholar
[17] Sun W, Yan J, Zhong Z P, Xie X P, Xue P, Xu X Y 2001 J. Phys. B: At. Mol. Opt. Phys. 34 369
 Google Scholar
Google Scholar
[18] Zhang X F, Jia F D, Zhong Z P, Xue P, Xu X Y, Yan J 2007 Chin. Phys. Lett. 24 2808
 Google Scholar
Google Scholar
[19] Wang J Y, Zhong Z P, Jia F D, Qu Y Z, Zhong Y P 2008 J. Phys. B: At. Mol. Opt. Phys. 41 085002
 Google Scholar
Google Scholar
[20] Zhong Y P, Jia F D, Zhong Z P 2009 Chin. Phys. B 18 4242
 Google Scholar
Google Scholar
[21] Sedlacek J A, Schwettmann A, Kübler H, Löw R, Pfau T, Shaffer J P 2012 Nat. Phys. 8 819
 Google Scholar
Google Scholar
[22] 黄巍, 梁振涛, 杜炎雄, 颜辉, 朱诗亮 2015 64 160702
 Google Scholar
Google Scholar
Huang W, Liang Z T, Du Y X, Yan H, Zhu S L 2015 Acta Phys. Sin. 64 160702
 Google Scholar
Google Scholar
[23] 孙玮 2001 博士学位论文 (北京: 清华大学)
Sun W 2001 Ph. D. Dissertation (Beijing: Tsinghua University) (in Chinese)
[24] Huang W, Xu X Y, Xu C B, Xue M, Chen D Y 1995 J. Opt. Soc. Am. B 12 961
 Google Scholar
Google Scholar
[25] Huang W, Xu X Y, Xu C B, Xue M, Li L Q, Chen D Y 1994 Phy. Rev. A 49 R653
 Google Scholar
Google Scholar
[26] 赵中新, 李家明 1985 34 1469
 Google Scholar
Google Scholar
Zhao Z X, Li J M 1985 Acta Phys. Sin. 34 1469
 Google Scholar
Google Scholar
[27] 李心梅, 阮亚平, 钟志萍 2012 61 023104
 Google Scholar
Google Scholar
Li X M, Ruan Y P, Zhong Z P 2012 Acta Phys. Sin. 61 023104
 Google Scholar
Google Scholar
[28] Jia F D, Zhong Z P, Sun W, Xue P, Xu X Y 2009 Phys. Rev. A 79 032505
 Google Scholar
Google Scholar
[29] Lv S F, Li R, Jia F D, Li X K, Lassen J, Zhong Z P 2017 Chin. Phys. Lett. 34 073101
 Google Scholar
Google Scholar
[30] Li R, Lassen J, Zhong Z P, Jia F D, Mostamand M, Li X K, Reich B B, Teigelhöfer A, Yan H 2017 Phy. Rev. A 95 052501
 Google Scholar
Google Scholar
[31] Gallagher T F 1994 Rydberg Atom (1st Ed.) (Cambridge: Cambridge University Press) pp 70–102
[32] Ecker G, Kröll W 1963 Phys. Fluids 6 62
 Google Scholar
Google Scholar
[33] Stewart J C, Pyatt Jr. K D 1966 Astrophys. J. 144 1203
 Google Scholar
Google Scholar
[34] Qi Y Y, Wang J G, Janev R K 2008 Phys. Rev. A 78 062511
 Google Scholar
Google Scholar
[35] Lyon M, Rolston S L 2017 Rep. Prog. Phys. 80 017001
 Google Scholar
Google Scholar
[36] Park H, Ali R, Gallagher T F 2010 Phys. Rev. A 82 023421
 Google Scholar
Google Scholar
计量
- 文章访问数: 10052
- PDF下载量: 79
- 被引次数: 0





























 下载:
下载: