-
利用“二态矢量模型”详细研究了高电荷态
${\rm{O}}^{7+}$ ,${\rm{N}}^{6+}$ 离子入射Al表面时中间里德伯态的形成过程, 给出了电子被俘获至不同量子数$\left(n_{{\rm{A}}}=2-7\right)$ 的几率, 以及电子俘获至里德伯态最可能的离子-表面距离. 计算结果表明, 较大的主量子数$n_{\rm A}$ 对应较小的里德伯态几率, 因此${\rm{O}}^{7+}$ ,${\rm{N}}^{6+}$ 离子入射Al表面时辐射的X射线主要来源于较小的$n_{{\rm{A}}}$ 至基态的退激. 为了验证计算结果, 测量了${\rm{O}}^{7+}$ ,${\rm{N}}^{6+}$ 离子入射Al 表面的X射线发射谱, 并运用FAC程序计算了不同高里德伯态退激到基态的跃迁能(np–1s). 实验测量到O, N 的K-X射线峰, 其特征峰的中心值接近主量子数n = 2至n = 1的跃迁能, 说明发射的X 射线主要来源于2p–1s的跃迁, 与“二态矢量模型”理论计算的几率一致.The study of the interaction between highly charged ions and solid surfaces not only has great significance for basic scientific research such as atomic physics, astrophysics, and high energy density physics but also has promising application prospects in biomedicine, nanotechnology, surface analysis, and microelectronics. In this paper, the intermediate Rydberg states formed during highly charged${\rm{O}}^{7+}$ and${\rm{N}}^{6+}$ ions incident on Al surface are studied theoretically by using the two-state vector model. Both the probability of electron capture into different Rydberg states$\left(n_{A}=2-7\right)$ and the most probable neutralization distances are given. The calculation shows that the larger principal quantum number$n_{A}$ is relevant to smaller probability. Therefore, the X-rays emitted by${\rm{O}}^{7+}$ and${\rm{N}}^{6+}$ ions incident on the Al surface come mainly from the de-excitation of the smaller$n_{A}$ to the ground state. In order to confirm the calculations, we measured the X-ray emission spectra of${\rm{O}}^{7+}$ and${\rm{N}}^{6+}$ ions in collisions with the Al surface in the energy range of 3–20 keV/q. The experiments were performed at an ECR ion source located in Institute of modern physics. We also calculated the transition energies (np–1s) from different high Rydberg states to the ground state by using the FAC code. The center of the measured K X-ray peak is close to the calculated transition energy from the principal quantum number n = 2 to n = 1, it is consistent with our results obtained by the two-state vector model as well. In addition, we found the experimental K X-ray yield for${\rm{O}}^{7+}$ ions incidence at lower energy collisions is almost the same with${\rm{N}}^{6+}$ ions, but larger at higher energy collisions. When the ion incident kinetic energy is low, the X-ray emission is mainly owing to the decay of “above the surface” hollow atoms. Because of the small difference in the critical distances for the capture of electrons by${\rm{O}}^{7+}$ and${\rm{N}}^{6+}$ to form hollow atoms, the X-ray yields produced in both cases are almost the same at low energy collisions. In contrast, as increasing the incident energy, the ions have a long-range in the target, so the contribution from the decay of “above the surface” and “below the surface” hollow atoms need to be considered at the same time.-
Keywords:
- highly charged ions /
- Rydberg states /
- the two-state vector model /
- X-rays
[1] Arnau A, Aumayr F, Echenique P M, Grether M, Heiland W, Limburg J, Morgenstern R, Roncin P, Schippers S, Schuch R, Stolterfoht N, Varga P, Zouros T J M, Winter H 1997 Surf. Sci. Rep. 27 113
Google Scholar
[2] Schenkel T, Hamza A V, Barnes A V, Schneider D H 1999 Prog. Surf. Sci. 61 23
Google Scholar
[3] Winter H, Aumayr F 1999 J. Phys. B: At. Mol. Opt. Phys. 3 2
[4] Song Z Y, Yang Z H, Xiao G Q, Xu Q M, Chen J, Yang B, Yang Z R 2011 Eur. Phys. J. D 64 197
Google Scholar
[5] Zhao Y T, Xiao G Q, Zhang X A, Yang Z H, Zhan W L, Chen X M, Li F L 2006 Nucl. Instrum. Methods Phys. Res., Sect. B 245 72
Google Scholar
[6] Zhao Y T, Xiao G Q, Zhang X A, Yang Z H, Zhang Y P, Zhan W L, Chen X M, Li F L 2007 Nucl. Instrum. Methods Phys. Res., Sect. B 258 121
Google Scholar
[7] 张小安, 梅策香, 张颖, 梁昌慧, 周贤明, 曾利霞, 李耀宗, 柳钰, 向前兰, 孟惠, 王益军 2020 69 213301
Google Scholar
Zhang X A, Mei C X, Zhang Y, Liang C H, Zhou X M, Zeng L X, Li Y Z, Liu Y, Xiang Q L, Meng H, Wang Y J 2020 Acta Phys. Sin. 69 213301
Google Scholar
[8] Lei Y, Cheng R, Zhou X M, Wang X, Wang Y Y, Ren J R, Zhao Y T, Ma X W, Xiao G Q 2018 Eur. Phys. J. D 72 132
Google Scholar
[9] 张小安, 李耀宗, 赵永涛, 梁昌慧, 程锐, 周贤明, 王兴, 雷瑜, 孙渊博, 徐戈, 李锦玉, 肖国青 2012 61 113401
Google Scholar
Zhang X A, Li Y Z, Zhao Y T, Liang C H, Cheng R, Zhou X M, Wang X, Lei Y, Sun Y B, Xu G, Li J Y, Xiao G Q 2012 Acta Phys. Sin. 61 113401
Google Scholar
[10] Zhang H, Chen X, Yang Z, Xu J, Cui Y, Shao J, Zhang X, Zhao Y, Zhang Y, Xiao G 2010 Nucl. Instrum. Methods Phys. Res., Sect. B 268 1564
Google Scholar
[11] Nedeljković L D, Nedeljković N N, Božanić D K 2006 Phys. Rev. A 74 032901
Google Scholar
[12] Borisov A G, Zimny R, Teillet-Billy D, Gauyacq J P 1996 Phys. Rev. A 53 2457
Google Scholar
[13] Burgdörfer J, Lerner P, Meyer F W 1991 Phys. Rev. A 44 5674
Google Scholar
[14] Iwai Y, Murakoshi D, Kanai Y, Oyama H, Ando K, Masuda H, Nishio K, Nakao M, Tamamura T, Komaki K, Yamazaki Y 2002 Nucl. Instrum. Methods Phys. Res., Sect. B 193 504
Google Scholar
[15] Kanai Y, Nakai Y, Iwai Y, Ikeda T, Hoshino M, Nishio K, Masuda H, Yamazaki Y 2005 Nucl. Instrum. Methods Phys. Res., Sect. B 233 103
Google Scholar
[16] Tökési K, Wirtz L, Lemell C, Burgdörfer J 2000 Phys. Rev. A 61 020901
Google Scholar
[17] Ninomiya S, Yamazaki Y, Koike F, Masuda H, Azuma T, Komaki K, Kuroki K, Sekiguchi M 1997 Phys. Rev. Lett. 78 4557
Google Scholar
[18] Ninomiya S, Yamazaki Y, Azuma T, Komaki K, Koike F, Masuda H, Kuroki K, Sekiguchi M 1997 Phys. Scr. T73 316
Google Scholar
[19] Aumayr F, Kurz H, Schneider D, Briere M A, McDonald J W, Cunningham C E, Winter H 1993 Phys. Rev. Lett. 71 1943
Google Scholar
[20] Song Z Y, Yang Z H, Zhang H Q, Shao J X, Cui Y, Zhang Y P, Zhang X A, Zhao Y T, Chen X M, Xiao G Q 2015 Phys. Rev. A 91 042707
Google Scholar
[21] Nedeljković N N, Majkić M D 2007 Phys. Rev. A 76 042902
Google Scholar
[22] Nedeljković N N, Nedeljković L D, Mirković M A 2003 Phys. Rev. A 68 012721
Google Scholar
[23] Gillaspy J D, Pomeroy J M, Perrella A C, Grube H 2007 J. Phys. Conf. Ser. 58 451
Google Scholar
[24] Tona M, Watanabe H, Takahashi S, Nakamura N, Yoshiyasu N, Sakurai M, Terui T, Mashiko S, Yamada C, Ohtani S 2007 Nucl. Instrum. Methods Phys. Res., Sect. B 256 543
Google Scholar
[25] Heller R, Facsko S, Wilhelm R A, Moller W 2008 Phys. Rev. Lett. 101 096102
Google Scholar
[26] El-Said A S, Wilhelm R A, Heller R, Facsko S, Lemell C, Wachter G, Burgdorfer J, Ritter R, Aumayr F 2012 Phys. Rev. Lett. 109 117602
Google Scholar
[27] Nedeljković N N, Majkić M D, Božanić D K, Dojčilović R J 2016 J. Phys. B: At. Mol. Opt. Phys. 49 125201
Google Scholar
[28] Nedeljković N N, Majkić M D, Galijaš S M D 2012 J. Phys. B: At. Mol. Opt. Phys. 45 215202
Google Scholar
[29] Kramida A, Ralchenko Y, Reader J, NIST ASD Team 2021 NIST Atomic Spectra Database [EB/OL] https://physics.nist.gov/asd [2021-12-27]
[30] 张秉章, 宋张勇, 刘璇, 钱程, 方兴, 邵曹杰, 王伟, 刘俊亮, 徐俊奎, 冯勇, 朱志超, 郭艳玲, 陈林, 孙良亭, 杨治虎, 于得洋 2021 70 193201
Google Scholar
Zhang B Z, Song Z Y, Liu X, Qian C, Fang X, Shao C J, Wang W, Liu J L, Xu J K, Feng Y, Zhu Z C, Guo Y L, Chen L, Sun L T, Yang Z H, Yu D Y 2021 Acta Phys. Sin. 70 193201
Google Scholar
-
图 1
$ {\rm{O}}^{7+} $ 离子俘获电子至里德伯态$v_{{\rm{A}}}(n_{{\rm{A}}}=3 ; \; l_{{\rm{A}}}= $ $ 0, 1, 2, 3)$ 的几率, 其中$l_{{\rm{A}}}=2$ 和$l_{{\rm{A}}}=3$ 的几率相等. 虚线对应点状核模型Fig. 1. Probability for the
$ {\rm{O}}^{7+} $ ion capturing an electron into the Rydberg states$\left(n_{{\rm{A}}}=3 ;\; l_{{\rm{A}}}=0, 1, 2, 3\right)$ , where the values of$l_{{\rm{A}}}=2$ and$l_{{\rm{A}}}=3$ are equal. Dashed curves correspond to the case of the pointlike core
图 2 电子被俘获至不同里德堡态
$\left(n_{{\rm{A}}} = 2 - 7\right)$ 的几率 (a)${\rm{O}} ^{7 + } $ 离子; (b)$ {\rm{N}}^{6 + } $ 离子Fig. 2. Probability for the electron captured into the Rydberg states
$ \left(n_{{\rm{A}}} = 2 - 7\right) $ : (a)$ {\rm{O}}^{7 + } $ ion; (b)$ {\rm{N}}^{6 + } $ ion
图 3
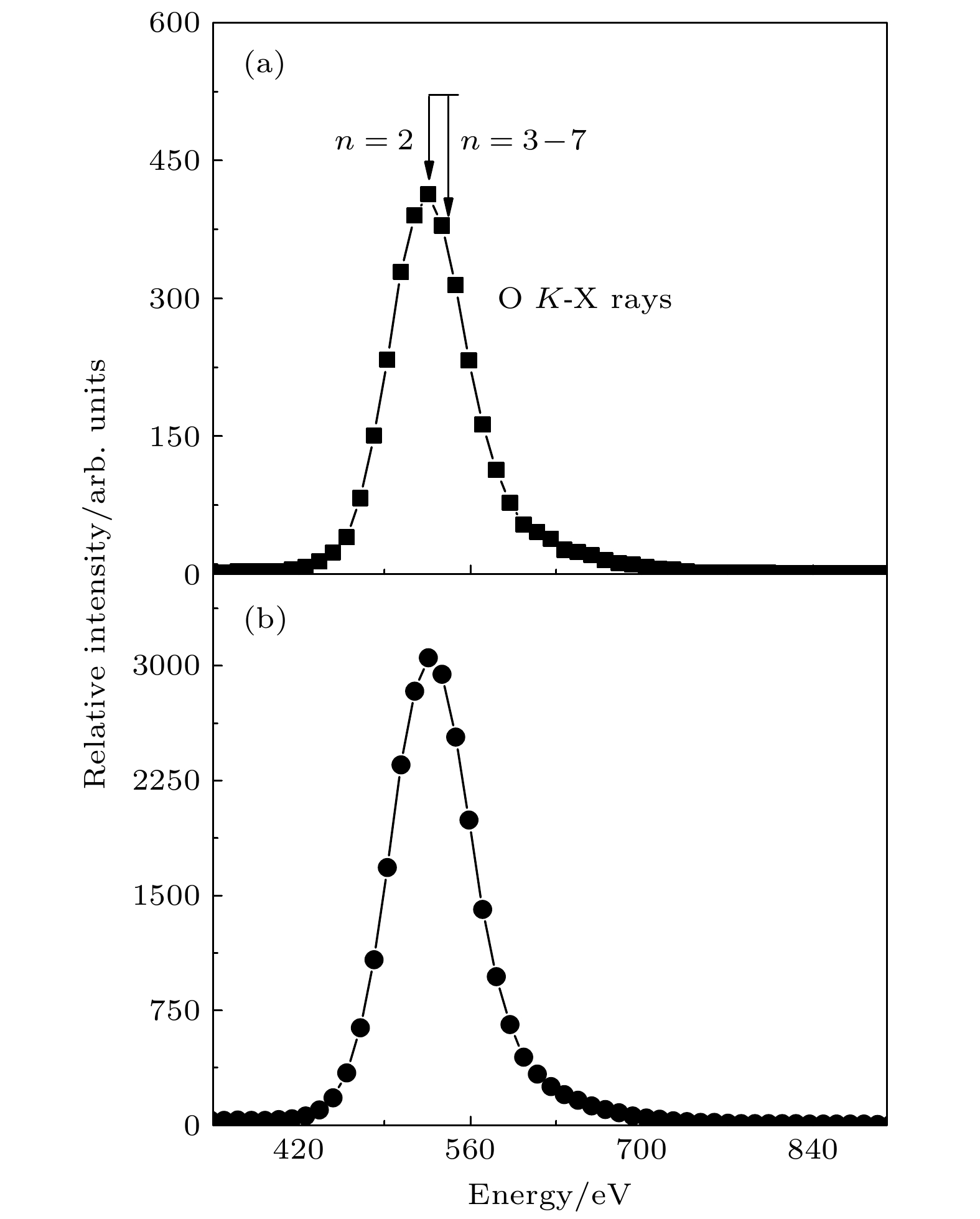
$ {\rm{O}}^{7 + } $ 离子入射Al表面发射的X射线谱, 其中(a)为3 keV/q, (b) 为20 keV/q. 图中箭头标示了FAC程序计算的不同里德堡态退激到基态的跃迁能Fig. 3. X-ray spectra induced by
${\rm{O}} ^{7 + } $ ions impact on aluminum surfaces at (a) 3 keV/q and (b) 20 keV/q collisional energy. The arrows indicate the calculated X-ray energies for different Rydberg states to the ground state by FAC code
图 4
${\rm{N}} ^{6 + } $ 离子入射Al表面发射的X射线谱, 其中(a)为3 keV/q, (b) 为20 keV/q. 图中箭头标示了FAC程序计算的不同里德堡态退激到基态的跃迁能Fig. 4. X-ray spectra generated by
$ {\rm{N}}^{6 + } $ ions incident on aluminum surfaces at (a) 3 keV/q and (b) 20 keV/q collisional energy. The arrows indicate the calculated X-ray energies for different Rydberg states to the ground state by FAC code
图 5 3—20 keV/q的
${\rm{O}} ^{7 + } $ ,${\rm{N}} ^{6 + } $ 离子入射Al表面的X射线产额Fig. 5. X-ray yield by the bombardment of
$ {\rm{O}}^{7 + } $ and$ {\rm{N}}^{6 + } $ ions on aluminium surface with 3-20 keV/q incident energies.表 1
${\rm{O}}^{7 + }$ ,${\rm{N}}^{6 + }$ 离子在考虑离子极化下的能级参数$\widetilde{\gamma}_{{\rm{A}}}$ (arb. units), 及不考虑离子极化下的参数$\gamma_{{\rm{A}} 0}= $ $ Z / n_{{\rm{A}}}$ (arb. units)Table 1. Energy parameter
$\widetilde{\gamma}_{{\rm{A}}}$ (arb. units) and$\gamma_{{\rm{A}} 0} = $ $ Z / n_{\rm A}$ (arb. units) for the ions${\rm{O}}^{7 + }$ and${\rm{N}}^{6 + }$ , separately correspond to the cases with and without polarization of the ionic core$n_{{\rm{A}}}$ $l_{{\rm{A}}} = 0$ $l_{{\rm{A}}} = 1$ $l_{{\rm{A}}} = 2$ $l_{{\rm{A}}} = 3$ $\gamma_{{\rm{A}} 0}$ ${\rm{O} }^{7 + }({{Z} } = 7)$ 2 3.540 3.487 3.500 3 2.352 2.328 2.334 2.334 2.333 4 1.760 1.748 1.751 1.751 1.750 5 1.399 1.400 1.401 1.400 6 1.166 1.167 1.168 1.167 7 1.003 1.000 ${\rm{N} }^{6+}({{Z} }=6)$ 2 3.040 2.987 3.000 3 2.018 1.994 2.000 2.000 4 1.510 1.497 1.500 1.500 5 1.207 1.195 1.200 1.200 6 0.999 1.000 7 0.855 0.857 
下载: 导出CSV
表 2 TVM模型计算的
${\rm{O}}^{7 + }$ ,${\rm{N}}^{6 + }$ 离子的中和距离. 括号中的值代表点状核模型的中和距离Table 2. The neutralization distances for the
${\rm{O}}^{7 + }$ and${\rm{N}}^{6 + }$ ions calculated by TVM. Numbers in parentheses are the neutralization distances for the pointlike ionic core case$n_{{\rm{A}}}$ $l_{{\rm{A}}}=0$ $l_{{\rm{A}}}=1$ $l_{{\rm{A}}}=2$ $l_{{\rm{A}}}=3$ ${\rm{O}}^{7 + }$ 2 1.27 (1.28) 1.28 (1.28) (1.28) (1.28) 3 2.68 (2.74) 2.75 (2.74) 2.69 (2.74) 2.69 (2.74) 4 4.60 (4.62) 4.63 (4.62) 4.62 (4.62) 4.62 (4.62) 5 (7.01) 7.02 (7.01) 7.01 (7.01) 7.01 (7.01) 6 (9.87) 9.88 (9.87) 9.87 (9.87) 9.81 (9.87) 7 (13.30) 13.21(13.30) (13.30) (13.30) ${\rm{N}}^{6+}$ 2 1.45 (1.51) 1.52 (1.51) (1.51) (1.51) 3 3.15 (3.18) 3.18 (3.18) 3.18 (3.18) (3.18) 4 5.36 (5.39) 5.45 (5.39) 5.39 (5.39) (5.39) 5 8.13 (8.22) 8.25 (8.22) 8.22 (8.22) (8.22) 6 (11.65) 11.66 (11.65) (11.65) (11.65) 7 (16.29) 16.37 (16.29) (16.29) (16.29)
下载: 导出CSV
表 3 基于FAC程序计算的不同高里德堡态退激到基态的跃迁能(np −1s)
Table 3. Calculated transition energy for different Rydberg states to the ground state using FAC code (np −1s)
O ion $2 {\rm{p}}-1 {\rm{s}}$ $3{\rm{ p}}-1{\rm{ s}}$ $4 {\rm{p}}-1{\rm{ s}}$ $5 {\rm{p}}-1{\rm{ s}}$ $6 {\rm{p}}-1 {\rm{s}}$ $7 {\rm{p}}-1 {\rm{s}}$ Energy/eV 526.4 541.5 543.5 543.9 544.1 544.2 N ion $2 {\rm{p}}-1 {\rm{s}}$ $3 {\rm{p}}-1 {\rm{s}}$ $4 {\rm{p}}-1 {\rm{s}}$ $5 {\rm{p}}-1{\rm{ s}}$ $6 {\rm{p}}-1 {\rm{s}}$ $7 {\rm{p}}-1 {\rm{s}}$ Energy/eV 395.8 407.8 409.7 410.1 410.3 410.4
下载: 导出CSV
-
[1] Arnau A, Aumayr F, Echenique P M, Grether M, Heiland W, Limburg J, Morgenstern R, Roncin P, Schippers S, Schuch R, Stolterfoht N, Varga P, Zouros T J M, Winter H 1997 Surf. Sci. Rep. 27 113
Google Scholar
[2] Schenkel T, Hamza A V, Barnes A V, Schneider D H 1999 Prog. Surf. Sci. 61 23
Google Scholar
[3] Winter H, Aumayr F 1999 J. Phys. B: At. Mol. Opt. Phys. 3 2
[4] Song Z Y, Yang Z H, Xiao G Q, Xu Q M, Chen J, Yang B, Yang Z R 2011 Eur. Phys. J. D 64 197
Google Scholar
[5] Zhao Y T, Xiao G Q, Zhang X A, Yang Z H, Zhan W L, Chen X M, Li F L 2006 Nucl. Instrum. Methods Phys. Res., Sect. B 245 72
Google Scholar
[6] Zhao Y T, Xiao G Q, Zhang X A, Yang Z H, Zhang Y P, Zhan W L, Chen X M, Li F L 2007 Nucl. Instrum. Methods Phys. Res., Sect. B 258 121
Google Scholar
[7] 张小安, 梅策香, 张颖, 梁昌慧, 周贤明, 曾利霞, 李耀宗, 柳钰, 向前兰, 孟惠, 王益军 2020 69 213301
Google Scholar
Zhang X A, Mei C X, Zhang Y, Liang C H, Zhou X M, Zeng L X, Li Y Z, Liu Y, Xiang Q L, Meng H, Wang Y J 2020 Acta Phys. Sin. 69 213301
Google Scholar
[8] Lei Y, Cheng R, Zhou X M, Wang X, Wang Y Y, Ren J R, Zhao Y T, Ma X W, Xiao G Q 2018 Eur. Phys. J. D 72 132
Google Scholar
[9] 张小安, 李耀宗, 赵永涛, 梁昌慧, 程锐, 周贤明, 王兴, 雷瑜, 孙渊博, 徐戈, 李锦玉, 肖国青 2012 61 113401
Google Scholar
Zhang X A, Li Y Z, Zhao Y T, Liang C H, Cheng R, Zhou X M, Wang X, Lei Y, Sun Y B, Xu G, Li J Y, Xiao G Q 2012 Acta Phys. Sin. 61 113401
Google Scholar
[10] Zhang H, Chen X, Yang Z, Xu J, Cui Y, Shao J, Zhang X, Zhao Y, Zhang Y, Xiao G 2010 Nucl. Instrum. Methods Phys. Res., Sect. B 268 1564
Google Scholar
[11] Nedeljković L D, Nedeljković N N, Božanić D K 2006 Phys. Rev. A 74 032901
Google Scholar
[12] Borisov A G, Zimny R, Teillet-Billy D, Gauyacq J P 1996 Phys. Rev. A 53 2457
Google Scholar
[13] Burgdörfer J, Lerner P, Meyer F W 1991 Phys. Rev. A 44 5674
Google Scholar
[14] Iwai Y, Murakoshi D, Kanai Y, Oyama H, Ando K, Masuda H, Nishio K, Nakao M, Tamamura T, Komaki K, Yamazaki Y 2002 Nucl. Instrum. Methods Phys. Res., Sect. B 193 504
Google Scholar
[15] Kanai Y, Nakai Y, Iwai Y, Ikeda T, Hoshino M, Nishio K, Masuda H, Yamazaki Y 2005 Nucl. Instrum. Methods Phys. Res., Sect. B 233 103
Google Scholar
[16] Tökési K, Wirtz L, Lemell C, Burgdörfer J 2000 Phys. Rev. A 61 020901
Google Scholar
[17] Ninomiya S, Yamazaki Y, Koike F, Masuda H, Azuma T, Komaki K, Kuroki K, Sekiguchi M 1997 Phys. Rev. Lett. 78 4557
Google Scholar
[18] Ninomiya S, Yamazaki Y, Azuma T, Komaki K, Koike F, Masuda H, Kuroki K, Sekiguchi M 1997 Phys. Scr. T73 316
Google Scholar
[19] Aumayr F, Kurz H, Schneider D, Briere M A, McDonald J W, Cunningham C E, Winter H 1993 Phys. Rev. Lett. 71 1943
Google Scholar
[20] Song Z Y, Yang Z H, Zhang H Q, Shao J X, Cui Y, Zhang Y P, Zhang X A, Zhao Y T, Chen X M, Xiao G Q 2015 Phys. Rev. A 91 042707
Google Scholar
[21] Nedeljković N N, Majkić M D 2007 Phys. Rev. A 76 042902
Google Scholar
[22] Nedeljković N N, Nedeljković L D, Mirković M A 2003 Phys. Rev. A 68 012721
Google Scholar
[23] Gillaspy J D, Pomeroy J M, Perrella A C, Grube H 2007 J. Phys. Conf. Ser. 58 451
Google Scholar
[24] Tona M, Watanabe H, Takahashi S, Nakamura N, Yoshiyasu N, Sakurai M, Terui T, Mashiko S, Yamada C, Ohtani S 2007 Nucl. Instrum. Methods Phys. Res., Sect. B 256 543
Google Scholar
[25] Heller R, Facsko S, Wilhelm R A, Moller W 2008 Phys. Rev. Lett. 101 096102
Google Scholar
[26] El-Said A S, Wilhelm R A, Heller R, Facsko S, Lemell C, Wachter G, Burgdorfer J, Ritter R, Aumayr F 2012 Phys. Rev. Lett. 109 117602
Google Scholar
[27] Nedeljković N N, Majkić M D, Božanić D K, Dojčilović R J 2016 J. Phys. B: At. Mol. Opt. Phys. 49 125201
Google Scholar
[28] Nedeljković N N, Majkić M D, Galijaš S M D 2012 J. Phys. B: At. Mol. Opt. Phys. 45 215202
Google Scholar
[29] Kramida A, Ralchenko Y, Reader J, NIST ASD Team 2021 NIST Atomic Spectra Database [EB/OL] https://physics.nist.gov/asd [2021-12-27]
[30] 张秉章, 宋张勇, 刘璇, 钱程, 方兴, 邵曹杰, 王伟, 刘俊亮, 徐俊奎, 冯勇, 朱志超, 郭艳玲, 陈林, 孙良亭, 杨治虎, 于得洋 2021 70 193201
Google Scholar
Zhang B Z, Song Z Y, Liu X, Qian C, Fang X, Shao C J, Wang W, Liu J L, Xu J K, Feng Y, Zhu Z C, Guo Y L, Chen L, Sun L T, Yang Z H, Yu D Y 2021 Acta Phys. Sin. 70 193201
Google Scholar
-
[1] 刘鑫, 汶伟强, 李冀光, 魏宝仁, 肖君. 高电荷态类硼离子2P3/2 — 2P1/2跃迁的实验和理论研究进展. , 2024, 73(20): 203102. doi: 10.7498/aps.73.20241190 [2] 吴怡娇, 孟天鸣, 张献文, 谭旭, 马蒲芳, 殷浩, 任百惠, 屠秉晟, 张瑞田, 肖君, 马新文, 邹亚明, 魏宝仁. 高电荷态Ar8+离子与He原子碰撞中双电子俘获量子态选择截面实验研究. , 2024, 73(24): . doi: 10.7498/aps.73.20241290 [3] 史路林, 程锐, 王昭, 曹世权, 杨杰, 周泽贤, 陈燕红, 王国东, 惠得轩, 金雪剑, 吴晓霞, 雷瑜, 王瑜玉, 苏茂根. 近玻尔速度能区高电荷态离子与激光等离子体相互作用实验研究装置. , 2023, 72(13): 133401. doi: 10.7498/aps.72.20230214 [4] 张大成, 葛韩星, 巴雨璐, 汶伟强, 张怡, 陈冬阳, 汪寒冰, 马新文. 高电荷态离子阿秒激光光谱研究展望. , 2023, 72(19): 193201. doi: 10.7498/aps.72.20230986 [5] 张秉章, 宋张勇, 张明武, 刘璇, 钱程, 方兴, 邵曹杰, 王伟, 刘俊亮, 朱志超, 孙良亭, 于得洋. 类氢O、N离子入射Al表面俘获电子布居几率的理论与实验研究. , 2022, 0(0): 0-0. doi: 10.7498/aps.71.20212434 [6] 张秉章, 宋张勇, 刘璇, 钱程, 方兴, 邵曹杰, 王伟, 刘俊亮, 徐俊奎, 冯勇, 朱志超, 郭艳玲, 陈林, 孙良亭, 杨治虎, 于得洋. 低能高电荷态 ${\boldsymbol{ {\rm{O}}^{q+}}}$ 离子与Al表面作用产生的X射线. , 2021, 70(19): 193201. doi: 10.7498/aps.70.20210757[7] 李晓康, 贾凤东, 余方晨, 李明阳, 薛平, 许祥源, 钟志萍. 一价镧离子高n里德伯态. , 2019, 68(4): 043201. doi: 10.7498/aps.68.20181980 [8] 裴栋梁, 何军, 王杰英, 王家超, 王军民. 铯原子里德伯态精细结构测量. , 2017, 66(19): 193701. doi: 10.7498/aps.66.193701 [9] 梁昌慧, 张小安, 李耀宗, 赵永涛, 梅策香, 周贤明, 肖国青. 不同电荷态的129Xeq+激发Au的X射线发射研究. , 2015, 64(5): 053201. doi: 10.7498/aps.64.053201 [10] 孙江, 孙娟, 王颖, 苏红新. 双光子共振非简并四波混频测量Ba原子里德伯态的碰撞展宽和频移. , 2012, 61(11): 114214. doi: 10.7498/aps.61.114214 [11] 孙江, 刘鹏, 孙娟, 苏红新, 王颖. 双光子共振非简并四波混频测量钡原子里德伯态碰撞展宽中的伴线研究. , 2012, 61(12): 124205. doi: 10.7498/aps.61.124205 [12] 邹贤容, 邵剑雄, 陈熙萌, 崔莹. 高电荷态Ar17+离子在表面以下过程中发射X射线分支比及各分支能量的研究. , 2010, 59(9): 6064-6070. doi: 10.7498/aps.59.6064 [13] 张小安, 杨治虎, 王党朝, 梅策香, 牛超英, 王伟, 戴斌, 肖国青. 类钴氙离子入射Ni表面激发的红外光谱线和X射线谱. , 2009, 58(10): 6920-6925. doi: 10.7498/aps.58.6920 [14] 张丽卿, 张崇宏, 杨义涛, 姚存峰, 孙友梅, 李炳生, 赵志明, 宋书建. 高电荷态离子126Xeq+引起GaN表面形貌变化研究. , 2009, 58(8): 5578-5584. doi: 10.7498/aps.58.5578 [15] 徐忠锋, 刘丽莉, 赵永涛, 陈亮, 朱键, 王瑜玉, 肖国青. 不同能量的高电荷态Ar12+离子辐照对Au纳米颗粒尺寸的影响. , 2009, 58(6): 3833-3838. doi: 10.7498/aps.58.3833 [16] 彭海波, 王铁山, 韩运成, 丁大杰, 徐 鹤, 程 锐, 赵永涛, 王瑜玉. 高电荷态离子与Si(110)晶面碰撞的沟道效应研究. , 2008, 57(4): 2161-2164. doi: 10.7498/aps.57.2161 [17] 王 立, 张小安, 杨治虎, 陈熙萌, 张红强, 崔 莹, 邵剑雄, 徐 徐. 高电荷态离子入射Al表面库仑势对靶原子特征谱线强度的影响. , 2008, 57(1): 137-142. doi: 10.7498/aps.57.137 [18] 赵永涛, 肖国青, 徐忠锋, Abdul Qayyum, 王瑜玉, 张小安, 李福利, 詹文龙. 高电荷态离子40Arq+与Si表面作用中的电子发射产额. , 2007, 56(10): 5734-5738. doi: 10.7498/aps.56.5734 [19] 孙 江, 左战春, 郭庆林, 王英龙, 怀素芳, 王 颖, 傅盘铭. 应用双光子共振非简并四波混频测量Ba原子里德伯态. , 2006, 55(1): 221-225. doi: 10.7498/aps.55.221 [20] 杨治虎, 宋张勇, 陈熙萌, 张小安, 张艳萍, 赵永涛, 崔 莹, 张红强, 徐 徐, 邵健雄, 于得洋, 蔡晓红. 高电荷态离子Arq+与不同金属靶作用产生的X射线. , 2006, 55(5): 2221-2227. doi: 10.7498/aps.55.2221
下载:
计量
- 文章访问数: 3625
- PDF下载量: 62
- 被引次数: 0
