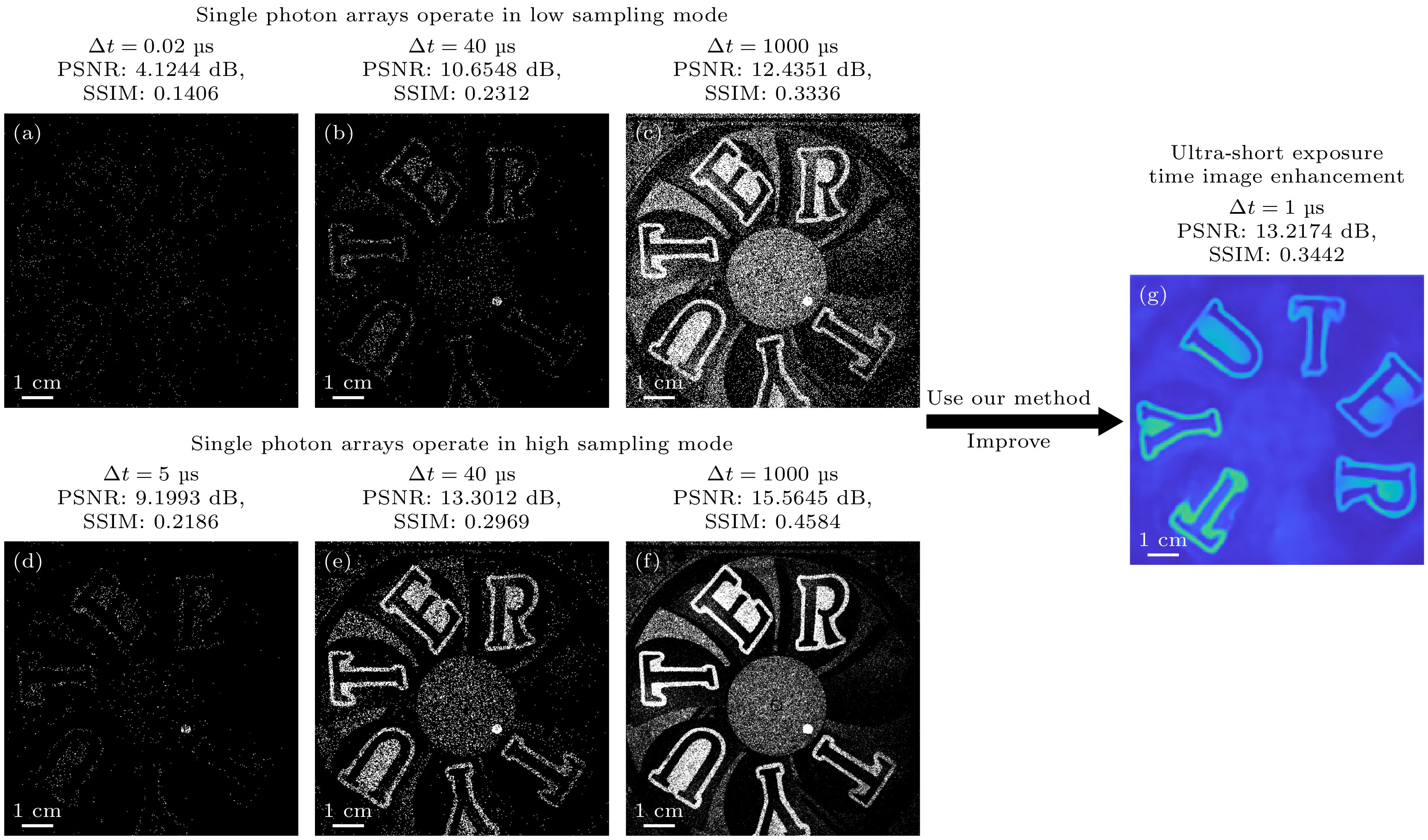
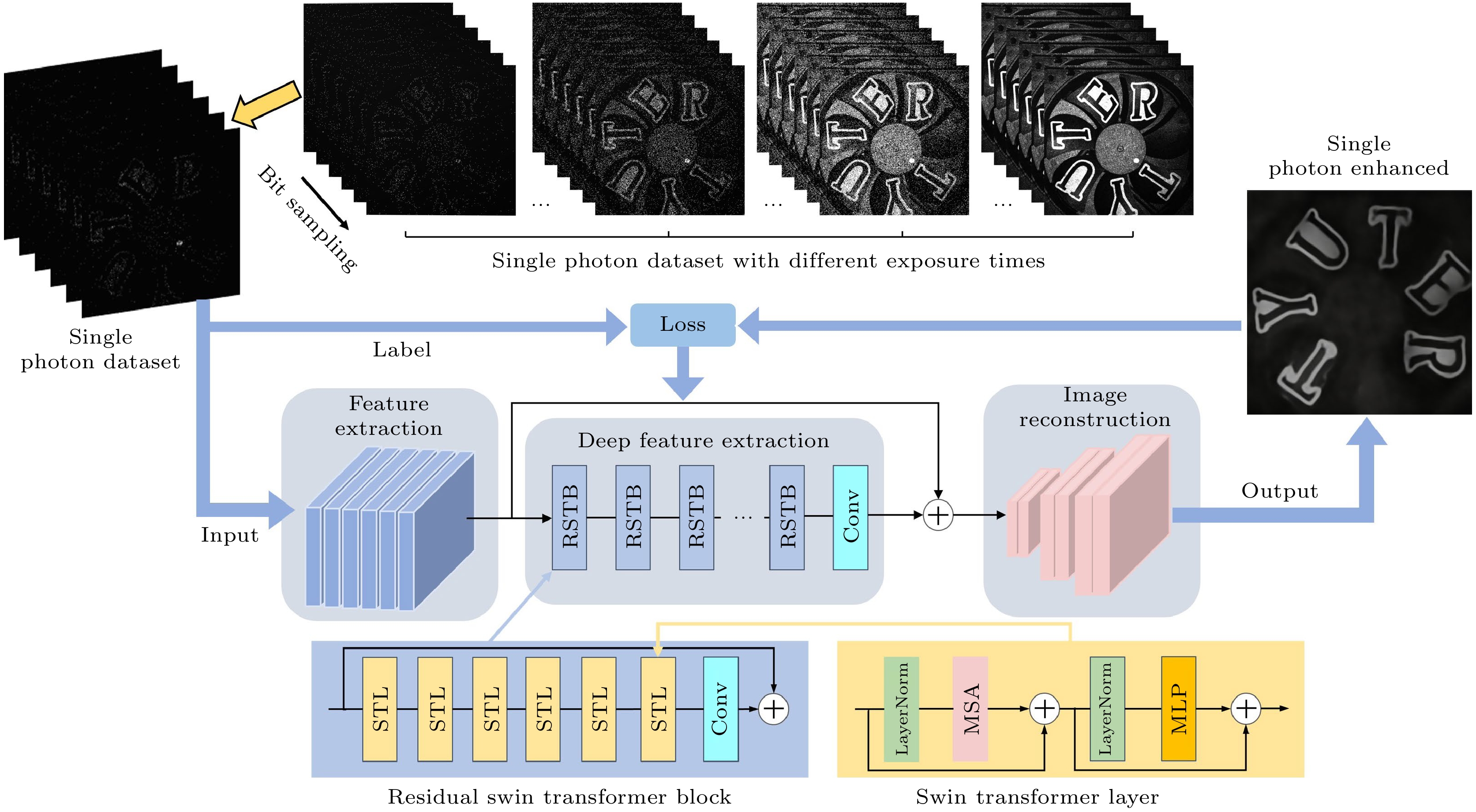
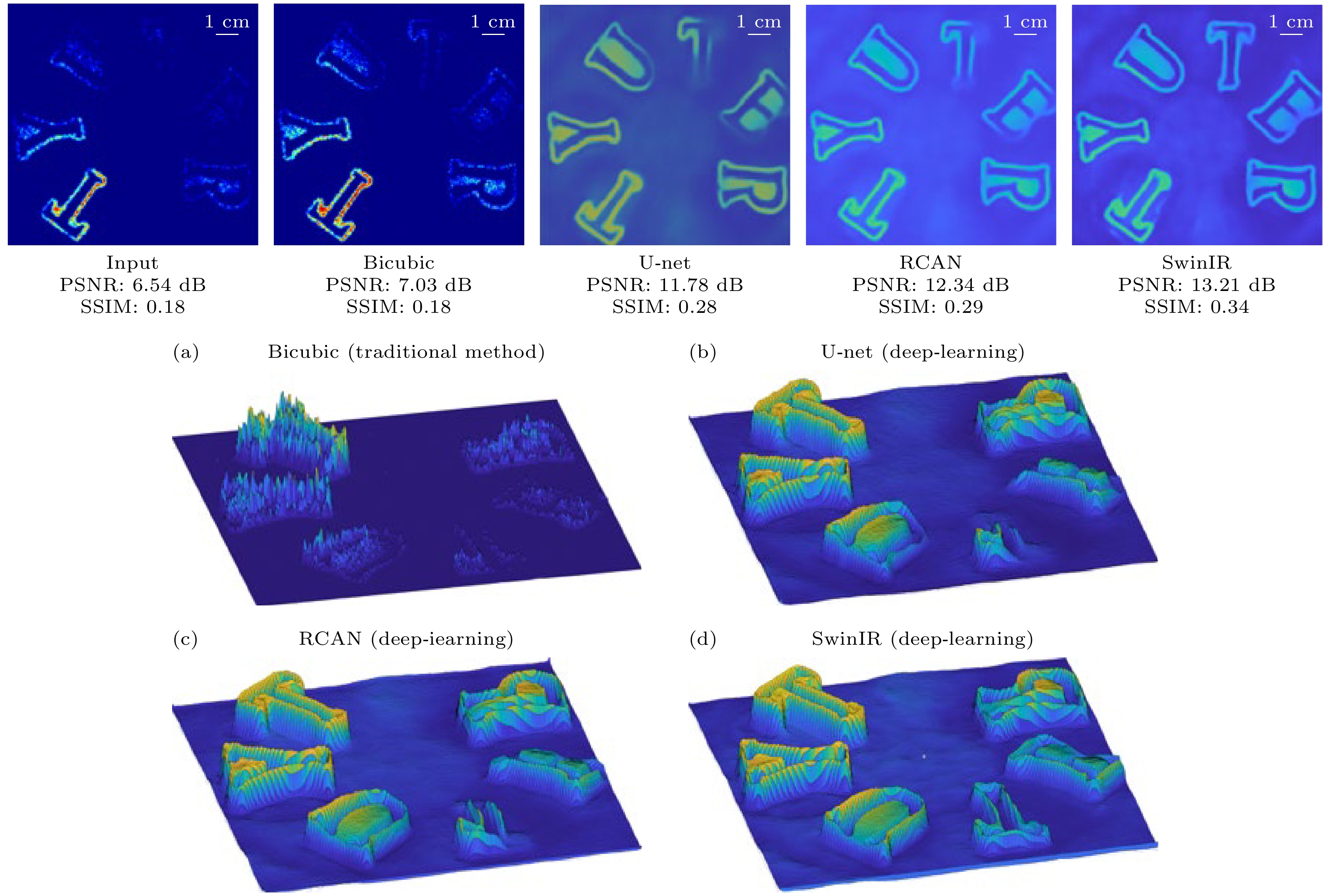
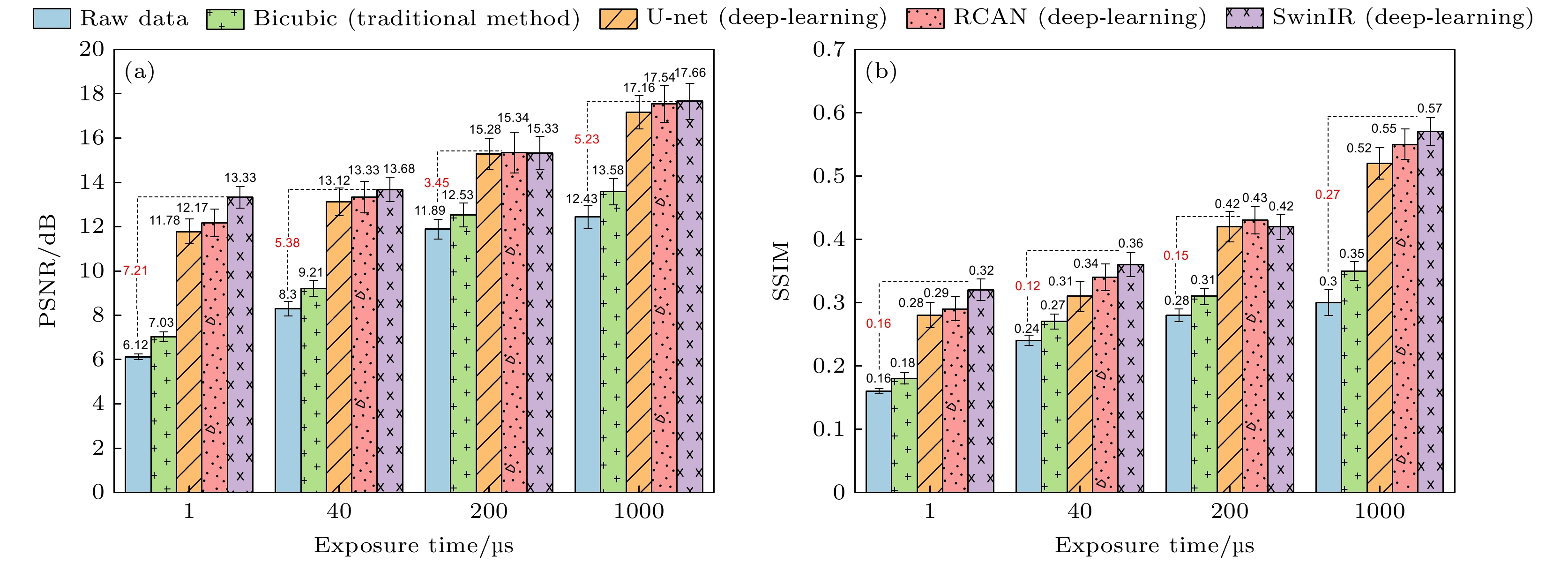
-
In recent years, with wide spread applications of high-sensitivity single-photon detectors, especially in the fields of quantum imaging and optical imaging, many important achievements have been made. and micro light imaging technology based on single-photon level has gradually become an important branch of high-resolution imaging systems. At present, the main single-photon detectors are single-photon counting avalanche diode (SPAD) sensors and support pixel arrays of different sizes, ranging from single-pixel detector sizes to tens of thousands of pixel SPAD arrays. The process structure of single-pixel SPAD detectors is relatively simple, and they are often used as the first choice for low-light imaging due to their high sensitivity, small size, and low cost. However, due to the lack of spatial resolution, single-pixel SPADs can only detect signals at a single location and cannot provide spatial information, and they are usually used in conjunction with a spatial light modulator DMD or SLM with spatial resolution to reconstruct two-dimensional (2D) images through compressed sensing or quantum correlation. Although single-pixel detectors can provide ns-level or even ps-level temporal resolution, they are limited by the frame rate of the spatial light modulator (SLM). For example, the fastest digital micromirror device (DMD) is a type of SLM with a frame rate of 22 kHz, which means that the imaging rate of a single-pixel camera is typically limited to seconds, and this camera typically uses an SPAD and an SLM for single-photon imaging tasks. This makes it a challenge to significantly improve the imaging speed, especially when higher imaging resolution is required, such as those exceeding hundreds of thousands of pixels. Assuming that the imaged object is a fast-moving dynamic target, a few seconds of imaging rate will inevitably lead to dynamic blurring, which also poses a challenge to the fast real-time performance of single-photon imaging systems. The SPAD array sensor retains the excellent sensitivity, low dark count rate, and high temporal resolution of single-pixel SPAD sensors. Due to the improvement of the fabrication process, multiple sensors and readout circuits are fabricated on the same chip, thus leading to the development of spatially resolved SPAD array camera. However, the integrated design of SPAD arrays with multiple pixels and circuits inevitably leads to cross-crosstalk between pixels. This crosstalk can significantly affect the accuracy of the signal. Additionally, the fill factor of such array cameras is typically low. Although the fill factor can be improved by methods such as three-dimensional (3D) stacking and microlens arrays, the spatial utilization is still to be improved in comparison with single-pixel SPADs. However, it is undeniable that SPAD arrays perform well in high dynamic range photon flux detection and high frame rate photon counting measurements due to the parallel processing of multiple detectors. Currently, commercial SPAD arrays integrate hundreds of thousands of detector pixel units, thereby providing excellent spatial resolution. Unfortunately, due to manufacturing processes and various challenges, the SPAD array cameras have been used in high-quantification bit deep sampling mode to acquire high-resolution single-photon intensity imaging. Its exposure time is limited to milliseconds. It is difficult to avoid dynamic blurring during the imaging exposure time when the motion frequency of the dynamic target reaches kHz or higher. Although the quantification bit depth can be sacrificed to shorten the minimum exposure time of array camera to the ns level, too short an exposure time can result in the SPAD array capturing the sparse photon data contaminated by a large amount of noise. Therefore, reliable photon denoising methods need to be developed. These methods are essential for effectively separating background noise from the actual signals, thereby improving the signal-to-noise ratio of the imaging system. Therefore, the real-time performance of the imaging system at the expense of quantification sampling accuracy still needs to be further optimized. In order to solve the problem of limited imaging quality and rate of SPAD arrays under very short exposure times, we propose a single-photon imaging enhanced deep neural network combined with super-resolution deep learning in this work. By constructing a single-photon image dataset with dynamic exposure times and conducting adaptive training, high-fidelity reconstruction of low signal-to-noise ratio single-photon images can be achieved under ultra-short exposure time. In the experiments, the enhanced reconstruction of low-quality fan images (PSNR/SSIM, 6.54 dB/0.18) under very low-light conditions is achieved, with an exposure time of only 1 μs and an average photon number of less than 0.5 photons (PNSR/SSIM, 13.21 dB/0.34). And the images are effectively improved by +7.21 dB/+0.16 for PSNR and SSIM. The passive remote enhanced reconstruction is performed on the drone at a distance of 5.19 km, with an imaging exposure time of 5 μs, and an effective PSNR and SSIM enhancement of +4.78 dB/+0.2. This method provides a new technical solution for SPAD arrays for achieving ultra-fast-exposure high-quality imaging. -
Keywords:
- single-photon counting avalanche diode array detection /
- enhanced imaging /
- deep neural network /
- ultra-fast exposure
-
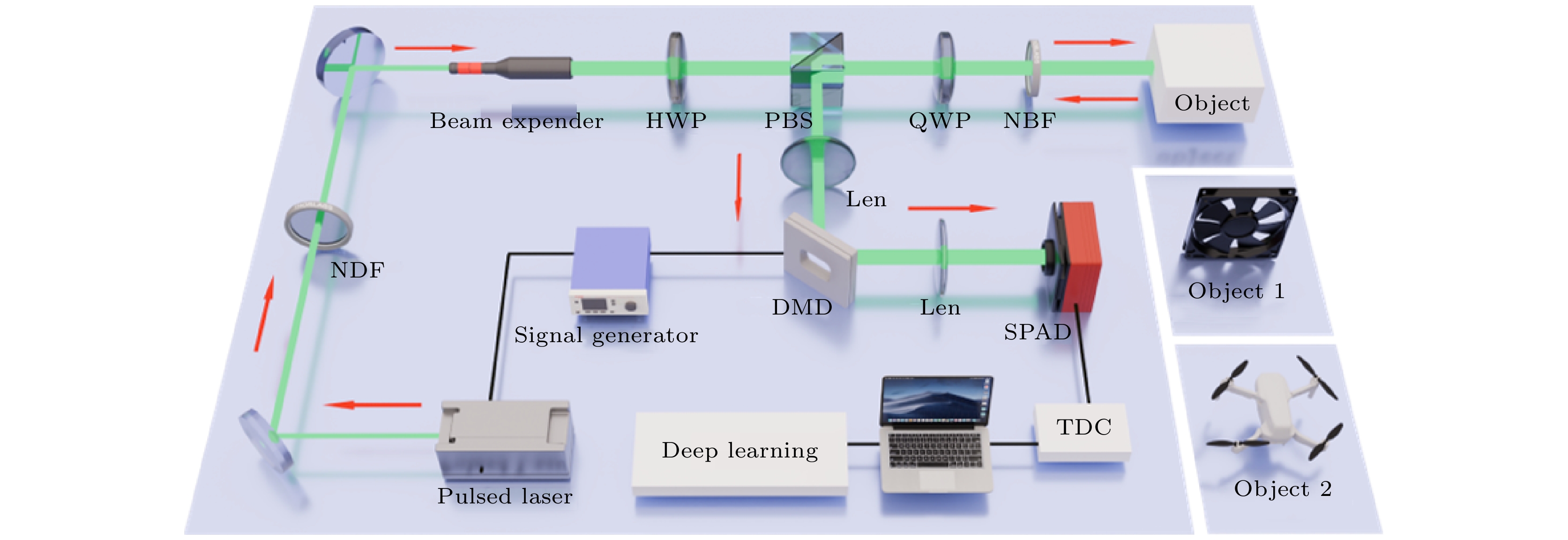
图 1 基于单光子阵列的单光子增强成像系统实验装置, 其中NDF为中性密度滤波片, DMD为数字微镜器件, HWP为半波片, PBS为偏振分束器, QWP为四分之一波片, NBF为窄带滤波片, TDC为时间数字转换器
Figure 1. Experimental measurement device for single photon enhanced imaging based on SPAD array. NDF is a neutral density filter, DMD is a digital micromirror device, HWP is a half-wave plate, PBS is a polarization beam splitter, QWP is a quarter-wave plate, NBF is a narrow-band filter, and TDC is a time-to-digital converter.
图 2 在不同采样位数条件下, 单光子阵列探测平均光子数随曝光时间变化的实验结果
Figure 2. Experimental results of the average number of photons detected by SPAD array with exposure time under different sampling bits.
图 3 单光子阵列光子数校正偏差随曝光时间的变化
Figure 3. Results of photon number correction bias with exposure time in SPAD array.
图 4 单光子阵列信噪比测试结果
Figure 4. SNR test results for SPAD array.
图 5 不同量化位深条件下, 单光子阵列实验成像的(a) PSNR和(b) SSIM随曝光时间的变化
Figure 5. The PSNR (a) and SSIM (b) of SPAD array imaging change with exposure time under different sampling bit depth.
图 6 单光子阵列超短曝光成像结果与经本文超分辨深度学习处理后的结果
Figure 6. Ultra-short exposure imaging results of SPAD array and the results processed by super-resolution deep learning.
图 7 基于SwinIR模型的单光子增强深度神经网络结构示意图
Figure 7. Schematic diagram of single-photon enhanced deep neural network architecture based on SwinIR model.
图 8 使用传统方法和3种不同深度模型的单光子增强成像重构结果
Figure 8. Results of single-photon enhanced imaging reconstruction using conventional methods and three different depth models.
图 9 传统方法和3种不同深度模型对单光子增强重构成像评价指标对比
Figure 9. Comparison of evaluation indexes between traditional methods and three different depth models in single-photon enhanced reconstruction imaging.
图 10 短曝光时间下远距离探测无人机单光子阵列增强重构成像结果
Figure 10. Enhanced imaging reconstruction results of SPAD array of long range detection UAV under short exposure time.
表 2 不同超分尺度下重构成像的详细指标对比
Table 2. Comparison of detailed indexes of reconstructed imaging at different super-resolution scales.
SPAD
exposure
time/μsSR scale Metric Bicubic U-net RCAN SwinIR 1 2 PSNR 6.79 11.42 12.34 13.11 SSIM 0.16 0.26 0.28 0.31 4 PSNR 7.03 11.78 12.17 13.33 SSIM 0.18 0.28 0.29 0.32 40 2 PSNR 10.64 12.36 13.14 13.42 SSIM 0.24 0.30 0.33 0.34 4 PSNR 11.36 13.12 13.33 13.68 SSIM 0.27 0.31 0.34 0.36 200 2 PSNR 12.11 14.23 15.02 15.31 SSIM 0.28 0.39 0.41 0.42 4 PSNR 12.53 15.28 15.34 15.33 SSIM 0.31 0.42 0.43 0.42 1000 2 PSNR 13.29 16.41 16.62 16.80 SSIM 0.32 0.44 0.46 0.48 4 PSNR 13.58 17.16 17.54 17.66 SSIM 0.35 0.52 0.55 0.57 
DownLoad: CSV
-
[1] Zia D, Dehghan N, D’Errico A, Sciarrino F, Karimi E 2023 Nat. Photonics 17 1009
Google Scholar
[2] Wang G Q, Madonini F, Li B N, Li C H, Xiang J G, Villa F, Cappellaro P 2023 Adv. Quantum Technol. 6 2300046
Google Scholar
[3] Vaidya S, Gao X, Dikshit S, Aharonovich I, Li T 2023 Adv. Phys. X 8 2206049
[4] Altmann Y, McLaughlin S, Padgett M J, Goyal V K, Hero A O, Faccio D 2018 Science 361 2298
Google Scholar
[5] 李明飞, 杨然, 霍娟, 赵连洁, 杨文良, 王俊, 张安宁 2015 64 224208
Google Scholar
Li M F, Yang R, Huo J, Zhao L J, Yang W L, Wang J, Zhang A N 2015 Acta Phys. Sin. 64 224208
Google Scholar
[6] Jiang P Y, Li Z P, Xu F 2021 Opt. Lett. 46 1181
Google Scholar
[7] Ru S Y, Hao H, Zhao Q Y, Li Z J, Liu H, Liu Z, Deng J, Huang Y H, Yang F, Liu N T, Wan C, Tu X C, Zhang L B, Jia X Q, Chen J, Kang L, Wu P H 2024 Laser Photonics Rev. 18 2400483
Google Scholar
[8] 李明飞, 阎璐, 杨然, 刘院省 2019 68 064202
Google Scholar
Li M F, Yan L, Yang R, Liu Y X 2019 Acta Phys. Sin. 68 064202
Google Scholar
[9] 李昌恒, 刘璠, 王小庆, 朱露洁, 刘雪峰 2024 光学学报 44 911002
Google Scholar
Li C H, Liu P, Wang X Q, Zhu L J, Liu X F 2024 Acta Opt. Sin. 44 911002
Google Scholar
[10] Shin D, Xu F, Venkatraman D, Lussana R, Villa F, Zappa F, Goyal V K, Wong F N C, Shapiro J H 2016 Nat. Commun. 7 12046
Google Scholar
[11] 李薇薇, 张同意, 康岩, 薛瑞凯, 王晓芳, 梁锦涛, 李力飞 2024 光子学报 53 1111001
Li W W, Zhang T Y, Kang Y, Xue R K, Wang X F, Liang J T, Li L F 2024 Acta Photonica Sin. 53 1111001
[12] Wang H, Wang X Q, Gao C, Liu X, Wang Y, Zhao H, Yao Z H 2024 Opt. Laser Technol. 170 110196
Google Scholar
[13] Li Z P, Ye J T, Huang X, Jiang P Y, Cao Y, Hong Y, Yu C, Zhang J, Zhang Q, Peng C Z, Xu F, Pan J W 2021 Optica 8 344
Google Scholar
[14] Duarte M F, Davenport M A, Takhar D, Laska J N, Sun T, Kelly K F, Baraniuk R G 2008 IEEE Signal Process. Mag. 25 83
Google Scholar
[15] Meng H Y, Gao Y, Wang X H, Li X Y, Wang L L, Zhao X, Sun B Q 2024 Light Sci. Appl. 13 121
Google Scholar
[16] Al Abbas T, Dutton N A W, Almer O, Pellegrini S, Henrion Y, Henderson R K 2016 2016 IEEE International Electron Devices Meeting IEDM San Francisco CA, USA, December 3—7, 2016 pp8.1. 1-8.1. 4
[17] Xu H, Pancheri L, Betta G F D, Stoppa D 2017 Opt. Express 25 12765
Google Scholar
[18] Tontini A, Gasparini L, Perenzoni M 2020 Sensors 20 5203
Google Scholar
[19] Ghioni M, Gulinatti A, Rech I, Zappa F, Cova S 2007 IEEE J. Sel. Top. Quant. Electron 13 852
Google Scholar
[20] Itzler M A, Ben-Michael R, Hsu C F, Slomkowski K, Tosi A, Cova S, Zappa F, Ispasoiu R 2007 J. Mod. Opt. 54 283
Google Scholar
[21] Liu F, Liu X F, Yao X R, Dou S C, Li H, Zhai G J 2022 Opt. Express 30 22608
Google Scholar
[22] Li S, Liu X Y, Xiao Y, Ma Y, Yang J, Zhu K N, Tian X 2023 Opt. Express 31 4712
Google Scholar
[23] Yang Y, Shi J H, Cao F, Peng J Y, Zeng G H 2015 Appl. Opt. 54 9277
Google Scholar
[24] Bromberg Y, Katz O, Silberberg Y 2009 Phys. Rev. A 79 053840
Google Scholar
[25] Zhang Y, Gibson G M, Edgar M P, Hammond G, Padgett M J 2020 Opt. Express 28 18180
Google Scholar
[26] Liu X Y, Ma Y, Li S, Yang J, Zhang Z Y, Tian X 2021 Opt. Express 29 37945
Google Scholar
[27] Sun M J, Edgar M P, Gibson G M, Sun B, Radwell N, Lamb R, Padgett M J 2016 Nat. Commun. 7 12010
Google Scholar
[28] 李明飞, 莫小范, 赵连洁, 霍娟, 杨然, 李凯, 张安宁 2016 65 64201
Google Scholar
Li M F, Mo X F, Zhao L J, Huo J, Yang R, Li K, Zhang A N 2016 Acta Phys. Sin. 65 64201
Google Scholar
[29] Laurenzis M 2019 Opt. Express 27 38391
Google Scholar
[30] Yao G X, Chen Y W, Jiang C, Xuan Y X, Hu X M, Liu Y, Pan Y 2022 Opt. Express 30 37323
Google Scholar
[31] Zarghami M, Gasparini L, Perenzoni M, Pancheri L 2019 Instruments 3 38
Google Scholar
[32] Ulku A C, Bruschini C, Antolović I M, Kuo Y, Ankri R, Weiss S, Michalet X, Charbon E 2019 IEEE J. Sel. Top. Quant. Electron 25 1
[33] Vargas-Sierra S, Linán-Cembrano G, Rodríguez-Vázquez Á 2015 IEEE Sens. J. 15 180
Google Scholar
[34] Morimoto K, Ardelean A, Wu M L, Ulku A C, Antolovic I M, Bruschini C, Charbon E 2020 Optica 7 346
Google Scholar
[35] Yu Zou, Bronzi D, Villa F, Weyers S 2014 2014 10th Conference on Ph. D. Research in Microelectronics and Electronics (PRIME) Grenoble, France, June 30-July 03, 2014 pp1–4
DownLoad:
Metrics
- Abstract views: 370
- PDF Downloads: 10
- Cited By: 0
