-
The precise spectra of few-electron atoms plays a pivotal role in advancing fundamental physics, including the verification of quantum electrodynamics (QED) theory, the determination of the fine-structure constants, and the exploration of nuclear properties. With the rapid development of precision measurement techniques, the demand for atomic structure data has evolved from simply confirming existence to pursuing unprecedented accuracy. To meet the growing needs for precision spectroscopy experiments, we develop a series of high-precision theoretical methods based on B-spline basis sets, such as the non-relativistic configuration interaction (B-NRCI) method, the correlated B-spline basis functions (C-BSBFs) method, and the relativistic configuration interaction (B-RCI) method. These methods use the unique properties of B-spline functions, such as locality, completeness, and numerical stability, to accurately solve the Schrödinger and Dirac equations for few-electron atoms. Our methods yield significant results, particularly for helium and helium-like ions. Using these methods, we obtain accurate energies, polarizabilities, tune-out wavelengths, and magic wavelengths. Specifically, we achieve high-precision measurements of the energy spectra of helium, providing vital theoretical support for conducting related experimental researches. Additionally, we make high-precision theoretical predictions of tune-out wavelengths, paving the way for new tests of QED theory. Furthermore, we propose effective theoretical schemes to suppress Stark shifts, thereby facilitating high-precision spectroscopy experiments of helium. The B-spline-basis methods reviewed in this paper prove exceptionally effective in high-precision calculations for few-electron atoms. These methods not only provide crucial theoretical support for precision spectroscopy experiments but also pave the new way for testing QED. Their ability to handle large-scale configuration interactions and incorporate relativistic and QED corrections makes them versatile tools for advancing atomic physics research. In the future, the high-precision theoretical methods based on B-spline basis sets are expected to be extended to cutting-edge fields, such as quantum state manipulation, determination of nuclear structure properties, formation of ultracold molecules, and exploration of new physics, thus continuously promoting the progress of precision measurement physics.
-
Keywords:
- B-spline basis sets /
- few-electron atoms /
- polarizabilities /
- Bethe-logarithm
[1] Yan Z C, Drake G W F 1995 Phys. Rev. Lett. 74 4791
Google Scholar
[2] Patkóš V, Yerokhin V A, Pachucki K 2016 Phys. Rev. A 94 052508
Google Scholar
[3] Patkóš V, Yerokhin V A, Pachucki K 2017 Phys. Rev. A 95 012508
Google Scholar
[4] Patkóš V, Yerokhin V A, Pachucki K 2019 Phys. Rev. A 100 042510
Google Scholar
[5] Patkóš V, Yerokhin V A, Pachucki K 2021 Phys. Rev. A 103 012803
Google Scholar
[6] Mitroy J, Tang L Y 2013 Phys. Rev. A 88 052515
Google Scholar
[7] Pachucki K, Yerokhin V A 2010 Phys. Rev. Lett. 104 070403
Google Scholar
[8] Beyer A, Maisenbacher L, Matveev A, Pohl R, Khabarova K, Grinin A, Lamour T, Yost D C, Hänsch T W, Kolachevsky N, Udem T 2017 Science 358 79
Google Scholar
[9] Drake G W F, Dhindsa H S, Marton V J 2021 Phys. Rev. A 104 L060801
Google Scholar
[10] Bethe H A 1947 Phys. Rev. 72 339
Google Scholar
[11] Karshenboim S G 2005 Phys. Rep. 422 1
Google Scholar
[12] Yerokhin V A, Pachucki K, Patkóš V 2019 Ann. Phys. 531 1800324
Google Scholar
[13] Drake G W F 2023 Handbook of Atomic, Molecular and Optical Physics (Cham: Springer Nature Switzerland AG 2023) pp2522–8706
[14] Pachucki K, Patkóš V, Yerokhin V A 2017 Phys. Rev. A 95 062510
Google Scholar
[15] Henson B M, Ross J A, Thomas K F, Kuhn C N, Shin D K, Hodgman S S, Zhang Y H, Tang L Y, Drake G W F, Bondy A T, Truscott A G, Baldwin K G H 2022 Science 376 199
Google Scholar
[16] James H M, Coolidge A S 1935 Phys. Rev. 47 700
[17] Mitroy J, Bubin S, Horiuchi W, Suzuki Y, Adamowicz L, Cencek W, Szalewicz K, Komasa J, Blume D, Varga K 2013 Rev. Mod. Phys. 85 693
Google Scholar
[18] McKenzie D M, Drake G W F 1991 Phys. Rev. A 44 R6973
Google Scholar
[19] Drake G W F, Yan Z C 1992 Phys. Rev. A 46 2378
Google Scholar
[20] Yan Z C, Drake G W F 1995 Phys. Rev. A 52 3711
Google Scholar
[21] Yan Z, Drake G W F 1997 J. Phys. B 30 4723
Google Scholar
[22] Tang L Y, Yan Z C, Shi T Y, Babb J F 2009 Phys. Rev. A 79 062712
Google Scholar
[23] Rooij R V, Borbely J S, Simonet J, Hoogerland M D, Eikema K S E, Rozendaal R A, Vassen W 2011 Science 333 196
Google Scholar
[24] Zheng X, Sun Y R, Chen J J, Jiang W, Pachucki K, Hu S M 2017 Phys. Rev. Lett. 118 063001
Google Scholar
[25] Kato K, Skinner T D G, Hessels E A 2018 Phys. Rev. Lett. 121 143002
Google Scholar
[26] Guan H, Chen S, Qi X Q, Liang S, Sun W, Zhou P, Huang Y, Zhang P P, Zhong Z X, Yan Z C, Drake G W F, Shi T Y, Gao K 2020 Phys. Rev. A 102 030801
Google Scholar
[27] Sun W, Zhang P P, Zhou P P, Chen S L, Zhou Z Q, Huang Y, Qi X Q, Yan Z C, Shi T Y, Drake G W F, Zhong Z X, Guan H, Gao K L 2023 Phys. Rev. Lett. 131 103002
Google Scholar
[28] Schoenberg I J 1946 Quart. Appl. Math. 4 45
Google Scholar
[29] Schoenberg I J 1967 On Spline Functions//Shisha O Inequalities (New York: Academic Press) pp255–291
[30] De Boor C 1978 A Practical Guide to Splines (New York: Springer) p157
[31] Johnson W R, Sapirstein J 1986 Phys. Rev. Lett. 57 1126
Google Scholar
[32] Johnson W R, Blundell S A, Sapirstein J 1988 Phys. Rev. A 37 307
Google Scholar
[33] Grant I P 1982 Phys. Rev. A 25 1230
Google Scholar
[34] Fischer C F 2008 Adv. At. Mol. Opt. Phys. 55 235
[35] Bachau H, Cormier E, Decleva P, Hansen J E, Martín F 2001 Rep. Prog. Phys. 64 1815
Google Scholar
[36] Xi J H, He X H, Li B W 1992 Phys. Rev. A 46 5806
Google Scholar
[37] Xi J H, Wu L J, Li B W 1993 Phys. Rev. A 47 2701
Google Scholar
[38] Rao J G, Liu W Y, Li B W 1994 Phys. Rev. A 50 1916
Google Scholar
[39] Qiao H X, Li B W 1999 Phys. Rev. A 60 3134
Google Scholar
[40] Wu L J 1996 Phys. Rev. A 53 139
Google Scholar
[41] Yu K Z, Wu L J, Gou B C, Shi T Y 2004 Phys. Rev. A 70 012506
Google Scholar
[42] Zhang Y H, Tang L Y, Zhang X Z, Jiang J, Mitroy J 2012 J. Chem. Phys. 136 174107
Google Scholar
[43] Zhang Y H, Tang L Y, Zhang X Z, Shi T Y, Mitroy J 2012 Chin. Phys. Lett. 29 063101
Google Scholar
[44] Tang L Y, Zhang Y H, Zhang X Z, Jiang J, Mitroy J 2012 Phys. Rev. A 86 012505
Google Scholar
[45] Zhang Y H, Tang L Y, Zhang X Z, Shi T Y 2015 Phys. Rev. A 92 012515
Google Scholar
[46] Zhang Y H, Tang L Y, Zhang X Z, Shi T Y 2016 Chin. Phys. B 25 103101
Google Scholar
[47] Zhang Y H, Tang L Y, Zhang X Z, Shi T Y 2016 Phys. Rev. A 93 052516
Google Scholar
[48] Wu F F, Yang S J, Zhang Y H, Zhang J Y, Qiao H X, Shi T Y, Tang L Y 2018 Phys. Rev. A 98 040501(R
Google Scholar
[49] Zhang Y H, Wu F F, Zhang P P, Tang L Y, Zhang J Y, Baldwin K G H, Shi T Y 2019 Phys. Rev. A 99 040502(R
Google Scholar
[50] Zhang Y H, Tang L Y, Shi T Y 2021 Phys. Rev. A 104 042817
Google Scholar
[51] Zhang Y H, Tang L Y, Zhang J Y, Shi T Y 2021 Phys. Rev. A 103 032810
Google Scholar
[52] Yang S J, Mei X S, Shi T Y, Qiao H X 2017 Phys. Rev. A 95 062505
Google Scholar
[53] Fang H, Zhang Y H, Zhang P P, Shi T Y 2023 Phys. Rev. A 108 062818
Google Scholar
[54] Fang H, Zhang Y H, Li Y T, Shi T Y 2024 Phys. Rev. A 110 062823
Google Scholar
[55] Yang S J, Tang Y B, Zhao Y H, Shi T Y, Qiao H X 2019 Phys. Rev. A 100 042509
Google Scholar
[56] Decleva P, Lisini A, Venuti M 1995 Int. J. Quantum Chem. 56 27
Google Scholar
[57] Chen M H, Cheng K T, Johnson W R 1993 Phys. Rev. A 47 3692
Google Scholar
[58] Wu F F, Shi T Y, Ni W T, Tang L Y 2023 Phys. Rev. A 108 L051101
Google Scholar
[59] Lamb W E, Retherford R C 1947 Phys. Rev. 72 241
Google Scholar
[60] Drake G W F, Martin W C 1998 Can. J. Phys. 76 679
[61] Goldman S P 1984 Phys. Rev. A 30 1219
Google Scholar
[62] Goldman S P, Drake G W F 2000 Can. J. Phys. 61 052513
[63] Drake G W F, Goldman S P 2000 Can. J. Phys. 77 835
Google Scholar
[64] Goldman S P 1994 Phys. Rev. A 50 3039
Google Scholar
[65] Zhang Y H, Shen L J, Xiao C M, Zhang J Y, Shi T Y 2020 J. Phys. B 53 135003
Google Scholar
[66] Jentschura U D, Mohr P J 2005 Phys. Rev. A 72 012110
Google Scholar
[67] Tang Y B, Zhong Z X, Li C B, Qiao H X, Shi T Y 2013 Phys. Rev. A 87 022510
Google Scholar
[68] Kabir P K, Salpeter E E 1957 Phys. Rev. 108 1256
Google Scholar
[69] Dalgarno A, Stewart A L 1960 Proc. Phys. Soc. A 76 49
Google Scholar
[70] Schwartz C 1961 Phys. Rev. 123 1700
Google Scholar
[71] Korobov V I, Korobov S V 1999 Phys. Rev. A 59 3394
Google Scholar
[72] Korobov V I 2012 Phys. Rev. A 85 042514
Google Scholar
[73] Korobov V I 2019 Phys. Rev. A 100 012517
Google Scholar
[74] Notermans R P M J W, Rengelink R J, van Leeuwen K A H, Vassen W 2014 Phys. Rev. A 90 052508
Google Scholar
[75] Ludlow A D, Boyd M M, Ye J, Peik E, Schmidt P O 2015 Rev. Mod. Phys. 87 637
Google Scholar
[76] Arora B, Sahoo B K 2014 Phys. Rev. A 89 022511
Google Scholar
[77] Porsev S G, Safronova M S, Derevianko A, Clark C W 2014 Phys. Rev. A 89 022703
Google Scholar
[78] Puchalski M, Piszczatowski K, Komasa J, Jeziorski B, Szalewicz K 2016 Phys. Rev. A 93 032515
Google Scholar
[79] Puchalski M, Szalewicz K, Lesiuk M, Jeziorski B 2020 Phys. Rev. A 101 022505
Google Scholar
[80] Dzuba V A, Flambaum V V, Sushkov O P 1997 Phys. Rev. A 56 R4357
Google Scholar
[81] Mitroy J, Safronova M S, Clark C W 2010 J. Phys. B 43 202001
Google Scholar
[82] Derevianko A, Savukov I M, Johnson W R, Plante D R 1998 Phys. Rev. A 58 4453
Google Scholar
[83] Johnson W, Plante D, Sapirstein J 1995 Adv. At., Mol., Opt. Phys. 35 255
[84] Pachucki K, Komasa J 2004 Phys. Rev. Lett. 92 213001
Google Scholar
[85] LeBlanc L J, Thywissen J H 2007 Phys. Rev. A 75 053612
Google Scholar
[86] Holmgren W F, Trubko R, Hromada I, Cronin A D 2012 Phys. Rev. Lett. 109 243004
Google Scholar
[87] Copenhaver E, Cassella K, Berghaus R, Müller H 2019 Phys. Rev. A 100 063603
Google Scholar
[88] Meng Z, Wang L, Han W, Liu F, Wen K, Gao C, Wang P, Chin C, Zhang J 2023 Nature 615 231
Google Scholar
[89] Henson B M, Khakimov R I, Dall R G, Baldwin K G H, Tang L Y, Truscott A G 2015 Phys. Rev. Lett. 115 043004
Google Scholar
[90] Lu S S, Zhang Y H, Shi T Y, Tang L Y 2025 J. Phys. B 58 035002
Google Scholar
[91] Katori H, Takamoto M, Pal’chikov V G, Ovsiannikov V D 2003 Phys. Rev. Lett. 91 173005
Google Scholar
[92] Takamoto M, Katori H 2003 Phys. Rev. Lett. 91 223001
Google Scholar
[93] Bothwell T, Kennedy C J, Aeppli A, Kedar D, Robinson J M, Oelker E, Staron A, Ye J 2022 Nature 602 420
Google Scholar
[94] Zheng X, Dolde J, Lochab V, Merriman B N, Li H, Kolkowitz 2022 Nature 602 425
Google Scholar
[95] McGrew W F, Zhang X, Fasano R J, Schäffer S A, Beloy K, Nicolodi D, Brown R C, Hinkley N, Milani G, Schioppo M, Yoon T H, Ludlow A D 2018 Nature 564 87
Google Scholar
[96] Rengelink R J, van der Werf Y, Notermans R P M J W, Jannin R, Eikema K S E, Hoogerland M D, Vassen W 2018 Nat. Phys. 14 1132
Google Scholar
[97] van der Werf Y, Steinebach K, Jannin R, Bethlem H L, Eikema K S E 2023 arXiv: 2306.02333v1
[98] Thomas K F, Ross J A, Henson B M, Shin D K, Baldwin K G H, Hodgman S S, Truscott A G 2020 Phys. Rev. Lett. 125 013002
Google Scholar
-
图 1 基于B-样条函数的多种高精度理论方法框架图
Figure 1. Framework diagram of various high-precision theoretical methods based on B-spline functions
图 2 在$ [0, 1000] $区间内, 10个7阶均匀分布型的B-样条函数
Figure 2. Ten 7th-order uniformly distributed B-spline functions within the interval $ [0, 1000] $
图 3 在$ [0, 1000] $区间内, 10个7阶指数分布型的B-样条函数
Figure 3. Ten 7th-order exponentially distributed B-spline functions within the interval $ [0, 1000] $
图 4 幻零波长$ \lambda_{\mathrm{t}} $和魔幻波长$ \lambda_{\mathrm{m}} $的示意图
Figure 4. Schematic diagram of tune-out wavelength $ \lambda_{\mathrm{t}} $ and magic wavelength $ \lambda_{\mathrm{m}} $
图 5 氦原子亚稳态413 nm幻零波长的位置
Figure 5. The position of the 413 nm tune-out wavelength for the metastable state of helium
图 6 氦原子413 nm幻零波长的研究历程
Figure 6. Research roadmap of the 413 nm tune-out wavelength for the metastable state of helium
图 8 氦原子$ 2\, ^3 {\mathrm{S}}_1\rightarrow 2\, ^1 {\mathrm{S}}_0 $跃迁下的魔幻波长, 其中绿色圆圈所示的位置是319.8 nm的魔幻波长
Figure 8. The magic wavelengths for the transition $ 2\, ^3 {\mathrm{S}}_1\rightarrow $$ 2\, ^1 {\mathrm{S}}_0 $ of helium, where the position indicated by the green circle corresponds to the 319.8 nm magic wavelength.
图 9 4He原子$ 2\, ^3 {\mathrm{S}}_1\rightarrow 3\, ^3 {\mathrm{S}}_1 $的双光子激发跃迁方案图
Figure 9. The two-photon excitation scheme for the $ 2\, ^3 {\mathrm{S}}_1\rightarrow $$ 3\, ^3 {\mathrm{S}}_1 $ transition of 4He.
表 1 无穷核质量下, 氦原子基态非相对论能量(原子单位)随最大分波数$ \ell_{{\mathrm{max}}}$增加的收敛性检验
Table 1. Convergence test for the non-relativistic energy (in a.u.) of ground-state helium with infinite nuclear mass, as the maximum partial wave $ \ell_{{\mathrm{max}}}$ increases.
DownLoad: CSV
表 2 加速度规范下, 氢原子基态贝特对数项$\beta(1 {\mathrm{s}})$(原子单位)随指数结点参数$\gamma_0$的变化. 其中, $t_1$为第一个非零结点, $E_{{\mathrm{max}}}$为中间态的最大能量值. 在计算过程中, 样条个数$N=300$, 样条阶数$k=15$, 盒子半径$R_0=200$个原子单位
Table 2. Values of the Bethe logarithm $\beta(1 {\mathrm{s}})$ (in a.u.) for the ground-state hydrogen in the acceleration gauge, evaluated at different knot sequences. Where $\gamma_0$ denotes the parameter of exponential knot sequences, $t_1$ represents the first interior knot point, and $E_{{\mathrm{max}}}$ indicates the highest energy. All calculations are carried out using the same set of parameters: N = 300, k = 15, and $R_0$=200 a.u.
$ \gamma_0 $ $ t_1 $ $ E_{{\mathrm{max}}} $ $ \beta(1 {\mathrm{s}}) $ 0.005 4.10×10–1 5.76×103 2.258 0.025 2.41×10–2 1.59×106 2.2890 0.035 4.59×10–3 4.32×107 2.29061 0.045 8.06×10–4 1.38×109 2.290915 0.065 2.17×10–5 1.83×1013 2.2909796 0.075 3.43×10–7 7.23×1015 2.29098109 0.085 5.32×10–7 2.96×1018 2.290981330 0.105 1.23×10–9 5.38×1020 2.2909813741 0.115 1.84×10–10 2.36×1022 2.29098137505 0.125 2.74×10–10 1.05×1023 2.29098137518 0.135 4.04×10–11 4.75×1023 2.2909813752020 0.145 5.94×10–12 2.16×1025 2.29098137520502 0.165 1.26×10–13 4.65×1028 2.290981375205541 0.175 1.83×10–14 2.17×1030 2.2909813752055506 0.185 2.65×10–15 1.03×1032 2.29098137520555206 0.195 3.82×10–16 4.86×1033 2.29098137520555227 0.205 5.49×10–17 2.32×1035 2.290981375205552296 0.225 1.13×10–18 5.35×1038 2.29098137520555230124 0.235 1.60×10–19 6.31×1039 2.2909813752055523013355
DownLoad: CSV
表 3 不同方法计算得到的氦原子$n\, ^1 {\mathrm{S}}(n= 1—7)$态贝特对数的比较. 第二列和第三列的第一项数据来自加速度规范, 而第二项数据来自速度-加速度混合规范. 括号中的数字表示计算结果的不确定度
Table 3. Comparison of Bethe logarithms for the $n\, ^1 {\mathrm{S}}(n=1-7)$ states of helium obtained from different methods. The first entries in the second and third columns are from the acceleration gauge, while the second entries are from the mixed velocity-acceleration gauge. The Numbers in parentheses represent the computational uncertainties.
State B-NRCI[65] C-BSBFs[55] Integration method[73] $ 1\, ^1 {\mathrm{S}} $ 4.37034(2) 4.37016022(5) 4.3701602230703(3) 4.37014(2) 4.3701601(1) $ 2\, ^1 {\mathrm{S}} $ 4.36643(1) 4.36641271(1) 4.366412726417(1) 4.366412(1) 4.3664127(1) $ 3\, ^1 {\mathrm{S}} $ 4.369170(1) 4.36916480(6) 4.369164860824(2) 4.3691643(2) 4.3691648(1) $ 4\, ^1 {\mathrm{S}} $ 4.369893(1) 4.36989065(5) 4.369890632356(3) 4.3698903(5) 4.3698906(1) $ 5\, ^1 {\mathrm{S }}$ 4.370152(3) 4.3701520(1) 4.370151796310(4) 4.3701511(2) 4.3701519(1) $ 6\, ^1 {\mathrm{S }}$ 4.37027(1) 4.370267(1) 4.370266974319(5) 4.370266(2) 4.370267(1) $ 7\, ^1{\mathrm{ S}} $ 4.37033(1) 4.370326(1) 4.370325261772(5) 4.37033(1) 4.370326(1)
DownLoad: CSV
表 4 氦-4原子基态静电偶极极化率(原子单位)的结果比较. “NR”表示非相对论极化率, “Rel.”表示相对论极化率, “Total”表示考虑QED修正后的最终极化率. 括号中的数字表示计算结果的不确定度
Table 4. Comparison of the static dipole polarizability $\alpha_1(0)$ (in a.u.) for the ground state of 4He. “NR” denotes the non-relativistic polarizability, “Rel.” represents the relativistic polarizability, and “Total” stands for the final polarizability including QED corrections. The numbers in parentheses indicate the computational uncertainties.
DownLoad: CSV
表 5 关联B-样条基组方法计算的氦-4原子$n\, ^1 {\mathrm{S}}_0(n=2—7)$和$n\, ^3 {\mathrm{S}}_1(n=2—7)$激发态的静电偶极极化率(原子单位). 对于$n\, ^3 {\mathrm{S}}_1$态的张量极化率, 斜杠前的数值对应于$n\, ^3 {\mathrm{P}}_{0, 1, 2}$中间态的贡献, 斜杠后的数值对应于$n\, ^3 {\mathrm{D}}_1$中间态的贡献. 括号中的数字为计算结果的不确定度
Table 5. Static dipole polarizabilities (in a.u.) calculated using the correlated B-spline basis sets for the excited $n\, ^1 {\mathrm{S}}_0(n=2-7)$ and $n\, ^3 {\mathrm{S}}_1(n=2-7)$ states of $^4$He. For the tensor polarizability of the $n\, ^3 {\mathrm{S}}_1$ states, the number before the slash corresponds to the contribution from the $n\, ^3{\mathrm{ P}}_J$ intermediate states, and the number after the slash corresponds to the contribution from the $n\, ^3 {\mathrm{D}}_1$ intermediate states. Numbers in parentheses represent computational uncertainties
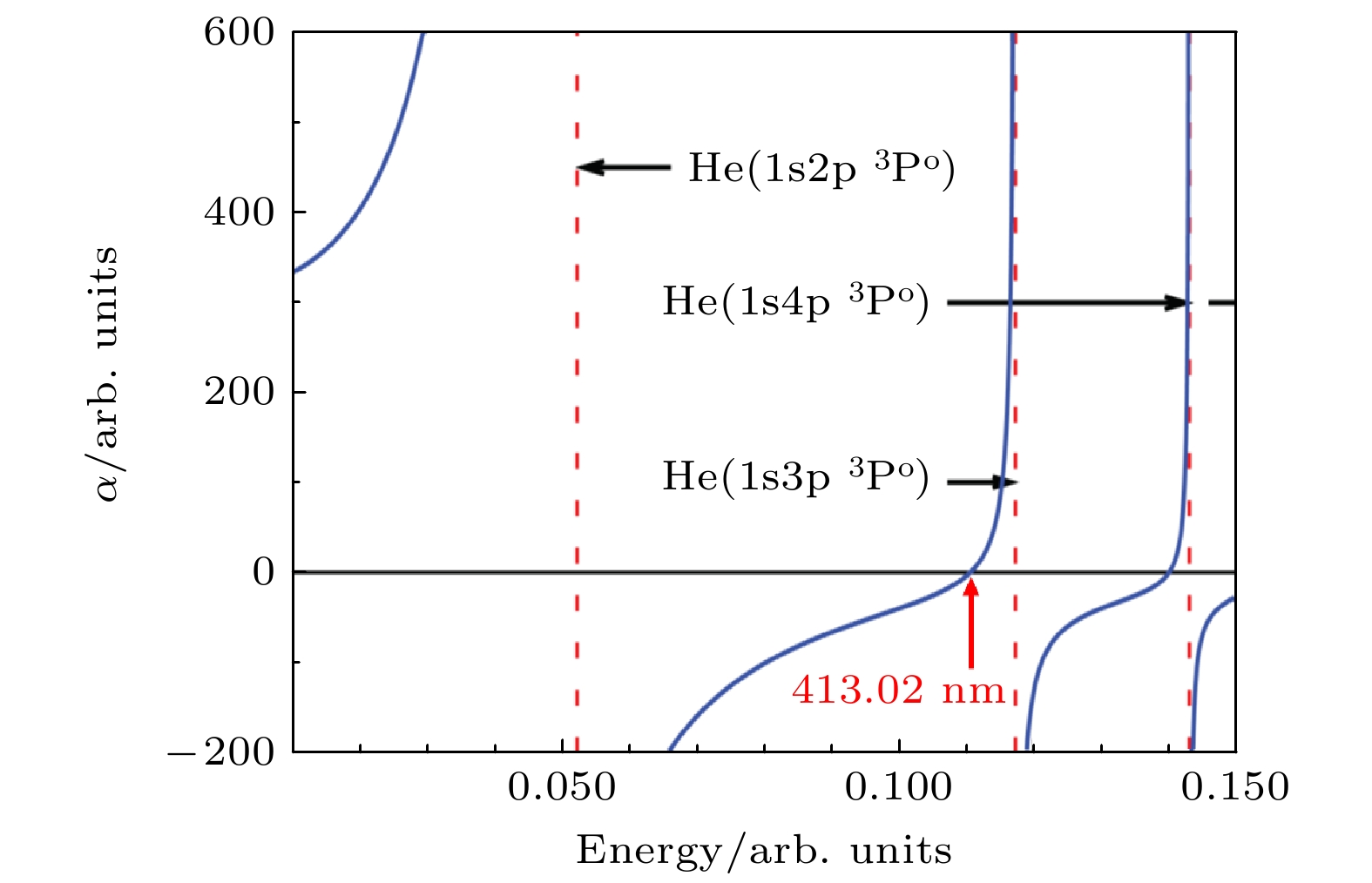
n $ \alpha_1(n\, ^1 {\mathrm{S}}_0) $ $ \alpha_1^{\mathrm{S}}(n\, ^3 {\mathrm{S}}_1) $ $ \alpha_1^{\mathrm{T}}(n\, ^3 {\mathrm{S}}_1) $ 2 800.52195(14) 315.728536(48) 0.002764488(2)/0.000726892(6) 3 16890.5275(28) 7940.5494(13) 0.09715509(3)/–0.005470(2) 4 135875.295(23) 68677.988(11) 0.9558(3)/–0.1189(2) 5 669694.55(11) 351945.328(60) 5.2676(2)/–0.7829(3) 6 2443625.15(40) 1315529.52(23) 20.654(3)/–3.291(2) 7 7269026.8(1.2) 3977532.95(69) 64.62(3)/–10.65(3)
DownLoad: CSV
表 6 在激光偏振与量子轴夹角不同的情形下, 氦原子413 nm幻零波长(纳米单位)的结果比对. 第三列代表偏振方向与量子轴平行, 且初态磁量子数$M_J=0$时的情况; 第四列代表偏振方向与量子轴平行, 且初态磁量子数为$M_J=\pm 1$时的情况; 第五列代表偏振方向与量子轴垂直, 且初态量子数$M_J=\pm 1$时的情况
Table 6. Comparison of the 413 nm tune-out wavelength (in nm) for the $2\, ^3 {\mathrm{S}}_1$ state of 4He, with varying the initial magnetic quantum number$M_J$ values, under different angles between laser polarization and the quantization axis. The third column represents the case where the polarization direction is parallel to the quantization axis and $M_J=0$. The fourth column represents the case where the polarization direction is parallel to the quantization axis but with $M_J=\pm 1$. The fifth column represents the case where the polarization direction is perpendicular to the quantization axis, with $M_J=\pm 1$.
Reference Method $ \alpha_1^{\mathrm{S}}(\omega)-2\alpha_1^{\mathrm{T}}(\omega) $ $ \alpha_1^{\mathrm{S}}(\omega)+\alpha_1^{\mathrm{T}}(\omega) $ $ \alpha_1^{\mathrm{S}}(\omega)-\tfrac{1}{2}\alpha_1^{\mathrm{T}}(\omega) $ Ref. [6] Hybrid model 413.02(9) Ref. [89] Expt. 413.0938(9stat)(20syst) Ref. [47] RCI 413.080 1(4) 413.085 9(4) Ref. [49] RCI+NRQED 413.084 26(4) 413.090 15(4) Ref. [15] Expt. 413.087 08(15) Ref. [15] NRQED 413.087 179(6) Ref. [90] RCIRP 413.084 28(5) 413.090 17(3) 413.087 23(3)
DownLoad: CSV
表 7 氦原子$2\, ^3{\mathrm{ S}}\rightarrow 2\, ^1 {\mathrm{S}}$双禁戒跃迁下319.8 nm魔幻波长理论与实验的对比
Table 7. Comparison of the 319.8 nm magic wavelength between theory and experiment for the doubly forbidden transition $2\, ^3 {\mathrm{S}}\rightarrow 2\, ^1 {\mathrm{S}}$ of helium.
DownLoad: CSV
-
[1] Yan Z C, Drake G W F 1995 Phys. Rev. Lett. 74 4791
Google Scholar
[2] Patkóš V, Yerokhin V A, Pachucki K 2016 Phys. Rev. A 94 052508
Google Scholar
[3] Patkóš V, Yerokhin V A, Pachucki K 2017 Phys. Rev. A 95 012508
Google Scholar
[4] Patkóš V, Yerokhin V A, Pachucki K 2019 Phys. Rev. A 100 042510
Google Scholar
[5] Patkóš V, Yerokhin V A, Pachucki K 2021 Phys. Rev. A 103 012803
Google Scholar
[6] Mitroy J, Tang L Y 2013 Phys. Rev. A 88 052515
Google Scholar
[7] Pachucki K, Yerokhin V A 2010 Phys. Rev. Lett. 104 070403
Google Scholar
[8] Beyer A, Maisenbacher L, Matveev A, Pohl R, Khabarova K, Grinin A, Lamour T, Yost D C, Hänsch T W, Kolachevsky N, Udem T 2017 Science 358 79
Google Scholar
[9] Drake G W F, Dhindsa H S, Marton V J 2021 Phys. Rev. A 104 L060801
Google Scholar
[10] Bethe H A 1947 Phys. Rev. 72 339
Google Scholar
[11] Karshenboim S G 2005 Phys. Rep. 422 1
Google Scholar
[12] Yerokhin V A, Pachucki K, Patkóš V 2019 Ann. Phys. 531 1800324
Google Scholar
[13] Drake G W F 2023 Handbook of Atomic, Molecular and Optical Physics (Cham: Springer Nature Switzerland AG 2023) pp2522–8706
[14] Pachucki K, Patkóš V, Yerokhin V A 2017 Phys. Rev. A 95 062510
Google Scholar
[15] Henson B M, Ross J A, Thomas K F, Kuhn C N, Shin D K, Hodgman S S, Zhang Y H, Tang L Y, Drake G W F, Bondy A T, Truscott A G, Baldwin K G H 2022 Science 376 199
Google Scholar
[16] James H M, Coolidge A S 1935 Phys. Rev. 47 700
[17] Mitroy J, Bubin S, Horiuchi W, Suzuki Y, Adamowicz L, Cencek W, Szalewicz K, Komasa J, Blume D, Varga K 2013 Rev. Mod. Phys. 85 693
Google Scholar
[18] McKenzie D M, Drake G W F 1991 Phys. Rev. A 44 R6973
Google Scholar
[19] Drake G W F, Yan Z C 1992 Phys. Rev. A 46 2378
Google Scholar
[20] Yan Z C, Drake G W F 1995 Phys. Rev. A 52 3711
Google Scholar
[21] Yan Z, Drake G W F 1997 J. Phys. B 30 4723
Google Scholar
[22] Tang L Y, Yan Z C, Shi T Y, Babb J F 2009 Phys. Rev. A 79 062712
Google Scholar
[23] Rooij R V, Borbely J S, Simonet J, Hoogerland M D, Eikema K S E, Rozendaal R A, Vassen W 2011 Science 333 196
Google Scholar
[24] Zheng X, Sun Y R, Chen J J, Jiang W, Pachucki K, Hu S M 2017 Phys. Rev. Lett. 118 063001
Google Scholar
[25] Kato K, Skinner T D G, Hessels E A 2018 Phys. Rev. Lett. 121 143002
Google Scholar
[26] Guan H, Chen S, Qi X Q, Liang S, Sun W, Zhou P, Huang Y, Zhang P P, Zhong Z X, Yan Z C, Drake G W F, Shi T Y, Gao K 2020 Phys. Rev. A 102 030801
Google Scholar
[27] Sun W, Zhang P P, Zhou P P, Chen S L, Zhou Z Q, Huang Y, Qi X Q, Yan Z C, Shi T Y, Drake G W F, Zhong Z X, Guan H, Gao K L 2023 Phys. Rev. Lett. 131 103002
Google Scholar
[28] Schoenberg I J 1946 Quart. Appl. Math. 4 45
Google Scholar
[29] Schoenberg I J 1967 On Spline Functions//Shisha O Inequalities (New York: Academic Press) pp255–291
[30] De Boor C 1978 A Practical Guide to Splines (New York: Springer) p157
[31] Johnson W R, Sapirstein J 1986 Phys. Rev. Lett. 57 1126
Google Scholar
[32] Johnson W R, Blundell S A, Sapirstein J 1988 Phys. Rev. A 37 307
Google Scholar
[33] Grant I P 1982 Phys. Rev. A 25 1230
Google Scholar
[34] Fischer C F 2008 Adv. At. Mol. Opt. Phys. 55 235
[35] Bachau H, Cormier E, Decleva P, Hansen J E, Martín F 2001 Rep. Prog. Phys. 64 1815
Google Scholar
[36] Xi J H, He X H, Li B W 1992 Phys. Rev. A 46 5806
Google Scholar
[37] Xi J H, Wu L J, Li B W 1993 Phys. Rev. A 47 2701
Google Scholar
[38] Rao J G, Liu W Y, Li B W 1994 Phys. Rev. A 50 1916
Google Scholar
[39] Qiao H X, Li B W 1999 Phys. Rev. A 60 3134
Google Scholar
[40] Wu L J 1996 Phys. Rev. A 53 139
Google Scholar
[41] Yu K Z, Wu L J, Gou B C, Shi T Y 2004 Phys. Rev. A 70 012506
Google Scholar
[42] Zhang Y H, Tang L Y, Zhang X Z, Jiang J, Mitroy J 2012 J. Chem. Phys. 136 174107
Google Scholar
[43] Zhang Y H, Tang L Y, Zhang X Z, Shi T Y, Mitroy J 2012 Chin. Phys. Lett. 29 063101
Google Scholar
[44] Tang L Y, Zhang Y H, Zhang X Z, Jiang J, Mitroy J 2012 Phys. Rev. A 86 012505
Google Scholar
[45] Zhang Y H, Tang L Y, Zhang X Z, Shi T Y 2015 Phys. Rev. A 92 012515
Google Scholar
[46] Zhang Y H, Tang L Y, Zhang X Z, Shi T Y 2016 Chin. Phys. B 25 103101
Google Scholar
[47] Zhang Y H, Tang L Y, Zhang X Z, Shi T Y 2016 Phys. Rev. A 93 052516
Google Scholar
[48] Wu F F, Yang S J, Zhang Y H, Zhang J Y, Qiao H X, Shi T Y, Tang L Y 2018 Phys. Rev. A 98 040501(R
Google Scholar
[49] Zhang Y H, Wu F F, Zhang P P, Tang L Y, Zhang J Y, Baldwin K G H, Shi T Y 2019 Phys. Rev. A 99 040502(R
Google Scholar
[50] Zhang Y H, Tang L Y, Shi T Y 2021 Phys. Rev. A 104 042817
Google Scholar
[51] Zhang Y H, Tang L Y, Zhang J Y, Shi T Y 2021 Phys. Rev. A 103 032810
Google Scholar
[52] Yang S J, Mei X S, Shi T Y, Qiao H X 2017 Phys. Rev. A 95 062505
Google Scholar
[53] Fang H, Zhang Y H, Zhang P P, Shi T Y 2023 Phys. Rev. A 108 062818
Google Scholar
[54] Fang H, Zhang Y H, Li Y T, Shi T Y 2024 Phys. Rev. A 110 062823
Google Scholar
[55] Yang S J, Tang Y B, Zhao Y H, Shi T Y, Qiao H X 2019 Phys. Rev. A 100 042509
Google Scholar
[56] Decleva P, Lisini A, Venuti M 1995 Int. J. Quantum Chem. 56 27
Google Scholar
[57] Chen M H, Cheng K T, Johnson W R 1993 Phys. Rev. A 47 3692
Google Scholar
[58] Wu F F, Shi T Y, Ni W T, Tang L Y 2023 Phys. Rev. A 108 L051101
Google Scholar
[59] Lamb W E, Retherford R C 1947 Phys. Rev. 72 241
Google Scholar
[60] Drake G W F, Martin W C 1998 Can. J. Phys. 76 679
[61] Goldman S P 1984 Phys. Rev. A 30 1219
Google Scholar
[62] Goldman S P, Drake G W F 2000 Can. J. Phys. 61 052513
[63] Drake G W F, Goldman S P 2000 Can. J. Phys. 77 835
Google Scholar
[64] Goldman S P 1994 Phys. Rev. A 50 3039
Google Scholar
[65] Zhang Y H, Shen L J, Xiao C M, Zhang J Y, Shi T Y 2020 J. Phys. B 53 135003
Google Scholar
[66] Jentschura U D, Mohr P J 2005 Phys. Rev. A 72 012110
Google Scholar
[67] Tang Y B, Zhong Z X, Li C B, Qiao H X, Shi T Y 2013 Phys. Rev. A 87 022510
Google Scholar
[68] Kabir P K, Salpeter E E 1957 Phys. Rev. 108 1256
Google Scholar
[69] Dalgarno A, Stewart A L 1960 Proc. Phys. Soc. A 76 49
Google Scholar
[70] Schwartz C 1961 Phys. Rev. 123 1700
Google Scholar
[71] Korobov V I, Korobov S V 1999 Phys. Rev. A 59 3394
Google Scholar
[72] Korobov V I 2012 Phys. Rev. A 85 042514
Google Scholar
[73] Korobov V I 2019 Phys. Rev. A 100 012517
Google Scholar
[74] Notermans R P M J W, Rengelink R J, van Leeuwen K A H, Vassen W 2014 Phys. Rev. A 90 052508
Google Scholar
[75] Ludlow A D, Boyd M M, Ye J, Peik E, Schmidt P O 2015 Rev. Mod. Phys. 87 637
Google Scholar
[76] Arora B, Sahoo B K 2014 Phys. Rev. A 89 022511
Google Scholar
[77] Porsev S G, Safronova M S, Derevianko A, Clark C W 2014 Phys. Rev. A 89 022703
Google Scholar
[78] Puchalski M, Piszczatowski K, Komasa J, Jeziorski B, Szalewicz K 2016 Phys. Rev. A 93 032515
Google Scholar
[79] Puchalski M, Szalewicz K, Lesiuk M, Jeziorski B 2020 Phys. Rev. A 101 022505
Google Scholar
[80] Dzuba V A, Flambaum V V, Sushkov O P 1997 Phys. Rev. A 56 R4357
Google Scholar
[81] Mitroy J, Safronova M S, Clark C W 2010 J. Phys. B 43 202001
Google Scholar
[82] Derevianko A, Savukov I M, Johnson W R, Plante D R 1998 Phys. Rev. A 58 4453
Google Scholar
[83] Johnson W, Plante D, Sapirstein J 1995 Adv. At., Mol., Opt. Phys. 35 255
[84] Pachucki K, Komasa J 2004 Phys. Rev. Lett. 92 213001
Google Scholar
[85] LeBlanc L J, Thywissen J H 2007 Phys. Rev. A 75 053612
Google Scholar
[86] Holmgren W F, Trubko R, Hromada I, Cronin A D 2012 Phys. Rev. Lett. 109 243004
Google Scholar
[87] Copenhaver E, Cassella K, Berghaus R, Müller H 2019 Phys. Rev. A 100 063603
Google Scholar
[88] Meng Z, Wang L, Han W, Liu F, Wen K, Gao C, Wang P, Chin C, Zhang J 2023 Nature 615 231
Google Scholar
[89] Henson B M, Khakimov R I, Dall R G, Baldwin K G H, Tang L Y, Truscott A G 2015 Phys. Rev. Lett. 115 043004
Google Scholar
[90] Lu S S, Zhang Y H, Shi T Y, Tang L Y 2025 J. Phys. B 58 035002
Google Scholar
[91] Katori H, Takamoto M, Pal’chikov V G, Ovsiannikov V D 2003 Phys. Rev. Lett. 91 173005
Google Scholar
[92] Takamoto M, Katori H 2003 Phys. Rev. Lett. 91 223001
Google Scholar
[93] Bothwell T, Kennedy C J, Aeppli A, Kedar D, Robinson J M, Oelker E, Staron A, Ye J 2022 Nature 602 420
Google Scholar
[94] Zheng X, Dolde J, Lochab V, Merriman B N, Li H, Kolkowitz 2022 Nature 602 425
Google Scholar
[95] McGrew W F, Zhang X, Fasano R J, Schäffer S A, Beloy K, Nicolodi D, Brown R C, Hinkley N, Milani G, Schioppo M, Yoon T H, Ludlow A D 2018 Nature 564 87
Google Scholar
[96] Rengelink R J, van der Werf Y, Notermans R P M J W, Jannin R, Eikema K S E, Hoogerland M D, Vassen W 2018 Nat. Phys. 14 1132
Google Scholar
[97] van der Werf Y, Steinebach K, Jannin R, Bethlem H L, Eikema K S E 2023 arXiv: 2306.02333v1
[98] Thomas K F, Ross J A, Henson B M, Shin D K, Baldwin K G H, Hodgman S S, Truscott A G 2020 Phys. Rev. Lett. 125 013002
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 404
- PDF Downloads: 12
- Cited By: 0
