-
In quantum optical experiments, the polarizabilities of atomic systems play a very important role, which can be used to describe the interactions of atomic systems with external electromagnetic fields. When subjected to a specific electric field such as a laser field with a particular frequency, the frequency-dependent electric-dipole (E1) dynamic polarizability of an atomic state can reach zero. The wavelength corresponding to such a frequency is referred to as the “turn-out” wavelength. In this work, the “turn-out” wavelengths for the 3s2 1S0 and 3s3p 3P0 clock states of Al+ are calculated by using the configuration interaction plus many-body perturbation theory (CI+MBPT) method. The values of energy and E1 reduced matrix elements of low-lying states of Al+ are calculated. By combining these E1 reduced matrix elements with the experimental energy values, the E1 dynamic polarizabilities of the 3s2 1S0 and 3s3p 3P0 clock states are determined in the angular frequency range of (0, 0.42 a.u.). The “turn-out” wavelengths are found at the zero-crossing points of the frequency-dependent dynamic polarizability curves for both the 3s2 1S0 and 3s3p 3P0 states. For the ground state 3s2 1S0, a single “turn-out” wavelength at 266.994(1) nm is observed. On the other hand, the excited state 3s3p 3P0 exhibits four distinct “turn-out” wavelengths, namely 184.56(1) nm, 174.433(1) nm, 121.52(2) nm, and 119.71(2) nm. The contributions of individual resonant transitions to the dynamic polarizabilities at the “turn-out” wavelengths are examined. It is observed that the resonant lines situated near a certain “turn-out” wavelength can provide dominant contributions to the polarizability, while the remaining resonant lines generally contribute minimally. When analyzing these data, we recommend accurately measuring these “turn-out” wavelengths to accurately determine the oscillator strengths or reduced matrix elements of the relevant transitions. This is crucial for minimizing the uncertainty of the blackbody radiation (BBR) frequency shift in Al+ optical clock and suppressing the systematic uncertainty. Meanwhile, precisely measuring these “turn-out” wavelengths is also helpful for further exploring the atomic structure of Al+.
-
Keywords:
- Al+ /
- polarizability /
- “tune-out” wavelengths /
- CI+MBPT
[1] Chaudhuri R K, Das B P, Freed K F 1998 J. Chem. Phys. 108 2556
Google Scholar
[2] Dong H, Jiang J, Wu Z W, Dong C Z, Gaigalas G 2021 Chin. Phys. B 30 043103
Google Scholar
[3] Zhang T X, Li J G, Liu J P 2018 Acta Phys. Sin. 67 053101 (in Chinese ) [张婷贤, 李冀光, 刘建鹏 2018 67 053101]
Google Scholar
Zhang T X, Li J G, Liu J P 2018 Acta Phys. Sin. 67 053101 (in Chinese )
Google Scholar
[4] Brewer S M, Chen J S, Hankin A M, Clements E R, Chou C W, Wineland D J, Hume D B, Leibrandt D R 2019 Phys. Rev. Lett. 123 033201
Google Scholar
[5] Cui K F, Chao S J, Sun C L, et al. 2022 Eur. Phys. J. D 76 140
Google Scholar
[6] Keller J, Burgermeister T, Kalincev D, et al. 2019 Phys. Rev. A 99 013405
Google Scholar
[7] Mitroy J, Safronova M S, Clark C W 2010 J. Phys. B: At. Mol. Opt. Phys. 43 202001
Google Scholar
[8] Kar S, Wang Y S, Wang Y, Ho Y K 2018 Can. J. Phys. 96 633
Google Scholar
[9] Cheng Y J, Jiang J, Mitroy J 2013 Phys. Rev. A 88 022511
Google Scholar
[10] Jiang J, Tang L Y, Mitroy J 2013 Phys. Rev. A 87 032518
Google Scholar
[11] Yu W W, Yu R M, Cheng Y J 2015 Chin. Phys. Lett. 32 123102
Google Scholar
[12] Yu W W, Yu R M, Cheng Y J, Zhou Y J 2016 Chin. Phys. B 25 023101
Google Scholar
[13] Safronova M S, Zuhrianda Z, Safronova U I, Clark C W 2015 Phys. Rev. A 92 040501(R
Google Scholar
[14] Holmgren W F, Trubko R, Hromada I, Cronin A D 2012 Phys. Rev. lett. 109 243004
Google Scholar
[15] Herold C D, Vaidya V D, Li X, Rolston S L, Porto J V, Safronova M S 2012 Phys. Rev. Lett. 109 243003
Google Scholar
[16] Reader J, Acquista N, Sansonetti C J, Sansonetti J E 1990 Astrophys. J. Suppl. Ser. 72 831
Google Scholar
[17] Samain D 1995 Astron. Astrophys. Suppl. Ser. 113 237
[18] Morton D C 1991 Astrophys. J. Suppl. Ser. 77 119
Google Scholar
[19] Safronova M S, Kozlov M G, Clark C W 2011 Phys. Rev. Lett. 107 143006
Google Scholar
[20] Tang Z M, Yu Y M, Jiang J, Dong C Z 2018 J. Phys. B: At. Mol. Opt. Phys. 51 125002
Google Scholar
[21] Wu L, Wang Xia, Wang T, Jiang J, Dong C Z 2023 New J. Phys. 25 043011
Google Scholar
[22] Dzuba V A, Flambaum V V, Kozlov M G 1996 Phys. Rev. A 54 3948
Google Scholar
[23] Kozlov M G, Porsev S G, Safronova M S, Tupitsyn I I 2015 Comput. Phys. Commun. 195 199
Google Scholar
[24] Tang Z M, Yu Y M, Dong C Z 2018 Chin. Phys. B 27 063101
Google Scholar
[25] Kramida A, Ralchenko Yu, Reader J, NIST ASD Team 2020 NIST Atomic Spectra Database (ver. 5.8) [Online]. Available: https://physics.nist.gov/asd. National Institute of Standards and Technology, Gaithersburg, MD
[26] Kumar R, Chattopadhyay S, Angom D, Mani B K 2021 Phys. Rev. A 103 022801
Google Scholar
[27] Mitroy J, Zhang J Y, Bromley M W J, Rollin R G 2009 Eur. Phys. J. D 53 15
Google Scholar
[28] Johnson W R, Safronova M S, Safronova U I 1997 Phys. Scr. 56 252
Google Scholar
[29] Stanek M, Glowacki L, Migdalek J 1996 J. Phys. B: At. Mol. Opt. Phys. 29 2985
Google Scholar
[30] Das B P, Idrees M 1990 Phys. Rev. A 42 6900
Google Scholar
[31] Fischer C F 2009 Phys. Scr. T134 014019
Google Scholar
[32] Ekman J, Godefroid M R, Hartman H 2014 Atoms 2 215
Google Scholar
-
图 1 3s2 1S0态和3s3p 3P0态的静态极化率随态求和计算中所考虑激发态最高主量子数n的收敛趋势
Figure 1. Trend of change of the static polarizabilities for the 3s2 1S0 and 3s3p 3P0 states with the respect to the highest principle quantum number n of the excited states included in the sum-over-states calculations.
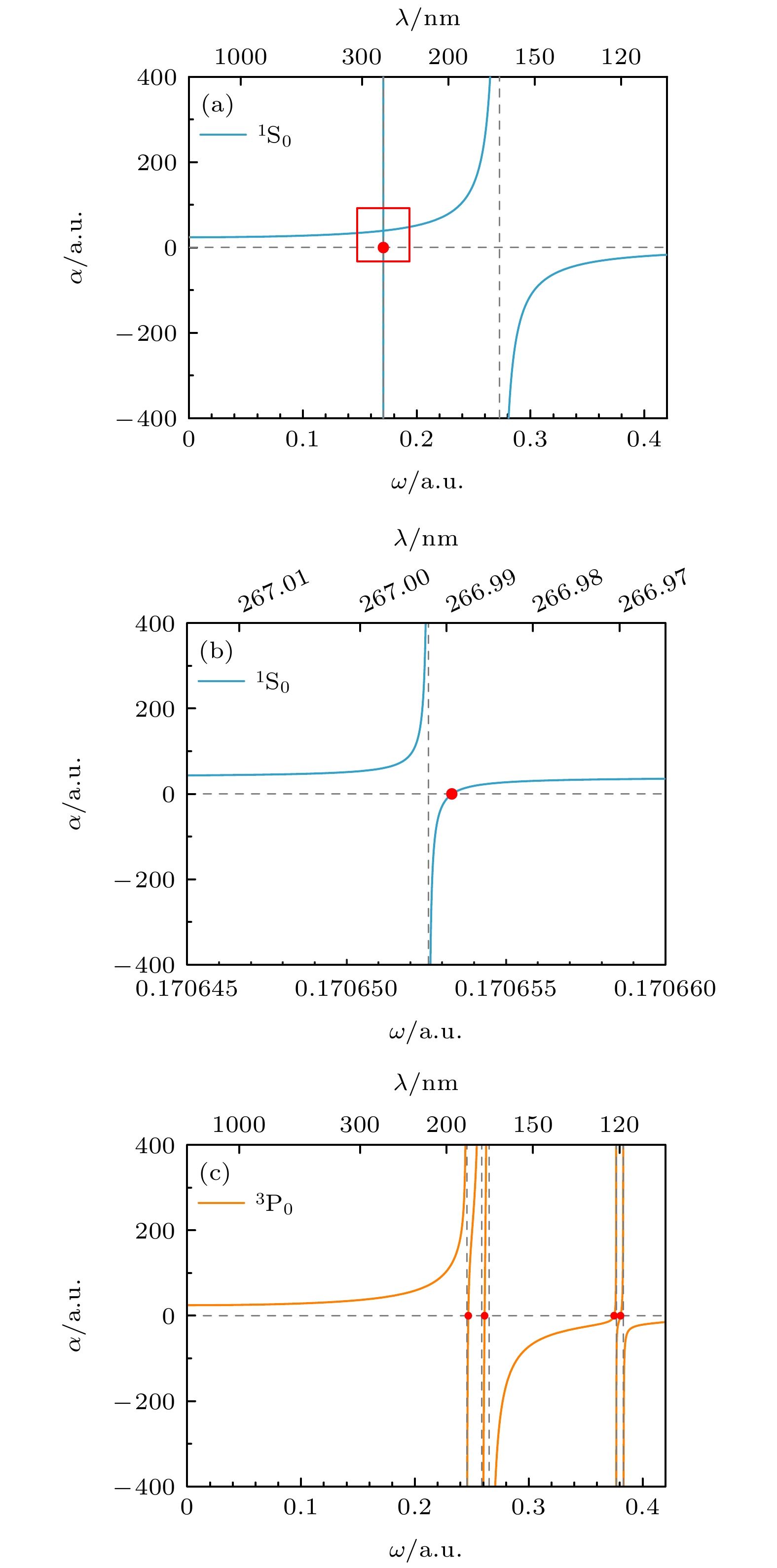
图 2 Al+的光钟态的动力学极化率 (a) 3s2 1S0态的动力学极化率; (b) 3s2 1S0态在波长267.02—266.98 nm范围内的动力学极化率; (c) 3s3p 3P0态的动力学极化率
Figure 2. Dynamic polarizabilities α(ω) of the clock states in Al+: (a) Dynamic polarizabilities α(ω) of the 3s2 1S0 state in Al+; (b) dynamic polarizabilities α(ω) of the 3s2 1S0 state in Al+ in the wavelength range between 267.02−266.98 nm; (c) dynamic polarizabilities α(ω) of the 3s3p 3P0 state in Al+.
表 1 Al+基态和激发态能级的能量值(单位: cm–1), Diff.是CI+MBPT+Breit得到的值与NIST值的相对偏差
Table 1. Energies of 27 low-lying energy levels of Al+ (in cm–1), Diff. represents the relative deviation between the value obtained from CI+MBPT+Breit and the NIST value.
State CI CI+MBPT +Breit NIST Diff./% Refs. 3s2 1S0 376617 381043 380973 381308 –0.088 381332 [19], 379582 [26], 381287 [27], 382024 [28] 3s3p 3P0 36256 37342 37344 37393.03 –0.13 37396 [19], 37395 [26], 37374 [27], 37191 [28] 3s3p 3P1 36318 37407 37405 37453.91 –0.13 37457 [19], 37452 [26], 37457 [28], 36705 [29] 3p2 1P1 59538 59905 59893 59852.02 0.069 59768 [19], 60111 [26], 60723 [27], 54410 [28], 63000 [30] 3s4s 3S1 90008 91254 91233 91274.50 –0.045 91279 [19], 91043 [26], 91262 [27], 91274 [28] 3p2 3P1 92660 94107 94097 94147.46 –0.053 94151 [19], 93380 [26], 93735 [28] 3s3d 3D1 94171 95490 95462 95551.44 –0.093 95527 [19], 95253 [26], 95695 [28] 3s4p 3P1 103975 105387 105366 105441.50 –0.071 3s4p 1P1 105574 106880 106858 106920.56 –0.058 3p2 1S0 110488 111779 111779 111637.33 0.11 3s5s 3S1 118590 120047 120022 120092.919 –0.059 3s4d 3D1 119971 121422 121395 121484.252 –0.073 3s5p 3P1 124142 125648 125624 125708.828 –0.068 3s5p 1P1 124322 125814 125790 125869.015 –0.063 3s6s 3S1 130638 132160 132134 132215.52 –0.061 3s5d 3D1 131247 132761 132734 132822.95 –0.067 3s6p 1P1 133307 134861 134835 134919.40 –0.062 3s6p 3P1 133409 134954 134928 135015.70 –0.065 3s6d 3D1 137210 138754 138727 138814.87 –0.064 3s7p 1P1 138244 139828 139802 139918.98 –0.084 3s7p 3P1 138422 139987 139960 140091.9 –0.094 3s8p 1P1 140927 142519 142493 142961.20 –0.33 3s8p 3P1 141127 142711 142685 143166.76 0.34 3s7d 3D1 140741 142300 142274 142365.54 –0.065 3s9p 1P1 143591 145260 145233 144941.10 0.20 3s9s 3S1 142835 144377 144350 144644.14 –0.20 3s8d 3D1 143118 144686 144658 144642.0 0.012 
DownLoad: CSV
表 2 使用CI+MBPT方法得到的Al+光钟态3s2 1S0和3s3p 3P0的电偶极跃迁约化矩阵元(单位: a.u.)
Table 2. Reduced matrix elements of the E1 transitions for the 3s2 1S0 and 3s3p 3P0 clock states of Al+, obtained by using the CI+MBPT method (in a.u.).
Method CI CI+MBPT Recommend Refs. Gauge Length Velocity Length Velocity 3s2 1S0-3s3p 3P1 0.0092 0.0101 0.0098 0.0105 0.0098(13) 0.01513 [26] 3s2 1S0-3s3p 1P1 3.1830 3.1572 3.1156 3.1156 3.116(67) 3.112 [19]
2.840 [26]3s2 1S0-3s4p 3P1 0.0018 0.0017 0.0022 0.0018 0.002(1) — 3s2 1S0-3s4p 1P1 0.0844 0.0781 0.0460 0.0737 0.046(38) 0.045 [19] 3s2 1S0-3s5p 3P1 0.0037 0.0038 0.0051 0.0043 0.005(2) — 3s2 1S0-3s5p 1P1 0.0474 0.0502 0.0662 0.0491 0.066(19) — 3s2 1S0-3s6p 1P1 0.0595 0.0610 0.0704 0.0586 0.070(12) — 3s2 1S0-3s6p 3P1 0.0013 0.0014 0.0023 0.0017 0.002(1) — 3s2 1S0-3s7p 1P1 0.0575 0.0582 0.0638 0.0551 0.064(9) — 3s2 1S0-3s7p 3P1 0.0015 0.0015 0.0022 0.0019 0.002(1) — 3s2 1S0-3s8p 1P1 0.0493 0.0496 0.0505 0.0448 0.051(6) — 3s2 1S0-3s8p 3P1 0.0199 0.0200 0.0250 0.0220 0.025(5) — 3s2 1S0-3s9p 1P1 0.0759 0.0758 0.0784 0.0718 0.078(7) — 3s3p 3P0-3s4s 3S1 0.8936 0.8888 0.8979 0.8926 0.898(10) 0.900 [19] 3s3p 3P0-3p2 3P1 1.8870 1.8737 1.8394 1.8789 1.839(48) 1.836 [19] 3s3p 3P0-3s3d 3D1 2.2623 2.2820 2.2350 2.2626 2.235(47) 2.236 [19] 3s3p 3P0-3s5s 3S1 0.2671 0.2652 0.2690 0.2661 0.269(4) — 3s3p 3P0-3s4d 3D1 0.4651 0.4746 0.4456 0.4612 0.446(28) — 3s3p 3P0-3s6s 3S1 0.1492 0.1481 0.1505 0.1486 0.151(2) — 3s3p 3P0-3s5d 3D1 0.2058 0.2118 0.1921 0.2029 0.192(20) — 3s3p 3P0-3s7s 3S1 0.0421 0.0418 0.0414 0.0422 0.041(1) — 3s3p 3P0-3s6d 3D1 0.1199 0.1242 0.1097 0.1178 0.110(13) — 3s3p 3P0-3s8s 3S1 0.1012 0.1004 0.1027 0.1005 0.103(2) — 3s3p 3P0-3s7d 3D1 0.0802 0.0836 0.0722 0.0787 0.072(12) — 3s3p 3P0-3s9s 3S1 0.0990 0.0983 0.0991 0.0986 0.099(1) — 3s3p 3P0-3s8d 3D1 0.0642 0.0673 0.0571 0.0630 0.057(10) —
DownLoad: CSV
表 3 相关跃迁对两个光钟态3s2 1S0和3s3p 3P0的静态极化率α(0)的贡献
Table 3. Contributions of individual transitions to the static polarizabilities α(0) for 3s2 1S0 and 3s3p 3P0.
Transition Contributions Ref. $ \alpha \left(0\right)( $3s2 1S0$ ) $ 3s2 1S0-3s3p 3P1 0.003 — 3s2 1S0-3s3p 1P1 23.73 23.661 [19]
23.7294 [27]3s2 1S0-3s4p 3P1 6.5×10–6 — 3s2 1S0-3s4p 1P1 0.0029 0.003 [19] 3s2 1S0-3s5p 3P1 3.0×10–5 — 3s2 1S0-3s5p 1P1 0.0051 — 3s2 1S0-3snp 3P1, n = 6—8 0.0006 — 3s2 1S0-3snp 1P1, n = 6—9 0.0184 — Others 0.1135 — Core 0.265 [19] 0.268 [27] VC –0.019 [19] — Total 24.1169 24.048 [19]
24.1396 [27]$ \alpha \left(0\right)( $3s2 1S0$ ) $ 3s3p 3P0-3s4s 3S1 2.1886 2.197 [19]
2.1860 [27]3s3p 3P0-3p2 3P1 8.7226 8.687 [19]
8.6830 [27]3s3p 3P0-3s3d 3D1 12.5817 12.568 [19]
12.6533 [27]3s3p 3P0-3s5s 3S1 0.1281 — 3s3p 3P0-3s4d 3D1 0.3451 — 3s3p 3P1-3sns 3S1, n = 6—9 0.0656 — 3s3p 3P1-3snd 3D1, n = 5—8 0.0855 — Others 0.2117 — Core 0.256 [19] 0.268 [27] VC –0.010 [19] — Total 24.5840 24.543 [19] $ {{\Delta }}\alpha \left(0\right) $ 0.467 0.495 [19]
0.482 [27]
0.426Expt.[4]
DownLoad: CSV
表 4 在“幻零”波长$ {\lambda }_{0} $处相关跃迁对两个光钟态3s2 1S0和3s3p 3P0的动力学极化率α($ {\lambda }_{0} $)的贡献
Table 4. Breakdown of the contributions of individual transitions to the dynamic polarizabilities α($ {\lambda }_{0} $) at the “tune-out” wavelengths $ {\lambda }_{0} $, for the 3s2 1S0 and 3s3p 3P0 clock states of Al+.
3s2 1S0 3s3p 3P0 $ {\lambda }_{0} $/nm 266.994(1) 184.56(7) 174.4(1) 121.5(1) 119.7(2) $ {\omega }_{0} $/a.u. 0.170653(2) 0.24688(7) 0.26171(15) 0.3750(3) 0.3806(6) $ {\alpha }_{0}\left({\lambda }_{0}\right)( $3s2 1S0$ ) $ 3s2 1S0-3s3p 3P1 –39.3927 –0.0003 0.0003 –9.1×10–5 –8.7×10–5 3s2 1S0-3s3p 1P1 39.0038 131.4864 287.4679 –26.6523 –25.0333 3s2 1S0-3s4p 3P1 7.5×10–6 8.9×10–6 9.3×10–6 1.7×10–5 1.8×10–5 3s2 1S0-3s4p 1P1 0.0033 0.0039 0.0041 0.0071 0.0074 3s2 1S0-3s5p 3P1 3.3×10–5 3.7×10–5 3.8×10–5 5.3×10–5 5.4×10–5 3s2 1S0-3s5p 1P1 0.0056 0.0062 0.0064 0.0089 0.0091 3s2 1S0-3snp 3P1, n = 6—8 0.0007 0.0008 0.0008 0.0010 0.0010 3s2 1S0-3snp 1P1, n = 6—9 0.0198 0.0216 0.0221 0.0281 0.0285 Others 0.1135 0.1135 0.1135 0.1135 0.1135 Core 0.265 0.265 0.265 0.265 0.265 VC –0.019 –0.019 –0.019 –0.019 –0.019 Total 0 131.8781 287.8605 –26.2478 –24.6278 $ {\alpha }_{0}\left({\lambda }_{0}\right)( $3s3p 3P0$ ) $ 3s3p 3P0-3s4s 3S1 4.2349 –195.2541 –16.5755 –1.6425 –1.5594 3s3p 3P0-3p2 3P1 15.4522 98.4756 –429.0192 –7.9128 7.4784 3s3p 3P0-3s3d 3D1 21.4976 95.2803 444.0076 –12.5559 –11.8356 3s3p 3P0-3s5s 3S1 0.1612 0.2245 0.2466 12.9773 –6.3146 3s3p 3P0-3s4d 3D1 0.4305 0.5901 0.6448 8.1466 26.1561 3s3p 3P1-3sns 3S1, n = 6—9 0.0765 0.0936 0.0987 0.2203 0.2388 3s3p 3P1-3snd 3D1, n = 5—8 0.1001 0.1234 0.1303 0.3005 0.3264 Others 0.2117 0.2117 0.2117 0.2117 0.2117 Core 0.265 0.265 0.265 0.265 0.265 VC –0.010 –0.010 –0.010 –0.010 –0.010 Total 42.4197 0 0 0 0
DownLoad: CSV
-
[1] Chaudhuri R K, Das B P, Freed K F 1998 J. Chem. Phys. 108 2556
Google Scholar
[2] Dong H, Jiang J, Wu Z W, Dong C Z, Gaigalas G 2021 Chin. Phys. B 30 043103
Google Scholar
[3] Zhang T X, Li J G, Liu J P 2018 Acta Phys. Sin. 67 053101 (in Chinese ) [张婷贤, 李冀光, 刘建鹏 2018 67 053101]
Google Scholar
Zhang T X, Li J G, Liu J P 2018 Acta Phys. Sin. 67 053101 (in Chinese )
Google Scholar
[4] Brewer S M, Chen J S, Hankin A M, Clements E R, Chou C W, Wineland D J, Hume D B, Leibrandt D R 2019 Phys. Rev. Lett. 123 033201
Google Scholar
[5] Cui K F, Chao S J, Sun C L, et al. 2022 Eur. Phys. J. D 76 140
Google Scholar
[6] Keller J, Burgermeister T, Kalincev D, et al. 2019 Phys. Rev. A 99 013405
Google Scholar
[7] Mitroy J, Safronova M S, Clark C W 2010 J. Phys. B: At. Mol. Opt. Phys. 43 202001
Google Scholar
[8] Kar S, Wang Y S, Wang Y, Ho Y K 2018 Can. J. Phys. 96 633
Google Scholar
[9] Cheng Y J, Jiang J, Mitroy J 2013 Phys. Rev. A 88 022511
Google Scholar
[10] Jiang J, Tang L Y, Mitroy J 2013 Phys. Rev. A 87 032518
Google Scholar
[11] Yu W W, Yu R M, Cheng Y J 2015 Chin. Phys. Lett. 32 123102
Google Scholar
[12] Yu W W, Yu R M, Cheng Y J, Zhou Y J 2016 Chin. Phys. B 25 023101
Google Scholar
[13] Safronova M S, Zuhrianda Z, Safronova U I, Clark C W 2015 Phys. Rev. A 92 040501(R
Google Scholar
[14] Holmgren W F, Trubko R, Hromada I, Cronin A D 2012 Phys. Rev. lett. 109 243004
Google Scholar
[15] Herold C D, Vaidya V D, Li X, Rolston S L, Porto J V, Safronova M S 2012 Phys. Rev. Lett. 109 243003
Google Scholar
[16] Reader J, Acquista N, Sansonetti C J, Sansonetti J E 1990 Astrophys. J. Suppl. Ser. 72 831
Google Scholar
[17] Samain D 1995 Astron. Astrophys. Suppl. Ser. 113 237
[18] Morton D C 1991 Astrophys. J. Suppl. Ser. 77 119
Google Scholar
[19] Safronova M S, Kozlov M G, Clark C W 2011 Phys. Rev. Lett. 107 143006
Google Scholar
[20] Tang Z M, Yu Y M, Jiang J, Dong C Z 2018 J. Phys. B: At. Mol. Opt. Phys. 51 125002
Google Scholar
[21] Wu L, Wang Xia, Wang T, Jiang J, Dong C Z 2023 New J. Phys. 25 043011
Google Scholar
[22] Dzuba V A, Flambaum V V, Kozlov M G 1996 Phys. Rev. A 54 3948
Google Scholar
[23] Kozlov M G, Porsev S G, Safronova M S, Tupitsyn I I 2015 Comput. Phys. Commun. 195 199
Google Scholar
[24] Tang Z M, Yu Y M, Dong C Z 2018 Chin. Phys. B 27 063101
Google Scholar
[25] Kramida A, Ralchenko Yu, Reader J, NIST ASD Team 2020 NIST Atomic Spectra Database (ver. 5.8) [Online]. Available: https://physics.nist.gov/asd. National Institute of Standards and Technology, Gaithersburg, MD
[26] Kumar R, Chattopadhyay S, Angom D, Mani B K 2021 Phys. Rev. A 103 022801
Google Scholar
[27] Mitroy J, Zhang J Y, Bromley M W J, Rollin R G 2009 Eur. Phys. J. D 53 15
Google Scholar
[28] Johnson W R, Safronova M S, Safronova U I 1997 Phys. Scr. 56 252
Google Scholar
[29] Stanek M, Glowacki L, Migdalek J 1996 J. Phys. B: At. Mol. Opt. Phys. 29 2985
Google Scholar
[30] Das B P, Idrees M 1990 Phys. Rev. A 42 6900
Google Scholar
[31] Fischer C F 2009 Phys. Scr. T134 014019
Google Scholar
[32] Ekman J, Godefroid M R, Hartman H 2014 Atoms 2 215
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 1980
- PDF Downloads: 122
- Cited By: 0
