-
We investigate the boundary effect of small-scale $ \text{s} $ quark matter, and the self-similarity structure influence of strange hadrons in the hadron gas on QGP–hadron phase transition. In this study, the multiple reflection expansion method is employed to investigate the boundary effect of QGP droplets containing $ \text{s} $ quarks. The calculation reveals that under the influence of boundary effect, small-scale $ \text{s} $ quark matter exhibits lower energy density, entropy density, and pressure. In hadron phase, there is the two-body self-similarity structure between $ \text{K} $ meson and neighboring π mesons under the influence of collective flow, quantum correlations, and strong interactions. By applying Two-Body Fractal Model to study the self-similarity structure of the $ \text{K} $ meson in meson and quark aspect, it is found that the self-similarity structure of the $ \text{K} $ meson exists in hadron phase, leading to an increase in the energy density, entropy density, and pressure of the $ \text{K} $ meson. With the influence of self-similarity structure, it is found that the derived transverse momentum spectrum of $ \text{K} $ meson has a good agreement with experimental data (Fig. (a)). This study predicts that in the HIAF energy region, the self-similarity structure factor of $ \text{K} $ meson $ q_{1} $ approaches $ 1.042 $. Under the influence of boundary effect and self-similarity structure of $ \text{K} $ and π mesons, it shows that the phase transition temperature of $ \text{s} $ quark matter increases (Fig. (b)). And if the boundary of $ \text{s} $ quark matter curves more, the increase of phase transition temperature becomes more pronounced compared to the influence of self-similarity structure.
-
Keywords:
- s quark /
- boundary effect /
- self-similarity structure /
- QCD phase transition
-
图 1 QGP热滴的势场示意图
Figure 1. The potential field of QGP droplet.
图 2 QGP热滴半径分别为$ r = 1, \, 1.5, \, 6\text{ fm} $的(a1)−(a3)能量密度; (b1)−(b3)熵密度; (c1)−(c3)压强
Figure 2. (a1)−(a3) Energy density; (b1)−(b3) entropy density and (c1)−(c3) pressure of QGP droplets with radius $ r = 1, \, 1.5, \, 6\text{ fm} $ respectively.
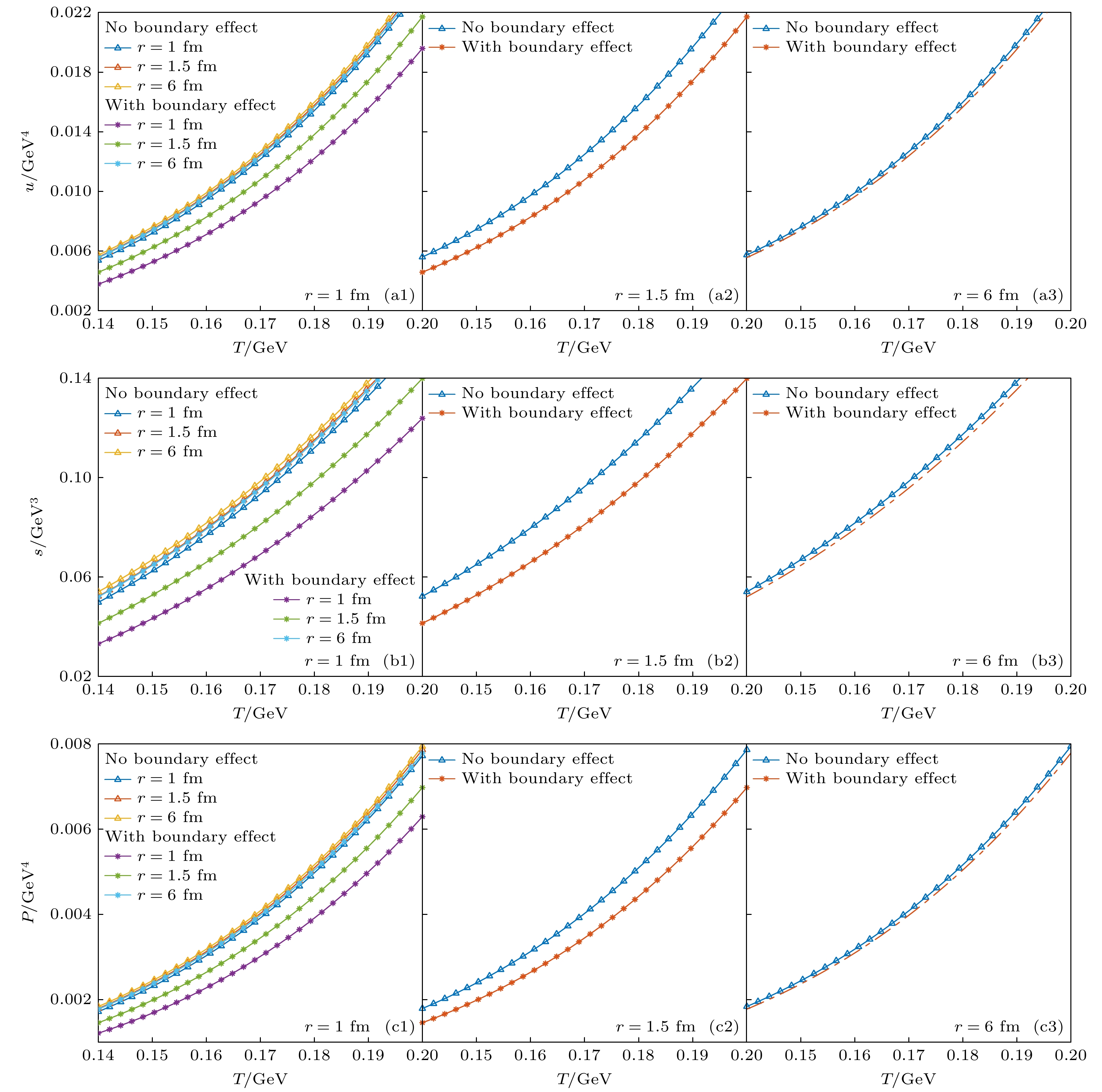
图 3 半径为$ r = 1\text{ fm} $的QGP热滴, 包含$ \text{s} $, $ \text{u} $, $ \text{d} $三种夸克, 和包含 $ \text{u} $, $ \text{d} $两种夸克的热力学量 (a)能量密度; (b)压强; (c)熵密度
Figure 3. Thermodynamic quantities of QGP droplet $ r = 1\text{ fm} $ considering $ \text{s} $, $ \text{u} $, $ \text{d} $ quarks and $ \text{u} $, $ \text{d} $ quarks in it respectively: (a) Energy density; (b) pressure; (c) entropy density.
图 4 (a) 介子层次和(b) 夸克层次下, 介子与介子-介子之间的自相似结构
Figure 4. Self-similarity structure of a meson and a resonant state in (a) meson aspect and (b) quark aspect.
图 5 Au+Au碰撞能量$ \sqrt{s_{\text{NN}}} = 39\text{ GeV} $中临界温度附近的两体自相似结构影响因子$ q_{1} $的变化
Figure 5. The relationship between the factor $ q_{1} $ and the temperature T near to the critical temperature in Au+Au collision at $ \sqrt{s_{\text{NN}}} = 39\, \text{GeV} $.
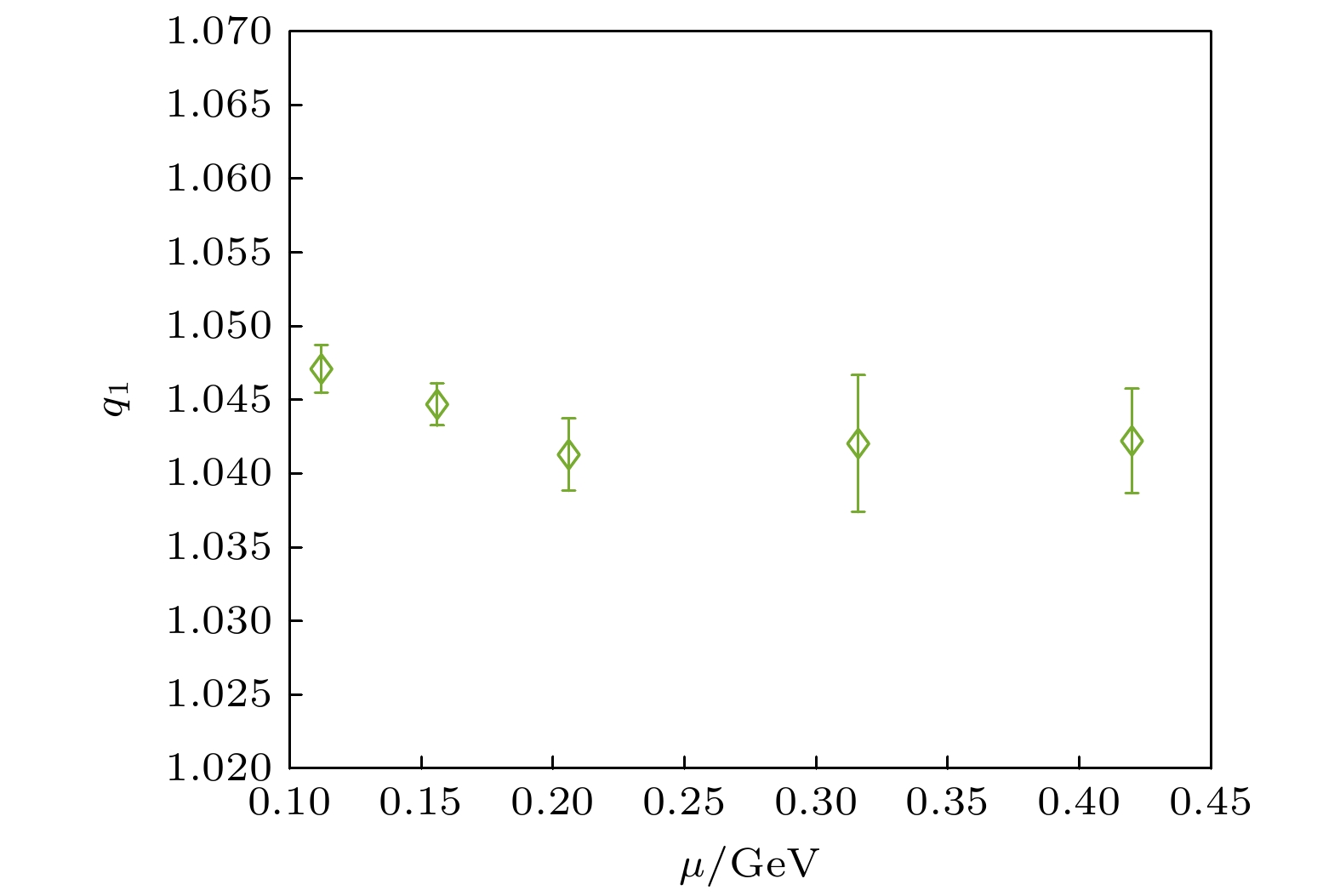
图 6 Au+Au碰撞能量$ \sqrt{s_{\text{NN}}} = 7.7, \, 11.5, \, 19.6, \, 27, $$ 39\text{ GeV} $, 0−5%对心度下, $ \text{K} $介子的自相似结构影响的修正因子$ q_{1} $和化学势的变化关系图
Figure 6. The relationship between the factor $ q_{1} $ for $ \text{K} $ meson and chemical potential μ in Au+Au collisions at $ \sqrt{s_{\text{NN}}} = 7.7, \, 11.5, \, 19.6, \, 27, \, 39\text{ GeV} $ for 0−5% centrality.
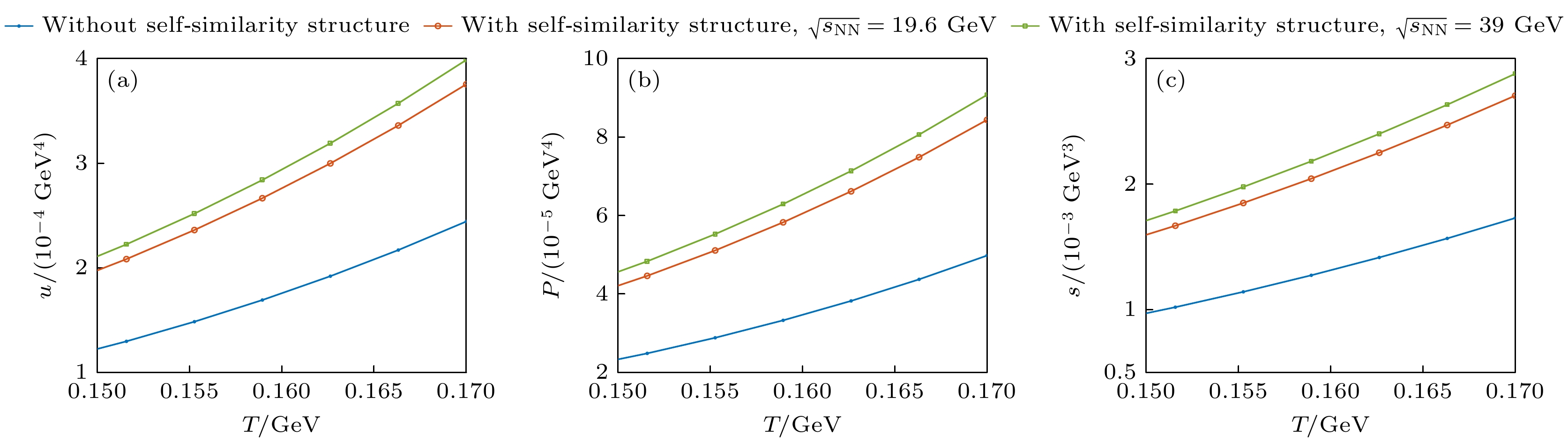
图 7 Au+Au碰撞能量$ \sqrt{s_{\text{NN}}} = 19.6, \, 39\text{ GeV} $中, 受自相似结构影响的$ \text{K} $介子的热力学量在临界相变温度时的变化: (a)能量密度; (b)压强; (c)熵密度
Figure 7. Thermodynamic quantities of kaon with and without the self-similarity structure influence in Au+Au collisions at $ \sqrt{s_{\text{NN}}} = 39, \, 19.6 \, \text{GeV} $ near the phase transition temperature: (a) energy density; (b) pressure; (c) entropy density.
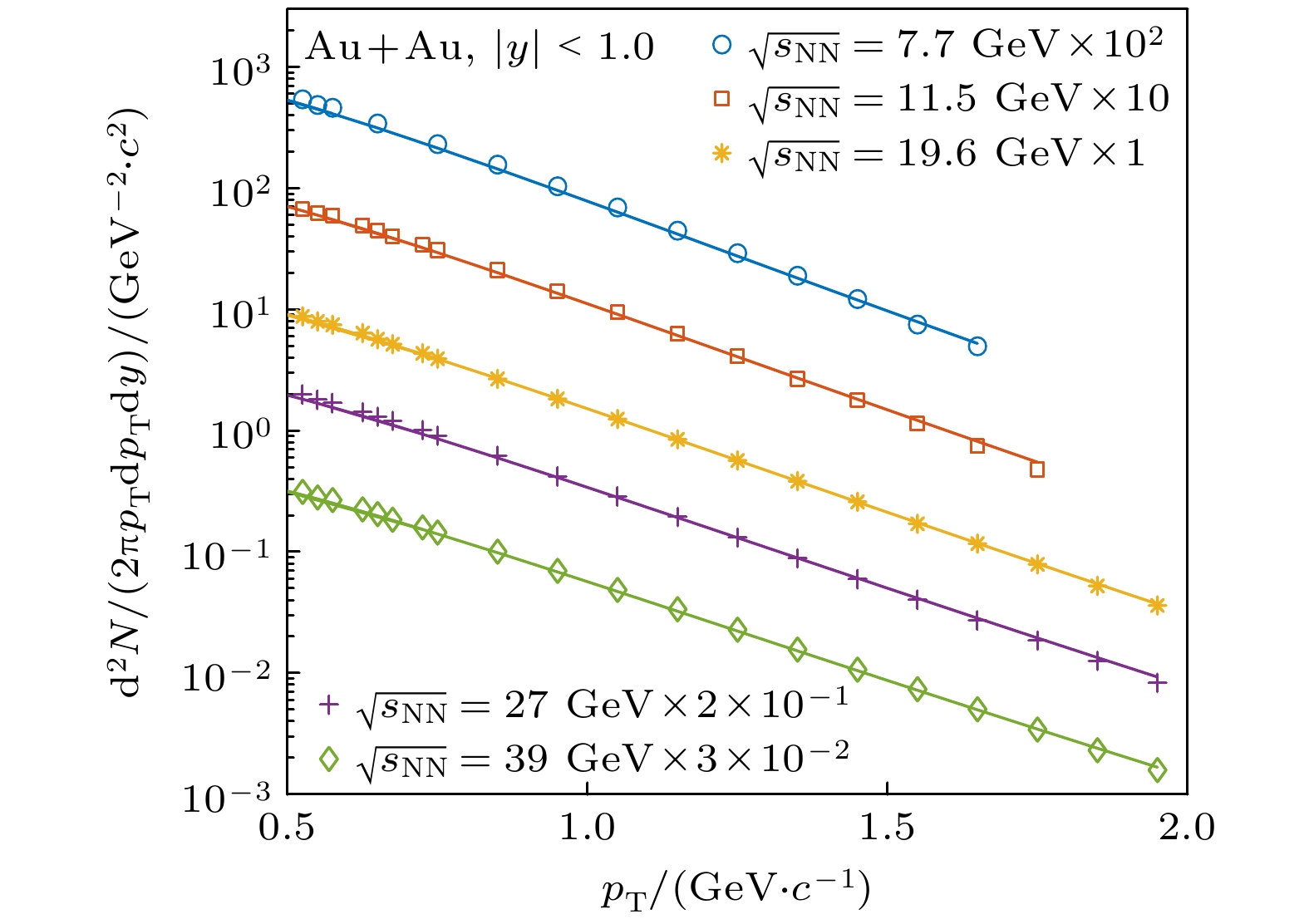
图 8 Au+Au碰撞能量$ \sqrt{s_{\text{NN}}} = 7.7, \, 11.5, \, 19.6, \; 27, $$ 39\text{ GeV} $, $ 0-5\% $对心度, $ |y| < 0.1 $下, $ \text{K} $介子受自相似结构影响下$ (\text{K}^{+}+\text{K}^{-})/2 $的横动量谱分布. 与之比对的实验数据来自STAR实验组[63]
Figure 8. Transverse momentum spectrum of $ (\text{K}^{+}+\text{K}^{-})/2 $ mesons in Au+Au collisions at $ \sqrt{s_{\text{NN}}} = 7.7, \, 11.5, \, 19.6,\; 27, $$ 39\text{ GeV} $ for $ 0-5\% $ centrality, in mid-rapidity $ |y| < 0.1 $. The experimental data are from STAR[63].
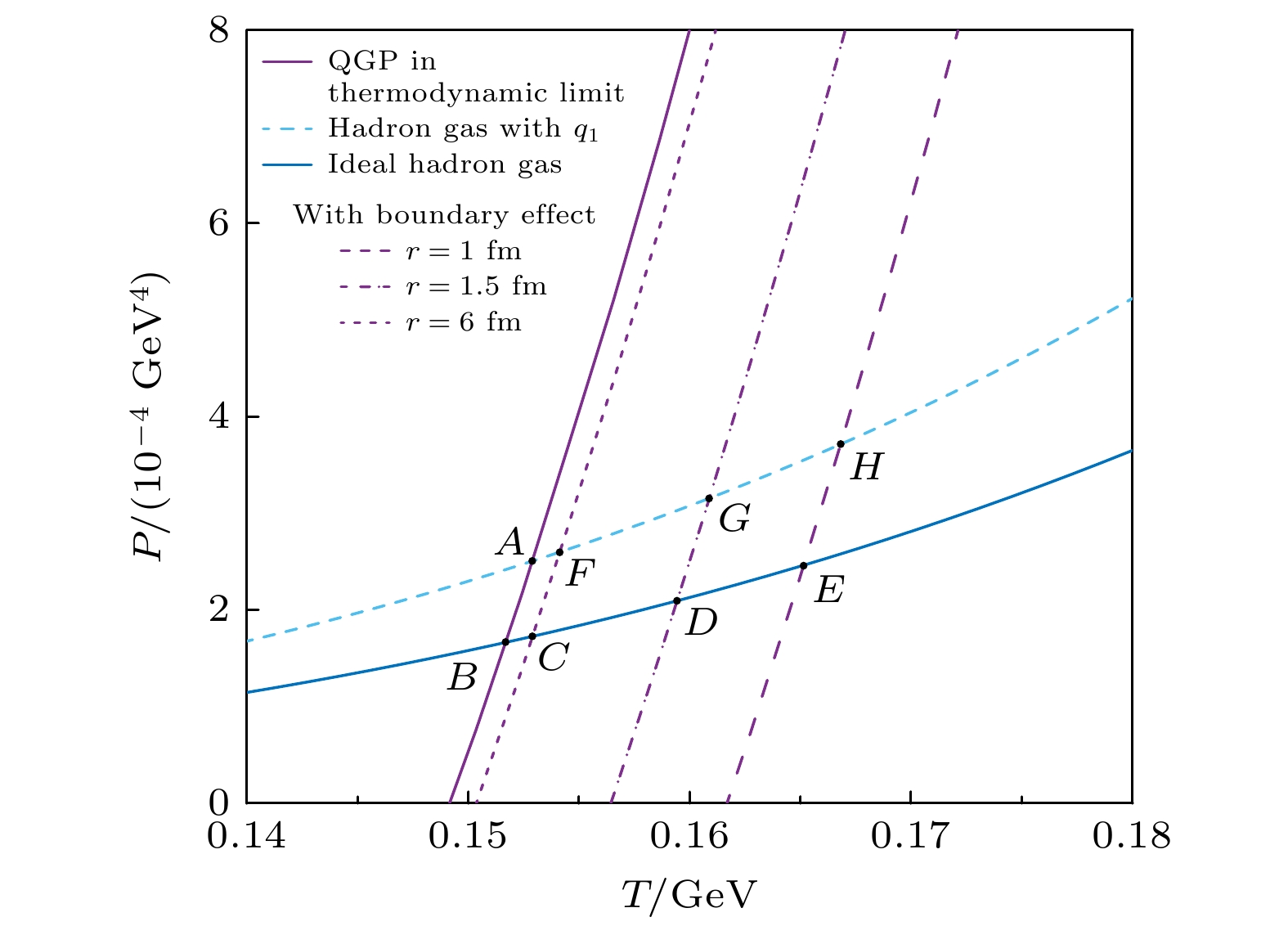
图 9 Au+Au碰撞能量$ \sqrt{s_{\text{NN}}} = 39\text{ GeV} $中, QGP热滴半径分别为$ r = 1, \, 1.5, \, 6\text{ fm} $的压强随温度的变化, 以及分别考虑强子气体为理想气体和受$ \text{K}, \pi $介子自相似结构影响的压强随温度的变化
Figure 9. The pressure in hadron phase with and without the influence of self-similarity structure on $ \text{K} $ and πmesons in Au+Au collisions at $ \sqrt{s_{\text{NN}}} = 39 \text{ GeV} $, and the pressure of QGP droplets at radius $ r = 1, \, 1.5, \, 6\text{ fm} $ as a function of temperature T.
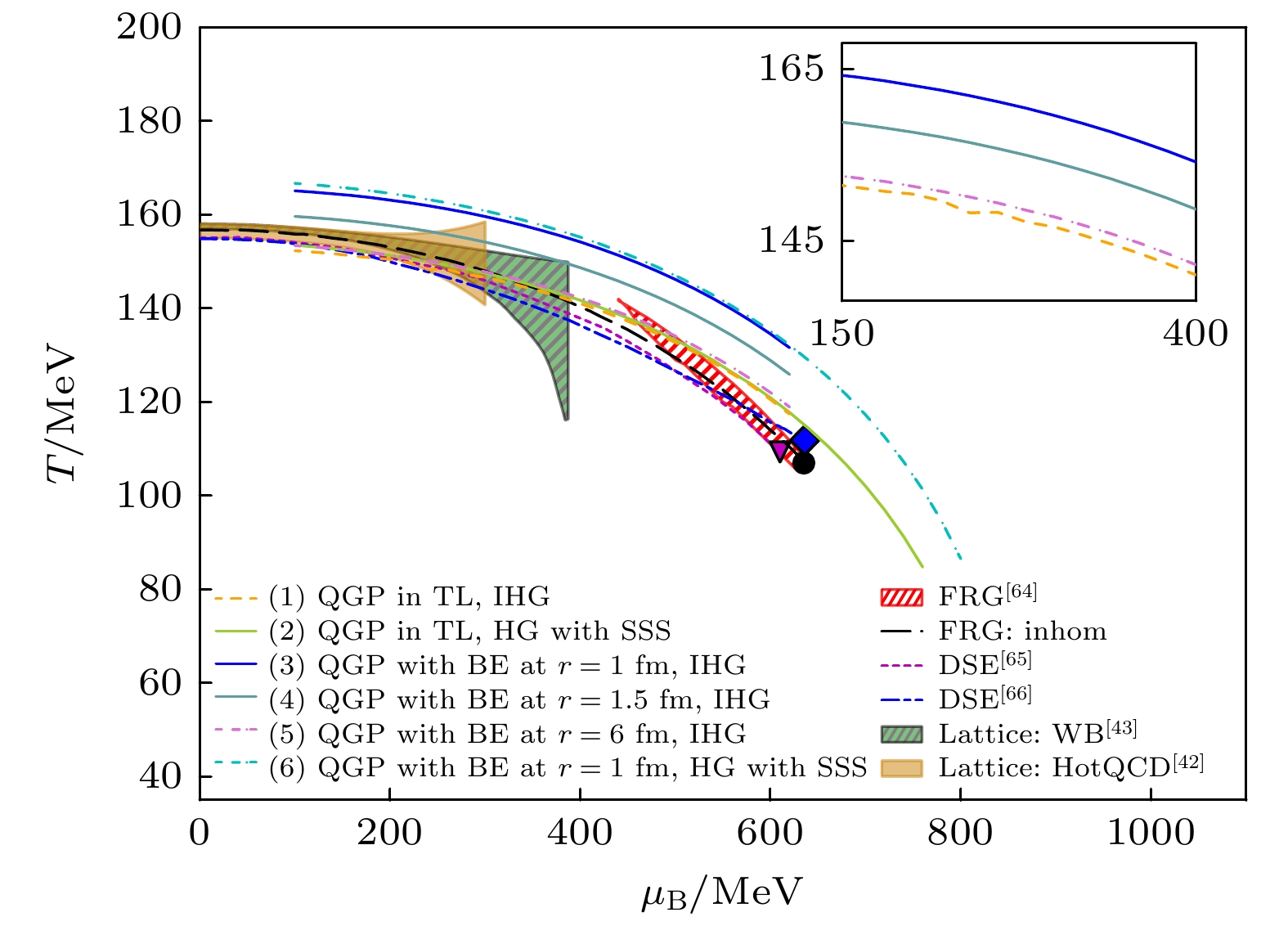
图 10 不同情况下的相图结果: (1) QGP相处于热力学极限(TL), 强子气体(HG)为理想气体(IHG); (2)QGP相处于热力学极限(TL), 强子气体受自相似结构影响; (3)(4)(5)QGP热滴半径分别为$ r = 1 \text{ fm}, 1.5 \text{ fm}, 6\text{ fm} $受边界效应(BE)影响, 强子气体为理想气体; (6)QGP热滴半径为$ r = 1 \text{ fm} $受边界效应影响, 强子气体受自相似结构影响. 我们也列出了泛函重整化群(fRG)方法[64], Dyson-Schwinger方程模型[65,66]和格点QCD[42,43]在有限化学势区域的相图结果, 以便比较
Figure 10. The phase diagram with considering (1) QGP in thermodynamic limit (TL) and ideal hadron gas (IHG). (2) QGP in thermodynamic limit and hadron gas (HG) with the influence of self-similarity structure (SSS). (3)(4)(5) QGP droplet with the boundary effect (BE) at radius $ r = 1 \text{ fm}, 1.5 \text{ fm}, 6\text{ fm} $ and ideal hadron gas(IHG) respectively. (6) QGP droplet with the boundary effect (BE) at radius $ r = 1 \text{ fm} $ and hadron gas with the influence of self-similarity structure (SSS). We also list the results from fRG model[64], DSE[65,66] and lattice QCD[42,43] for comparison.
表 1 Au+Au碰撞能量$ \sqrt{s_{\text{NN}}} = 7.7, \, 11.5, \, 19.6, \, 27, \, 39\text{ GeV} $, 0−5%对心度下, 通过TBFM方法求解出$ \text{K} $介子的自相似结构影响修正因子$ q_{1} $ 和 $ q_{2} $.
Table 1. The factors $ q_{1} $ and $ q_{2} $ for $ \text{K} $ meson in Au+Au collisions at $ \sqrt{s_{\text{NN}}} = 7.7, \, 11.5, \, 19.6, \, 27, \, 39 \text{ GeV} $ for 0−5% centrality solved by TBFM.
$ \sqrt{s_{\text{NN}}}/\text{GeV} $ $ T / \text{GeV} $ $ \mu_{\text{B}} / \text{GeV} $ $ r_{\text{min}}/\text{fm} $ $ r_{0}/\text{fm} $ $ q_{1} $ $ q_{2} $ 7.7 0.1424 $ \pm $ 0.00137 0.42 0.11 6.3 1.04222 $ \pm $ 0.003525 1.13941 $ \pm $ 0.010415 11.5 0.1483 $ \pm $ 0.00142 0.316 0.11 6.5 1.04204 $ \pm $ 0.004635 1.12682 $ \pm $ 0.01063 19.6 0.1527 $ \pm $ 0.00147 0.206 0.09 6.75 1.04129 $ \pm $ 0.002445 1.14432 $ \pm $ 0.005105 27 0.1541 $ \pm $ 0.00148 0.156 0.1 6.8 1.04470 $ \pm $ 0.001435 1.12251 $ \pm $ 0.00039 39 0.155 $ \pm $ 0.00149 0.112 0.1 6.85 1.04710 $ \pm $ 0.001615 1.11388 $ \pm $ 0.00012 
DownLoad: CSV
-
[1] Srivastava P K, Tiwari S K, Singh C P 2010 Phys. Rev. D 82 014023
Google Scholar
[2] Singh C 1993 Phys. Rep. 236 147
Google Scholar
[3] Satz H 2000 Rep. Prog. Phys. 63 1511
Google Scholar
[4] Back B, Baker M, Ballintijn M, et al 2005 Nucl. Phys. A 757 28
Google Scholar
[5] STAR Collaboration 2005 Nucl. Phys. A 757 102
Google Scholar
[6] Arsene I, Bearden I, Beavis D, et al 2005 Nucl. Phys. A 757 1
Google Scholar
[7] Karthein J M, Mroczek D, Acuna A R N, et al 2021 Eur. Phys. J. Plus 136 621
Google Scholar
[8] Mohanty B 2009 Nucl. Phys. A 830 899c
Google Scholar
[9] An X, Bluhm M, Du L, et al 2022 Nucl. Phys. A 1017 122343
Google Scholar
[10] Odyniec G 2019 PoS CORFU2018 201 151
[11] Bzdak A, Esumi S, Koch V, otehrs 2020 Phys. Rep. 853 1
Google Scholar
[12] Dai T, Ding H, Cheng L, Zhang W, Wang E 2024 arXiv: 2411.068219
[13] Deur A, Brodsky S J, de Téramond G F 2016 Prog. Part. Nucl. Phys. 90 1
Google Scholar
[14] Niida T, Miake Y 2021 AAPPS Bull. 31 12
Google Scholar
[15] Raghunath S 2019 AAPPS Bull. 29 16
[16] Loizides C 2016 Nucl. Phys. A 956 200
Google Scholar
[17] Shneider M N, Pekker M 2019 arXiv: 1901.04329
[18] Wong C Y, Zhang W N 2007 Int. J. Mod. Phys. E 16 3271
Google Scholar
[19] Gustafsson H A, Gutbrod H H, Kolb B, et al 1984 Phys. Rev. Lett. 52 1590
Google Scholar
[20] Danielewicz P, Odyniec G 1985 Phys. Lett. B 157 146
Google Scholar
[21] Wiranata A, Koch V, Prakash M, Wang X N 2014 J. Phys.: Conf. Ser. 509 012049
Google Scholar
[22] Zachariasen F, Zemach C 1962 Phys. Rev. 128 849
Google Scholar
[23] Rafelski J 1982 Phys. Rep 88 331
[24] Koch P, Müller B, Rafelski J 1986 Phys. Rep. 142 167
Google Scholar
[25] Greiner C, Koch P, Stöcker H 1987 Phys. Rev. Lett. 58 1825
Google Scholar
[26] Greiner C, Rischke D H, Stöcker H, Koch P 1988 Phys. Rev. D 38 2797
Google Scholar
[27] Greiner C, Stöcker H 1991 Phys. Rev. D 44 3517
Google Scholar
[28] Mønster D 1996 Strangelets: Effects of Finite Size and Exact Color Singletness. Ph.D. Dissertation, Aarhus University, Aarhus, Denmark
[29] Nordin F 2011 Quark-Gluon-Plasma at Brookhaven and CERN. Bachelor thesis, Lund University, Lund, Sweden
[30] STAR Collaboration 2020 Phys. Rev. C 102 034909
Google Scholar
[31] Moreau P, Soloveva O, Oliva L, Song T, Cassing W, Bratkovskaya E 2019 Phys. Rev. C 100 014911
Google Scholar
[32] Shen C, Alzhrani S 2020 Phys. Rev. C 102 014909
Google Scholar
[33] Albacete J L, Guerrero-Rodríguez P, Marquet C 2019 J. High Energy Phys. 2019 73
[34] Grönqvist H 2016 Fluctuations in High-Energy Particle Collisions. Theses, Université Paris Saclay (COmUE
[35] Chodos A, Jaffe R L, Johnson K, Thorn C B, Weisskopf V F 1974 Phys. Rev. D 9 3471
Google Scholar
[36] Ramanathan R, Gupta K K, Jha A K, Singh S S 2007 Pramana 68 757
Google Scholar
[37] Madsen J 1993 Phys. Rev. Lett. 70 391
Google Scholar
[38] Madsen J 1994 Phys. Rev. D 50 3328
Google Scholar
[39] Balian R, Bloch C 1970 Annals of Physics 60 401
Google Scholar
[40] Patra B K, Singh C P 1996 Phys. Rev. D 54 3551
Google Scholar
[41] Song G, Enke W, Jiarong L 1992 Phys. Rev. D 46 3211
Google Scholar
[42] Bazavov A, Ding H T, Hegde P, et al 2019 Phys. Lett. B 795 15
Google Scholar
[43] Bellwied R, Borsányi S, Fodor Z, Günther J, Katz S, Ratti C, Szabo K 2015 Phys. Lett. B 751 559
Google Scholar
[44] Hagedorn R 1971 Thermodynamics of strong interactions. Tech. rep., CERN
[45] Wong C Y 2002 Phys. Rev. C 65 034902
Google Scholar
[46] Pathria R, Beale P D 2022 Formulation of quantum statistics. Fourth edition edn. (Lodon: Elseviser), pp 117–154
[47] Musakhanov M 2017 EPJ Web Conf. 137 03013
Google Scholar
[48] Mandelbrot B B 1967 Science 156 636
Google Scholar
[49] Mandelbrot B B 1986 Self-affne fractal sets, I: The basic fractal dimensions (Amsterdam: Elsevier), pp 3–15
[50] Tsallis C 1988 J. Stat. Phys 52 479
Google Scholar
[51] Abe S, Okamoto Y 2001 Nonextensive statistical mechanics and its applications, vol. 560 (Berlin: Springer Science & Business Media), pp 5–6
[52] Ding H Q, Dai T T, Cheng L, Zhang W N, Wang E K 2023 Acta Phys. Sin. 72 192501
Google Scholar
[53] Ding H, Cheng L, Dai T, Wang E, Zhang W N 2023 Entropy 25 1655
Google Scholar
[54] Crater H W, Yoon J H, Wong C Y 2009 Phys. Rev. D 79 264
[55] Tsallis C 2009 Introduction to nonextensive statistical mechanics: approaching a complex world, vol. 1 (New York: Springer), pp 47–129
[56] Ubriaco M R 1999 Phys. Rev. E 60 165
Google Scholar
[57] Büyükkiliç F, Demirham D 1993 Phys. Lett. A 181 24
Google Scholar
[58] Feng X, Jin L, Riberdy M J 2022 Phys. Rev. Lett. 128 052003
Google Scholar
[59] Wang G, Liang J, Draper T, Liu K F, Yang Y B 2021 Phys. Rev. D 104 074502
Google Scholar
[60] Rajagopal A, Mendes R, Lenzi E 1998 Phys. Rev. Lett. 80 3907
Google Scholar
[61] Wang Q A 2002 Chaos, Solitons Fractals 14 765
Google Scholar
[62] Abe S 2001 Phys. Rev. E 63 061105
Google Scholar
[63] STAR Collaboration 2017 Phys. Rev. C 96 044904
Google Scholar
[64] Fu W J, Pawlowski J M, Rennecke F 2020 Phys. Rev. D 101 054032
Google Scholar
[65] Gao F, Pawlowski J M 2021 Phys. Lett. B 820 136584
Google Scholar
[66] Gunkel P J, Fischer C S 2021 Phys. Rev. D 104 054022
Google Scholar
DownLoad:
Metrics
- Abstract views: 401
- PDF Downloads: 4
- Cited By: 0
