-
In this paper, based on the steady solution of deep cellular crystal growth, the matching asymptotic method and multiple variable method are used to obtain the dispersion relation and the quantization condition of the interfacial morphology in directional solidification process when the interfacial dynamics is anisotropic. The stability of interfacial morphology of deep cell growth during directional solidification under the influence of anisotropic interfacial dynamics is studied. The mathematical model of the oriented solidification system is established, and the overall ground state solution of the constant cellular growth is taken as the ground state, and the unsteady state solution of the deep cellular growth is expressed as the superposition of the ground state solution and the perturbation dynamics solution when the stability analysis is carried out. The thermodynamic conditions in the mathematical model of the problem constitute a regenerative problem together with the boundary conditions. The asymptotic solution of the cellular crystal growth when $\varepsilon \to 0$ can be found by dividing the cellular crystal growth region into an outer region far from the root and a region near the root, with an asymptotic solution found in the external region and the root region, respectively, and then matching them to obtain a consistent and effective asymptotic solution in the whole region. The asymptotic solution of the model in the external region is derived to obtain a first-order approximation of the eigenvalues. The inner solutions are matched with the outer solutions based on the vicinity of the singularity to obtain the global solutions and quantization conditions of the system, and finally the stability analysis is conducted. The results show that the directional solidification system of deep cellular crystal growth considering anisotropic interfacial kinetics contains two global instability mechanisms: global oscillation instability and low-frequency instability. The stability analysis shows that the anisotropic interfacial kinetics has a significant effect on the global oscillatory instability mechanism in the low order approximation. With the increase of the anisotropic interfacial kinetics parameter${\beta _4}$ , the global oscillatory instability region$\left( {{\text{Os}}{\text{.U}}} \right)$ of the dendrite structure with strong oscillation in neutral mode decreases. At the same time, the influence of interfacial dynamic anisotropy parameters on the overall oscillation instability of the system increases with interfacial dynamic parameters increasing.-
Keywords:
- deep cellular crystal growth /
- interface kinetics /
- stability
[1] McFadden G B, Coriell S R 1984 Physica D 12 253
Google Scholar
[2] Hurle D 1993 Handbook of Crystal Growth (Vol. 1) (New York: Elsevier Science Publishers) pp899–1073
[3] Mullins W W, Sekerka R F 1963 Appl. Phys. 34 323
Google Scholar
[4] Mullins W W, Sekerka R F 1964 Appl. Phys. 35 444
[5] Langer J S 1980 Rev. Mod. Phys. 52 1
Google Scholar
[6] Pelcé P, Pumir A 1985 J. Cryst. Growth 73 337
Google Scholar
[7] Dombre T, Haankim V 1987 Phys. Rev. A 36 2811
Google Scholar
[8] Pelcé P 1988 Dynamics of Curved Fronts (New York: Academic Press) pp327–340
[9] Karma A, Pelcé P 1990 Phys. Rev. A 41 6741
[10] Benamar M, Bouissou P, Pelcé P 1988 J. Cryst. Growth 92 97
Google Scholar
[11] Xu J J 1991 Phys. Rev. A 43 930
Google Scholar
[12] Xu J J 1991 Eur. J. Appl. Math. 2 105
Google Scholar
[13] Xu J J 1996 Phys. Rev. E 53 5323
[14] Trivedi R, Seetharaman V, Eshelman M A 1991 Metall. Mater. Trans. A 22 585
Google Scholar
[15] Coriell S R, Sekerka R G 1976 J. Cryst. Growth 34 157
Google Scholar
[16] Young G W, Davis S H, Brattkus K 1987 J. Cryst. Growth 83 560
Google Scholar
[17] 袁训锋 2014 铸造技术 35 1773
Yuan X F 2014 Foundry Technol. 35 1773
[18] Zheng G J, Chen M W, Yang C M, Liu N 2022 Chin. J. Phys. 78 155
Google Scholar
[19] Zheng G J, Chen M W, Yang C M, Wang Z D 2022 Chin. J. Phys. 77 10
Google Scholar
[20] Chen K X, Demange G, Cui X, Wang Z D, Pang X L, Patte R, Mao H H, Chen X H, Shi R J, Zapolsky H 2024 Acta Mater. 270 119874
Google Scholar
[21] Pelcé P 1988 Dynamics of Curved Fronts (New York: Academic Press) pp155–174
[22] 陈明文, 陈奕臣, 张文龙, 刘秀敏, 王自东 2014 63 038101
Google Scholar
Chen M W, Chen Y C, Zhang W L, Liu X M, Wang Z D 2014 Acta Phys. Sin. 63 038101
Google Scholar
[23] Xu J J, Chen Y Q 2011 Phys. Rev. E 83 041601
[24] 钮迪, 蒋晗 2022 71 168101
Google Scholar
Niu D, Jiang H 2022 Acta Phys. Sin. 71 168101
Google Scholar
-
图 3 胞晶列界面图的尖端(A)和根部底端(B)
Figure 3. A sketch of cellular-line interface: The cellular tip (A) and the bottom of the root (B).
图 4 特征值随参数$\varepsilon $的变化曲线图 (a) 实部${\sigma _{\text{R}}}$; (b) 虚部$\omega $
Figure 4. Plot of eigenvalues with $\varepsilon $: (a) The real part ${\sigma _{\text{R}}}$; (b) the imaginary part $\omega $.
图 5 GTW-S中性模式曲线. 参数分别为$V = 16{\text{ μm/s}}, {\text{ }}{C_\infty } = $$ 1.2{\text{%}}, ~{G_T} = $ $78 \times {10^{ - 4}}{\text{ K/μm}},\; {\text{ }}{\varepsilon _{\text{c}}} = 0.5338 \times {10^{ - 2}},\; {\text{ }}M $= $0.09552,\; {\text{ }}k = 0.29, \;{\text{ }}{m_*} = 1, \;{\text{ }}{G_{\text{c}}} = 0.14485 \times {10^{ - 4}}, \;{\text{ }}{\lambda _G} $= $ 0.4989, {\text{ }}E = 0.25, {\text{ }}{\beta _4} = 0.6$ (a) 首级近似[24]; (b) 一级近似
Figure 5. The neutral curves of the GTW-S-modes for the case $V = 16{\text{ μm/s, }}\;{C_\infty } = 1.2{\text{%}},\; {\text{ }}{G_T}= 78 \;\times\; {10^{ - 4}}{\text{ K/μm}}, $ ${\varepsilon _{\text{c}}} = $$ 0.5338 \times {10^{ - 2}},\; {\text{ }}M = 0.09552,\; {\text{ }}k = 0.29, $ ${\text{ }}{m_*} = 1, {\text{ }}{G_{\text{c}}} = $$ 0.14485 \times {10^{ - 4}}, $ ${\lambda _G} = 0.4989, {\text{ }}E = 0.25, {\text{ }}{\beta _4} = 0.6$: (a) Leading-order approximation[24]; (b) first-order approximation.
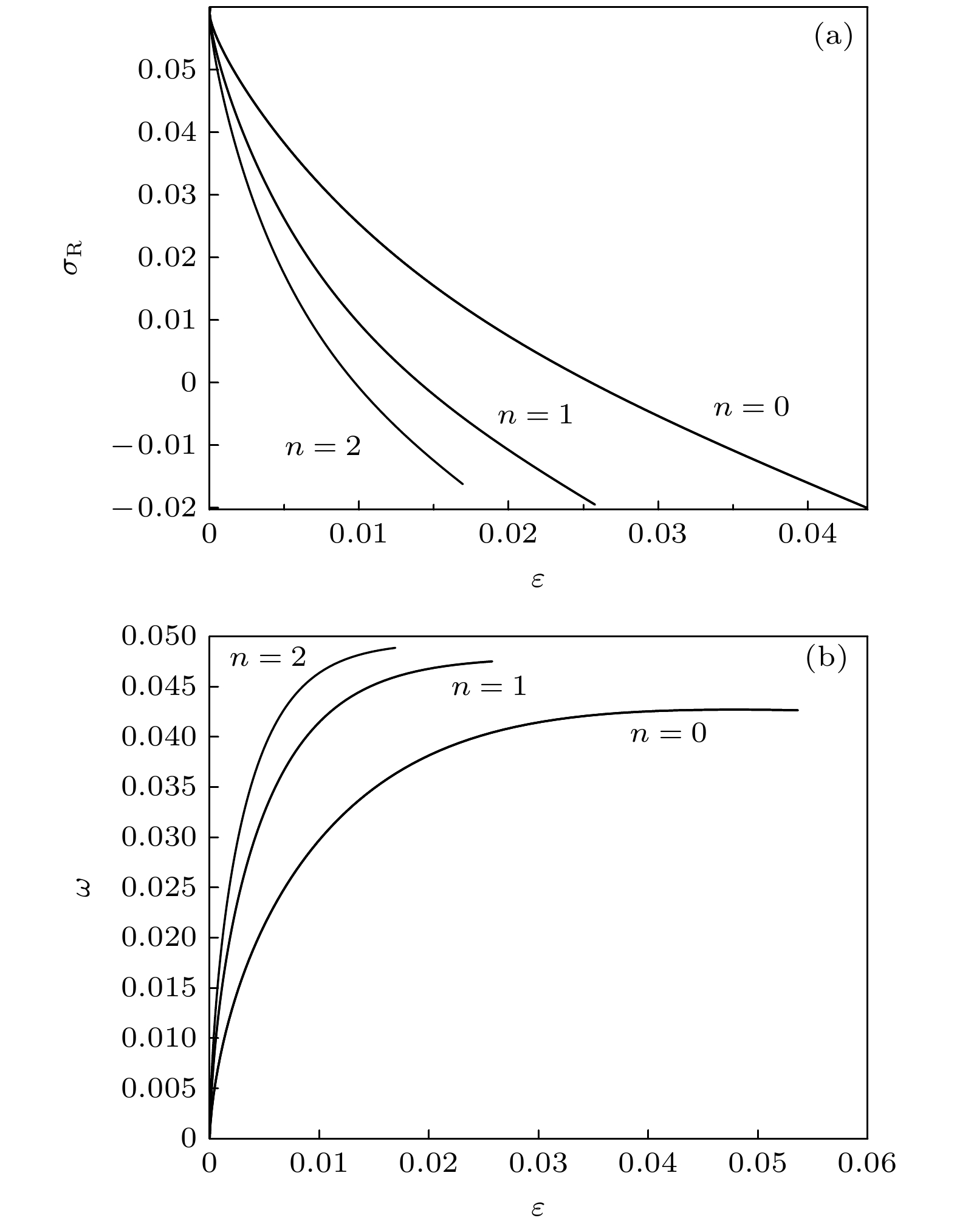
图 6 一级近似下的GTW-S中性模式曲线$\left( {n = 0} \right)$. 参数分别为${C_\infty } = 1.2{\text{%}}, {\text{ }}{G_T} =78 \times {10^{ - 4}}{\text{ K/μm}}, {\text{ }}V = 16{\text{ μm/s}},$ $ {\varepsilon _{\text{c}}} = 0.5338 \times {10^{ - 2}}, {\text{ }}M = 0.09552, {\text{ }}{G_{\text{c}}} = 0.14485 \times {10^{ - 4}} $, $k=0.29$, ${\lambda _G} = 0.4989$, $E = 0.25, {\text{ }}{m_*} = 5 $
Figure 6. The neutral curves of the GTW-S-modes $(n = 0)$in the first-order approximation for the case ${C_\infty } = 1.2{\text{%}}$, ${G_T} = 78 \times {10^{ - 4}}{\text{ K/μm}}$, $V = 16\;{\text{μm/s}}$, ${\varepsilon _{\text{c}}} = 0.005338$, $M= $$ 0.09552$, ${G_{\text{c}}} = 0.14485 \times {10^{ - 4}}$, $k = 0.29,\; {\lambda _G} = 0.4989$, $E= 0.25, \; {m_*} = 5 $
图 7 一级近似下的GTW-S中性模式曲线$\left( {n = 0} \right)$. 参数分别为${C_\infty }= 1.2{\text{%}}, {G_T} = 78 \times {10^{ - 4}}{\text{ K/μm, }}V = 16{\text{ μm/s }}, {\varepsilon _{\text{c}}} =$ $ 0.5338 \times {10^{ - 2}}, {\text{ }}M = 0.09552, {\text{ }}{G_{\text{c}}} $ = $0.14485 \times {10^{ - 4}},\; {\text{ }}k = $$ 0.29{, }\;{\lambda _G} = 0.4989,\; {\text{ }}E = 0.25$
Figure 7. The neutral curves of the GTW-S-modes $(n = 0)$in the first-order approximation. The case ${C_\infty } = 1.2{\text{%}}$, $ {G_T} = $$ 78 \times {10^{-4}}{\text{ K/μm}}, \; V = 16\;{\text{μm/s}}, \;{\varepsilon _{\text{c}}} = 0.005338,\; M = 0.09552$, ${G_{\text{c}}} = 0.14485 \times {10^{ - 4}}, \;k = 0.29, \;\lambda_G = 0.4989,$ E = 0.25
-
[1] McFadden G B, Coriell S R 1984 Physica D 12 253
Google Scholar
[2] Hurle D 1993 Handbook of Crystal Growth (Vol. 1) (New York: Elsevier Science Publishers) pp899–1073
[3] Mullins W W, Sekerka R F 1963 Appl. Phys. 34 323
Google Scholar
[4] Mullins W W, Sekerka R F 1964 Appl. Phys. 35 444
[5] Langer J S 1980 Rev. Mod. Phys. 52 1
Google Scholar
[6] Pelcé P, Pumir A 1985 J. Cryst. Growth 73 337
Google Scholar
[7] Dombre T, Haankim V 1987 Phys. Rev. A 36 2811
Google Scholar
[8] Pelcé P 1988 Dynamics of Curved Fronts (New York: Academic Press) pp327–340
[9] Karma A, Pelcé P 1990 Phys. Rev. A 41 6741
[10] Benamar M, Bouissou P, Pelcé P 1988 J. Cryst. Growth 92 97
Google Scholar
[11] Xu J J 1991 Phys. Rev. A 43 930
Google Scholar
[12] Xu J J 1991 Eur. J. Appl. Math. 2 105
Google Scholar
[13] Xu J J 1996 Phys. Rev. E 53 5323
[14] Trivedi R, Seetharaman V, Eshelman M A 1991 Metall. Mater. Trans. A 22 585
Google Scholar
[15] Coriell S R, Sekerka R G 1976 J. Cryst. Growth 34 157
Google Scholar
[16] Young G W, Davis S H, Brattkus K 1987 J. Cryst. Growth 83 560
Google Scholar
[17] 袁训锋 2014 铸造技术 35 1773
Yuan X F 2014 Foundry Technol. 35 1773
[18] Zheng G J, Chen M W, Yang C M, Liu N 2022 Chin. J. Phys. 78 155
Google Scholar
[19] Zheng G J, Chen M W, Yang C M, Wang Z D 2022 Chin. J. Phys. 77 10
Google Scholar
[20] Chen K X, Demange G, Cui X, Wang Z D, Pang X L, Patte R, Mao H H, Chen X H, Shi R J, Zapolsky H 2024 Acta Mater. 270 119874
Google Scholar
[21] Pelcé P 1988 Dynamics of Curved Fronts (New York: Academic Press) pp155–174
[22] 陈明文, 陈奕臣, 张文龙, 刘秀敏, 王自东 2014 63 038101
Google Scholar
Chen M W, Chen Y C, Zhang W L, Liu X M, Wang Z D 2014 Acta Phys. Sin. 63 038101
Google Scholar
[23] Xu J J, Chen Y Q 2011 Phys. Rev. E 83 041601
[24] 钮迪, 蒋晗 2022 71 168101
Google Scholar
Niu D, Jiang H 2022 Acta Phys. Sin. 71 168101
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 1298
- PDF Downloads: 41
- Cited By: 0
