-
The accurate measurement and calculation of molecular electron affinity has been a hot topic. The existing theoretical study does not consider the effects of different basic sets, or various correlation effects or zero point energy correction. In addition, there are some deviations of calculation results from experimental measurements. Therefore, we conduct a high-level ab initio study on the electron affinities of CO2, OCS, CS2 and their corresponding anions
$ {\text{CO}}_{2}^{{ - }} $ , OCS–,$ {\text{CS}}_{2}^{{ - }} $ by adopting the coupled cluster with singles and doubles (triples) (CCSD(T)), spin-unrestricted open-shell coupled cluster with singles and doubles (triples) (UCCSD(T)), respectively. The equilibrium geometries of the ground states of these molecules are calculated under a series of extended correlation consistent basis sets aug-cc-pV (X+d)Z (X = T, Q, 5) and complete basis set extrapolation (CBS) limit. The effects of core-valence (CV) electron correlation and scalar relativistic (SR) on equilibrium geometry of the ground state are studied, and our results are compared with previous experimental observations and theoretical data. Our calculations are in good agreement with the previous results. It is found that the calculations of equilibrium geometries of these molecules tend to converge. It is noted that the scalar relativistic effect has little influence on the equilibrium structure of the neutral molecule, but it has more significant influence on the bond angle of$ {\text{CS}}_{2}^{{ - }} $ .With the increase of atomic number, the core-valence correlation effect exerts a more remarkable influence on the equilibrium structures of ground states of CS2 and$ {\text{CS}}_{2}^{{ - }} $ molecules except for RC-S of OCS–. Based on accurate structures, the adiabatic energy values of neutral molecules CO2, OCS, CS2 by CCSD(T) method and those of$ {\text{CO}}_{2}^{{ - }} $ , OCS–,$ {\text{CS}}_{2}^{{ - }} $ by using UCCSD(T) and spin-restricted open-shell coupled cluster with singles and doubles (triples) (RCCSD(T)) are calculated, respectively. And finally, the adiabatic electron affinities (EAs) of the neutral molecules CO2, OCS, CS2 are obtained. The effects of different basis sets, CBS, correlation effects and zero-point energy correction on the EA values of these molecules are investigated. It is found that both the scalar relativistic effect and the core-valence correlation effect affect the EAs of neutral molecules, and the core-valence correlation effect has a more significant effect on the EA value. The results show that the correlation effect has more significant influence on the adiabatic EA than the equilibrium structure of the ground state of neutral molecules. Based on the CBS+ΔCV+ΔDK+ΔZPE calculation, accurate EA information is acquired. Our results of EA values are within the experimental error. This work will enrich the information about spectral constants and electron affinities of carbon-containing triatomic molecules, and provide an important reference for experimental spectral analysis.-
Keywords:
- coupled cluster method /
- carbon-containing triatomic molecules /
- equilibrium geometry /
- electron affinities
[1] Rienstra K J C, Tschumper G S, Schaefer H F, Nandi S, Ellison G B 2002 Chem. Rev. 102 231
Google Scholar
[2] Cahen D, Kahn A 2003 Adv. Mater. 15 271
Google Scholar
[3] Ru P B, Bi E, Zhang Y, Wang Y B, Kong W Y, Tang W T, Zhang P, Wu Y Z, Chen W, Yang X D, Chen H, Han L Y 2020 Adv. Energy Mater. 10 1903487
Google Scholar
[4] Compton R N, Reinhardt P W, Cooper C D 1975 J. Chem. Phys. 63 3821
Google Scholar
[5] Holroyd R A, Cangwer T E, Allen A O 1975 Chem. Phys. Lett. 31 520
Google Scholar
[6] Surber E, Sanov A 2002 J. Chem. Phys. 116 5921
Google Scholar
[7] Chen E C M, Wentworth W E 1983 J. Phys. Chem. 87 45
Google Scholar
[8] Hughes B M, Lifshitzt C, Tiernan T O 1973 J. Chem. Phys. 59 3162
Google Scholar
[9] Oakes J M, Barney Ellison G 1986 Tetrahedron. 42 6263
Google Scholar
[10] Schiedt J, Weinkauf R 1997 Chem. Phys. Lett. 274 18
Google Scholar
[11] Misaizu F, Tsunoyama H, Yasumura Y, Ohshimo K, Ohno K 2004 Chem. Phys. Lett. 389 241
Google Scholar
[12] Cavanagh S J, Gibson S T, Lewis B R 2012 J. Chem. Phys. 137 144304
Google Scholar
[13] Herzberg G 1966 Molecular Spectra & Molecular Structure III (Polyatomic Molecules) (New York: Van Nostrand Reinhold) p145
[14] Hartman K O, Hisatsune I C 1966 J. Chem. Phys. 44 1913
Google Scholar
[15] Ovenall D W, Whiffen D H 1961 Mol. Phys. 4 135
Google Scholar
[16] Lahaye J G, Vandenhaute R, Fayt A 1987 J. Mol. Spectrosc. 123 48
Google Scholar
[17] Suzuki I 1975 Bull. Chem. Soc. Jpn. 48 1685
Google Scholar
[18] Bennett J E, Mile B, Thomas A 1967 Trans. Faraday Soc. 63 262
Google Scholar
[19] Yu D, Rauk A, Armstrong D A 1992 J. Phys. Chem. 96 6031
Google Scholar
[20] Gutsev G L, Bartlett R J, Compton R N 1998 J. Chem. Phys. 108 6756
Google Scholar
[21] Barsotti S, Sommerfeld T, Ruf M W, Hotop H 2004 Int. J. Massspectrom. 233 181
[22] Pacansky J, Wahlgren U, Bagus P S 1975 J. Chem. Phys. 62 2740
Google Scholar
[23] Yoshioka Y, Schaefer H F, Jordan K D 1981 J. Chem. Phys. 75 1040
Google Scholar
[24] Surber E, Ananthavel S P, Sanov A 2002 J. Chem. Phys. 116 1920
Google Scholar
[25] Joachim W H, Knowles P J, Knizia G, Manby F R, Schütz M 2012 Wiley Interdiscip. Rev. : Comput. Mol. Sci. 2 242
Google Scholar
[26] Bartlett R J, Watts J D, Kucharski S A, Noga J 1990 Chem. Phys. Lett. 165 513
Google Scholar
[27] Dunning T H, Peterson K A, Wilson A K 2001 J. Chem. Phys. 114 9244
Google Scholar
[28] Fellera D, Peterson K A, Daniel C T 2006 J. Chem. Phys. 124 054107
Google Scholar
[29] Fellera D, Peterson K A 2007 J. Chem. Phys. 126 114105
Google Scholar
[30] Peterson K A, Woon D E, Dunning T H 1994 J. Chem. Phys. 100 7410
Google Scholar
[31] Dunning T H 1989 J. Chem. Phys. 90 1007
Google Scholar
[32] Reiher M, Wolf A 2004 J. Chem. Phys. 121 2037
Google Scholar
[33] Wolf A, Reiher M, Hess B A 2002 J. Chem. Phys. 117 9215
Google Scholar
[34] Peterson K A, Dunning T H 2002 J. Chem. Phys. 117 10548
Google Scholar
[35] Lu T, Chen F W 2012 J. Comput. Chem. 33 580
Google Scholar
-
图 1 (a) CO2基态分子轨道图; (b) OCS基态分子轨道图; (c) CS2基态分子轨道图
Figure 1. (a) Molecular orbital of the ground state of CO2; (b) molecular orbital of the ground state of OCS; (c) molecular orbital of the ground state of CS2.
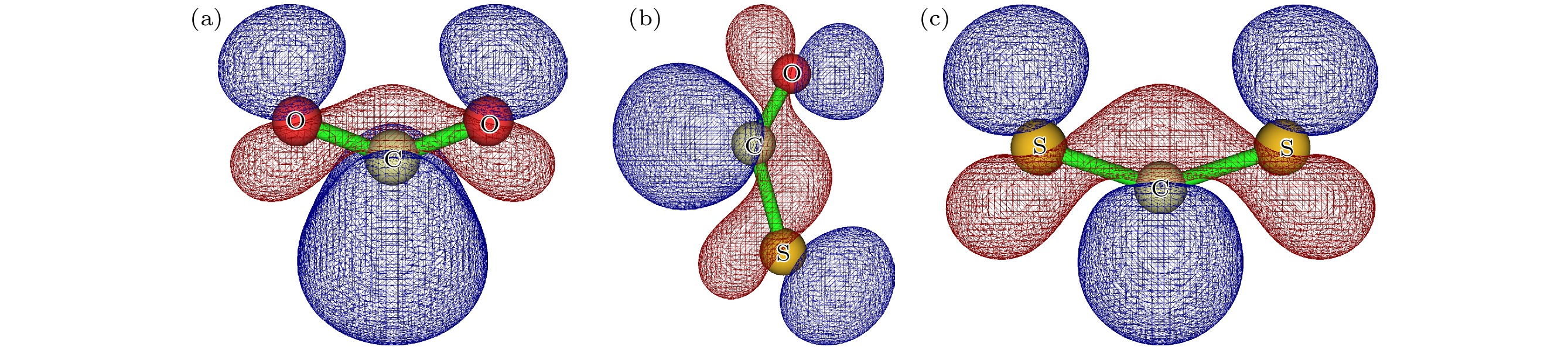
图 2 (a) $ {\text{CO}}_2^ - $基态分子轨道图; (b) $ {\mathrm{OC{S}}^ - } $基态分子轨道图; (c) $ {\mathrm{C}}{\text{S}}_2^ - $基态分子轨道图
Figure 2. (a) Molecular orbital of the ground state of $ {\text{CO}}_2^ - $; (b) molecular orbital of the ground state of $ {\mathrm{OC{S}}^ - } $; (c) molecular orbital of the ground state of $ {\mathrm{C}}{\text{S}}_2^ - $.
表 1 CO2, OCS, CS2及其阴离子在不同基组与CBS极限下基态的键长与键角
Table 1. Equilibrium bond distance and bond angle of the ground state of CO2, OCS, CS2 and the corresponding anions as a function of different basis sets and CBS limit.
AV(T+d)Z AV(Q+d)Z AV(5+d)Z CBS CO2 RC-O/Å 1.167 1.163 1.162 1.162 ${\text{CO}}_2^ - $ RC-O/Å 1.237 1.232 1.231 1.230 ∠OCO/(°) 137.6 137.7 137.8 137.9 OCS RC-O/Å 1.163 1.159 1.158 1.158 RC-S/Å 1.571 1.567 1.566 1.565 ${\mathrm{OCS}}^{ - } $ RC-O/Å 1.214 1.210 1.209 1.208 RC-S/Å 1.710 1.705 1.703 1.701 ∠OCS/(°) 136.5 136.4 136.5 136.5 CS2 RC-S/Å 1.562 1.558 1.557 1.555 $ {\text{CS}}_{2}^{{ - }} $ RC-S/Å 1.641 1.636 1.634 1.633 ∠SCS/(°) 143.3 143.5 143.6 143.7 
DownLoad: CSV
表 2 CO2, OCS, CS2及其应阴离子在不同关联效应下基态的键长与键角
Table 2. Equilibrium bond distance and bond angle of the ground state of CO2, OCS, CS2 and the corresponding anions as a function of different correlation effect.
本工作计算结果 其他计算结果 实验结果 CBS ΔCV ΔDK Total CO2 R C-O/Å 1.162 –0.002 0 1.160 1.143 [19]/1.179 [19]/1.1614 [20]/1.164 [20]/1.167 [21] 1.162 [13] $ {\text{CO}}_{2}^{{ - }} $ R C-O/Å 1.230 –0.002 0 1.228 1.225 [19]/1.256 [19]/1.230 [20]/1.233 [20]/1.237 [21] 1.25 [14] ∠OCO/(°) 137.9 0.1 0 138.0 135 [19]/134.2 [19]/137.9 [20]/137.7 [20]/136.7 [21] 134 [15] OCS R C-O/Å 1.158 –0.002 0 1.156 1.158 [20]/1.161 [20])/1.163 [21] 1.156 [16] R C-S/Å 1.565 –0.003 0 1.562 1.566 [20]/1.563 [20]/1.575 [21] 1.561 [16] ${\mathrm{OCS}}^{ - } $ R C-O/Å 1.208 –0.002 0 1.206 1.208 [20]/1.209 [20]/1.213 [21] — R C-S/Å 1.701 –0.005 0 1.696 1.704 [20]/1.707 [20]/1.716 [21] — ∠OCS/(°) 136.5 0.1 0 136.6 136.5 [20]/136.3 [20]/136.2 [21] — CS2 R C-S/Å 1.555 –0.003 0 1.552 1.558 [20]/1.557 [20]/1.565 [21] 1.556 [17] $ {\text{CS}}_{2}^{{ - }} $ R C-S/Å 1.633 –0.004 0 1.629 1.635 [20]/1.630 [20]/1.646 [21] — ∠SCS/(°) 143.7 0.2 –0.1 143.8 144 [20]/145.2 [20]/142.7 [21] 141 [18]
DownLoad: CSV
表 3 CO2分子的绝热电子亲和能以及与以往理论和实验数据对比
Table 3. Adiabatic electron affinity of CO2 compared to previous theoretical and experimental data.
绝热电子亲和能/eV UCCSD(T) RCCSD(T) AV(T+d)Z –0.631 –0.654 AV(Q+d)Z –0.630 –0.653 AV(5+d)Z –0.624 –0.648 Q5-CBS –0.616 –0.640 TQ5-CBS –0.619 –0.643 ΔCV –0.012 ΔDK –0.003 ΔZPE 0.090 Total –0.541a)/–0.544b) –0.565a)/–0.568b) Experiment –0.6 ± 0.2 [4]/–0.44±0.2 [5] Calculation –0.36 [22]/–0.669 [20]/–0.544 [21] 注: a)Q5-CBS+ΔCV+ΔDK+ΔZPE result.
b)TQ5-CBS+ΔCV+ΔDK+ΔZPE result.
DownLoad: CSV
表 5 CS2分子的电子亲和能以及与以往理论和实验数据对比
Table 5. Adiabatic electron affinity of CS2 compared to previous theoretical and experimental data.
绝热电子亲和能/eV UCCSD(T) RCCSD(T) AV(T+d)Z 0.359 0.337 AV(Q+d)Z 0.399 0.377 AV(5+d)Z 0.407 0.384 Q5-CBS 0.417 0.394 TQ5-CBS 0.412 0.389 ΔCV –0.013 ΔDK –0.009 ΔZPE 0.053 Total 0.448 a)/0.443 b) 0.425 a)/0.420 b) Experiment 0.6 ± 0.1 [7]/≤0.8 [10]/0.58±0.05 [11]/
0.5525(13) [12]Calculation 0.406 [20]/0.382 [20]/0.457 [21]/0.54 [11] 注: a)Q5-CBS+ΔCV+ΔDK+ΔZPE result.
b)TQ5-CBS+ΔCV+ΔDK+ΔZPE result.
DownLoad: CSV
表 4 OCS分子的电子亲和能以及与以往理论和实验数据对比
Table 4. Adiabatic electron affinity of OCS compared to previous theoretical and experimental data.
绝热电子亲和能/eV UCCSD(T) RCCSD(T) AV(T+d)Z –0.098 –0.119 AV(Q+d)Z –0.073 –0.095 AV(5+d)Z –0.069 –0.091 Q5-CBS –0.062 –0.0839 TQ5-CBS –0.066 –0.0876 ΔCV –0.016 ΔDK –0.004 ΔZPE 0.070 Total –0.012 a)/–0.016 b) –0.034 a)/–0.038 b) Experiment 0.46±0.2 [4]/–0.04 [6] Calculation –0.007 [21]/–0.059±0.061 [24] 注: a)Q5-CBS+ΔCV+ΔDK+ΔZPE result.
b)TQ5-CBS+ΔCV+ΔDK+ΔZPE result.
DownLoad: CSV
-
[1] Rienstra K J C, Tschumper G S, Schaefer H F, Nandi S, Ellison G B 2002 Chem. Rev. 102 231
Google Scholar
[2] Cahen D, Kahn A 2003 Adv. Mater. 15 271
Google Scholar
[3] Ru P B, Bi E, Zhang Y, Wang Y B, Kong W Y, Tang W T, Zhang P, Wu Y Z, Chen W, Yang X D, Chen H, Han L Y 2020 Adv. Energy Mater. 10 1903487
Google Scholar
[4] Compton R N, Reinhardt P W, Cooper C D 1975 J. Chem. Phys. 63 3821
Google Scholar
[5] Holroyd R A, Cangwer T E, Allen A O 1975 Chem. Phys. Lett. 31 520
Google Scholar
[6] Surber E, Sanov A 2002 J. Chem. Phys. 116 5921
Google Scholar
[7] Chen E C M, Wentworth W E 1983 J. Phys. Chem. 87 45
Google Scholar
[8] Hughes B M, Lifshitzt C, Tiernan T O 1973 J. Chem. Phys. 59 3162
Google Scholar
[9] Oakes J M, Barney Ellison G 1986 Tetrahedron. 42 6263
Google Scholar
[10] Schiedt J, Weinkauf R 1997 Chem. Phys. Lett. 274 18
Google Scholar
[11] Misaizu F, Tsunoyama H, Yasumura Y, Ohshimo K, Ohno K 2004 Chem. Phys. Lett. 389 241
Google Scholar
[12] Cavanagh S J, Gibson S T, Lewis B R 2012 J. Chem. Phys. 137 144304
Google Scholar
[13] Herzberg G 1966 Molecular Spectra & Molecular Structure III (Polyatomic Molecules) (New York: Van Nostrand Reinhold) p145
[14] Hartman K O, Hisatsune I C 1966 J. Chem. Phys. 44 1913
Google Scholar
[15] Ovenall D W, Whiffen D H 1961 Mol. Phys. 4 135
Google Scholar
[16] Lahaye J G, Vandenhaute R, Fayt A 1987 J. Mol. Spectrosc. 123 48
Google Scholar
[17] Suzuki I 1975 Bull. Chem. Soc. Jpn. 48 1685
Google Scholar
[18] Bennett J E, Mile B, Thomas A 1967 Trans. Faraday Soc. 63 262
Google Scholar
[19] Yu D, Rauk A, Armstrong D A 1992 J. Phys. Chem. 96 6031
Google Scholar
[20] Gutsev G L, Bartlett R J, Compton R N 1998 J. Chem. Phys. 108 6756
Google Scholar
[21] Barsotti S, Sommerfeld T, Ruf M W, Hotop H 2004 Int. J. Massspectrom. 233 181
[22] Pacansky J, Wahlgren U, Bagus P S 1975 J. Chem. Phys. 62 2740
Google Scholar
[23] Yoshioka Y, Schaefer H F, Jordan K D 1981 J. Chem. Phys. 75 1040
Google Scholar
[24] Surber E, Ananthavel S P, Sanov A 2002 J. Chem. Phys. 116 1920
Google Scholar
[25] Joachim W H, Knowles P J, Knizia G, Manby F R, Schütz M 2012 Wiley Interdiscip. Rev. : Comput. Mol. Sci. 2 242
Google Scholar
[26] Bartlett R J, Watts J D, Kucharski S A, Noga J 1990 Chem. Phys. Lett. 165 513
Google Scholar
[27] Dunning T H, Peterson K A, Wilson A K 2001 J. Chem. Phys. 114 9244
Google Scholar
[28] Fellera D, Peterson K A, Daniel C T 2006 J. Chem. Phys. 124 054107
Google Scholar
[29] Fellera D, Peterson K A 2007 J. Chem. Phys. 126 114105
Google Scholar
[30] Peterson K A, Woon D E, Dunning T H 1994 J. Chem. Phys. 100 7410
Google Scholar
[31] Dunning T H 1989 J. Chem. Phys. 90 1007
Google Scholar
[32] Reiher M, Wolf A 2004 J. Chem. Phys. 121 2037
Google Scholar
[33] Wolf A, Reiher M, Hess B A 2002 J. Chem. Phys. 117 9215
Google Scholar
[34] Peterson K A, Dunning T H 2002 J. Chem. Phys. 117 10548
Google Scholar
[35] Lu T, Chen F W 2012 J. Comput. Chem. 33 580
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 1543
- PDF Downloads: 58
- Cited By: 0
