-
Bubble dynamic behavior and frequency response of encapsulated microbubbles in nonlinear acoustic field is significant in applications such as tumor therapy, thrombolysis, tissue destruction, and ultrasonic lithotripsy. The acoustic cavitation effect includes stable cavitation and transient cavitation. The transformation from stable cavitation to transient cavitation requires a certain threshold, which is also called the transient cavitation threshold. Phospholipid-coated microbubbles are commonly used to enhance acoustic cavitation. However, the acoustic effects of different coating materials are not very clear, especially when considering the nonlinear effects caused by diffraction, scattering, and reflection during ultrasonic propagation. In this paper, the bubble dynamic behaviors and frequency responses of microbubbles under different frequencies, acoustic pressures, and viscoelastic properties of different shell materials are analyzed by coupling the Gilmore-Akulichev-Zener model with the nonlinear model of a lipid envelope and using the KZK equation to simulate the nonlinear acoustic field. At the same time, the influence of the coated material and nonlinear acoustic effects are considered. The bubble dynamic behavior and frequency response under the actually measured sound field are compared with those simulated by the KZK equation. The results show that the nonlinearity will lead the velocity of the microbubble wall to decrease, and when the pressure of ultrasound increases, the main frequency component of the microbubble oscillation increases, making the radial motion of the microbubble more violent. When the frequency changes, the closer the oscillation frequency of the microbubble is to the resonant frequency, the stronger the radial motion of the microbubble is. The coating material can change the harmonic component in the oscillation frequency. When the harmonic is close to the resonance frequency, the radial motion of the microbubble is enhanced. The elasticity of the coated material has almost no effect on the microbubble's frequency response, and the initial viscosity and surface tension of encapsulated microbubble will change the oscillation frequency distribution of encapsulated microbubble. When the initial viscosity of the coated microbubble is smaller, the subharmonic component of the microbubble oscillation increases. When the frequency of the subharmonic is closer to the resonance frequency than the main frequency, the acoustic cavitation effect is significantly enhanced. On the other hand, when the initial surface tension of the encapsulated microbubble increases, the main frequency and subharmonic component of the microbubble oscillation are enhanced, so that the acoustic cavitation effect is also enhanced. Therefore, this study can further elucidate the bubble dynamics of encapsulated microbubbles, stimulated by nonlinear ultrasound, benefiting the frequency response analysis of coated microbubbles under nonlinear acoustic fields.
-
Keywords:
- bubble dynamics /
- nonlinear acoustic field /
- encapsulated microbubble /
- frequency response
[1] Yasui K 2018 Acoustic Cavitation and Bubble Dynamics (Springer
[2] Ashokkumar M 2011 Ultrason. Sonochem. 18 864
Google Scholar
[3] 沈壮志, 林书玉 2011 60 084302
Google Scholar
Shen Z Z, Lin S Y 2011 Acta Phys. Sin. 60 084302
Google Scholar
[4] Gielen B, Jordens J, Janssen J, Pfeiffer H, Wevers M, Thomassen L C J, Braeken L, Van Gerven T 2015 Ultrason. Sonochem. 25 31
Google Scholar
[5] Petit B, Bohren Y, Gaud E, Bussat P, Arditi M, Yan F, Tranquart F, Allémann E 2015 Ultrasound Med. Biol. 41 1402
Google Scholar
[6] Jiménez-Fernández J, Crespo A 2005 Ultrasonics 43 643
Google Scholar
[7] Izadifar Z, Babyn P, Chapman D 2019 J. Med. Biol. Eng. 39 259
Google Scholar
[8] van den Bijgaart R J E, Eikelenboom D C, Hoogenboom M, Fütterer J J, den Brok M H, Adema G J 2017 Cancer Immunol. Immunother. 66 247
Google Scholar
[9] Clark A, Bonilla S, Suo D J, Shapira Y, Averkiou M 2021 Ultrasound Med. Biol. 47 2296
Google Scholar
[10] Suo D J, Guo S, Lin W, Jiang X, Jing Y 2015 Phys. Med. Biol. 60 7403
Google Scholar
[11] Suo D J, Govind B, Gu J, Dayton P A, Jing Y 2019 J. Appl. Phys. 125 084702
Google Scholar
[12] Belzberg M, Mahapatra S, Perdomo-Pantoja A, Chavez F, Morrison K, Xiong K T, Gamo N J, Restaino S, Thakor N, Yazdi Y, Iyer R, Tyler B, Theodore N, Luciano M G, Brem H, Groves M, Cohen A R, Manbachi A 2020 Ultrasonics 108 106210
Google Scholar
[13] Cambronero S, Dupré A, Mastier C, Melodelima D 2023 Ultrasound Med. Biol. 49 212
Google Scholar
[14] Lauterborn W, Kurz T, Geisler R, Schanz D, Lindau O 2007 Ultrason. Sonochem. 14 484
Google Scholar
[15] Lee J, Yasui K, Ashokkumar M, Kentish S E 2018 Cryst. Growth Des. 18 5108
Google Scholar
[16] Pandit A V, Sarvothaman V P, Ranade V V 2021 Ultrason. Sonochem. 77 105677
Google Scholar
[17] Yusof N S M, Babgi B, Alghamdi Y, Aksu M, Madhavan J, Ashokkumar M 2016 Ultrason. Sonochem. 29 568
Google Scholar
[18] Zhang L, Li Z D, Li K, Li H X, Zhao J F 2015 Appl. Therm. Eng. 88 118
Google Scholar
[19] Daghooghi-Mobarakeh H, Daghooghi M, Miner M, Wang L, Wang R, Phelan P E 2022 Therm. Sci. Eng. Prog. 33 101374
Google Scholar
[20] Alehossein H, Qin Z 2007 Int. J. Numer. Methods Eng. 72 780
Google Scholar
[21] Keller J B, Miksis M 1980 J. Acoust. Soc. Am. 68 628
Google Scholar
[22] Doinikov A A 2002 Phys. Fluids 14 1420
Google Scholar
[23] Pelekasis N A, Gaki A, Doinikov A, Tsamopoulos J A 2004 J. Fluid Mech. 500 313
Google Scholar
[24] Yang X, Church C C 2005 Acoust. Res. Lett. Online 6 151
Google Scholar
[25] Suo D J, Govind B, Zhang S, Jing Y 2018 Ultrason. Sonochem. 41 419
Google Scholar
[26] Zilonova E, Solovchuk M, Sheu T W H 2018 Ultrason. Sonochem. 40 900
Google Scholar
[27] Marmottant P, van der Meer S, Emmer M, Versluis M, de Jong N, Hilgenfeldt S, Lohse D 2005 J. Acoust. Soc. Am. 118 3499
Google Scholar
[28] Cui Z, Li D, Xu S, Xu T, Wu S, Bouakaz A, Wan M, Zhang S 2020 Ultrason. Sonochem. 63 104935
Google Scholar
[29] 于洁, 郭霞生, 屠娟, 章东 2015 64 094306
Google Scholar
Yu J, Guo X S, Tu J, Zhang D 2015 Acta Phys. Sin. 64 094306
Google Scholar
[30] 秦对, 邹青钦, 李章勇, 王伟, 万明习, 冯怡 2021 70 154701
Google Scholar
Qin D, Zou Q Q, Li Z Y, Wang W, Wan M X, Feng Y 2021 Acta Phys. Sin. 70 154701
Google Scholar
[31] Kostin I, Panasenko G 2006 CR Mécanique 334 220
Google Scholar
[32] Shevchenko I, Kaltenbacher B 2015 J. Comput. Phys. 302 200
Google Scholar
[33] Bakhtiari-Nejad M, Shahab S 2019 Acoustics 1 14
Google Scholar
[34] Ghalichi F, Behnia S, Mottaghi F, Yahyavi M 2020 Phys. Scr. 95 085215
Google Scholar
[35] Gharloghi S, Gholami M, Haghparast A, Dehlaghi V 2017 Iran. J. Med. Phys. 14 15
Google Scholar
[36] Wang M, Lei Y, Zhou Y 2019 Ultrasonics 91 134
Google Scholar
[37] Li Z, Zou Q, Qin D 2022 Phys. Med. Biol. 67 085017
Google Scholar
[38] Shen Y, Zhang L, Wu Y, Chen W 2021 Ultrason. Sonochem. 73 105535
Google Scholar
-
图 1 线性声场和非线性声场下微泡动力学行为频率响应 (a) 相同正压下的线性超声与非线性超声波形图; (b), (c) 微泡动力学行为的对比; (d) 微泡半径变化的振荡频率响应, 蓝色线条表示驱动声压为KZK方程仿真的非线性声场, 红色线条表示线性声场
Figure 1. Dynamics behavior and frequency response of microbubbles under linear and nonlinear ultrasound fields: (a) Linear and nonlinear ultrasonic waveforms under the same positive pressure; (b), (c) comparison of bubble dynamics behaviors; (d) oscillation frequency response of the microbubble radius change, the blue lines represent the driving sound pressure as the nonlinear ultrasound field simulated by the KZK equation, and the red lines represent the linear ultrasound field.
图 2 (a), (b), (e) 不同声压下非线性超声的微泡动力学行为和频率响应的差异; (c), (d), (f) 不同频率下非线性超声的微泡动力学行为和频率响应差异
Figure 2. (a), (b), (e) Differences in the kinetic behavior and frequency response of microbubbles in nonlinear ultrasound at different acoustic pressures; (c), (d), (f) differences in microbubble kinetic behavior and frequency response of microbubbles in nonlinear ultrasound at different frequencies.
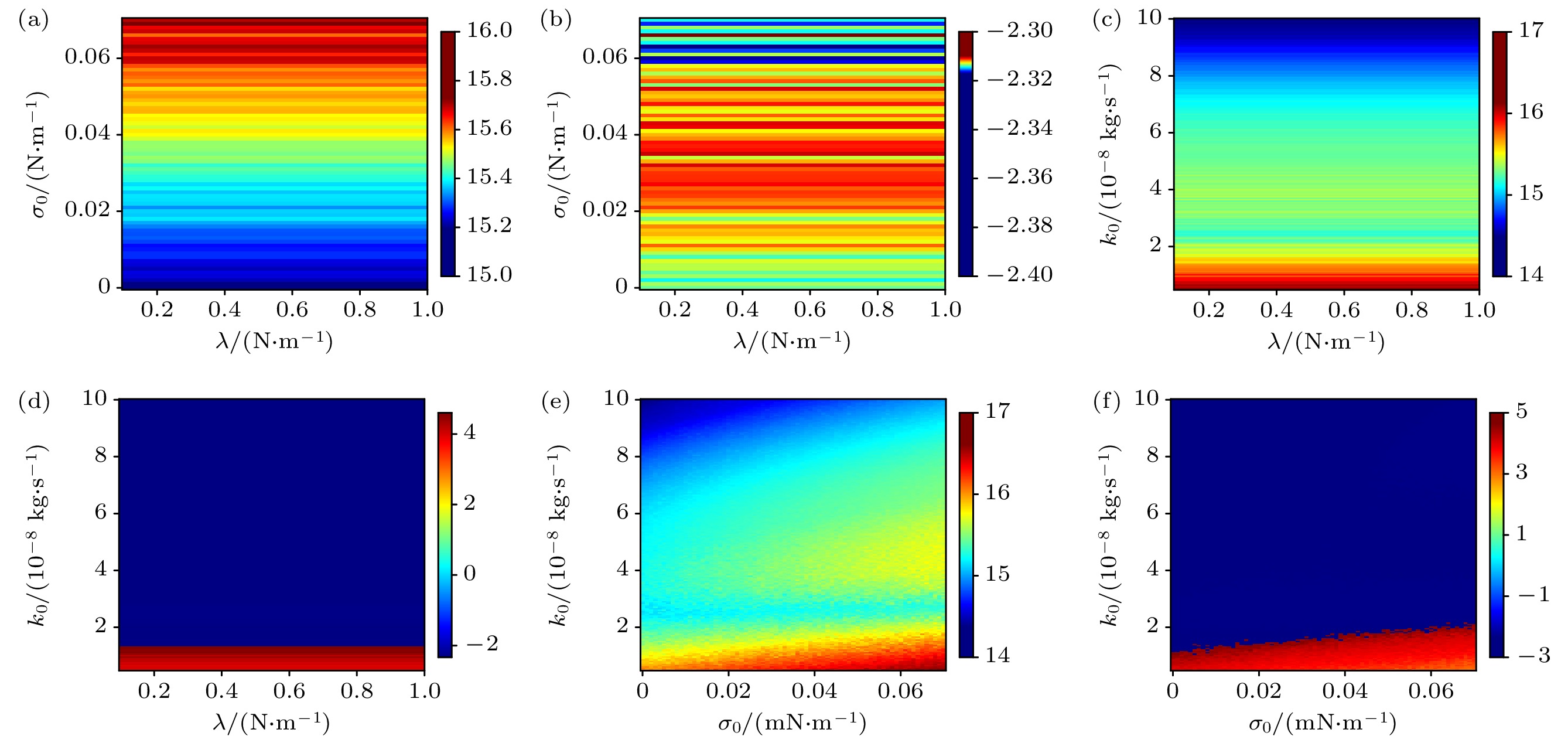
图 3 不同包膜材料对微泡动力学行为和频率响应影响 (a), (b) 包膜微泡的初始表面张力; (c), (d) 包膜的黏性参数
Figure 3. Effects of different coating materials on bubble dynamic behavior and frequency response of encapsulated microbubbles: (a), (b) Initial surface tension of encapsulated microbubbles; (c), (d) viscosity parameters of encapsulated microbubbles.
图 4 不同包膜材料组合对微泡动力学行为和频率响应影响 (a), (c), (e) 颜色表示微泡半径变化; (b), (d), (f) 颜色表示C的变化
Figure 4. Effects of bubble shell on bubble dynamics and frequency response in the nonlinear ultrasound field: (a), (c), (e) Color bar of is the change of radius; (b), (d), (f) color bar is the change of C.
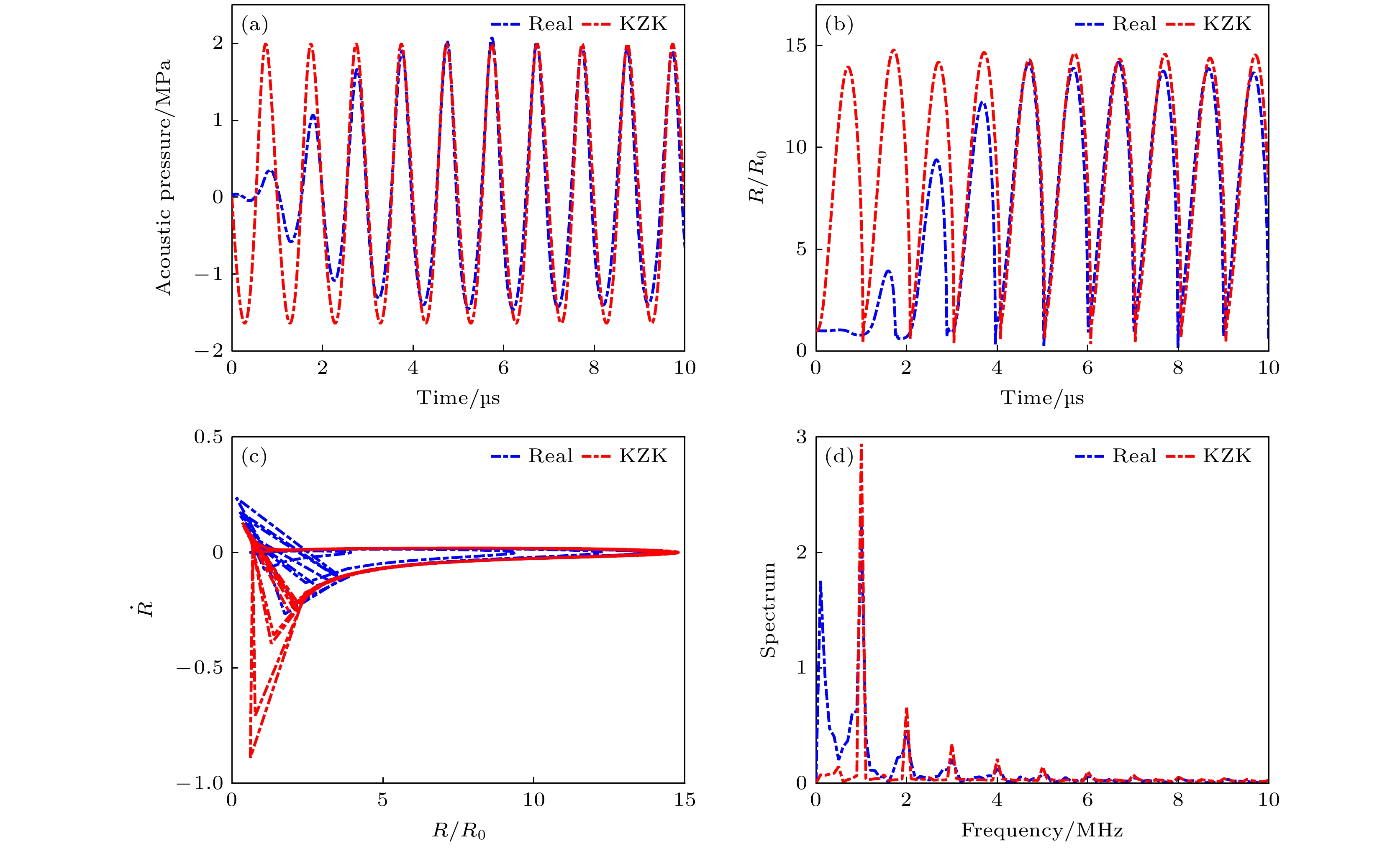
图 5 实际测量值与KZK仿真对比图 (a) 相同正压下实际测量与KZK方程仿真波形图; (b), (c) 微泡动力学行为的对比; (d) 微泡半径变化的振荡频率响应
Figure 5. Actual measured values are compared with the KZK simulation: (a) Actual measurement and KZK equation simulation waveform diagram under the same positive pressure; (b), (c) comparison of the dynamic behavior of microbubbles; (d) oscillation frequency response of the microbubble radius change.
表 1 参数名称和值
Table 1. Name and value of the parameters.
参数 值 静态压力$ {p}_{0} $ 0.1013 MPa 初始半径$ {R}_{0} $ — 多向性系数$ \gamma $ 1.4 Gilmore方程的常数n 7 壳的初始黏性参数$ {k}_{0} $ 5×10–8 kg·s–1 特征时间常数$ \alpha $ 5×10–7 s 包膜微泡的弹性$ \lambda $ 0.44 N/m 介质中的黏性$ \mu $ 0.009 Pa·s 初始表面张力$ {\sigma }_{0} $ 0.01 N/m 组织的表面张力$ {\sigma }_{t} $ 0.068 N/m 组织的松弛时间$ \varphi $ 3×10–9 s 气泡壁的焓变H — 组织密度$ \rho $ 1000 kg/m3 介质的弹性模量G 0 Pa 
DownLoad: CSV
-
[1] Yasui K 2018 Acoustic Cavitation and Bubble Dynamics (Springer
[2] Ashokkumar M 2011 Ultrason. Sonochem. 18 864
Google Scholar
[3] 沈壮志, 林书玉 2011 60 084302
Google Scholar
Shen Z Z, Lin S Y 2011 Acta Phys. Sin. 60 084302
Google Scholar
[4] Gielen B, Jordens J, Janssen J, Pfeiffer H, Wevers M, Thomassen L C J, Braeken L, Van Gerven T 2015 Ultrason. Sonochem. 25 31
Google Scholar
[5] Petit B, Bohren Y, Gaud E, Bussat P, Arditi M, Yan F, Tranquart F, Allémann E 2015 Ultrasound Med. Biol. 41 1402
Google Scholar
[6] Jiménez-Fernández J, Crespo A 2005 Ultrasonics 43 643
Google Scholar
[7] Izadifar Z, Babyn P, Chapman D 2019 J. Med. Biol. Eng. 39 259
Google Scholar
[8] van den Bijgaart R J E, Eikelenboom D C, Hoogenboom M, Fütterer J J, den Brok M H, Adema G J 2017 Cancer Immunol. Immunother. 66 247
Google Scholar
[9] Clark A, Bonilla S, Suo D J, Shapira Y, Averkiou M 2021 Ultrasound Med. Biol. 47 2296
Google Scholar
[10] Suo D J, Guo S, Lin W, Jiang X, Jing Y 2015 Phys. Med. Biol. 60 7403
Google Scholar
[11] Suo D J, Govind B, Gu J, Dayton P A, Jing Y 2019 J. Appl. Phys. 125 084702
Google Scholar
[12] Belzberg M, Mahapatra S, Perdomo-Pantoja A, Chavez F, Morrison K, Xiong K T, Gamo N J, Restaino S, Thakor N, Yazdi Y, Iyer R, Tyler B, Theodore N, Luciano M G, Brem H, Groves M, Cohen A R, Manbachi A 2020 Ultrasonics 108 106210
Google Scholar
[13] Cambronero S, Dupré A, Mastier C, Melodelima D 2023 Ultrasound Med. Biol. 49 212
Google Scholar
[14] Lauterborn W, Kurz T, Geisler R, Schanz D, Lindau O 2007 Ultrason. Sonochem. 14 484
Google Scholar
[15] Lee J, Yasui K, Ashokkumar M, Kentish S E 2018 Cryst. Growth Des. 18 5108
Google Scholar
[16] Pandit A V, Sarvothaman V P, Ranade V V 2021 Ultrason. Sonochem. 77 105677
Google Scholar
[17] Yusof N S M, Babgi B, Alghamdi Y, Aksu M, Madhavan J, Ashokkumar M 2016 Ultrason. Sonochem. 29 568
Google Scholar
[18] Zhang L, Li Z D, Li K, Li H X, Zhao J F 2015 Appl. Therm. Eng. 88 118
Google Scholar
[19] Daghooghi-Mobarakeh H, Daghooghi M, Miner M, Wang L, Wang R, Phelan P E 2022 Therm. Sci. Eng. Prog. 33 101374
Google Scholar
[20] Alehossein H, Qin Z 2007 Int. J. Numer. Methods Eng. 72 780
Google Scholar
[21] Keller J B, Miksis M 1980 J. Acoust. Soc. Am. 68 628
Google Scholar
[22] Doinikov A A 2002 Phys. Fluids 14 1420
Google Scholar
[23] Pelekasis N A, Gaki A, Doinikov A, Tsamopoulos J A 2004 J. Fluid Mech. 500 313
Google Scholar
[24] Yang X, Church C C 2005 Acoust. Res. Lett. Online 6 151
Google Scholar
[25] Suo D J, Govind B, Zhang S, Jing Y 2018 Ultrason. Sonochem. 41 419
Google Scholar
[26] Zilonova E, Solovchuk M, Sheu T W H 2018 Ultrason. Sonochem. 40 900
Google Scholar
[27] Marmottant P, van der Meer S, Emmer M, Versluis M, de Jong N, Hilgenfeldt S, Lohse D 2005 J. Acoust. Soc. Am. 118 3499
Google Scholar
[28] Cui Z, Li D, Xu S, Xu T, Wu S, Bouakaz A, Wan M, Zhang S 2020 Ultrason. Sonochem. 63 104935
Google Scholar
[29] 于洁, 郭霞生, 屠娟, 章东 2015 64 094306
Google Scholar
Yu J, Guo X S, Tu J, Zhang D 2015 Acta Phys. Sin. 64 094306
Google Scholar
[30] 秦对, 邹青钦, 李章勇, 王伟, 万明习, 冯怡 2021 70 154701
Google Scholar
Qin D, Zou Q Q, Li Z Y, Wang W, Wan M X, Feng Y 2021 Acta Phys. Sin. 70 154701
Google Scholar
[31] Kostin I, Panasenko G 2006 CR Mécanique 334 220
Google Scholar
[32] Shevchenko I, Kaltenbacher B 2015 J. Comput. Phys. 302 200
Google Scholar
[33] Bakhtiari-Nejad M, Shahab S 2019 Acoustics 1 14
Google Scholar
[34] Ghalichi F, Behnia S, Mottaghi F, Yahyavi M 2020 Phys. Scr. 95 085215
Google Scholar
[35] Gharloghi S, Gholami M, Haghparast A, Dehlaghi V 2017 Iran. J. Med. Phys. 14 15
Google Scholar
[36] Wang M, Lei Y, Zhou Y 2019 Ultrasonics 91 134
Google Scholar
[37] Li Z, Zou Q, Qin D 2022 Phys. Med. Biol. 67 085017
Google Scholar
[38] Shen Y, Zhang L, Wu Y, Chen W 2021 Ultrason. Sonochem. 73 105535
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 1912
- PDF Downloads: 74
- Cited By: 0
