-
Currently, the measurement and prediction of the electrical transport performance of thermoelectric double-layer membrane is often based on the theory of parallel model. However, the conditions under which the parallel model can be used lack theoretical and experimental support and validation. In this work, the Seebeck coefficients of Cu/Si and Ag/Si bilayers under applied temperature difference are obtained by using finite element theory simulations with the help of COMSOL Multiphysics software and compared with the results from the parallel model. Whether the ends of the bilayer plated with a metal Pt layer, and the insertion of a high-resistance/low-resistance/insulation interface between the bilayers affect the Seebeck coefficient measurements of the bilayer are investigated. It is found that when there is no Pt at the hot end or cold end, the potentials on the Si side and Cu side at the high-resistance and electrically insulating interfaces are uniformly distributed along the direction of the temperature gradient, respectively, and the measured Seebeck coefficients are the same as the values of the materials’ own, respectively, and the thermal potential on the Cu side at the low-resistance interface varies uniformly with the probe spacing L, while the thermal potential on the Si side shows a non-uniform variation. With Pt, the thermal potentials on the Cu side and Si side are uniformly distributed along the direction of the temperature gradient, and the measured values on both Si side and Cu side are the same as the Cu Seebeck coefficients, regardless of the insulating/high-resistance/low-resistance interface. The Si/Ag and Bi/Ag bilayers are investigated experimentally. In the absence of Pt, the absolute value of the Seebeck coefficient on the Si side of Si/Ag bilayer decreases with temperature decreasing, but the absolute value of the Seebeck coefficient on the Ag side increases with temperature decreasing. In the presence of Pt, the Seebeck coefficients on both sides of the Bi/Ag bilayer membrane are equal.
-
Keywords:
- double-layer thermoelectric film /
- Seebeck coefficient /
- double layer parallel model /
- COMSOL Multiphysics
[1] 陈立东, 刘睿恒, 史讯 2017 热电材料与器件 (北京: 科学出版社) 第1页
Chen L D, Liu R H, Shi X 2017 Thermoelectric Materials and Devices (Beijing: Science Press) p1
[2] Mizue M, Masashi M, Kimihiro O 2013 J. Micromech. Microeng. 23 115016
Google Scholar
[3] Nouredine O, Alain P, Abdelkhalek K, Khalid H 2023 Eur. Phys. J. Appl. Phys. 98 29
Google Scholar
[4] Ihtesham C, Ravi P, Kelly L, Gregory C, Sridhar N, Ravi M, David K, Randall A, Rama V 2009 Nat. Nanotechnol. 4 235
Google Scholar
[5] Yang C, Souchay D, Knei M, et al. 2017 Nat. Commun. 8 16076
Google Scholar
[6] Pilaipon N, Rachsak S, Mati H, Aparporn S 2017 J. Electron. Mater. 4 66444
Google Scholar
[7] Yordanov P, Wochner P, Ibrahimkutty S, Dietl C, Wrobel F, Felici R, Gregori G, Maier J, Keimer B, Habermeier H U 2017 Appl. Phys. Lett. 110 253101
Google Scholar
[8] Gromova D G, Shterna Y I, Rogacheva M S, Shulyat’eva A S, Kirilenkoa E P, Shterna M Y, Fedorovb V A, Mikhailovaa M S 2016 Inorg. Mater. 52 1132
Google Scholar
[9] Hinterleitner B, Knapp I, Poneder M, et al. 2019 Nature 576 85
Google Scholar
[10] Masaaki I, Hironori A, Daisuke T, Jiro K 2019 Electr. Eng. Jpn. 208 10
Google Scholar
[11] Ju H, Kim J 2019 ACS Appl. Mater. Interfaces 11 35354
Google Scholar
[12] Liu S Y, Peng S J, Ma J, Li G J, Qin X S, Li M M, Wang Q 2017 Superlattice. Microst. 104 282
Google Scholar
[13] Tani J I, Ishikawa H 2023 Mater. Lett. 331 133460
Google Scholar
[14] Tian K, Tiwar A 2019 Sci. Rep. 9 3133
Google Scholar
[15] Usop R, Hasnan M M I M, Mohamad M, Ahmad M K, Said S M, Salleh F 2022 Micromachines. Basel. 13 2169
Google Scholar
[16] Stevens D L, Ortiz A, Cho C, Gamage G A, Ren Z F, Grunlan J C 2021 Appl. Phys. Lett. 118 151904
Google Scholar
[17] Sumino M, Harada K, Ikeda M, Tanaka S, Miyazaki K, Adachi C 2011 Appl. Phys. Lett. 118 093308
Google Scholar
[18] Nordheim V L, Gorter C J 1935 Physics 2 383
Google Scholar
[19] Ho T L, Ding K, Lyapunov N, Suen C H, Wong L W, Zhao J, Yang M, Zhou X, Dai J Y 2022 Nanomaterials. Basel. 12 2128
Google Scholar
[20] Hinterleitner B, Knapp I, Poneder M, et al. 2008 Appl. Phys. Lett. 92 191911
Google Scholar
[21] Bhogra A, Masarrat A, Hasina D, Meena R, Kumar A, Som T, Dong C L, Chen C L, Kandasami A 2021 Mater. Lett. 282 128880
Google Scholar
[22] Koga T, Cronin S B, Dresselhaus M S, Liu J L, Wang K L 2000 Appl. Phys. Lett. 77 1490
Google Scholar
[23] Heinze S, Habermeier H U, Cristiani G, Canosa S B, Tacon M L, Keimer B 2012 Appl. Phys. Lett. 101 131603
Google Scholar
[24] Meng J H, Wu H C, Gao D Y, Zhang K, Gui L, Yan W M 2020 Energy 217 119360
[25] Chen L, Lee J 2015 Appl. Energ. 150 138
Google Scholar
-
图 1 (a)金属/半导体双层膜结构; (b)根据并联模型给出的测试示意图
Figure 1. (a) Bilayered thin film with metal/semiconductor structure; (b) measurement schematic given based on the parallel mode.
图 2 (a)低温电输运测量原理示意图; (b) CTA-3测量原理示意图
Figure 2. (a) Schematic diagram of the measurement principle of low-temperature electrical transport; (b) schematic diagram of CTA-3 measurement principle.
图 3 双层膜两端无镀Pt(a)和有镀Pt(b)的Seebeck系数测量示意图
Figure 3. Measurement schematic of Seebeck coefficient without Pt (a) and with Pt (b) plated at both ends of bilayered thin films.
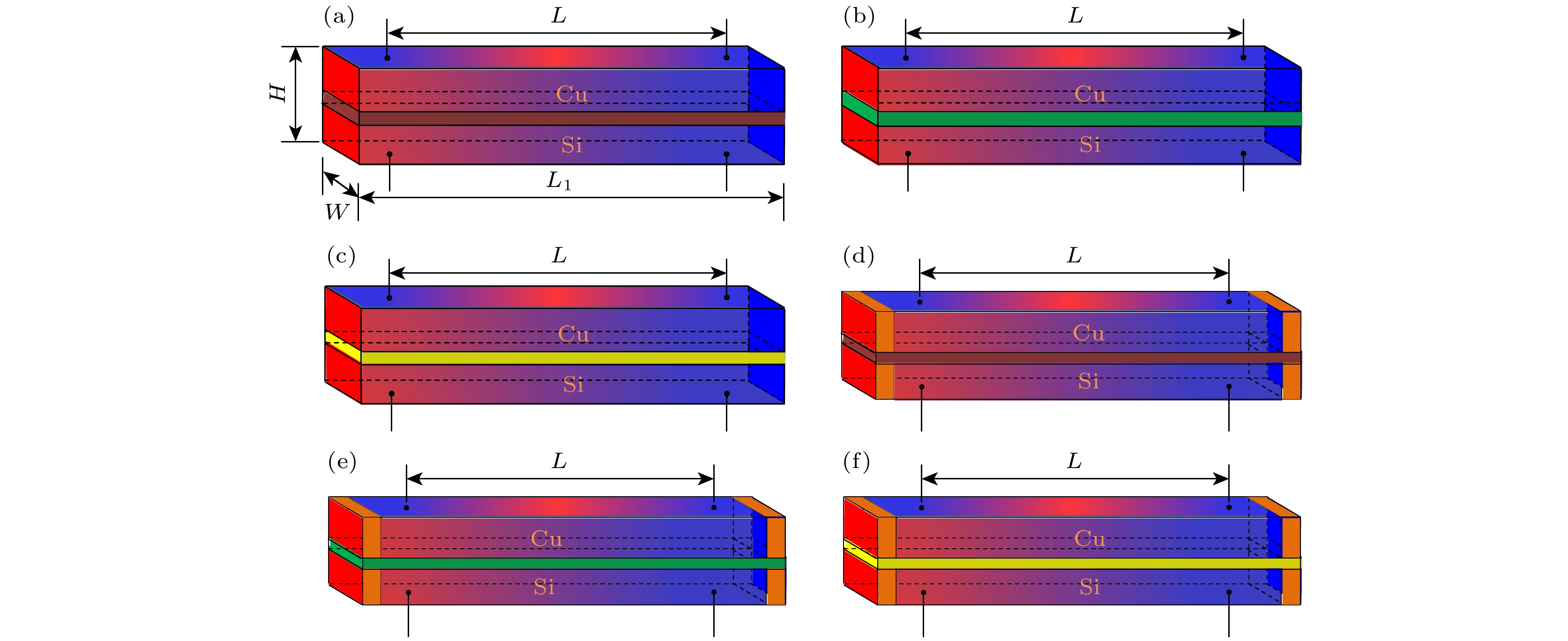
图 4 双层膜热电模型 (a)无Pt高阻界面; (b)无Pt低阻界面; (c)无Pt电绝缘界面; (d)有Pt高阻界面; (e)有Pt低阻界面; (f)有Pt电绝缘界面
Figure 4. Two-layer thermoelectric model: (a) Without Pt high resistance interface; (b) Pt low resistance interface; (c) Pt electrical insulation interface; (d) Pt high resistance interface; (e) Pt low resistance interface; (f) Pt electrical insulation interface.
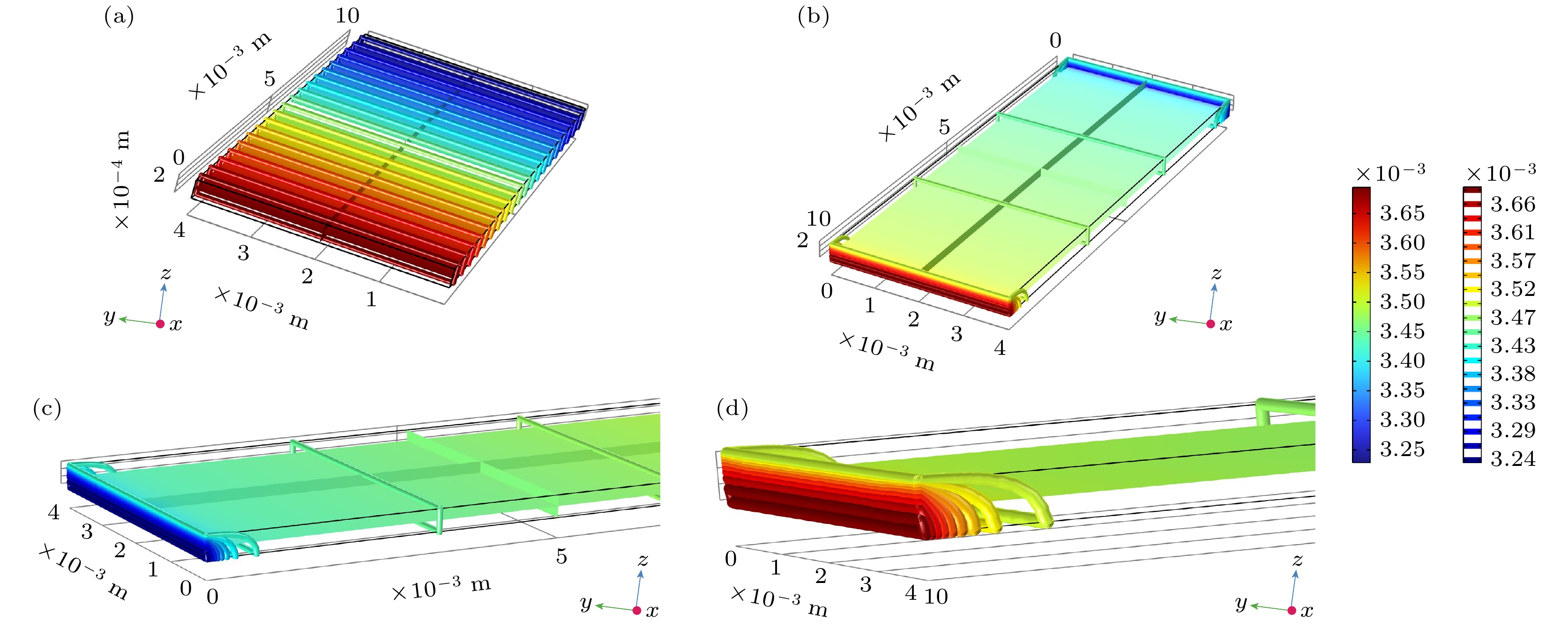
图 5 (a)有Pt模型模型热电势分布图; (b)无Pt模型模型热电势分布图; (c)无Pt模型热端热电势分布图; (d)无Pt模型冷端热电势分布图
Figure 5. (a) Thermoelectric potential distribution diagram with Pt model; (b) thermoelectric potential distribution diagram without Pt model; (c) thermoelectric potential distribution diagram at the hot end of the Pt model; (d) thermoelectric potential distribution diagram of the cold end of the Pt-free model.
图 6 (a)有Pt模型与无Pt模型热电势分布曲线; (b)有Pt模型和无Pt模型Si和Cu侧不同位置测量的Seebeck系数及根据并联模型验证公式得到的Cu/Si双层膜的Seebeck系数理论值
Figure 6. (a) Thermoelectric potential distribution curves with and without Pt model; (b) Seebeck coefficients measured at different positions on Si and Cu side with and without Pt model and their parallel verification formulas.
图 7 (a)无Pt时高阻或电绝缘界面; (b)无Pt低阻界面双层热电模型热电势分布图
Figure 7. (a) High resistance or electrical insulation interface without Pt; (b) thermoelectric potential distribution diagram of double-layer thermoelectric model without Pt low resistance interface.
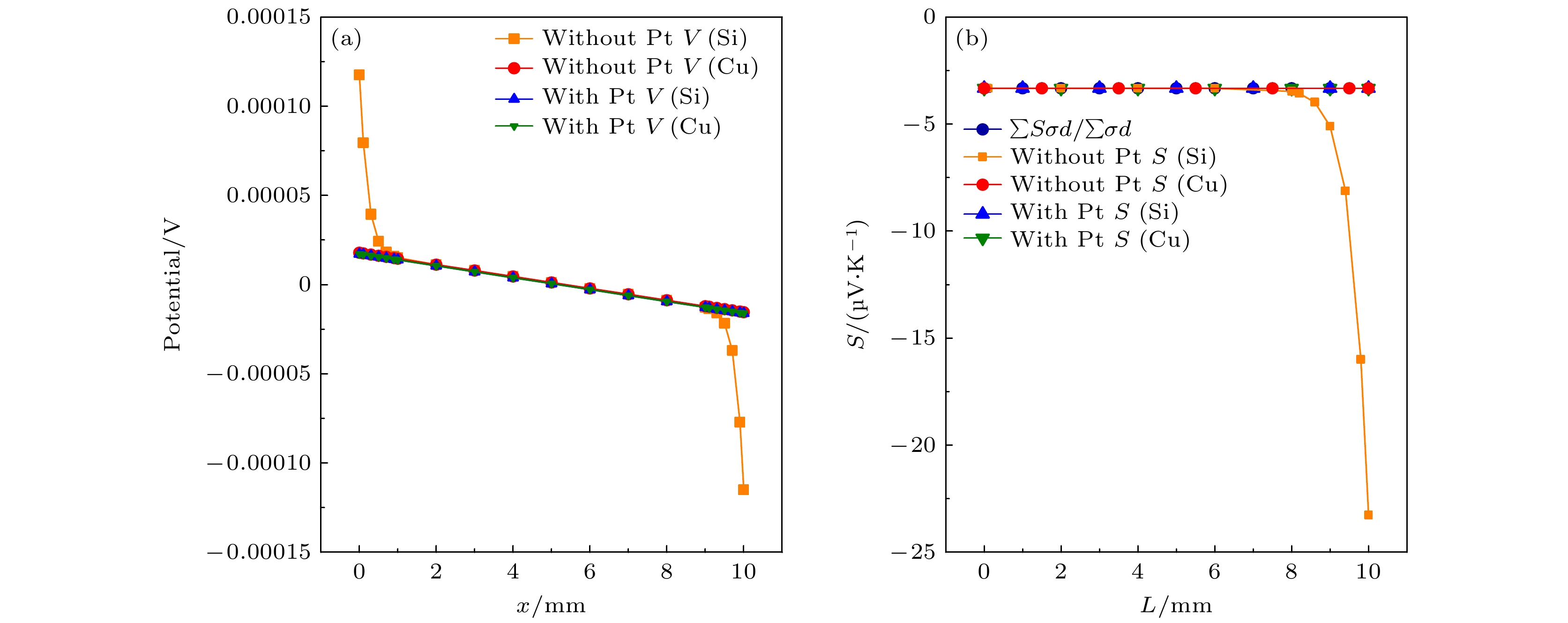
图 8 (a)无Pt高阻或电绝缘界面热电势分布曲线; (b) 无Pt低阻界面的热电势分布曲线; (c)无Pt高阻或电绝缘界面双层热电模型不同位置的Seebeck系数; (d)无Pt低阻界面双层热电模型不同位置的Seebeck系数
Figure 8. (a) Thermoelectric potential distribution curve at the interface without Pt high resistance or electrical insulation; (b) thermoelectric potential distribution curve without PT-low resistance interface; (c) Seebeck coefficients at different locations of double-layer thermoelectric models without Pt high resistance or electrically insulated interfaces; (d) Seebeck coefficients at different positions of a two-layer thermoelectric model without Pt low resistance interface.
图 9 (a)有Pt低阻或高阻界面; (b)有Pt电绝缘界面双层热电模型热电势分布图
Figure 9. (a) Interface with low or high Pt resistance; (b) thermoelectric potential distribution diagram of double-layer thermoelectric model with Pt electrical insulation interface.
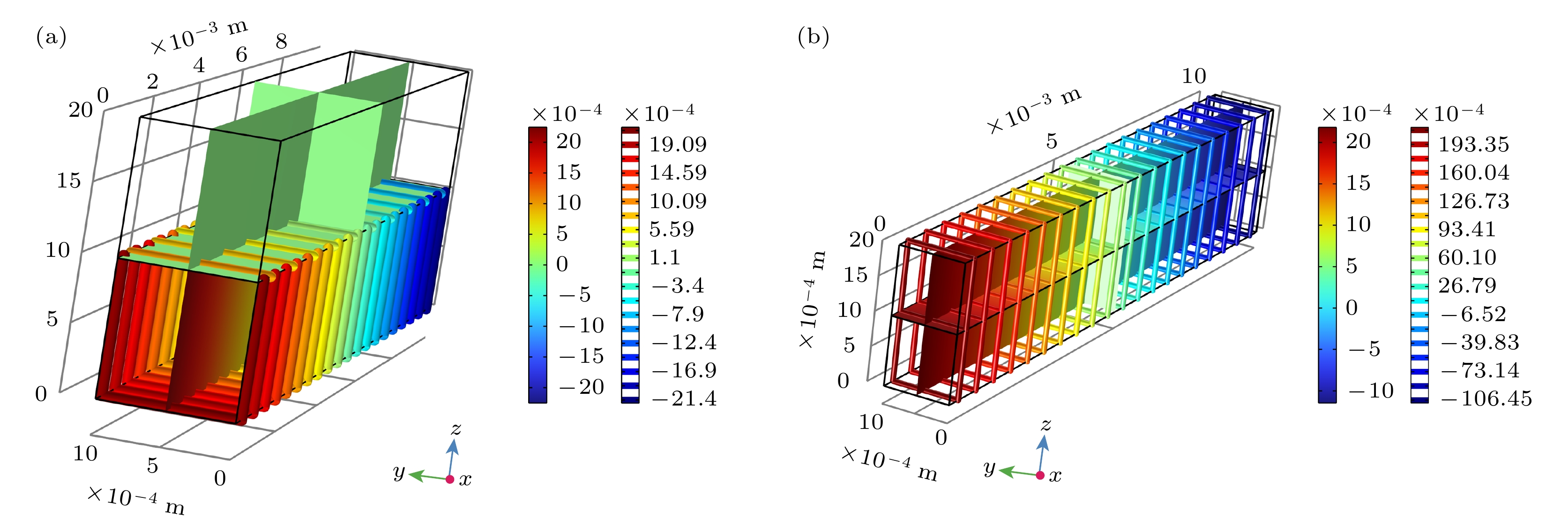
图 10 (a)有Pt高阻、低阻界面双层热电模型Si侧、界面、Cu侧热电势分布曲线; (b) 有Pt高阻或低阻界面双层热电模型不同位置的Seebeck系数; (c)有Pt电绝缘界面双层热电模型Si侧、界面、Cu侧热电势分布曲线; (d)有Pt电绝缘界面不同位置的Seebeck系数
Figure 10. (a) Thermoelectric potential distribution curves on Si side, interface and Cu side of the double-layer thermoelectric model with Pt high resistance and low resistance interface; (b) Seebeck coefficients at different locations of double-layer thermoelectric models with Pt high or low resistance interfaces; (c) thermoelectric potential distribution curves of Si side, interface and Cu side of double-layer thermoelectric model with Pt electrical insulation interface; (d) Seebeck coefficient with Pt electrical insulation interface at different positions.
图 11 (a)不同温度下Si/Ag双层膜Si侧、Ag侧的Seebeck系数; (b) 300 K有Pt不同镀银厚度下Bi/Ag双层膜Bi侧、Ag侧的Seebeck系数
Figure 11. (a) Seebeck coefficients of Si/Ag bilayer films on Si side and Ag side at different temperatures; (b) Seebeck coefficient of Bi/Ag bilayer film on Bi side and Ag side at different silver plating thickness of Pt at 300 K.
表 1 室温下双层膜正面及反面Seebeck系数测量结果
Table 1. Measurement results of Seebeck coefficient on front and back of the bilayered thin films at room temperature.
n-Si Ag/n-Si SI-Si Ag/SI-Si Cu/n-Si Cu/n-Si 正面/(µV·K–1) –430 –1.25 –3.33×104 –2.78×10–1 –7.83 –8.02 反面/(µV·K–1) –416 –218.75 –3.24×104 –3.89×104 –401 –415 
DownLoad: CSV
表 2 Si, Cu, Ag, Bi的材料参数
Table 2. Material parameters of Si, Cu, Ag and Bi.
名称 Si Cu Ag Bi 相对介电常数(1) 11.7 1 — — 导热系数/(W·m–1·K–1) 131 400 — — 密度/(kg·m–3) 2329 8700 — — 常压热容/(J·kg–1·K–1) 700 385 — — 电导率/(S·m–1) 2.52×10–4 5.998×107 1.01×107 5.77×105 Seebeck系数/(V·K–1) –0.45×10–3 –3.33×10–6 5.81×10–6 –6.36×10–5
DownLoad: CSV
-
[1] 陈立东, 刘睿恒, 史讯 2017 热电材料与器件 (北京: 科学出版社) 第1页
Chen L D, Liu R H, Shi X 2017 Thermoelectric Materials and Devices (Beijing: Science Press) p1
[2] Mizue M, Masashi M, Kimihiro O 2013 J. Micromech. Microeng. 23 115016
Google Scholar
[3] Nouredine O, Alain P, Abdelkhalek K, Khalid H 2023 Eur. Phys. J. Appl. Phys. 98 29
Google Scholar
[4] Ihtesham C, Ravi P, Kelly L, Gregory C, Sridhar N, Ravi M, David K, Randall A, Rama V 2009 Nat. Nanotechnol. 4 235
Google Scholar
[5] Yang C, Souchay D, Knei M, et al. 2017 Nat. Commun. 8 16076
Google Scholar
[6] Pilaipon N, Rachsak S, Mati H, Aparporn S 2017 J. Electron. Mater. 4 66444
Google Scholar
[7] Yordanov P, Wochner P, Ibrahimkutty S, Dietl C, Wrobel F, Felici R, Gregori G, Maier J, Keimer B, Habermeier H U 2017 Appl. Phys. Lett. 110 253101
Google Scholar
[8] Gromova D G, Shterna Y I, Rogacheva M S, Shulyat’eva A S, Kirilenkoa E P, Shterna M Y, Fedorovb V A, Mikhailovaa M S 2016 Inorg. Mater. 52 1132
Google Scholar
[9] Hinterleitner B, Knapp I, Poneder M, et al. 2019 Nature 576 85
Google Scholar
[10] Masaaki I, Hironori A, Daisuke T, Jiro K 2019 Electr. Eng. Jpn. 208 10
Google Scholar
[11] Ju H, Kim J 2019 ACS Appl. Mater. Interfaces 11 35354
Google Scholar
[12] Liu S Y, Peng S J, Ma J, Li G J, Qin X S, Li M M, Wang Q 2017 Superlattice. Microst. 104 282
Google Scholar
[13] Tani J I, Ishikawa H 2023 Mater. Lett. 331 133460
Google Scholar
[14] Tian K, Tiwar A 2019 Sci. Rep. 9 3133
Google Scholar
[15] Usop R, Hasnan M M I M, Mohamad M, Ahmad M K, Said S M, Salleh F 2022 Micromachines. Basel. 13 2169
Google Scholar
[16] Stevens D L, Ortiz A, Cho C, Gamage G A, Ren Z F, Grunlan J C 2021 Appl. Phys. Lett. 118 151904
Google Scholar
[17] Sumino M, Harada K, Ikeda M, Tanaka S, Miyazaki K, Adachi C 2011 Appl. Phys. Lett. 118 093308
Google Scholar
[18] Nordheim V L, Gorter C J 1935 Physics 2 383
Google Scholar
[19] Ho T L, Ding K, Lyapunov N, Suen C H, Wong L W, Zhao J, Yang M, Zhou X, Dai J Y 2022 Nanomaterials. Basel. 12 2128
Google Scholar
[20] Hinterleitner B, Knapp I, Poneder M, et al. 2008 Appl. Phys. Lett. 92 191911
Google Scholar
[21] Bhogra A, Masarrat A, Hasina D, Meena R, Kumar A, Som T, Dong C L, Chen C L, Kandasami A 2021 Mater. Lett. 282 128880
Google Scholar
[22] Koga T, Cronin S B, Dresselhaus M S, Liu J L, Wang K L 2000 Appl. Phys. Lett. 77 1490
Google Scholar
[23] Heinze S, Habermeier H U, Cristiani G, Canosa S B, Tacon M L, Keimer B 2012 Appl. Phys. Lett. 101 131603
Google Scholar
[24] Meng J H, Wu H C, Gao D Y, Zhang K, Gui L, Yan W M 2020 Energy 217 119360
[25] Chen L, Lee J 2015 Appl. Energ. 150 138
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2188
- PDF Downloads: 54
- Cited By: 0
