-
We investigate the dynamics of the plane wave state in one-dimensional spin-tensor-momentum coupled Bose-Einstein condensate. By using the Gaussian variational approximation, we first derive the equations of motion for the variational parameters, including the center-of-mass coordinate, momentum, amplitude, width, chirp, and relative phase. These variational parameters are coupled together nonlinearly by the spin-tensor-momentum coupling, Raman coupling, and the spin-dependent atomic interaction. By minimizing the energy with respect to the variational parameters, we find that the ground state is a biaxial nematic state, the momentum of the ground state decreases monotonically with the increase of the strength of the Raman coupling, and the parity of real part of the ground-state wave function is opposite to that of the imaginary part. The linear stability analysis shows that the ground state is dynamically stable under a perturbation, and exhibits three different oscillation excitation modes, the frequencies of which are related to the strength of the Raman coupling, the aspect ratio of the harmonic trap, and the strength of the atomic interaction. By solving the equations of motion for the variational parameters, we find that the system displays periodical oscillation in the dynamical evolution. These variational results are also confirmed by the direct numerical simulations of the Gross-Pitaevskii equations, and these findings reveal the unique properties given by the spin-tensor-momentum coupling.
[1] Qi X L, Zhang S C 2010 Phys. Today 63 33
Google Scholar
[2] Lin Y J, Jiménez-GarcÍa K, Spielman I B 2011 Nature 471 83
Google Scholar
[3] Zhang J Y, Ji S C, Chen Z, Zhang L, Du Z D, Yan B, Pan G S, Zhao B, Deng Y J, Zhai H, Chen S, Pan J W 2012 Phys. Rev. Lett. 109 115301
Google Scholar
[4] Wang P, Yu Z Q, Fu Z, Miao J, Huang L, Chai S, Zhai H, Zhang J 2012 Phys. Rev. Lett. 109 095301
Google Scholar
[5] Cheuk L W, Sommer A T, Hadzibabic Z, Yefsah T, Bakr W S, Zwierlein M W 2012 Phys. Rev. Lett. 109 095302
Google Scholar
[6] Chen H R, Lin K Y, Chen P K, Chiu N C, Wang J B, Chen C A, Huang P P, Yip S K, Kawaguchi Y, Lin Y J 2018 Phys. Rev. Lett. 121 113204
Google Scholar
[7] Chen P K, Liu L R, Tsai M J, Chiu N C, Kawaguchi Y, Yip S K, Chang M S, Lin Y J 2018 Phys. Rev. Lett. 121 250401
Google Scholar
[8] Zhang D, Gao T, Zou P, Kong L, Li R, Shen X, Chen X L, Peng S G, Zhan M, Pu H, Jiang K 2019 Phys. Rev. Lett. 122 110402
Google Scholar
[9] Kawaguchi Y, Ueda M 2012 Phys. Rep. 520 253
Google Scholar
[10] Li D, Huang L, Peng P, Bian G, Wang P, Meng Z, Chen L, Zhang J 2020 Phys. Rev. A 102 013309
Google Scholar
[11] Luo X W, Sun K, Zhang C 2017 Phys. Rev. Lett. 119 193001
Google Scholar
[12] Chen L, Zhang Y, Pu H 2020 Phys. Rev. Lett. 125 195303
Google Scholar
[13] Hu H, Hou J, Zhang F, Zhang C 2018 Phys. Rev. Lett. 120 240401
Google Scholar
[14] Lei Z, Deng Y, Lee C 2022 Phys. Rev. Res. 4 033008
Google Scholar
[15] Sun J, Chen Y, Chen X, Zhang Y 2020 Phys. Rev. A 101 053621
Google Scholar
[16] Liu Y, Liu Y K 2021 Mod. Phys. Lett. B 35 2150232
Google Scholar
[17] Campbell D L, Price R M, Putra A, Valdes-Curiel A, Trypogeorgos D, Spielman I B 2016 Nat. Commun. 7 10897
Google Scholar
[18] Xue M, Li X, Ye W, Chen J J, Xu Z F, You L 2022 Phys. Rev. A 106 033708
Google Scholar
[19] Masson S J, Barrett M D, Parkins S 2017 Phys. Rev. Lett. 119 213601
Google Scholar
[20] Davis E J, Bentsen G, Homeier L, Li T, Schleier-Smith M H 2019 Phys. Rev. Lett. 122 010405
Google Scholar
[21] Periwal A, Cooper E S, Kunkel P, Wienand J F, Davis E J, Schleier-Smith M 2021 Nature 600 630
Google Scholar
[22] Diener R B, Ho T L 2006 Phys. Rev. Lett. 96 190405
Google Scholar
[23] Mueller E J 2004 Phys. Rev. A 69 033606
Google Scholar
[24] Natu S S, Li X, Cole W S 2015 Phys. Rev. A 91 023608
Google Scholar
[25] Malomed B A 2006 Soliton Management in Periodic Systems (Vol. 1) (Berlin: Springer) pp27−29
[26] Liu W, Cai Y 2021 SIAM J. Sci. Comput. 43 B219
Google Scholar
[27] Williams J, Walser R, Cooper J, Cornell E, Holland M 2000 Phys. Rev. A 61 033612
Google Scholar
[28] Öhberg P, Stenholm S 1999 Phys. Rev. A 59 3890
Google Scholar
[29] Lee C, Shi L, Gao K 2004 Phys. Rev. A 69 033611
Google Scholar
[30] Bao W, Cai Y 2018 Commun. Comput. Phys. 24 899
Google Scholar
-
图 1
$ \delta_\text{r}/E_\text{r} = 0 $ (a)和–2 (b)时, 单粒子能量色散曲线, 其中$ \varOmega_\text{r}/E_\text{r} = 2 $ Figure 1. Single-particle energy dispersion curves for
$ \delta_\text{r}/E_\text{r} = 0 $ (a) and –2 (b), respectively, where$ \varOmega_\text{r}/E_\text{r} = 2 $ 
图 2 (a), (b)参数
$ \theta_\ast $ ,$ k_\ast $ 及向列矩阵$ {\boldsymbol{{\cal{N}}}} $ 的本征值$ \lambda_{1} $ ,$ \lambda_2 $ 和$ \lambda_3 $ 随$ \varOmega/k_\text{R}^2 $ 的变化, 其他参数的取值为$ g_\text{n}/k_\text{R} = 1 $ ,$ g_\text{s}/k_\text{R} = 0.1 $ 和$ \gamma/k_\text{R}^2 = 0.2 $ ; (c), (d)基态波函数的实部和虚部随空间坐标的变化, 其他参数的取值为$ g_\text{n} = 1 $ ,$ g_\text{s} = 0.1 $ ,$ \gamma = 0.2 $ ,$ \varOmega=k_\text{R} = 1 $ ; 图中的线代表GP方程的数值解, 圆圈代表变分计算结果Figure 2. (a), (b)
$ \theta_\ast $ ,$ k_\ast $ ,$ \lambda_1 $ ,$ \lambda_2 $ and$ \lambda_{3} $ as a function of$ \varOmega/k_\text{R}^2 $ , where the other parameters are$ g_\text{n}/k_\text{R} = 1 $ ,$ g_\text{s}/k_\text{R} = 0.1 $ and$ \gamma/k_\text{R}^2 = 0.2 $ ; (c), (d) the real and imaginary parts of the wave functions in ground state for$ g_\text{n} = 1 $ ,$ g_\text{s} = 0.1 $ ,$ \gamma = 0.2 $ and$ \varOmega=k_\text{R} = 1 $ . The lines and circles are the results given by GP simulation and the variational method, respectively
图 3 激发频率ω随
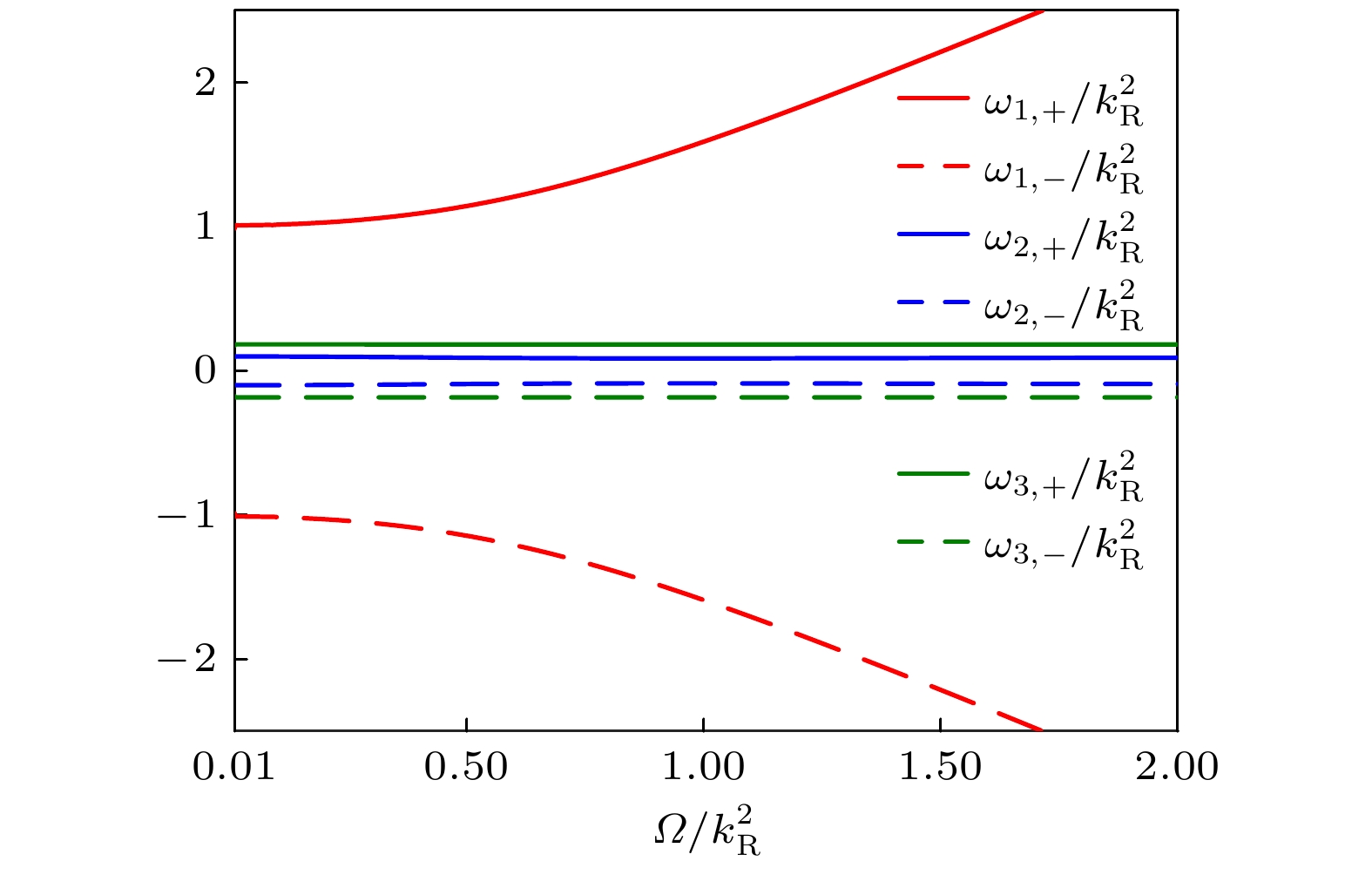
$ \varOmega/k_\text{R}^2 $ 的变化, 其中$ g_\text{n}/k_\text{R} = 1 $ ,$ g_\text{s}/k_\text{R} = $ $ 0.1 $ 及$ \gamma/k_\text{R}^2 = 0.1 $ Figure 3. Excitation frequency as the function of
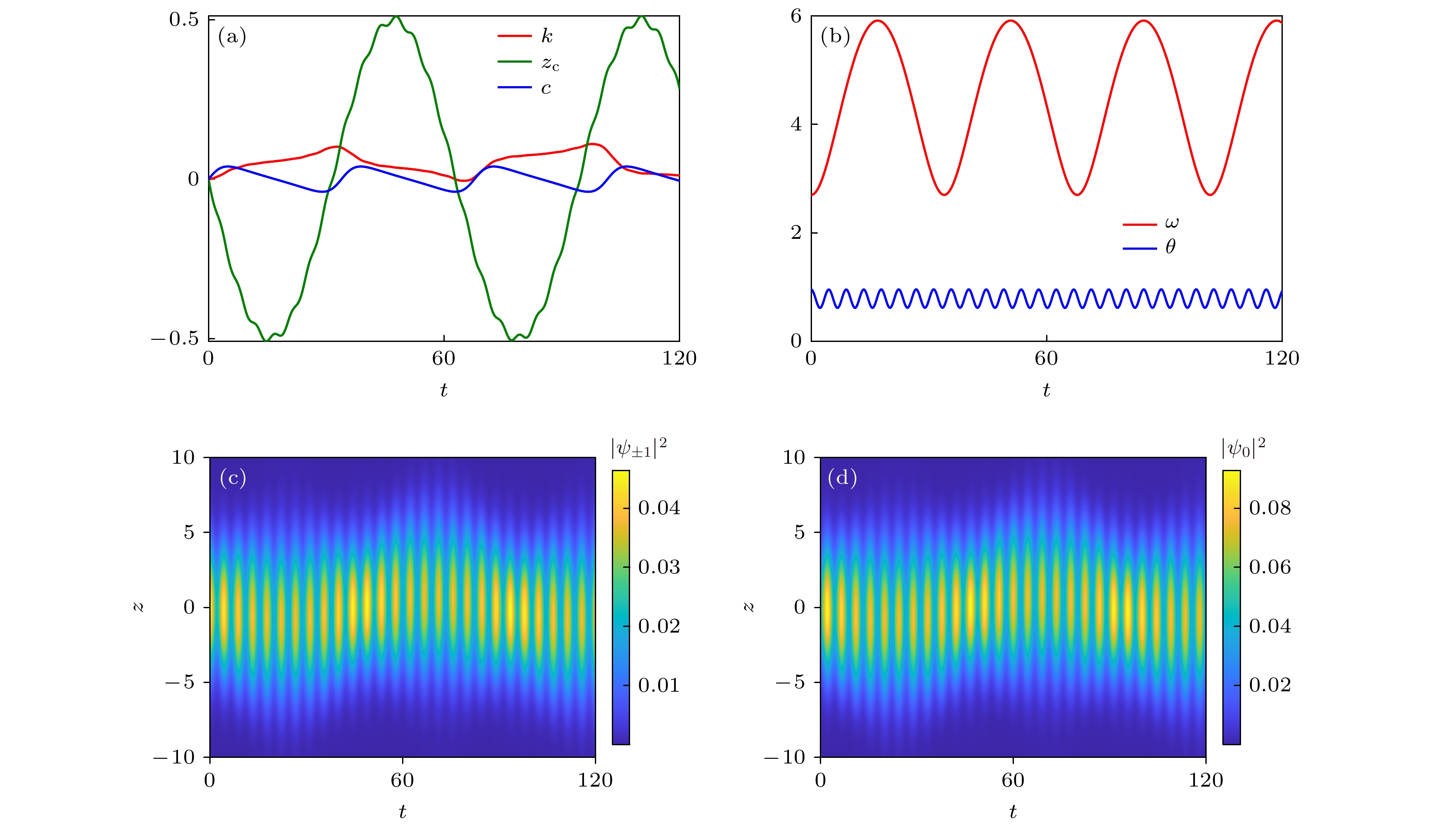
$ \varOmega/k_\text{R}^2 $ , where$ g_\text{n}/k_\text{R} = 1 $ ,$ g_\text{s}/k_\text{R} = 0.1 $ and$ \gamma/k_\text{R}^2 = 0.1 $ 
图 4 (a), (b)变分参数随时间的演化; (c), (d)各分量的密度随时间的演化(GP方程的数值解), 其中系统参数为
$ \varOmega = 1 $ ,$ k_\text{R}=\gamma = 0.1 $ ,$ g_\text{n} = 1 $ 和$ g_\text{s} = 0.1 $ Figure 4. (a), (b) Evolutions of the variational parameters; (c), (d) evolutions of the densities of each components given by the GP simulation, where the parameters are
$ \varOmega = 1 $ ,$ k_\text{R}=\gamma = 0.1 $ ,$ g_\text{n} = 1 $ and$ g_\text{s} = 0.1 $ -
[1] Qi X L, Zhang S C 2010 Phys. Today 63 33
Google Scholar
[2] Lin Y J, Jiménez-GarcÍa K, Spielman I B 2011 Nature 471 83
Google Scholar
[3] Zhang J Y, Ji S C, Chen Z, Zhang L, Du Z D, Yan B, Pan G S, Zhao B, Deng Y J, Zhai H, Chen S, Pan J W 2012 Phys. Rev. Lett. 109 115301
Google Scholar
[4] Wang P, Yu Z Q, Fu Z, Miao J, Huang L, Chai S, Zhai H, Zhang J 2012 Phys. Rev. Lett. 109 095301
Google Scholar
[5] Cheuk L W, Sommer A T, Hadzibabic Z, Yefsah T, Bakr W S, Zwierlein M W 2012 Phys. Rev. Lett. 109 095302
Google Scholar
[6] Chen H R, Lin K Y, Chen P K, Chiu N C, Wang J B, Chen C A, Huang P P, Yip S K, Kawaguchi Y, Lin Y J 2018 Phys. Rev. Lett. 121 113204
Google Scholar
[7] Chen P K, Liu L R, Tsai M J, Chiu N C, Kawaguchi Y, Yip S K, Chang M S, Lin Y J 2018 Phys. Rev. Lett. 121 250401
Google Scholar
[8] Zhang D, Gao T, Zou P, Kong L, Li R, Shen X, Chen X L, Peng S G, Zhan M, Pu H, Jiang K 2019 Phys. Rev. Lett. 122 110402
Google Scholar
[9] Kawaguchi Y, Ueda M 2012 Phys. Rep. 520 253
Google Scholar
[10] Li D, Huang L, Peng P, Bian G, Wang P, Meng Z, Chen L, Zhang J 2020 Phys. Rev. A 102 013309
Google Scholar
[11] Luo X W, Sun K, Zhang C 2017 Phys. Rev. Lett. 119 193001
Google Scholar
[12] Chen L, Zhang Y, Pu H 2020 Phys. Rev. Lett. 125 195303
Google Scholar
[13] Hu H, Hou J, Zhang F, Zhang C 2018 Phys. Rev. Lett. 120 240401
Google Scholar
[14] Lei Z, Deng Y, Lee C 2022 Phys. Rev. Res. 4 033008
Google Scholar
[15] Sun J, Chen Y, Chen X, Zhang Y 2020 Phys. Rev. A 101 053621
Google Scholar
[16] Liu Y, Liu Y K 2021 Mod. Phys. Lett. B 35 2150232
Google Scholar
[17] Campbell D L, Price R M, Putra A, Valdes-Curiel A, Trypogeorgos D, Spielman I B 2016 Nat. Commun. 7 10897
Google Scholar
[18] Xue M, Li X, Ye W, Chen J J, Xu Z F, You L 2022 Phys. Rev. A 106 033708
Google Scholar
[19] Masson S J, Barrett M D, Parkins S 2017 Phys. Rev. Lett. 119 213601
Google Scholar
[20] Davis E J, Bentsen G, Homeier L, Li T, Schleier-Smith M H 2019 Phys. Rev. Lett. 122 010405
Google Scholar
[21] Periwal A, Cooper E S, Kunkel P, Wienand J F, Davis E J, Schleier-Smith M 2021 Nature 600 630
Google Scholar
[22] Diener R B, Ho T L 2006 Phys. Rev. Lett. 96 190405
Google Scholar
[23] Mueller E J 2004 Phys. Rev. A 69 033606
Google Scholar
[24] Natu S S, Li X, Cole W S 2015 Phys. Rev. A 91 023608
Google Scholar
[25] Malomed B A 2006 Soliton Management in Periodic Systems (Vol. 1) (Berlin: Springer) pp27−29
[26] Liu W, Cai Y 2021 SIAM J. Sci. Comput. 43 B219
Google Scholar
[27] Williams J, Walser R, Cooper J, Cornell E, Holland M 2000 Phys. Rev. A 61 033612
Google Scholar
[28] Öhberg P, Stenholm S 1999 Phys. Rev. A 59 3890
Google Scholar
[29] Lee C, Shi L, Gao K 2004 Phys. Rev. A 69 033611
Google Scholar
[30] Bao W, Cai Y 2018 Commun. Comput. Phys. 24 899
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3498
- PDF Downloads: 143
- Cited By: 0
