-
In this work, the conductivity of intrinsic GaSe, S doped 2.5 mass% GaSe (GaSe: S(2.5%)), and S doped 7 mass% GaSe (GaSe: S(7%)) crystals, in a frequency range of 0.3–2.5 THz, is measured by transmission terahertz time-domain spectroscopy, and fitted with Drude-Smith-Lorentz model which is introduced by lattice vibration effect. It is found that the real part of conductivity decreases with the augment of S doping, which is caused by the gradual shift of the Fermi energy level of GaSe crystals to the charge neutrality level due to the generation of substitution impurities and gap impurities by S doping, resulting in the reduction of carrier concentration. The intrinsic GaSe and GaSe: S(2.5%) have a clear lattice vibration peak at about 0.56 THz, while GaSe: S(7%) has no lattice vibration peak near 0.56 THz, which is mainly due to the S doping increasing the structural hardness of the crystal and reducing the interlayer rigidity vibration of the crystal. All three samples have the obvious narrow lattice vibration peaks at about 1.81 THz, and the intensities that first decrease and then increase with the augment of S doping, which is mainly due to the fact that a small amount of S doping can reduce the local structural defects of GaSe and weaken the intensity of the narrow lattice vibration peak, while excessive S doping can generate the β-type GaS crystal, increase the local structural defects of the crystals and the intensity of the narrow lattice vibration peak. With the increase of S doping, the intensity of the broad lattice vibration peak of GaSe crystal weakens or even disappears at about 1.07 THz and 2.28 THz, mainly due to the S doping resulting in the substitution of S for impurities and GaS gap impurities, which reduces the fundamental frequency phonon vibration intensity, thereby weakening the lattice vibration caused by the second-order phonon difference mode of the crystal. The results show that the appropriate concentration of S doping can effectively suppress the lattice vibration of GaSe crystal and reduce the conductivity and power loss in the THz band. This study provides important data support and theoretical basis for the design and fabrication of low loss THz devices.
-
Keywords:
- terahertz time-domain spectroscopy /
- sulfur doped gallium selenide crystal /
- conductivity /
- Drude-Smith-Lorentz model
[1] 杜辉, 陈巧, 刘婷, 贺毅, 金应荣 2022 材料导报 36 24
Du H, Chen Q, Liu T, He Y, Jin Y R 2022 Mater. Rep. 36 24
[2] Liao Y L, Shan Y X, Wu L M, Xiang Y J, Dai XY 2020 Adv. Opt. Mater. 8 1901862
Google Scholar
[3] Sotodeian M, Marandi M 2021 Sol. Energy 221 418
Google Scholar
[4] Kim S J, Kang B J, Puc U, Kim W T, Jazbinsek M, Rotermund F, Kwon O P 2021 Adv. Opt. Mater. 9 2101019
Google Scholar
[5] Niranjan M K 2021 Phys. Rev. B 103 195437
Google Scholar
[6] Guo J, Xie J J, Li D J, Yang G L, Chen F, Wang C R, Zhang L M, Andreev Y M, Kokh K A, Lanskii G V, Svetlichnyi V A 2015 Light-Sci. Appl. 4 e362
Google Scholar
[7] Sheng W, Tang F, Zhang Z L, Chen Y P, Peng X Y, Sheng Z M 2021 Opt. Express 29 8676
Google Scholar
[8] Song Q Y, Yuan X M, Lin Q G, Zhong H Z, Zeng X K, Cai Y, Lu X W, Zheng M J, Cao W H, Xu S X 2021 Opt. Express 29 43379
Google Scholar
[9] Sato Y, Nakajima M, Tang C, Watananbe K, Tanabe T, Oyama Y 2020 Opt. Express 28 20888
Google Scholar
[10] Sorifi S, Moun M, Kaushik S, Singh R 2020 ACS Appl. Electron. Mater. 2 670
Google Scholar
[11] Zhao Y F, Fuh H R, Coileain C O, et al. 2020 Adv. Mater. Technol-US 5 1901085
Google Scholar
[12] Chen J H, He X J, Sa B S, Zhou J, Xu C, Wen C L, Sun Z M 2019 Nanoscale 11 6431
Google Scholar
[13] Liu J, Li J W, Gu L X, Wu H, et al. 2022 Appl. Surf. Sci. 586 152774
Google Scholar
[14] Ku S A, Chu W C, Luo C W, et al. 2012 Opt. Express 20 5029
Google Scholar
[15] Bejani M, Pulci O, Barvestani J, Vala A S, Bechstedt F, Cannuccia E 2019 Phys. Rev. Mater. 3 124003
Google Scholar
[16] Huang C B, Mao M S, Wu H X, Wang Z Y, Ni Y B 2017 J. Cryst. Growth 483 318
Google Scholar
[17] Rak Z, Mahanti S D, Mandal K C, Fernelius N C 2010 Phys. Rev. B 82 155203
Google Scholar
[18] Huang C B, Ni Y B, Wu H X, Wang Z Y, Xiao R C, Qi M 2015 J. Inorg. Mater. 30 887
Google Scholar
[19] Molloy J F, Naftaly M, Andreev Y, Kokh K, Lanskii G, Svetlichnyi V 2014 Opt. Mater. Express 4 2451
Google Scholar
[20] Kokh K A, Molloy J F, Naftaly M, et al. 2015 Mater. Chem. Phys. 154 152
Google Scholar
[21] Huang J G, Huang Z M, Tong J C, Ouyang C, Chu J H, Andreev Y, Kokh K, Lanskii G, Shaiduko A 2013 Appl. Phys. Lett. 103 081104
Google Scholar
[22] Li G F, Huang R J, Huang J G, Zhang W J, Cui H Y, Xia N H, Huang Z M, Chu J H, Ma H Z 2021 Appl. Phys. Express 14 072004
Google Scholar
[23] Molloy J F, Naftaly M, Andreev Y M, Lanskii G V, Lapin I N, Potekaev A I, Kokh K A, Shabalina A V, Shaiduko A V, Svetlichnyi V A 2014 Crystengcomm 16 1995
Google Scholar
[24] 刘泉澄, 张祺, 李桂琳, 何向阳, 邓琥, 尚丽平 2021 光学学报 41 238
Liu Q C, Zhang Q, Li G L, He X Y, Deng H, Shang L P 2021 Acta Opt. Sin. 41 238
[25] Yu B L, Zeng F, Kartazayev V, Alfano R R 2005 Appl. Phys. Lett. 87 182104
Google Scholar
[26] Palik E D 1998 Handbook of Optical Constants of Solids (Vol. 3) (San Dicgo: Academic Press) pp473–477
[27] 黄昆, 韩汝琦 1988 固体物理学 (北京: 高等教育出版社) 第440页
Huang K, Han R Q 1988 The Physics of Solids (Beijing: Higher Education Press) p440 (in Chinese)
[28] Naftaly M, Molloy J F, Andreev Y M, Kokh K A, Lanskii G V, Svetlichnyi V A 2015 Opt. Express 23 32820
Google Scholar
[29] Manfredotti C, Mancini A M, Rizzo A, Murri R, Vasanelli L 1978 Phys. Status Solidi A 48 293
[30] Ma T H, Li Z Q, Zhang H C, Zhu C Q, Lei Z T, Yang C H 2021 Mater. Today Commu. 27 102212
Google Scholar
[31] Yoshida J, Nakashima S, Mitsuishi A 1973 Phys. Stat. Sol. 59 655
Google Scholar
[32] Kuroda N, Ueno O, Nishina Y 1987 Phys. Rev. B Condens. Matter. 35 3860
Google Scholar
[33] Zhang D W, Lv Z H, Sun L, Shao Z Z, Yuan J M 2008 33rd International Conference on Infrared, Millimeter and Terahertz Waves Pasadena, CA September 15–19, 2008 p267
[34] Molas M R, Tyurnina A V, Zolyomi V, Ott A K, Terry D J, Hamer M J, Yelgel C, Babinski A, Nasibulin A G, Ferrari A C, Falko V I, Gorbachev R 2021 Faraday Discuss. 227 163
Google Scholar
[35] Niranjan M K 2021 Physical Review B 103 195437
[36] Willis K J, Hagness S C, Knezevic I 2013 Appl. Phys. Lett. 102 122113
Google Scholar
[37] Jensen S A 2014 Ph. D. Dissertation (Van der Waals-Zeeman Institute) pp32–37
[38] Das A C, Bhattacharya S, Jewariya M, Prabhu S S, Mandal K C, Ozaki T, Datta P K 2017 IEEE J. Sel. Top. Quant. 23 8400707
Google Scholar
[39] Jin Z M, Peng Y, Fang Y Q, et al. 2022 Light-SCI Appl. 11 209
Google Scholar
[40] Brudnyi V N, Kosobutsky A V, Sarkisov S Y 2010 Semiconductors 44 1158
Google Scholar
[41] Atuchin V V, Bereznaya S A, Beisel N F, et al. 2014 Mater. Chem. Phys. 146 12
Google Scholar
[42] Stefancu A, Lee S, Zhu L, Liu M, Lucacel R C, Cortes E, Leopold N 2021 Nano Lett. 21 6592
Google Scholar
[43] 刘恩科, 朱秉升, 罗晋生 2017 半导体物理学 (北京: 电子工业出版社) 第93页
Liu E K, Zhu B S, Luo J S 2017 The Physics of Semiconductors (Beijing: Publishing House of Electronics Industy) p93 (in Chinese)
-
图 1 透射式THz-TDS系统实验装置示意图
Figure 1. Schematic diagram of experimental setup of transmission THz-TDS system.
图 2 (a)参考信号、GaSe、GaSe: S(2.5%) 和GaSe: S(7%) 的THz时域光谱图, 插图是3个样品THz时域光谱主峰的放大图; (b) 参考信号、GaSe、GaSe: S(2.5%) 和GaSe: S(7%) 的THz频谱图; (c) GaSe、GaSe: S(2.5%) 和GaSe: S(7%) 在THz波段的透射率
Figure 2. (a) THz time-domain spectra of the reference signal GaSe, GaSe: S(2.5%), and GaSe: S (7%), the illustration is a magnified view of the main peak of THz time-domain spectrum of three samples; (b) THz spectra of the reference signal GaSe, GaSe: S(2.5%), and GaSe: S(7%); (c) transmissivity of GaSe, GaSe: S(2.5%), and GaSe: S(7%) in THz band.
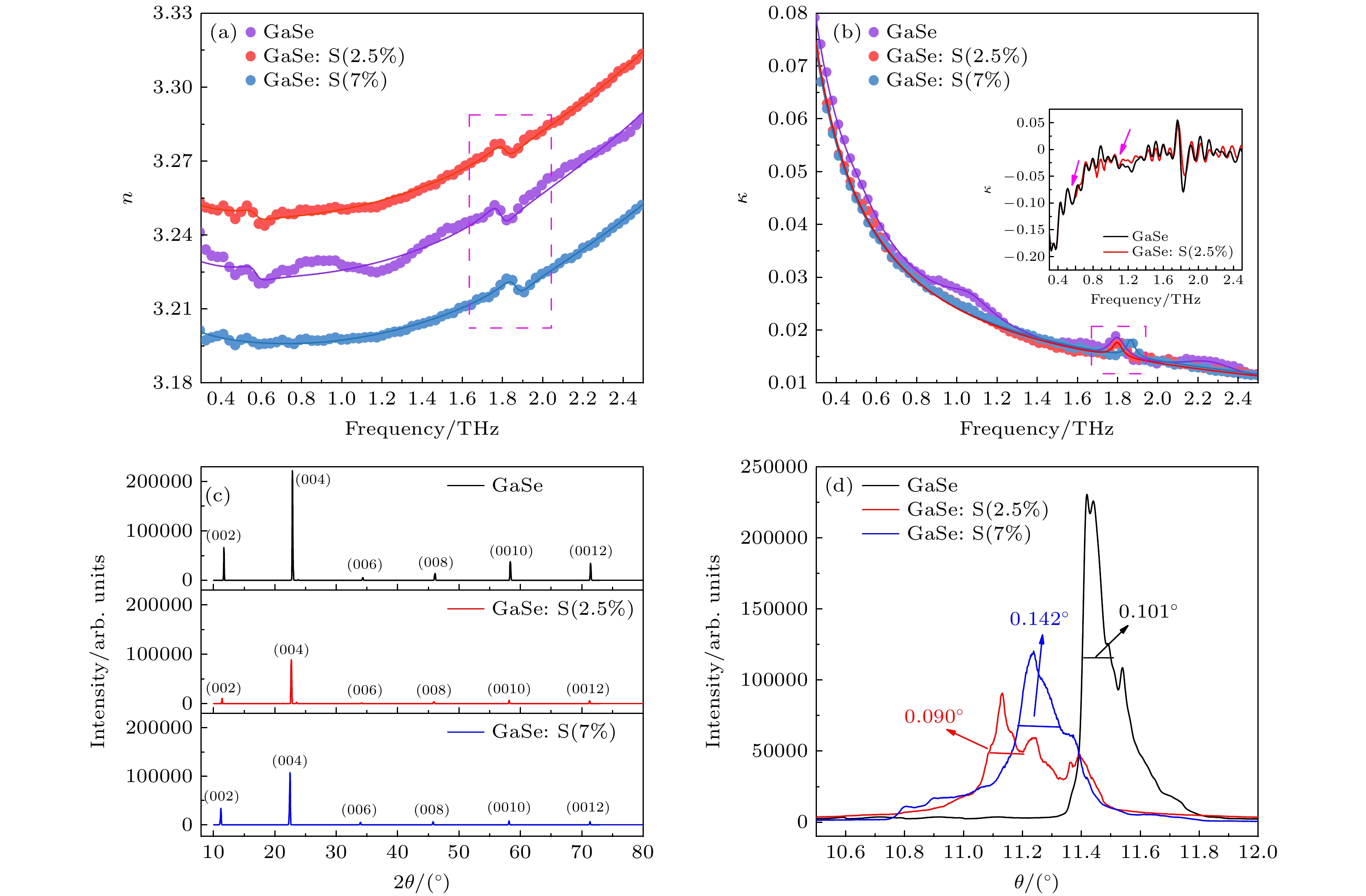
图 3 (a) GaSe、GaSe: S(2.5%) 和GaSe: S(7%) 在THz波段的折射率; (b) GaSe、GaSe: S(2.5%) 和GaSe: S(7%) 在THz波段的消光系数(实线是折射率和消光系数的拟合结果), 插图是GaSe和GaSe: S(2.5%) 消光系数的一阶导数; (c) GaSe、GaSe: S(2.5%) 和GaSe: S(7%) 的XRD图; (d) GaSe、GaSe: S(2.5%) 和GaSe: S(7%) (004)晶面的摇摆曲线图
Figure 3. (a) Refractive indexes of GaSe, GaSe: S(2.5%), and GaSe: S(7%) in THz band; (b) extinction coefficients of GaSe, GaSe: S(2.5%), and GaSe: S(7%) in THz band (the solid lines are the results of refractive index and extinction coefficient fittings), the illustration is a first-order derivative of GaSe and GaSe: S(2.5%) extinction coefficients; (c) the X-ray diffraction pattern of GaSe, GaSe: S(2.5%), and GaSe: S(7%); (d) the rocking curve of the (004) face of GaSe, GaSe: S(2.5%), and GaSe: S(7%).
图 4 GaSe, GaSe: S(2.5%) 和GaSe: S(7%) 在THz波段的吸收系数(实线是吸收系数的拟合结果)
Figure 4. Absorption coefficients of GaSe, GaSe: S(2.5%), and GaSe: S(7%) in THz band (the solid lines are the results of absorption coefficients fittings).
图 5 (a) GaSe、GaSe: S(2.5%)和GaSe: S(7%)在THz波段的电导率实部; (b) GaSe, GaSe: S(2.5%)和GaSe: S(7%)在THz波段的电导率虚部(实线是Drude-Smith-Lorentz模型拟合结果)
Figure 5. (a) The real part of conductivity of GaSe, GaSe: S(2.5%), and GaSe: S(7%) in THz band; (b) the imaginary part of conductivity of GaSe, GaSe: S(2.5%), and GaSe: S(7%) in THz band (the solid lines are the results of an improved Drude-Smith-Lorentz model fitting).
图 6 (a) GaSe, GaSe: S(2.5%)和GaSe: S(7%)的复折射率、吸收系数和复电导率在Drude-Smith-Lorentz模型下的等离子体频率和载流子恢复过程的复合时间及其平均值; (b) GaSe, GaSe: S(2.5%)和GaSe: S(7%)分别的复折射率、吸收系数和复折射率在Drude-Smith-Lorentz模型下的系统的恢复力或反向散射度c1及其平均值
Figure 6. (a) The values of the plasma frequency, the complex time of the carrier recovery process and their average for GaSe, GaSe: S(2.5%), and GaSe: S(7%) under the Drude-Smith-Lorentz model of complex conductivity, complex refractivity and absorption coefficient; (b) the values of the recovery force or backscattering degree of the system and the average for GaSe, GaSe: S (2.5%), and GaSe: S(7%) under the Drude-Smith-Lorentz model of complex conductivity, complex refractivity and absorption coefficient
表 1 复折射率的晶格振动强度和声子驰豫速率的拟合结果
Table 1. The fitting results of lattice vibration intensity and phonon relaxation rate of the complex refractivity.
物理参数 GaSe GaSe: S(2.5%) GaSe: S(7%) $ {\omega _{o1}} $/THz 0.56 0.56 $ {S_1} $/(arb.units) 0.0016 0.0015 $ {\varGamma _1} $/THz 0.0411 0.0413 $ {\omega _{o2}} $/THz 1.07 1.07 $ {S_2} $/(arb.units) 0.0112 0.0011 $ {\varGamma _2} $/THz 0.2882 0.6270 $ {\omega _{o3}} $/THz 1.81 1.81 1.81 $ {S_3} $/(arb.units) 0.0010 0.0008 0.0009 $ {\varGamma _3} $/THz 0.0412 0.0647 0.0573 $ {\omega _{o4}} $/THz 2.28 $ {S_4} $/(arb.units) 0.0042 $ {\varGamma _4} $/THz 0.3631 
DownLoad: CSV
表 2 吸收系数的晶格振动强度和声子驰豫速率的拟合结果
Table 2. The fitting results of lattice vibration intensity and phonon relaxation rate of the absorption coefficient.
物理参数 GaSe GaSe: S(2.5%) GaSe: S(7%) $ {\omega _{o1}} $/THz 0.56 0.56 $ {S_1} $/(arb.units) 0.0039 0.0021 $ {\varGamma _1} $/THz 0.4112 0.4513 $ {\omega _{o2}} $/THz 1.07 1.07 $ {S_2} $/(arb.units) 0.0081 0.0039 $ {\varGamma _2} $/THz 0.2229 0.2213 $ {\omega _{o3}} $/THz 1.81 1.81 1.81 $ {S_3} $/(arb.units) 0.0003 0.0001 0.0002 $ {\varGamma _3} $/THz 0.0766 0.0787 0.0777 $ {\omega _{o4}} $/THz 2.28 $ {S_4} $/(arb.units) 0.0048 $ {\varGamma _4} $/THz 0.4012
DownLoad: CSV
表 3 复电导率的晶格振动强度和声子驰豫速率的拟合结果
Table 3. The fitting results of lattice vibration intensity and phonon relaxation rate of the complex conductivity.
物理参数 GaSe GaSe: S(2.5%) GaSe: S(7%) $ {\omega _{o1}} $/THz 0.56 0.56 $ {S_1} $/(arb.units) 0.0055 0.0052 $ {\varGamma _1} $/THz 1.1491 1.1495 $ {\omega _{o2}} $/THz 1.07 1.07 $ {S_2} $/(arb.units) 0.0044 0.0020 $ {\varGamma _2} $/THz 1.3296 1.3936 $ {\omega _{o3}} $/THz 1.81 1.81 1.81 $ {S_3} $/(arb.units) 0.0009 0.0007 0.0008 $ {\varGamma _3} $/THz 0.4122 0.4385 0.4245 $ {\omega _{o4}} $/THz 2.28 $ {S_4} $/(arb.units) 0.0018 $ {\varGamma _4} $/THz 1.9465
DownLoad: CSV
表 4 晶格振动强度和声子驰豫速率多次拟合结果各自的平均值
Table 4. The averages value of lattice vibration intensity and phonon relaxation rate from multiple fitting results.
物理参数 GaSe GaSe: S(2.5%) GaSe: S(7%) $ {\omega _{o1}} $/THz 0.56 0.56 $ {S_1} $/(arb.units) 0.0037 0.0029 $ {\varGamma _1} $/THz 0.5338 0.5474 $ {\omega _{o2}} $/THz 1.07 1.07 $ {S_2} $/(arb.units) 0.0079 0.0023 $ {\varGamma _2} $/THz 0.6136 0.7473 $ {\omega _{o3}} $/THz 1.81 1.81 1.81 $ {S_3} $/(arb.units) 0.0007 0.0005 0.0006 $ {\varGamma _3} $/THz 0.1767 0.1940 0.1865 $ {\omega _{o4}} $/THz 2.28 $ {S_4} $/(arb.units) 0.0036 $ {\varGamma _4} $/THz 0.9036
DownLoad: CSV
-
[1] 杜辉, 陈巧, 刘婷, 贺毅, 金应荣 2022 材料导报 36 24
Du H, Chen Q, Liu T, He Y, Jin Y R 2022 Mater. Rep. 36 24
[2] Liao Y L, Shan Y X, Wu L M, Xiang Y J, Dai XY 2020 Adv. Opt. Mater. 8 1901862
Google Scholar
[3] Sotodeian M, Marandi M 2021 Sol. Energy 221 418
Google Scholar
[4] Kim S J, Kang B J, Puc U, Kim W T, Jazbinsek M, Rotermund F, Kwon O P 2021 Adv. Opt. Mater. 9 2101019
Google Scholar
[5] Niranjan M K 2021 Phys. Rev. B 103 195437
Google Scholar
[6] Guo J, Xie J J, Li D J, Yang G L, Chen F, Wang C R, Zhang L M, Andreev Y M, Kokh K A, Lanskii G V, Svetlichnyi V A 2015 Light-Sci. Appl. 4 e362
Google Scholar
[7] Sheng W, Tang F, Zhang Z L, Chen Y P, Peng X Y, Sheng Z M 2021 Opt. Express 29 8676
Google Scholar
[8] Song Q Y, Yuan X M, Lin Q G, Zhong H Z, Zeng X K, Cai Y, Lu X W, Zheng M J, Cao W H, Xu S X 2021 Opt. Express 29 43379
Google Scholar
[9] Sato Y, Nakajima M, Tang C, Watananbe K, Tanabe T, Oyama Y 2020 Opt. Express 28 20888
Google Scholar
[10] Sorifi S, Moun M, Kaushik S, Singh R 2020 ACS Appl. Electron. Mater. 2 670
Google Scholar
[11] Zhao Y F, Fuh H R, Coileain C O, et al. 2020 Adv. Mater. Technol-US 5 1901085
Google Scholar
[12] Chen J H, He X J, Sa B S, Zhou J, Xu C, Wen C L, Sun Z M 2019 Nanoscale 11 6431
Google Scholar
[13] Liu J, Li J W, Gu L X, Wu H, et al. 2022 Appl. Surf. Sci. 586 152774
Google Scholar
[14] Ku S A, Chu W C, Luo C W, et al. 2012 Opt. Express 20 5029
Google Scholar
[15] Bejani M, Pulci O, Barvestani J, Vala A S, Bechstedt F, Cannuccia E 2019 Phys. Rev. Mater. 3 124003
Google Scholar
[16] Huang C B, Mao M S, Wu H X, Wang Z Y, Ni Y B 2017 J. Cryst. Growth 483 318
Google Scholar
[17] Rak Z, Mahanti S D, Mandal K C, Fernelius N C 2010 Phys. Rev. B 82 155203
Google Scholar
[18] Huang C B, Ni Y B, Wu H X, Wang Z Y, Xiao R C, Qi M 2015 J. Inorg. Mater. 30 887
Google Scholar
[19] Molloy J F, Naftaly M, Andreev Y, Kokh K, Lanskii G, Svetlichnyi V 2014 Opt. Mater. Express 4 2451
Google Scholar
[20] Kokh K A, Molloy J F, Naftaly M, et al. 2015 Mater. Chem. Phys. 154 152
Google Scholar
[21] Huang J G, Huang Z M, Tong J C, Ouyang C, Chu J H, Andreev Y, Kokh K, Lanskii G, Shaiduko A 2013 Appl. Phys. Lett. 103 081104
Google Scholar
[22] Li G F, Huang R J, Huang J G, Zhang W J, Cui H Y, Xia N H, Huang Z M, Chu J H, Ma H Z 2021 Appl. Phys. Express 14 072004
Google Scholar
[23] Molloy J F, Naftaly M, Andreev Y M, Lanskii G V, Lapin I N, Potekaev A I, Kokh K A, Shabalina A V, Shaiduko A V, Svetlichnyi V A 2014 Crystengcomm 16 1995
Google Scholar
[24] 刘泉澄, 张祺, 李桂琳, 何向阳, 邓琥, 尚丽平 2021 光学学报 41 238
Liu Q C, Zhang Q, Li G L, He X Y, Deng H, Shang L P 2021 Acta Opt. Sin. 41 238
[25] Yu B L, Zeng F, Kartazayev V, Alfano R R 2005 Appl. Phys. Lett. 87 182104
Google Scholar
[26] Palik E D 1998 Handbook of Optical Constants of Solids (Vol. 3) (San Dicgo: Academic Press) pp473–477
[27] 黄昆, 韩汝琦 1988 固体物理学 (北京: 高等教育出版社) 第440页
Huang K, Han R Q 1988 The Physics of Solids (Beijing: Higher Education Press) p440 (in Chinese)
[28] Naftaly M, Molloy J F, Andreev Y M, Kokh K A, Lanskii G V, Svetlichnyi V A 2015 Opt. Express 23 32820
Google Scholar
[29] Manfredotti C, Mancini A M, Rizzo A, Murri R, Vasanelli L 1978 Phys. Status Solidi A 48 293
[30] Ma T H, Li Z Q, Zhang H C, Zhu C Q, Lei Z T, Yang C H 2021 Mater. Today Commu. 27 102212
Google Scholar
[31] Yoshida J, Nakashima S, Mitsuishi A 1973 Phys. Stat. Sol. 59 655
Google Scholar
[32] Kuroda N, Ueno O, Nishina Y 1987 Phys. Rev. B Condens. Matter. 35 3860
Google Scholar
[33] Zhang D W, Lv Z H, Sun L, Shao Z Z, Yuan J M 2008 33rd International Conference on Infrared, Millimeter and Terahertz Waves Pasadena, CA September 15–19, 2008 p267
[34] Molas M R, Tyurnina A V, Zolyomi V, Ott A K, Terry D J, Hamer M J, Yelgel C, Babinski A, Nasibulin A G, Ferrari A C, Falko V I, Gorbachev R 2021 Faraday Discuss. 227 163
Google Scholar
[35] Niranjan M K 2021 Physical Review B 103 195437
[36] Willis K J, Hagness S C, Knezevic I 2013 Appl. Phys. Lett. 102 122113
Google Scholar
[37] Jensen S A 2014 Ph. D. Dissertation (Van der Waals-Zeeman Institute) pp32–37
[38] Das A C, Bhattacharya S, Jewariya M, Prabhu S S, Mandal K C, Ozaki T, Datta P K 2017 IEEE J. Sel. Top. Quant. 23 8400707
Google Scholar
[39] Jin Z M, Peng Y, Fang Y Q, et al. 2022 Light-SCI Appl. 11 209
Google Scholar
[40] Brudnyi V N, Kosobutsky A V, Sarkisov S Y 2010 Semiconductors 44 1158
Google Scholar
[41] Atuchin V V, Bereznaya S A, Beisel N F, et al. 2014 Mater. Chem. Phys. 146 12
Google Scholar
[42] Stefancu A, Lee S, Zhu L, Liu M, Lucacel R C, Cortes E, Leopold N 2021 Nano Lett. 21 6592
Google Scholar
[43] 刘恩科, 朱秉升, 罗晋生 2017 半导体物理学 (北京: 电子工业出版社) 第93页
Liu E K, Zhu B S, Luo J S 2017 The Physics of Semiconductors (Beijing: Publishing House of Electronics Industy) p93 (in Chinese)
-
[1] Zheng Jian-Jun, Zhang Li-Ping. Monolayer Cu2X (X=S, Se): excellent thermoelectric material with low lattice thermal conductivity. Acta Physica Sinica, 2023, 0(0): 0-0. doi: 10.7498/aps.72.20220015 [2] Fang Yu-Qing, Jin Zuan-Ming, Chen Hai-Yang, Ruan Shun-Yi, Li Ju-Geng, Cao Shi-Xun, Peng Yan, Ma Guo-Hong, Zhu Yi-Ming. Terahertz spectroscopic characterization of spin mode and crystal-field transition in high-throughput grown $ {\bf Sm}_{ x}{\bf Pr}_{ 1– x}{\bf FeO_3} $ crystals. Acta Physica Sinica, 2020, 69(20): 209501. doi: 10.7498/aps.69.20200732[3] Ren Zhuang, Cheng Long, Sergei Guretskii, Nadzeya Liubochko, Li Jiang-Tao, Shang Jia-Min, Sergei Barilo, Wu An-Hua, Alexandra Kalashnikova, Ma Zong-Wei, Zhou Chun, Sheng Zhi-Gao. Terahertz spectroscopy study of doping and magnetic field induced effects on spin reorientation in Ho1–xYxFeO3 single crystals. Acta Physica Sinica, 2020, 69(20): 207802. doi: 10.7498/aps.69.20201518 [4] Du Yi-Shuai, Kang Wei, Zheng Rui-Lun. Variations of the electrical conductivity and the Fermi velocity of epitaxial graphene with temperature. Acta Physica Sinica, 2017, 66(1): 014701. doi: 10.7498/aps.66.014701 [5] Fu Zhi-Jian, Jia Li-Jun, Xia Ji-Hong, Tang Ke, Li Zhao-Hong, Quan Wei-Long, Chen Qi-Feng. A simple and effective simulation for electrical conductivity of warm dense titanium. Acta Physica Sinica, 2016, 65(6): 065201. doi: 10.7498/aps.65.065201 [6] Meng Zeng-Rui, Zhang Wei-Bin, Du Yu, Shang Li-Ping, Deng Hu. Terahertz spectrum and simulation of the phase transformation of FOX-7. Acta Physica Sinica, 2015, 64(7): 073302. doi: 10.7498/aps.64.073302 [7] Zheng Shu-Wen, Fan Guang-Han, He Miao, Zhao Ling-Zhi. Theoretical study of the effect of W-doping on the conductivity of β-Ga2O3. Acta Physica Sinica, 2014, 63(5): 057102. doi: 10.7498/aps.63.057102 [8] Yang Jing-Qi, Li Shao-Xian, Zhao Hong-Wei, Zhang Jian-Bing, Yang Na, Jing Dan-Dan, Wang Chen-Yang, Han Jia-Guang. Terahertz study of L-asparagine and its monohydrate. Acta Physica Sinica, 2014, 63(13): 133203. doi: 10.7498/aps.63.133203 [9] Hou Qing-Yu, Lü Zhi-Yuan, Zhao Chun-Wang. Effects of V-heavy-doped ZnO on electric conductivity performance and absorption spectrum. Acta Physica Sinica, 2014, 63(19): 197102. doi: 10.7498/aps.63.197102 [10] Chen Yun-Yun, Zheng Gai-Ge, Gu Fang, Li Zhen-Hua. Effect of dust particle potential on plasma conductivity. Acta Physica Sinica, 2012, 61(15): 154202. doi: 10.7498/aps.61.154202 [11] Hou Qing-Yu, Zao Chun-Wang, Li Ji-Jun, Wang Gang. Frist principles study of effect of high Al doping concentrationof p-type ZnO on electric conductivity performance. Acta Physica Sinica, 2011, 60(4): 047104. doi: 10.7498/aps.60.047104 [12] Hao Zhi-Hong, Hu Zi-Yang, Zhang Jian-Jun, Hao Qiu-Yan, Zhao Ying. Influence of doped PEDOT ∶PSS on performance of polymer solar cells. Acta Physica Sinica, 2011, 60(11): 117106. doi: 10.7498/aps.60.117106 [13] Liu Jian-Jun. First-principles calculation of electronic structure of (Zn,Al)O and analysis of its conductivity. Acta Physica Sinica, 2011, 60(3): 037102. doi: 10.7498/aps.60.037102 [14] Yang Feng-Xia, Zhang Duan-Ming, Deng Zong-Wei, Jiang Sheng-Lin, Xu Jie, Li Shu-Dan. The influence of the matrix electrical conductivity on the dc poling behaviors and the loss of 0-3 ferroelectric composites. Acta Physica Sinica, 2008, 57(6): 3840-3845. doi: 10.7498/aps.57.3840 [15] Jiang Ji-Hao, Wang Gui-Ji, Yang Yu. A new method to measure the electrical conductivity of metals in electric exploding. Acta Physica Sinica, 2008, 57(2): 1123-1127. doi: 10.7498/aps.57.1123 [16] Ma Xiao-Jing, Zhao Hong-Wei, Dai Bin, Liu Gui-Feng. THz spectra of hypoxanthine and inosine. Acta Physica Sinica, 2008, 57(6): 3429-3434. doi: 10.7498/aps.57.3429 [17] Tan Man-Lin, Zhu Jia-Qi, Zhang Hua-Yu, Zhu Zhen-Ye, Han Jie-Cai. Effect of boron doping on the electrical conduction of tetrahedral amorphous carbon films. Acta Physica Sinica, 2008, 57(10): 6551-6556. doi: 10.7498/aps.57.6551 [18] Quan Rong-Hui, Han Jian-Wei, Huang Jian-Guo, Zhang Zhen-Long. Modeling analysis of radiation induced conductivity in electrical insulator. Acta Physica Sinica, 2007, 56(11): 6642-6647. doi: 10.7498/aps.56.6642 [19] Xu Ren-Xin, Chen Wen, Zhou Jing. Effect of polymer conductance on polarization properties of 0-3 piezoelectric composite. Acta Physica Sinica, 2006, 55(8): 4292-4297. doi: 10.7498/aps.55.4292 [20] Shi Yan-Xiang, Ge De-Biao, Wu Jian. Influence of charge and discharge processes of dust particles on the dust plasma conductivity. Acta Physica Sinica, 2006, 55(10): 5318-5324. doi: 10.7498/aps.55.5318
DownLoad:
Catalog
Metrics
- Abstract views: 4250
- PDF Downloads: 93
- Cited By: 0
