-
Surface plasma wave (SPW) will significantly affect the subsequent mutual coupling between laser and plasma, so there are many important applications such as particle acceleration driven by laser pulses and transmission enhancement. In this work, the properties of the SPW produced by an ultra-short and ultra-intensity laser pulse incident on a double-layer plasma target are studied by using the all-electromagnetic large-scale two-dimensional particle in cell (PIC) simulations. It is shown that the high-intensity laser incident with a large angle, θ =75°, can drive the electrons of the low-density layer to form a transportable periodic structure with the propagation speed close to light speed, and excite electrostatic wave whose wavelength is similar to that of the incident laser and is numerically close to the theoretical result according to previous theory. In order to excite the SPW, the laser intensity needs to reach a certain threshold. Besides, the ratio of the surface wave intensity to the incident laser intensity in the double-layer target case obviously deviates from the theoretical result of the single-layer target case, showing a nonlinear relationship. In the second part of the simulation, it is found that the SPW can significantly enhance the transmission of subsequent laser pulse, allowing the subsequent laser to break through the "black barrier" due to the dense plasma. A pre-laser irradiates the double-layer plasma target at θ = 75°, and then the subsequent laser is normally incident after a delay of Δt = 23T. As a result, an obvious electromagnetic wave with the same direction as the sub-laser can be observed behind the target, which indicates that the sub-laser absolutely transmits the dense plasma. In comparison, when a single laser is normally incident on the target without pre-laser while other conditions keep unchanged, no obvious wave can be distinguished behind the target, that is, the field is nearly zero. Another simulation where a single-layer target is injected by pre-laser and sub-laser in order but the wave behind the target is also unobservable, proves that it is SPW that plays the main role in transmission enhancement instead of accelerated hot electrons on the target which can also transport the laser energy.
-
Keywords:
- laser-plasma interaction /
- surface plasma wave /
- transmission enhancement /
- numerical simulation
[1] Otto A 1968 Z. Physik 216 398
Google Scholar
[2] Raether H 1988 Surface Plasmons on Smooth and Rough Surfaces and on Gratings (Springer
Google Scholar
[3] Ebbesen T W, Lezec H J, Ghaemi H F, Thio T, Wolff P A 1998 Nature 391 667
Google Scholar
[4] Liu H T, Lalanne P 2008 Nature 452 0672
Google Scholar
[5] Garcia-Vidal F J, Martin-Moreno L, Ebbesen T W 2010 Rev. Mod. Phys. 82 729
Google Scholar
[6] Florian C, Kirner S V, Kruger J, Bonse J 2020 J. Laser Appl. 32 022063
Google Scholar
[7] Ceccotti T, Floquet V, Sgattoni A, et al. 2013 Phys. Rev. Lett. 111 185001
Google Scholar
[8] Clark E L, Krushelnick K, Davies J R, et al. 2006 Phys. Plasma 96 670
Google Scholar
[9] Wilks S C, Langdon A B, Cowan T E, et al. 2001 Phys. Plasmas 8 542
Google Scholar
[10] Xu H, Yu W, Lu P X, Senecha V K, He F, Shen B F, Qian L J, Li R X, Xu Z Z 2005 Phys. Plasmas 12 013105
Google Scholar
[11] Chen L M, Kando M, Xu M H, et al. 2008 Phys. Rev. Lett. 100 045004
Google Scholar
[12] Dobosz S, Doumy G, Stabile H, D’Oliveira P, Monot P, Réau F, Hüller S, Martin Ph 2005 Phys. Rev. Lett. 95 025001
Google Scholar
[13] Zhu X M, Prasad1 R, Swantusch1 M, Aurand B, Andreev A A, Willi1 O, Cerchez M 2020 High Power Laser Sci. Eng. 8 e15
Google Scholar
[14] Marini S, Kleij P S, Amiranoff F, Grech M, Raynaud M 2021 Phys. Plasmas 28 073104
Google Scholar
[15] 胡希伟 2003 等离子体理论基础 (第二版) (北京: 北京大学出版社) 第270页
Hu X W 2003 Theoretical foundation of plasma (Vol. 2) (Beijing: Peking University Press) p270 (in Chinese)
[16] Rulliere C 2007 Femtosecond Laser Pulse Principles and Experiments (2nd Ed.) (Beijing: Science Press)
[17] Liu C S, Tripath V K, Shao X, Liu T C 2015 Phys. Plasma 22 412
Google Scholar
[18] Haider M M, Sheng Z M 2021 AIP Adv. 11 035221
Google Scholar
[19] Dawson J M 1962 Phys. Fluids 5 445
Google Scholar
[20] 张智猛 2011 博士学位论文 (杭州: 浙江大学)
Zhang Z M 2011 Ph. D. Dissertation (Hangzhou: Zhejiang University) (in Chinese)
[21] Zhang Z M, He X T, Sheng Z M, Yu M Y 2010 Phys. Plasma 17 043110
Google Scholar
[22] Zhang Z M, He X T, Sheng Z M, Yu M Y 2011 Phys. Plasma 18 023110
Google Scholar
[23] Sheng Z M, Zhu L W, Yu M Y, Zhang Z M 2010 New J. Phys. 12 013001
Google Scholar
[24] Birdsall C K, Fuss D 1969 Comput. Phys. 3 494
Google Scholar
[25] Yee K S 1966 IEEE Trans. Antennas Propag. 14 302
Google Scholar
[26] Fan G X, Liu Q H 1998 Wiley Subscription Services, Inc. A Wiley Company 19 258
Google Scholar
-
图 1 模拟设置示意图 (长度单位: μm, 密度n1
$\ll $ n2)Figure 1. Schematic diagram of simulation settings (Length unit: μm, Density: n1
$\ll $ n2 ).
图 2 强激光斜入射双层等离子体靶后的电子密度分布, 密度单位: nc, 入射角θ = 75°, 入射光强aL = 2, 入射中心在x = 15μm处, 低密度层厚度为0.5 μm
Figure 2. Electron density distribution after intense laser pulse oblique incidence on double-layer plasma target, the unit of density: nc, incident angle θ = 75°, laser intensity aL = 2, incident center is at x = 15μm, thickness of low-density layer is 0.5 μm.
图 3 (a) 强激光斜入射双层等离子体靶t = 30T时Ex (归一化) 的分布; (b) y = 39.6 μm的直线上的Ex经傅里叶变换后幅度-波数域的结果, k0是入射光在x方向上的波数, 峰值在k/k0 = 1.005处, 表面波强度as = 0.22
Figure 3. (a) The distribution of Ex (normalized) when the intense laser pulse oblique incident on the double-layer plasma target at t = 30T; (b) the result of Fourier transformation of Ex on the line y = 39.6 μm to the amplitude-wavenumber domain, k0 is the incident laser wavenumber in the x direction. The peak value is at k/k0 = 1.005. The amplitude of SPW as = 0.22.
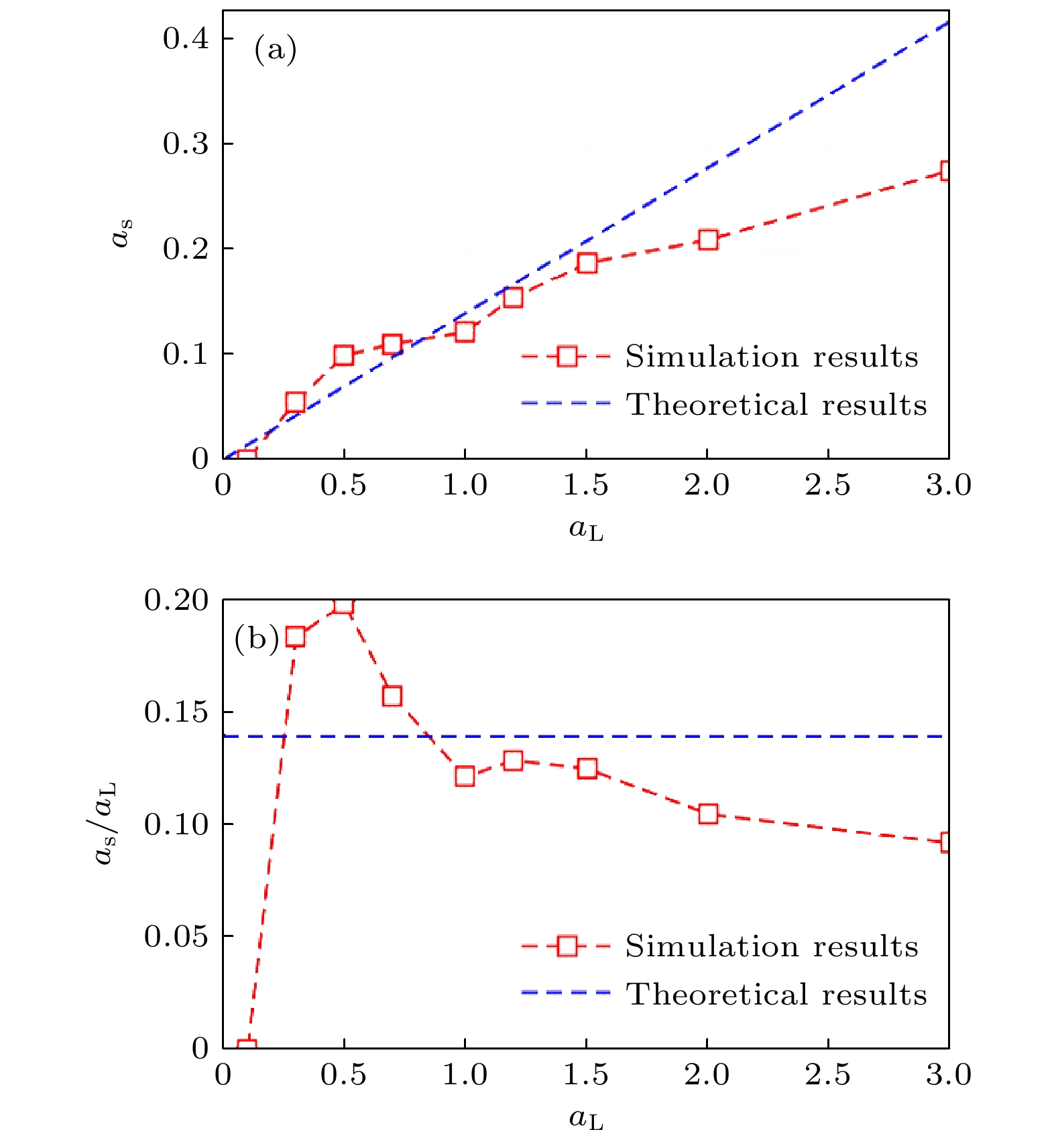
图 4 表面波强度随入射光强的变化曲线, aL ≤ 0.1时无法激发周期性的电子振荡. 红线是入射角θ = 75°入射双层靶的模拟结果, 蓝线是在相同激光强度及等离子体密度的条件下使用有周期性表面结构的单层靶时的理论结果, 斜率as
/aL = 0.139 (a) as-aL曲线; (b) as /aL-aL曲线 Figure 4. The curve of the amplitude of SPW with incident laser intensity. When aL ≤ 0.1, periodic electron oscillation cannot be excited. The red line is the simulation result of double-layer target with incident angle θ = 75°, and the blue line is the theoretical result when using single-layer target with ripped surface under the same laser intensity and plasma density, the slope as/aL = 0.139: (a) The curve of as-aL; (b) the curve of as/aL-aL.
图 5 入射角θ = 85°时表面电子密度分布 (a) t = 25 T; (b) t = 30T, 密度单位: nc
Figure 5. The distribution of surface electron density when incidence angle θ = 85°: (a) t = 25T; (b) t = 30T, the unit of density: nc.
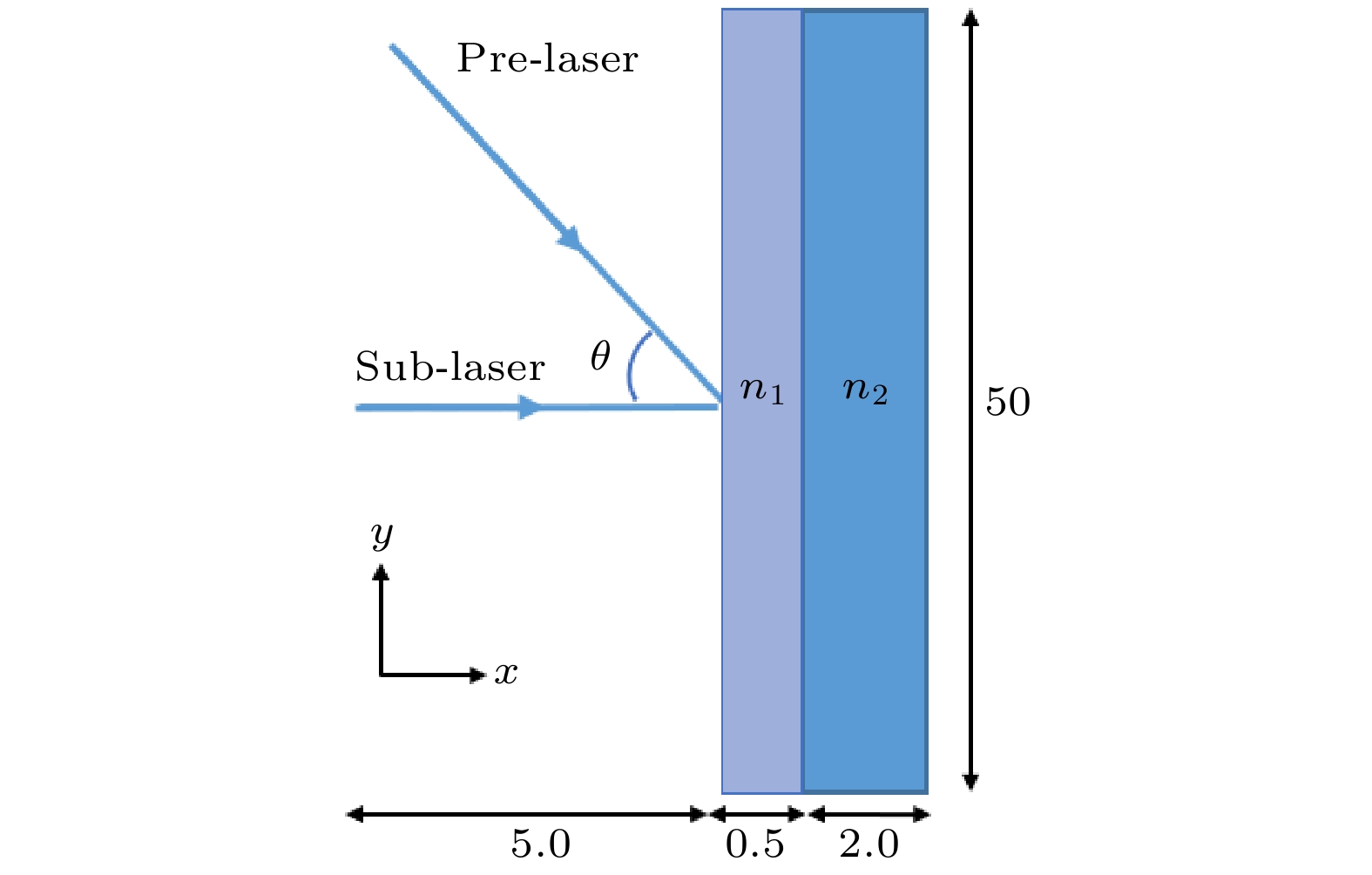
图 6 透射模拟设置示意图 (长度单位: μm, 密度n1
$\ll $ n2) ; 前置激光(pre-laser)以θ = 75°先入射等离子体靶, 在延迟Δt = 23T后正入射后续激光(sub-laser)Figure 6. Schematic diagram of transmission simulation settings (Length unit: μm, Density n1
$\ll $ n2 ); the pre-laser irradiates the plasma target at θ = 75°, and the subsequent laser (sub-laser) is normally incident after a delay of Δt = 23T).
图 7 (a) 单束激光正入射单层靶t = 30T时Ey(归一化)的分布, a =3, n = 100nc; (b) 两束激光先后射入双层等离子体靶t = 50T时Ey的分布, 前置激光a1 = 4, θ = 75°, 后续激光a2 = 3, θ = 0°, 延迟时间23T, 低密度层n1 = 2nc, 高密度层, n2 = 100nc. 为了使图(b) 中靶后电场更明显, 将强度绝对值超过1的电场都调整为1或 –1
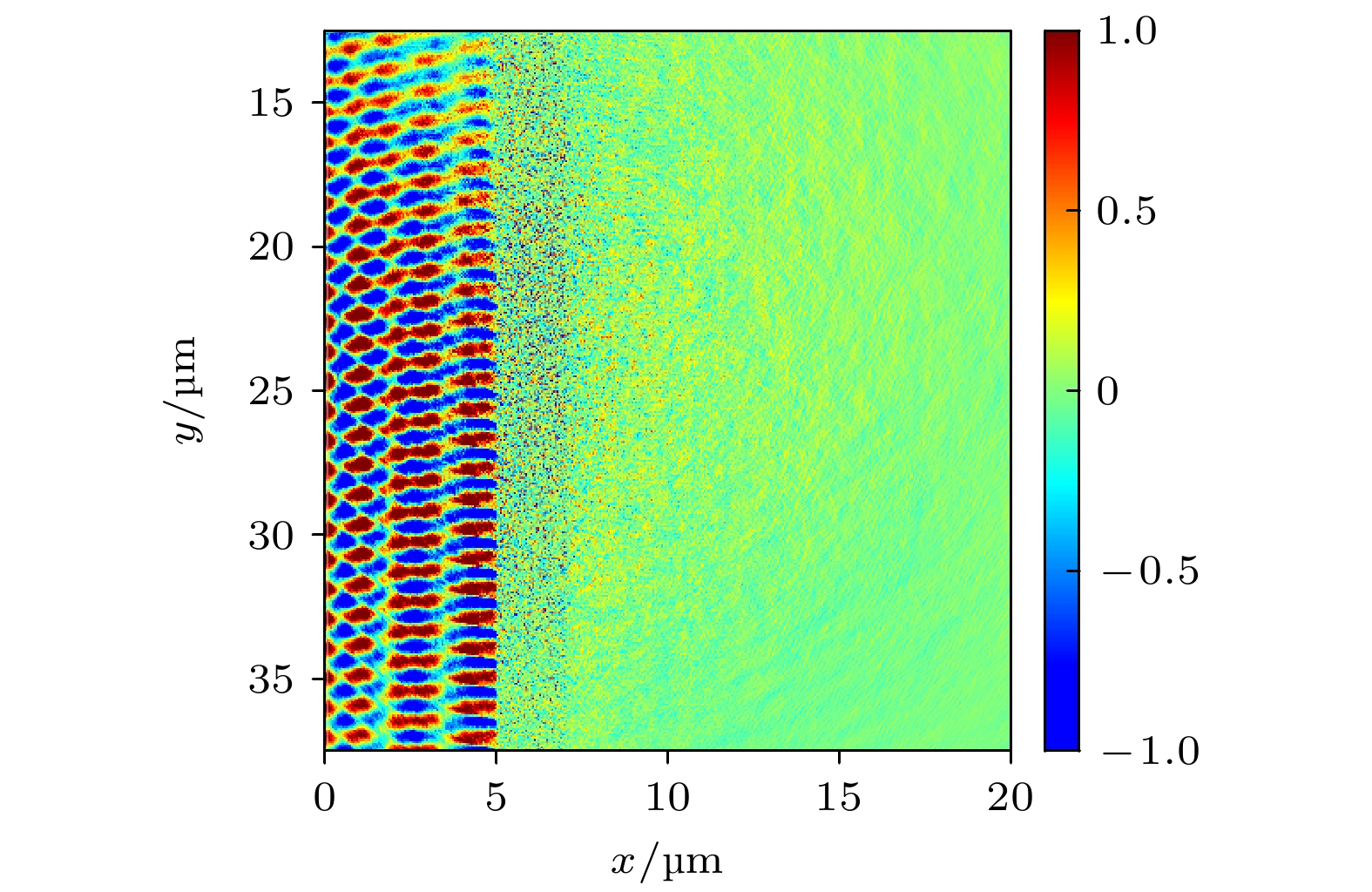
Figure 7. (a) The distribution of Ey (normalized) when a single laser beam is normally incident on a single-layer target, t = 30T, a = 3, n = 100nc; (b) the distribution of Ey when two laser beams successively shoot the double-layer plasma target, t = 50T, the pre-laser a1= 4, θ = 75 °, subsequent laser a2=3, θ = 0°, delay time 23T, low density layer n1 = 2nc; high density layer n2 = 100nc. In order to make the electric field behind the target in Figue (b) more obvious, if the absolute intensity of Ey is more than 1, adjust the electric field to 1 or –1.
图 8 (a) 激光主轴上电场的空间分布, 红线: 单束激光正入射单层靶, 蓝线: 两束激光先后入射双层靶; (b) 靶后即x > 7 μm的电场经傅里叶变换转换到幅度-波数域的结果, k0是入射光波数
Figure 8. (a) The spatial distribution of electric field on the main axis of laser. The red line: a single laser normally incident on a single-layer target, and the blue line: two laser beams successively incident on a double-layer target; (b) behind the target, x >7 μm, the result of electric field converted to the amplitude wavenumber domain by Fourier transform, k0 is the incident light wavenumber.
图 9 两束激光先后入射单层靶t = 50T时Ey (归一化)的分布
Figure 9. The distribution of Ey (normalized) when two laser beams successively incident on single-layer target, t = 50T.
-
[1] Otto A 1968 Z. Physik 216 398
Google Scholar
[2] Raether H 1988 Surface Plasmons on Smooth and Rough Surfaces and on Gratings (Springer
Google Scholar
[3] Ebbesen T W, Lezec H J, Ghaemi H F, Thio T, Wolff P A 1998 Nature 391 667
Google Scholar
[4] Liu H T, Lalanne P 2008 Nature 452 0672
Google Scholar
[5] Garcia-Vidal F J, Martin-Moreno L, Ebbesen T W 2010 Rev. Mod. Phys. 82 729
Google Scholar
[6] Florian C, Kirner S V, Kruger J, Bonse J 2020 J. Laser Appl. 32 022063
Google Scholar
[7] Ceccotti T, Floquet V, Sgattoni A, et al. 2013 Phys. Rev. Lett. 111 185001
Google Scholar
[8] Clark E L, Krushelnick K, Davies J R, et al. 2006 Phys. Plasma 96 670
Google Scholar
[9] Wilks S C, Langdon A B, Cowan T E, et al. 2001 Phys. Plasmas 8 542
Google Scholar
[10] Xu H, Yu W, Lu P X, Senecha V K, He F, Shen B F, Qian L J, Li R X, Xu Z Z 2005 Phys. Plasmas 12 013105
Google Scholar
[11] Chen L M, Kando M, Xu M H, et al. 2008 Phys. Rev. Lett. 100 045004
Google Scholar
[12] Dobosz S, Doumy G, Stabile H, D’Oliveira P, Monot P, Réau F, Hüller S, Martin Ph 2005 Phys. Rev. Lett. 95 025001
Google Scholar
[13] Zhu X M, Prasad1 R, Swantusch1 M, Aurand B, Andreev A A, Willi1 O, Cerchez M 2020 High Power Laser Sci. Eng. 8 e15
Google Scholar
[14] Marini S, Kleij P S, Amiranoff F, Grech M, Raynaud M 2021 Phys. Plasmas 28 073104
Google Scholar
[15] 胡希伟 2003 等离子体理论基础 (第二版) (北京: 北京大学出版社) 第270页
Hu X W 2003 Theoretical foundation of plasma (Vol. 2) (Beijing: Peking University Press) p270 (in Chinese)
[16] Rulliere C 2007 Femtosecond Laser Pulse Principles and Experiments (2nd Ed.) (Beijing: Science Press)
[17] Liu C S, Tripath V K, Shao X, Liu T C 2015 Phys. Plasma 22 412
Google Scholar
[18] Haider M M, Sheng Z M 2021 AIP Adv. 11 035221
Google Scholar
[19] Dawson J M 1962 Phys. Fluids 5 445
Google Scholar
[20] 张智猛 2011 博士学位论文 (杭州: 浙江大学)
Zhang Z M 2011 Ph. D. Dissertation (Hangzhou: Zhejiang University) (in Chinese)
[21] Zhang Z M, He X T, Sheng Z M, Yu M Y 2010 Phys. Plasma 17 043110
Google Scholar
[22] Zhang Z M, He X T, Sheng Z M, Yu M Y 2011 Phys. Plasma 18 023110
Google Scholar
[23] Sheng Z M, Zhu L W, Yu M Y, Zhang Z M 2010 New J. Phys. 12 013001
Google Scholar
[24] Birdsall C K, Fuss D 1969 Comput. Phys. 3 494
Google Scholar
[25] Yee K S 1966 IEEE Trans. Antennas Propag. 14 302
Google Scholar
[26] Fan G X, Liu Q H 1998 Wiley Subscription Services, Inc. A Wiley Company 19 258
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3538
- PDF Downloads: 78
- Cited By: 0
