Analysis and implementation of simple  four-dimensional memristive chaotic system with infinite coexisting attractors

Qin Ming-Hong; Lai Qiang; Wu Yong-Hong

doi:10.7498/aps.71.20220593

Abstract

Using memristors to construct special chaotic systems is highly interesting and meaningful. A simple four-dimensional memristive chaotic system with an infinite number of coexisting attractors is proposed in this paper, which has a relatively simple form but demonstrates complex dynamical behavior. Here, we use digital simulations to further investigate the system and utilize the bifurcation diagrams to describe the evolution of the dynamical behavior of the system with the influence of parameters. We find that the system can generate an abundance of chaotic and periodic attractors under different parameters. The amplitudes of the oscillations of the state variables of the system are closely dependent on the initial values. In addition, the experimental results of the circuit are consistent with the digital simulations, proving the existence and feasibility of this memristive chaotic system.

Keywords:

Authors and contacts

1.
ECJTU Tianyou College, East China Jiaotong University, Nanchang 330013, China
2.
School of Electrical and Automation Engineering, East China Jiaotong University, Nanchang 330013, China
3.
School of Science, Wuhan University of Technology, Wuhan 430074, China

Corresponding author: Lai Qiang, laiqiang87@126.com

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 61961019), the Natural Science Foundation of Jiangxi Province, China (Grant No. 20202ACBL212003), and the Natural Science Foundation of Hubei Province, China (Grant No. 2020CFB546).

FullText HTML : translate this paragraph

References

[1]	Chua L O 1971 IEEE Trans. Circuits Theor. 18 507 Google Scholar
[2]	Li C B, Sprott J C 2014 Int. J. Bifurcation Chaos 24 1450131 Google Scholar
[3]	鲜永菊, 夏诚, 钟德, 徐昌彪 2019 控制理论与应用 36 262 Google Scholar Xian Y J, Xia C, Zhong D, Xu C B 2019 Control Theory Appl. 36 262 Google Scholar
[4]	Li C B, Lu T N, Chen G R, Xing H Y 2019 Chaos 29 051102 Google Scholar
[5]	Lai Q, Wan Z Q, Kuate P D K 2020 Electron. Lett. 56 1044 Google Scholar
[6]	颜闽秀, 徐辉 2021 计算物理 38 244 Google Scholar Yan M X, Xu H 2021 Chin. J. Comput. Phys. 38 244 Google Scholar
[7]	Lai Q, Kuate P D K, Liu F, Liu F, Iu H H C 2019 IEEE Trans. Circuits Syst. Express Briefs 67 1129 Google Scholar
[8]	Lai Q 2021 Int. J. Bifurcation Chaos 31 2150013 Google Scholar
[9]	耿睿, 李中奇, 杨辉 2021 华东交通大学学报 38 61 Google Scholar Geng R, Li Z Q, Yang H 2021 J. East China Jiaotong Univ. 38 61 Google Scholar
[10]	Strukov D B, Snider G S, Stewart D R, Williams R S 2008 Nature 453 80 Google Scholar
[11]	Itoh M, Chua L O 2008 Int. J. Bifurcation Chaos 18 3183 Google Scholar
[12]	Muthuswamy B, Kokate P P 2009 IETE Tech. Rev. 26 417 Google Scholar
[13]	Li Z J, Zeng Y C 2013 Chin. Phys. B 22 040502 Google Scholar
[14]	Wang C H, Liu X M, Xia H 2017 Chaos 27 033114 Google Scholar
[15]	Lai Q, Wan Z Q, Kengne L K, Kuate P D K, Chen C Y 2020 IEEE Trans. Circuits Syst. Express Briefs 68 2197 Google Scholar
[16]	李晓霞, 郑驰, 王雪, 曹樱子, 徐桂芝 2022 哈尔滨工业大学学报 54 163 Google Scholar Li X X, Zheng C, Wang X, Cao Y Z, Xu G Z 2022 J. Harbin Eng. Univ. 54 163 Google Scholar
[17]	Lai Q, Lai C, Kuate P D K, Li C B, He S B 2022 Int. J. Bifurcation Chaos 32 2250042 Google Scholar
[18]	Lai Q, Wan Z Q, Zhang H, Chen G R 2022 IEEE Trans. Neural Networks Learn. Syst.Google Scholar
[19]	Lai Q, Lai C, Zhang H, Li C B 2022 Chaos, Solitons Fractals 158 112017 Google Scholar
[20]	包伯成, 胡文, 许建平, 刘中, 邹凌 2011 60 120502 Google Scholar Bao B C, Hu W, Xu J P, Liu Z, Zou L 2011 Acta Phys. Sin. 60 120502 Google Scholar
[21]	Li C B, Sprott J C 2016 Optik 127 10389 Google Scholar
[22]	孙佳钰 2021 硕士学位论文 (南京: 南京信息工程大学) Sun J Y 2021 M. S. Thesis (Nanjing: Nanjing University of Information Science and Technology) (in Chinese)
[23]	Huang L L, Wang Y L, Jiang Y C, Lei T F 2021 Math. Prob. Eng. 2021 7457220 Google Scholar
[24]	Zhang X, Li C B, Chen Y D, Iu H H C Lei T F 2020 Chaos, Solitons Fractals 139 110000 Google Scholar
[25]	Carr J 1981 Applications of Centre Manifold Theory (New York: Springer) pp1–50
[26]	史传宝, 王光义, 臧寿池 2017 杭州电子科技大学学报(自然科学版) 37 1 Google Scholar Shi C B, Wang G Y, Zang S C 2017 J. Hangzhou Dianzi Univ. (Nat. Sci. ) 37 1 Google Scholar
[27]	王伟, 曾以成, 陈争, 孙睿婷 2017 计算物理 34 747 Google Scholar Wang W, Zeng Y C, Chen Z, Sun R T 2017 Chin. J. Comput. Phys. 34 747 Google Scholar

Cited By

图 1 原系统(2)电路原理图及忆阻输出反馈控制电路图

Figure 1. Circuit schematic of the original system (2) and circuit diagram of the memristor output feedback control term.

DownLoad: Full-Size Img PowerPoint

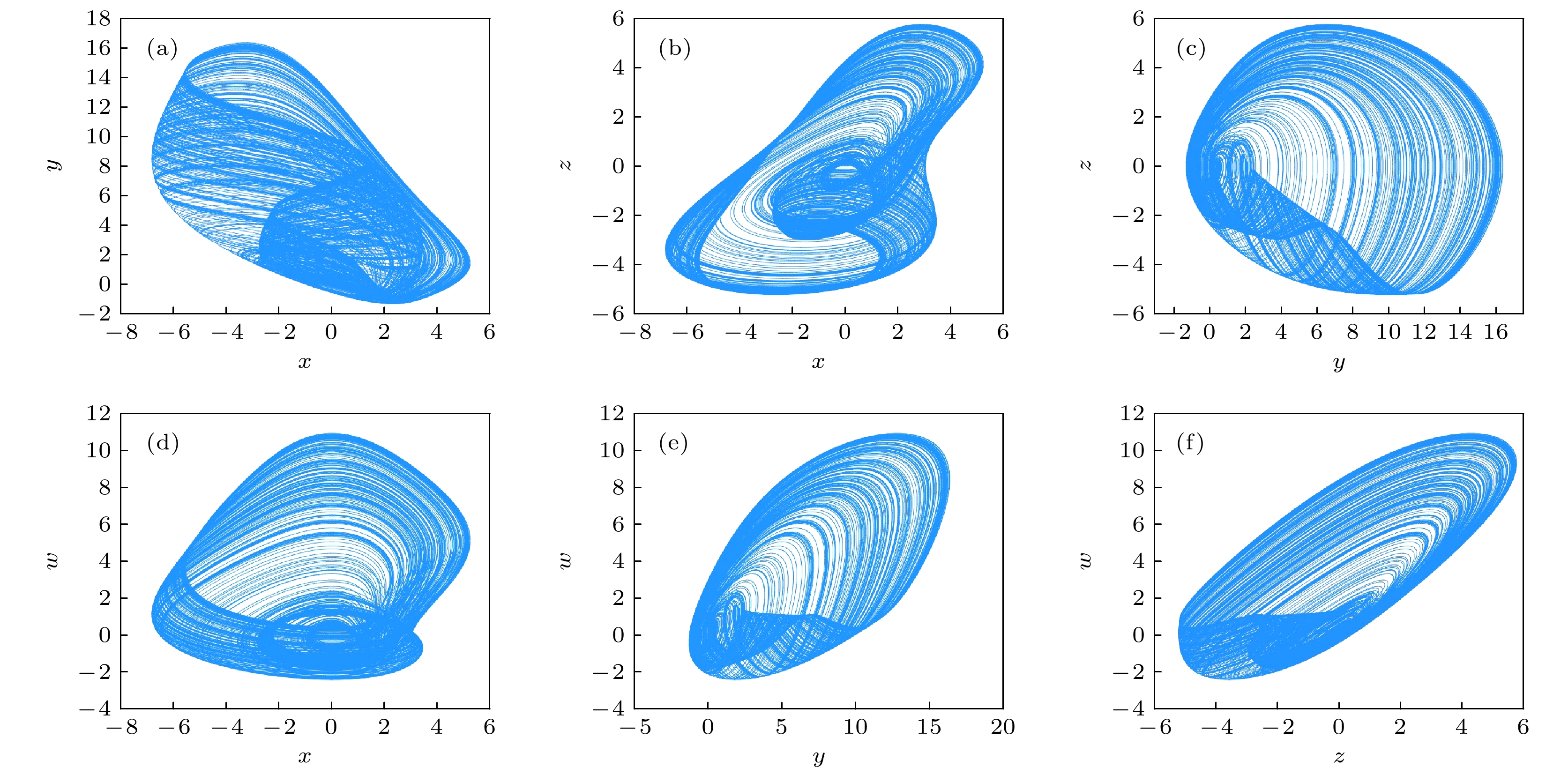
图 2 参数$ a=1.6, b=0.5, p=0.2, q=0.1 $和初值$ [0.1, 0.1, 0.2, 0.5] $时系统的相平面图　(a)$ x \text- y $平面; (b)$ x\text- z $平面; (c)$ y \text- z $平面; (d)$ x \text- w $平面; (e)$ y \text- w $平面; (f)$ z \text- w $平面

Figure 2. Phase portraits of the system with parameters $ a = 1.6, {\text{ }}b = 0.5, {\text{ }}p = 0.2, {\text{ }}q = 0.1 $ and initial values $ [0.1, 0.1, 0.2, 0.5] $: (a)$ x \text- y $ plane; (b)$ x \text- z $ plane; (c)$ y \text- z $ plane; (d)$ x \text- w $ plane; (e)$ y \text- w $ plane; (f)$ z \text- w $ plane.

DownLoad: Full-Size Img PowerPoint

图 3 参数$ b = 0.5, {\text{ }}p = 0.2, {\text{ }}q = 0.1 $和初值$ [0.1, 0.1, 0.2, 0.5] $时系统随参数$ a \in [0, 10] $的分岔图(a)与Lyapunov指数谱(b)

Figure 3. Bifurcation diagram (a) and Lyapunov exponent spectrum (b) for system parameters$ a \in [0, 10] $ with$b = 0.5, {\text{ }}p = 0.2, $$ {\text{ }}q = 0.1$ and initial values of $ [0.1, 0.1, 0.2, 0.5] $.

DownLoad: Full-Size Img PowerPoint

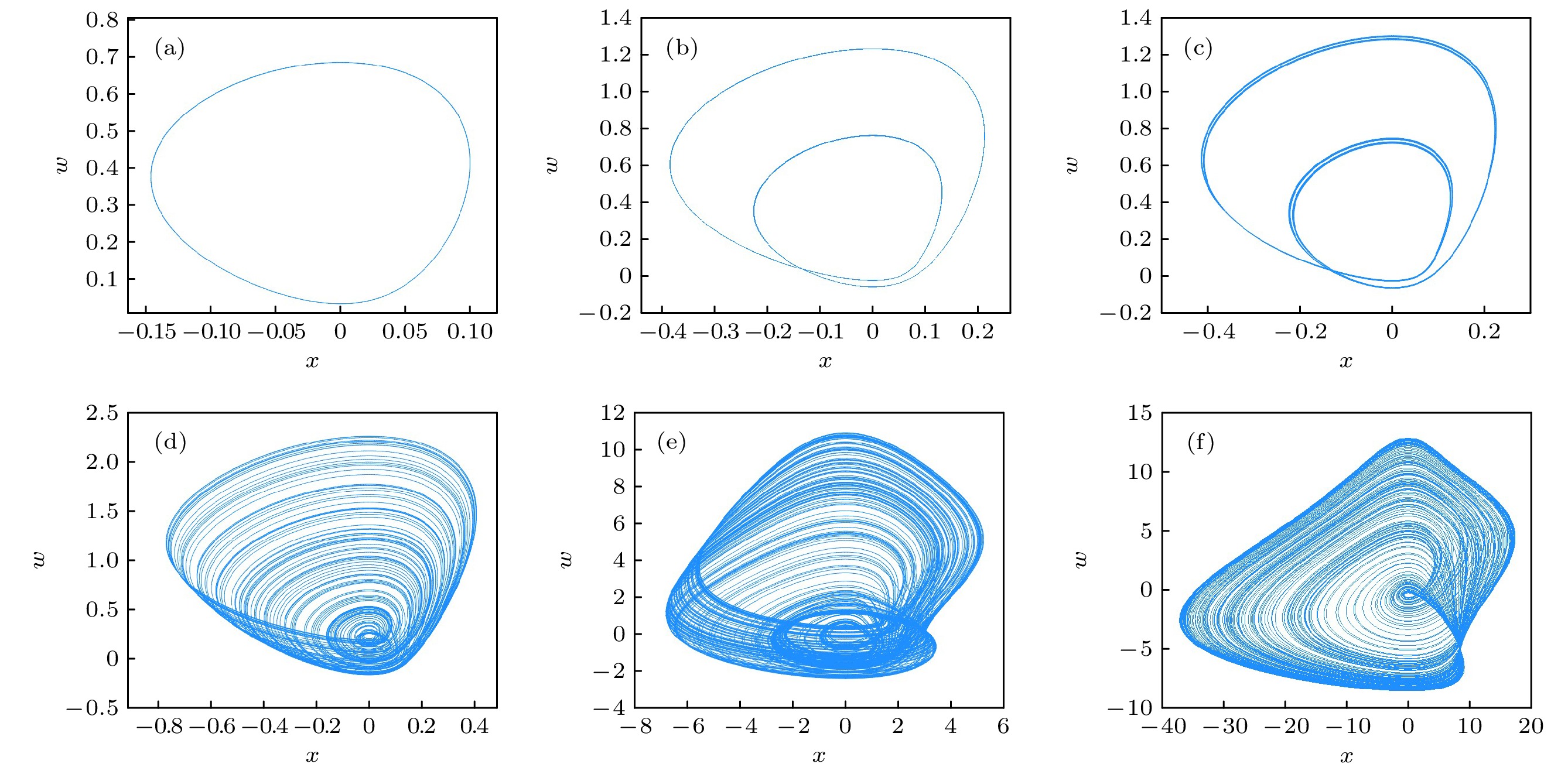
图 4 系统参数为$ b = 0.5, {\text{ }}p = 0.2, {\text{ }}q = 0.1 $, 初值为$ [0.1, 0.1, 0.2, 0.5] $时, 表2中不同$ a $值对应的$x \text- w$相平面图　(a) a = 0.1; (b) a = 0.15; (c) a = 0.155; (d) a = 0.2; (e) a = 1.6; (f) a = 9.1

Figure 4. $x \text- w$ phase plane diagrams corresponding to different $ a $ values in Table 2 for system parameter $ b = 0.5, {\text{ }}p = 0.2, {\text{ }}q = 0.1 $ and an initial value of $ [0.1, 0.1, 0.2, 0.5] $: (a) a = 0.1; (b) a = 0.15; (c) a = 0.155; (d) a = 0.2; (e) a = 1.6; (f) a = 9.1.

DownLoad: Full-Size Img PowerPoint

图 5 系统参数为$a \;=\; 1.6, {\text{ }}b\; =\; 0.5, {\text{ }}q\; =\; 0.1$, 初值为$ [0.1, 0.1, 0.2, 0.5] $时, 系统参数$ p \in (0, 0.52] $的分岔图(a)与Lyapunov指数谱(b)

Figure 5. Bifurcation diagram (a) with Lyapunov exponent spectrum (b) for system parameters$ p \in (0, 0.52] $ for $a = 1.6, {\text{ }}b = 0.5, $$ {\text{ }}q = 0.1$ and initial values of $ [0.1, 0.1, 0.2, 0.5] $.

DownLoad: Full-Size Img PowerPoint

图 6 系统参数为$ a = 1.6, {\text{ }}b = 0.5, {\text{ }}p = 0.2 $, 初值为$ [0.1, 0.1, 0.2, 0.5] $时, 系统参数$ q \in [0.1, 0.16] $的分岔图(a)与Lyapunov指数谱(b)

Figure 6. Bifurcation diagram (a) with Lyapunov exponent spectrum (b) for system parameters $ q \in [0.1, 0.16] $ with $a = 1.6, $$ {\text{ }}b = 0.5, {\text{ }}p = 0.2$and initial values of $ [0.1, 0.1, 0.2, 0.5] $.

DownLoad: Full-Size Img PowerPoint

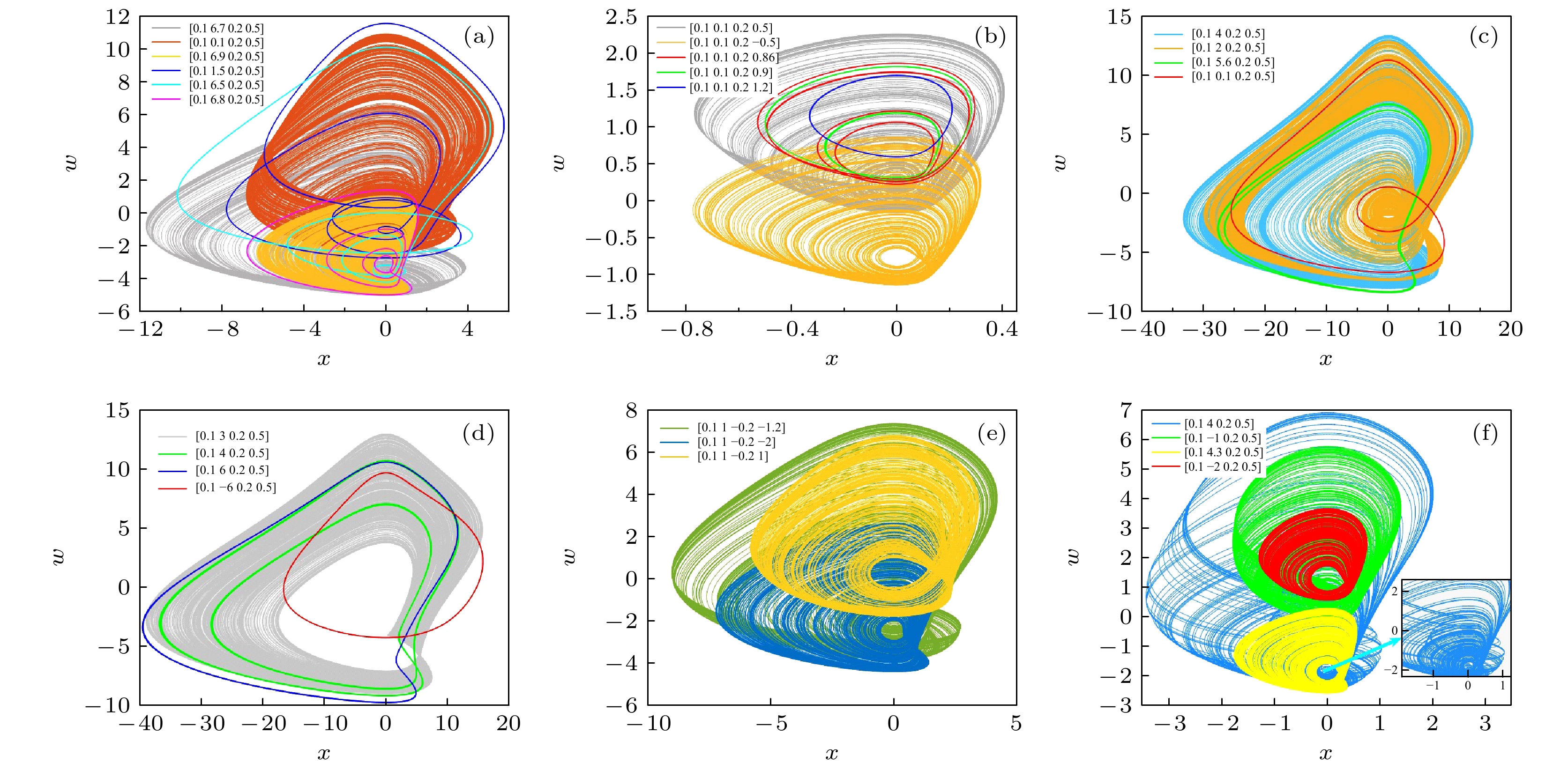
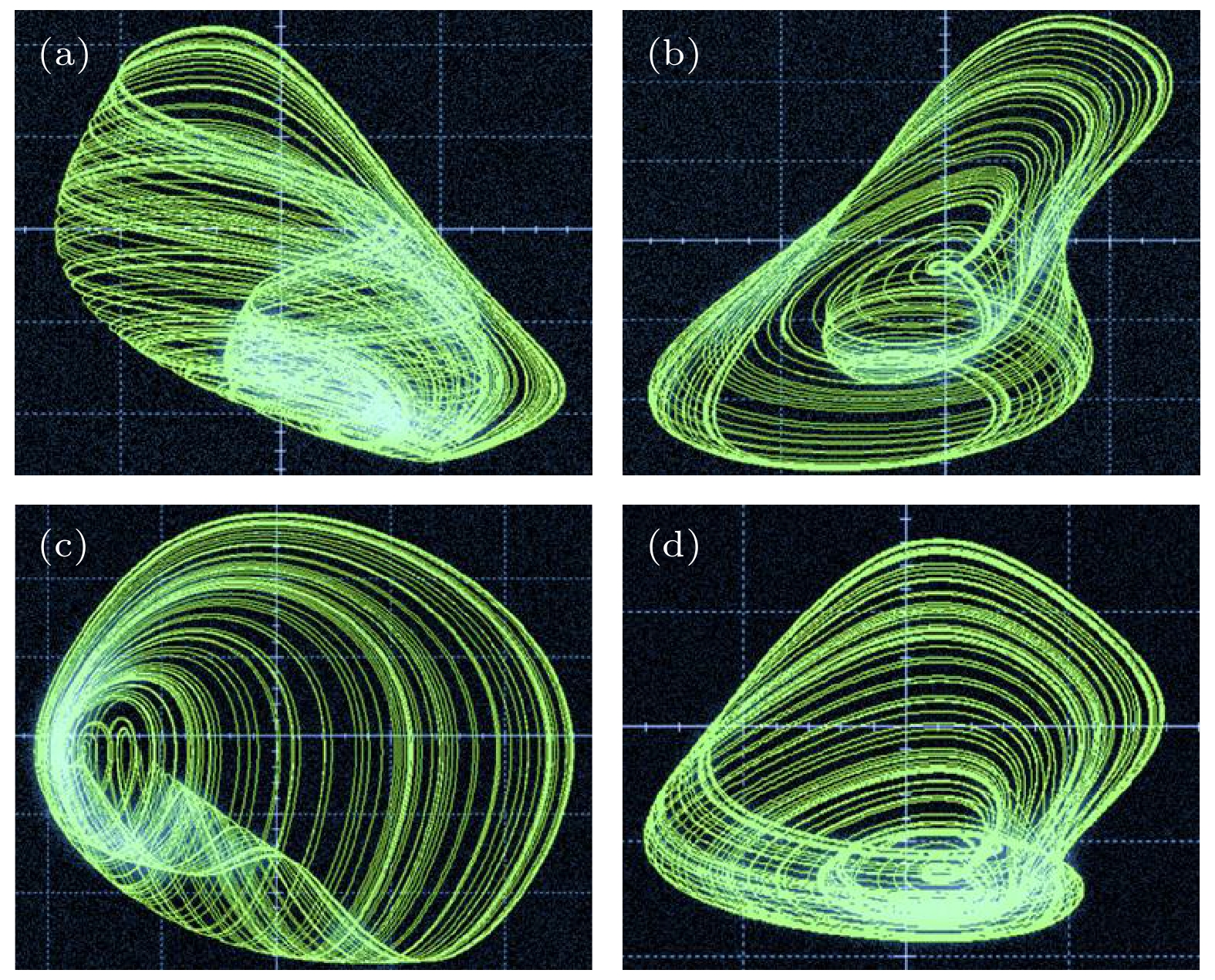
图 7 表3中的不同系统参数下的共存吸引子的$x {\text{-}} w$相平面图　(a) a = 1.6, b = 0.5, p = 0.2, q = 0.1; (b) a = 0.2, b = 0.5, p = 0.2, q = 0.1; (c) a = 6, b = 0.5, p = 0.2, q = 0.1; (d) a = 8, b = 0.5, p = 0.2, q = 0.1; (e) a = 2, b = 0.6, p = 0.5, q = 0.1; (f) a = 0.5, b = 0.5, p = 0.5, q = 0.1

Figure 7. $x {\text{-}} w$ phase plane plots of coexisting attractors for different system parameters in Table 3: (a) a = 1.6, b = 0.5, p = 0.2, q = 0.1; (b) a = 0.2, b = 0.5, p = 0.2, q = 0.1; (c) a = 6, b = 0.5, p = 0.2, q = 0.1; (d) a = 8, b = 0.5, p = 0.2, q = 0.1; (e) a = 2, b = 0.6, p = 0.5, q = 0.1; (f) a = 0.5, b = 0.5, p = 0.5, q = 0.1.

DownLoad: Full-Size Img PowerPoint

图 8 参数$a = 1.6, \;b = 0.5, \;p = 0.2, \;q = 0.1$时, 系统(3)在不同初始条件条件下的A, B系列多共存引子: (a)共存周期吸引子A₁—A₉; (b)共存混沌吸引子B₁—B₆

Figure 8. The system (3) with parameters $a = 1.6, \;b = 0.5, \;p = 0.2, \;q = 0.1$ has multiple coexisting chaotic attractors of series A and B under different initial conditions: (a) Coexisting periodic attractors A₁–A₉; (b) coexisting chaotic attractors B₁–B₆.

DownLoad: Full-Size Img PowerPoint

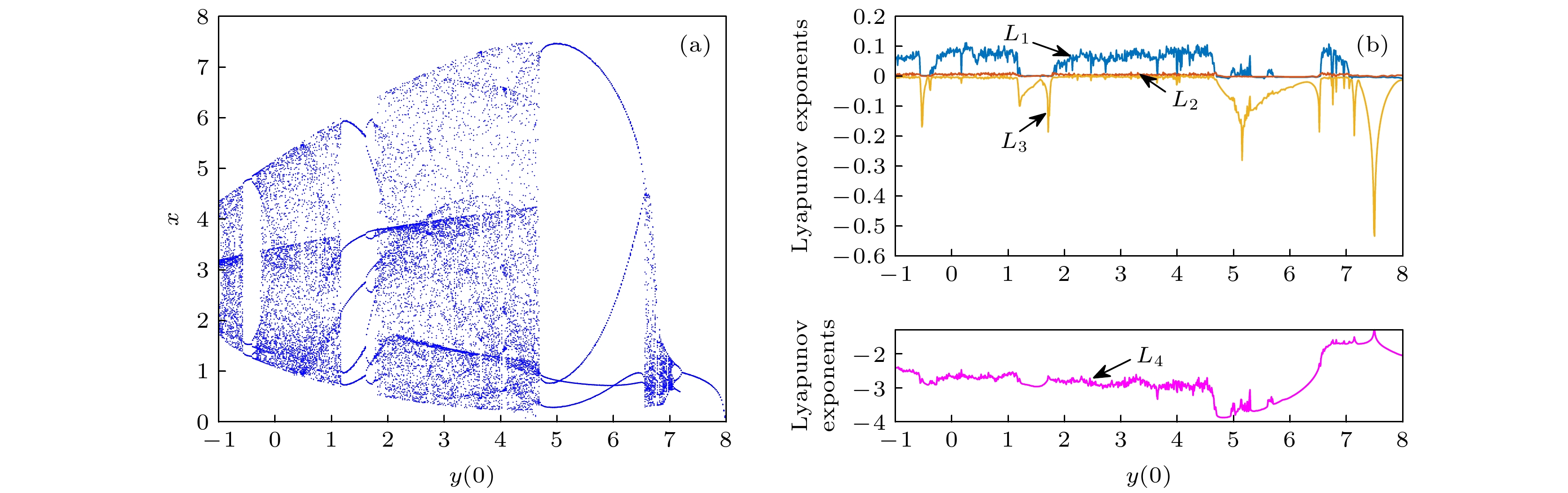
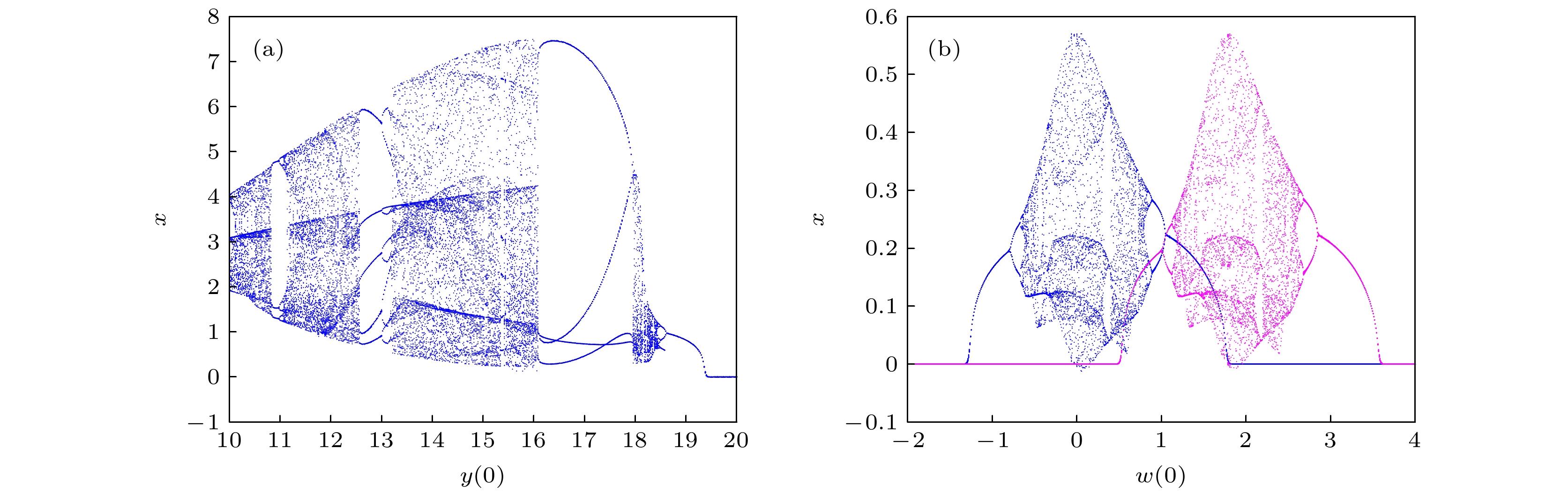
图 9 参数$ a = 1.6, {\text{ }}b = 0.5, {\text{ }}p = 0.2, {\text{ }}q = 0.1 $和初始值$ [0.1, y(0), 0.2, 0.5] $时, 系统(3)随初始值$ y(0) \in [ - 1, 8] $的分岔图(a)与Lyapunov指数谱(b)

Figure 9. Bifurcation diagram (a) of system (3) initial condition $ y(0) \in [ - 1, 8] $ for parameter $ a = 1.6, {\text{ }}b = 0.5, {\text{ }}p = 0.2, {\text{ }}q = 0.1 $ and initial value $ [0.1, y(0), 0.2, 0.5] $ with Lyapunov exponential spectrum (b).

DownLoad: Full-Size Img PowerPoint

图 10 系统(3)随初始值变化的分岔图　(a)参数$ a = 1.6, {\text{ }}b = 0.5, {\text{ }}p = 0.2, {\text{ }}q = 0.1 $且初值为$ [0.1, y(0), 1, 7] $时, 系统初始条件$ y(0) \in [10,20] $的分岔图; (b)参数为$ a = 0.2, {\text{ }}b = 0.5, {\text{ }}p = 0.2, {\text{ }}q = 0.1 $和初值为$ [0.1, 0.1, 0.2, w(0)] $(蓝色), $ [0.1, 0.1, 2, w(0)] $(紫色)时, 系统初始条件$ w(0) \in [ - 2, 4] $的分岔图

Figure 10. Bifurcation diagram of system (3) with initial values: (a) Bifurcation diagram of system initial condition $ y(0) \in [10,20] $ for parameter $ a = 1.6, {\text{ }}b = 0.5, {\text{ }}p = 0.2, {\text{ }}q = 0.1 $ with initial value $ [0.1, y(0), 1, 7] $; (b) bifurcation diagram of system initial condition $ w(0) \in [ - 2, 4] $ for parameter $ a = 0.2, {\text{ }}b = 0.5, {\text{ }}p = 0.2, {\text{ }}q = 0.1 $ and initial values $ [0.1, 0.1, 0.2, w(0)] $ (blue) and $ [0.1, 0.1, 2, w(0)] $ (purple).

DownLoad: Full-Size Img PowerPoint

图 11 忆阻系统电路原理图

Figure 11. Circuit schematic of the memristive chaotic system.

DownLoad: Full-Size Img PowerPoint

图 12 电路实验结果图 (a)—(d) 示波器中$ x - y $, $ x - z $, $ y - z $, $ x - w $相平面图

Figure 12. Plots of experimental results of the circuit: (a)–(d) the $ x - y $, $ x - z $, $ y - z $ and$ x - w $ phase planes in the oscilloscope respectively.

DownLoad: Full-Size Img PowerPoint

表 1 系统(3)与部分同类型系统的对比

Table 1. Comparison of system (3) with some systems of the same type.

系统	原系统编号	原系统中非线性项的个数	新系统的总项数	新系统中非线性项的个数	文献编号
系统A	VB2	1	6	4	[22]
系统B	VB18	2	7	5	[23]
系统C	VB5	3	8	8	[24]
本系统	VB3	1	7	2	—

DownLoad: CSV

表 2 系统参数为$ b = 0.5, p = 0.2, q = 0.1 $, 初值为$ [0.1, 0.1, 0.2, 0.5] $时, 不同$ a $值下吸引子类型及图像编号

Table 2. Attractor types and image numbers for different $ a $ values with system parameter$b = 0.5, p = 0.2, $$ q = 0.1$ and initial values $ [0.1, 0.1, 0.2, 0.5] $.

参数$ a $的取值	吸引子类型	图像编号
0.1	周期-1
0.15	周期–2	图4(a)—(c)
0.155	周期–4
0.2	混沌
1.6	混沌	图4(d)—图4(f)
9.1	混沌

DownLoad: CSV

表 3 不同系统参数下系统共存吸引子类型与图像编号

Table 3. Coexistence of attractor types and image numbers for different system parameters.

系统参数	初始值	吸引子类型	图像编号
a = 1.6, b = 0.5, p = 0.2, q = 0.1	[0.1 0.1 0.2 0.5], [0.1 6.7 0.2 0.5] [0.1 6.9 0.2 0.5], [0.1 1.5 0.2 0.5] [0.1 6.5 0.2 0.5], [0.1 6.8 0.2 0.5]	三个混沌吸引子与三个周期吸引子	图7(a)
a = 0.2, b = 0.5, p = 0.2, q = 0.1	[0.1 0.1 0.2 1.2], [0.1 0.1 0.2 –0.5] [0.1 0.1 0.2 0.86], [0.1 0.1 0.2 0.5] [0.1 0.1 0.2 0.9]	三个周期吸引子与两个混沌吸引子	图7(b)
a = 6, b = 0.5, p = 0.2, q = 0.1	[0.1 0.1 0.2 0.5], [0.1 5.6 0.2 0.5] [0.1 2 0.2 0.5], [0.1 4 0.2 0.5]	两个周期吸引子与两个混沌吸引子	图7(c)
a = 8, b = 0.5, p = 0.2, q = 0.1	[0.1 –6 0.2 0.5], [0.1 6 0.2 0.5] [0.1 4 0.2 0.5], [0.1 3 0.2 0.5]	三个周期吸引子与一个混沌吸引子	图7(d)
a = 2, b = 0.6, p = 0.5, q = 0.1	[0.1 1 –0.2 1], [0.1 1 –0.2 –2] [0.1 1 –0.2 –1.2]	三个混沌吸引子	图7(e)
a = 0.5, b = 0.5, p = 0.5, q = 0.1	[0.1, 4, 0.2, 0.5], [0.1, –1, 0.2, 0.5] [0.1, 4.3, 0.2, 0.5], [0.1, –2, 0.2, 0.5]	四个混沌吸引子	图7(f)

DownLoad: CSV

map

[1]	Chua L O 1971 IEEE Trans. Circuits Theor. 18 507 Google Scholar
[2]	Li C B, Sprott J C 2014 Int. J. Bifurcation Chaos 24 1450131 Google Scholar
[3]	鲜永菊, 夏诚, 钟德, 徐昌彪 2019 控制理论与应用 36 262 Google Scholar Xian Y J, Xia C, Zhong D, Xu C B 2019 Control Theory Appl. 36 262 Google Scholar
[4]	Li C B, Lu T N, Chen G R, Xing H Y 2019 Chaos 29 051102 Google Scholar
[5]	Lai Q, Wan Z Q, Kuate P D K 2020 Electron. Lett. 56 1044 Google Scholar
[6]	颜闽秀, 徐辉 2021 计算物理 38 244 Google Scholar Yan M X, Xu H 2021 Chin. J. Comput. Phys. 38 244 Google Scholar
[7]	Lai Q, Kuate P D K, Liu F, Liu F, Iu H H C 2019 IEEE Trans. Circuits Syst. Express Briefs 67 1129 Google Scholar
[8]	Lai Q 2021 Int. J. Bifurcation Chaos 31 2150013 Google Scholar
[9]	耿睿, 李中奇, 杨辉 2021 华东交通大学学报 38 61 Google Scholar Geng R, Li Z Q, Yang H 2021 J. East China Jiaotong Univ. 38 61 Google Scholar
[10]	Strukov D B, Snider G S, Stewart D R, Williams R S 2008 Nature 453 80 Google Scholar
[11]	Itoh M, Chua L O 2008 Int. J. Bifurcation Chaos 18 3183 Google Scholar
[12]	Muthuswamy B, Kokate P P 2009 IETE Tech. Rev. 26 417 Google Scholar
[13]	Li Z J, Zeng Y C 2013 Chin. Phys. B 22 040502 Google Scholar
[14]	Wang C H, Liu X M, Xia H 2017 Chaos 27 033114 Google Scholar
[15]	Lai Q, Wan Z Q, Kengne L K, Kuate P D K, Chen C Y 2020 IEEE Trans. Circuits Syst. Express Briefs 68 2197 Google Scholar
[16]	李晓霞, 郑驰, 王雪, 曹樱子, 徐桂芝 2022 哈尔滨工业大学学报 54 163 Google Scholar Li X X, Zheng C, Wang X, Cao Y Z, Xu G Z 2022 J. Harbin Eng. Univ. 54 163 Google Scholar
[17]	Lai Q, Lai C, Kuate P D K, Li C B, He S B 2022 Int. J. Bifurcation Chaos 32 2250042 Google Scholar
[18]	Lai Q, Wan Z Q, Zhang H, Chen G R 2022 IEEE Trans. Neural Networks Learn. Syst.Google Scholar
[19]	Lai Q, Lai C, Zhang H, Li C B 2022 Chaos, Solitons Fractals 158 112017 Google Scholar
[20]	包伯成, 胡文, 许建平, 刘中, 邹凌 2011 60 120502 Google Scholar Bao B C, Hu W, Xu J P, Liu Z, Zou L 2011 Acta Phys. Sin. 60 120502 Google Scholar
[21]	Li C B, Sprott J C 2016 Optik 127 10389 Google Scholar
[22]	孙佳钰 2021 硕士学位论文 (南京: 南京信息工程大学) Sun J Y 2021 M. S. Thesis (Nanjing: Nanjing University of Information Science and Technology) (in Chinese)
[23]	Huang L L, Wang Y L, Jiang Y C, Lei T F 2021 Math. Prob. Eng. 2021 7457220 Google Scholar
[24]	Zhang X, Li C B, Chen Y D, Iu H H C Lei T F 2020 Chaos, Solitons Fractals 139 110000 Google Scholar
[25]	Carr J 1981 Applications of Centre Manifold Theory (New York: Springer) pp1–50
[26]	史传宝, 王光义, 臧寿池 2017 杭州电子科技大学学报(自然科学版) 37 1 Google Scholar Shi C B, Wang G Y, Zang S C 2017 J. Hangzhou Dianzi Univ. (Nat. Sci. ) 37 1 Google Scholar
[27]	王伟, 曾以成, 陈争, 孙睿婷 2017 计算物理 34 747 Google Scholar Wang W, Zeng Y C, Chen Z, Sun R T 2017 Chin. J. Comput. Phys. 34 747 Google Scholar

[1]	Fu Long-Xiang, He Shao-Bo, Wang Hui-Hai, Sun Ke-Hui. Simulink modeling and dynamic characteristics of discrete memristor chaotic system. Acta Physica Sinica, 2022, 71(3): 030501. doi: 10.7498/aps.71.20211549
[2]	Zhang Gui-Zhong, Quan Xu, Liu Song. Analysis and FPGA implementation of memristor chaotic system with extreme multistability. Acta Physica Sinica, 2022, 71(24): 240502. doi: 10.7498/aps.71.20221423
[3]	. Simulink Modeling and Dynamics of a Discrete Memristor Chaotic System. Acta Physica Sinica, 2021, (): . doi: 10.7498/aps.70.20211549
[4]	Xiao Li-Quan, Duan Shu-Kai, Wang Li-Dan. Julia fractal based multi-scroll memristive chaotic system. Acta Physica Sinica, 2018, 67(9): 090502. doi: 10.7498/aps.67.20172761
[5]	Bao Han, Bao Bo-Cheng, Lin Yi, Wang Jiang, Wu Hua-Gan. Hidden attractor and its dynamical characteristic in memristive self-oscillating system. Acta Physica Sinica, 2016, 65(18): 180501. doi: 10.7498/aps.65.180501
[6]	Wu Xian-Ming, He Yi-Gang, Yu Wen-Xin. Design and implementation of grid multi-scroll chaotic circuit based on current feedback operational amplifier. Acta Physica Sinica, 2014, 63(18): 180506. doi: 10.7498/aps.63.180506
[7]	Huang Yun. A family of multi-wing chaotic attractors and its circuit implementation. Acta Physica Sinica, 2014, 63(8): 080505. doi: 10.7498/aps.63.080505
[8]	Jia Hong-Yan, Chen Zeng-Qiang, Xue Wei. Analysis and circuit implementation for the fractional-order Lorenz system. Acta Physica Sinica, 2013, 62(14): 140503. doi: 10.7498/aps.62.140503
[9]	Luo Ming-Wei, Luo Xiao-Hua, Li Hua-Qing. A family of four-dimensional multi-wing chaotic system and its circuit implementation. Acta Physica Sinica, 2013, 62(2): 020512. doi: 10.7498/aps.62.020512
[10]	Wang Chun-Hua, Yin Jin-Wen, Lin Yuan. Design and realization of grid multi-scroll chaotic circuit based on current conveyers. Acta Physica Sinica, 2012, 61(21): 210507. doi: 10.7498/aps.61.210507
[11]	Huang Li-Lian, Xin Fang, Wang Lin-Yu. Circuit implementation and control of a new fractional-order hyperchaotic system. Acta Physica Sinica, 2011, 60(1): 010505. doi: 10.7498/aps.60.010505
[12]	Liu Zhong, Wu Hua-Gan, Bao Bo-Cheng. Scroll number and distribution control of attractor: system design and circuit realization. Acta Physica Sinica, 2011, 60(9): 090502. doi: 10.7498/aps.60.090502
[13]	Chen Shi-Bi, Zeng Yi-Cheng, Xu Mao-Lin, Chen Jia-Sheng. Construction of grid multi-scroll chaotic attractors and its circuit implementation with polynomial and step function. Acta Physica Sinica, 2011, 60(2): 020507. doi: 10.7498/aps.60.020507
[14]	Li Chun-Biao, Wang Han-Kang, Chen Su. A novel chaotic attractor with constant Lyapunov exponent spectrum and its circuit implementation. Acta Physica Sinica, 2010, 59(2): 783-791. doi: 10.7498/aps.59.783
[15]	Xue Wei, Guo Yan-Ling, Chen Zeng-Qiang. Analysis of chaos and circuit implementation of a permanent magnet synchronous motor. Acta Physica Sinica, 2009, 58(12): 8146-8151. doi: 10.7498/aps.58.8146
[16]	Zheng Gui-Bo, Jin Ning-De. Multiscale entropy and dynamic characteristics of two-phase flow patterns. Acta Physica Sinica, 2009, 58(7): 4485-4492. doi: 10.7498/aps.58.4485
[17]	Liu Yang-Zheng. A new hyperchaotic Lü system and its circuit realization. Acta Physica Sinica, 2008, 57(3): 1439-1443. doi: 10.7498/aps.57.1439
[18]	Wang Guang-Yi, Zheng Yan, Liu Jing-Biao. A hyperchaotic Lorenz attractor and its circuit implementation. Acta Physica Sinica, 2007, 56(6): 3113-3120. doi: 10.7498/aps.56.3113
[19]	Cai Guo-Liang, Tan Zhen-Mei, Zhou Wei-Huai, Tu Wen-Tao. Dynamical analysis of a new chaotic system and its chaotic control. Acta Physica Sinica, 2007, 56(11): 6230-6237. doi: 10.7498/aps.56.6230
[20]	Li Shi-Hua, Cai Hai-Xing. Research on circuitry realization and synchronization of Chen chaotic systems. Acta Physica Sinica, 2004, 53(6): 1687-1693. doi: 10.7498/aps.53.1687

Catalog

Vol. 71, Issue 16 - 2022-08-20

Metrics

Abstract views: 5053
PDF Downloads: 175
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板