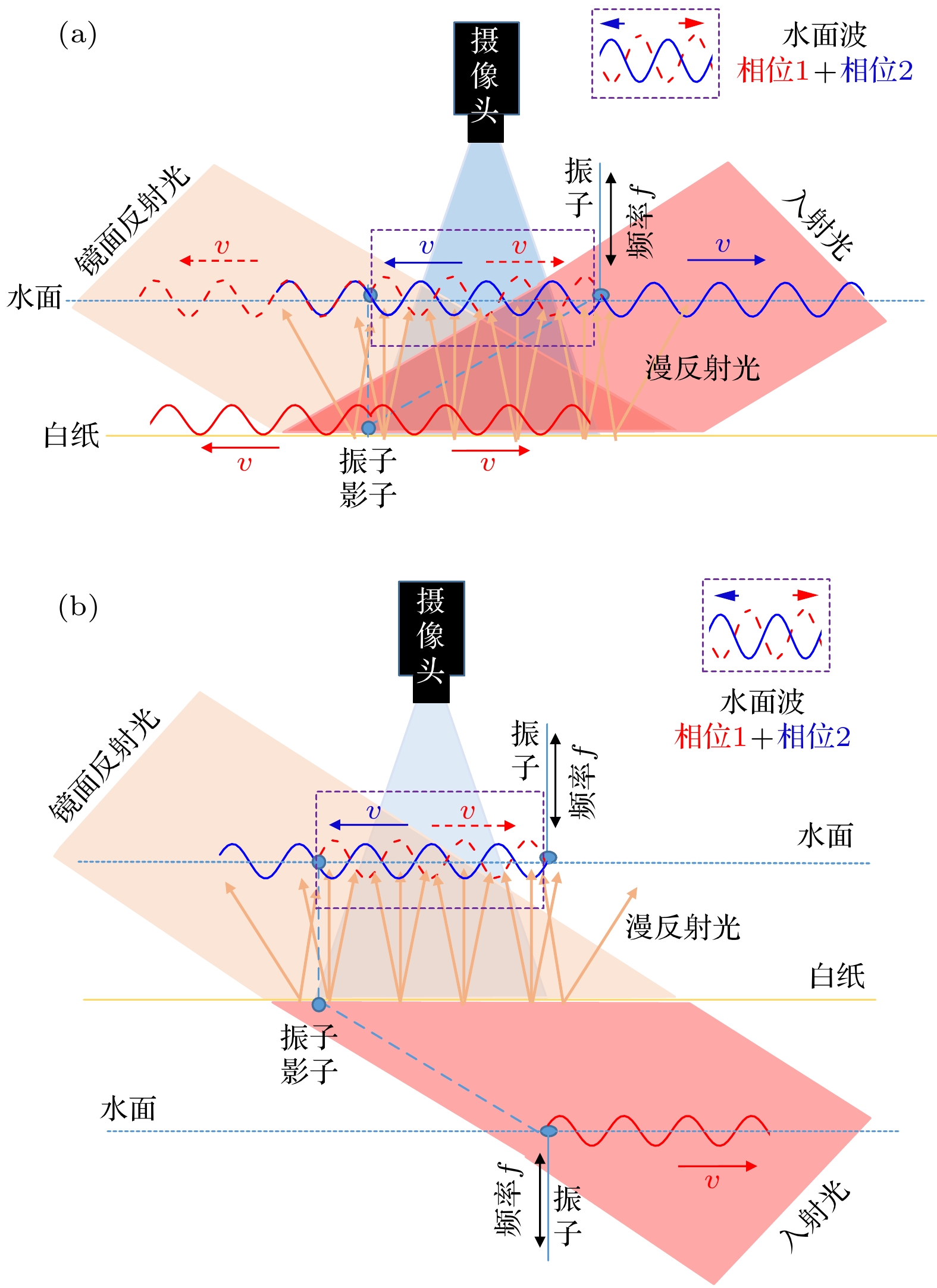
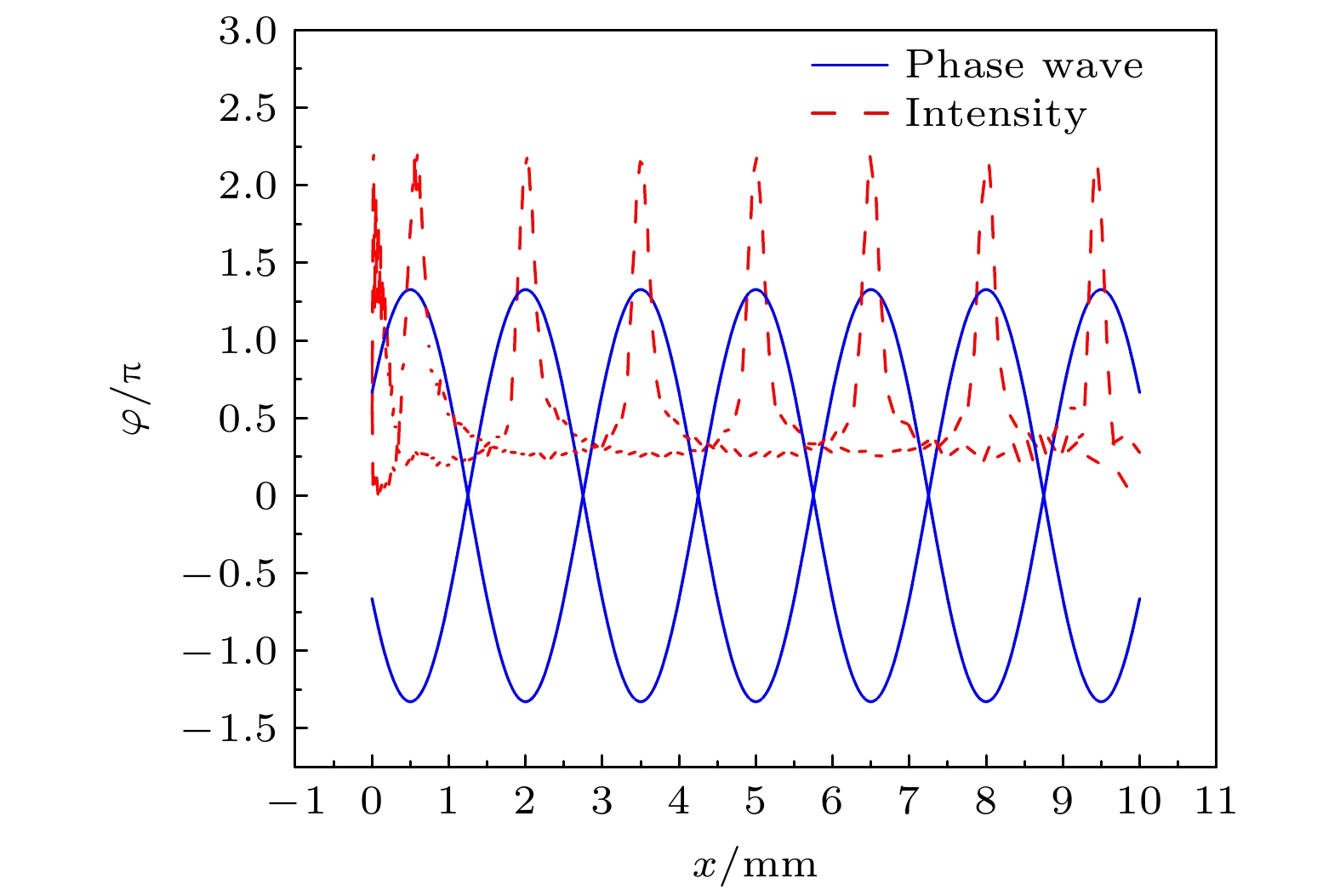
-
The surface tension of liquid is an important parameter to characterize the properties of liquid. The non-contact method of measuring the surface tension coefficient of liquid has the advantages of being fast, non-destructive, simple and practical. A new non-contact method of measuring the surface tension coefficient of transparent liquid based on the theory of light propagation is developed, and a special phenomenon of “self-interference” is discovered. The “Phase Standing Wave” theory is proposed to explain the phenomenon. The surface wave of the liquid is excited by a frequency-adjustable vibration source (oscillator), and it propagates dynamically in the form of oscillator and cosine wave. When the white light source or laser is incident on the liquid surface obliquely, the phase distribution (cosine-like wave) generated by the light wave carrying the surface wave is first incident on the white paper which is located at the bottom of liquid, and the oscillator will also form the oscillator shadow on the white paper. The phase distribution of the light wave on the white paper spreads around dynamically in the form of cosine wave centering on the oscillator shadow. After diffuse reflection from the white paper, part of the diffuse reflection light in the observation direction carries the dynamic phase generated by the surface wave the first time back to the liquid surface and meets the surface wave again. After the light wave passes through the surface, it carries the phase generated by the surface wave the second time, that is, the superposition of two surface waves occurs in the phase of the light wave. In the phase of the light wave, the phase wave of the oscillator will propagate in the direction of the oscillator shadow, and the phase wave of the oscillator shadow will propagate in the direction of the oscillator. According to the conditions of forming standing waves, two surface waves propagating in the opposite directions can form standing waves, so the phase standing waves can exist only within a relatively small range between the oscillator and the oscillator shadow. Thus the dark and bright “self-interference” with stable stripes can be observed in the far field. When white light and laser are used as light sources respectively, the fringe spacing remains unchanged, indicating that the fringe spacing is independent of the wavelength of incident light, and the light wave is only the carrier of the mechanical wave phase. The light waves with different wavelengths and coherences have no influence on the experimental measurement results. The fringe spacing is measured automatically by analyzing and processing the image captured by camera. According to the dispersion relationship of surface waves, the surface tension coefficient of water is obtained automatically and accurately. The experimental setup is simple and easy to operate, the experimental phenomenon is intuitive, the stripes are clear and stable, and the anti-interference capability is strong, and can be observed in all directions. It can be widely used to measure the surface tension coefficients of other transparent liquids. -
Keywords:
- self-interference /
- standing wave phase /
- surface tension coefficient
[1] Javadi A, Habibi M, Taheri F S, Moulinet S, Bonn D 2013 Sci. Rep. 3 1412
Google Scholar
[2] Lee J H, Kim C J 2000 J. Microelectromech. Syst. 9 171
Google Scholar
[3] Ragesh P, Ganesh V A, Nair S V, Nair A S 2014 J. Mater. Chem. A 2 14773
Google Scholar
[4] López C, Hirsa A 2008 Nat. Photon. 2 610
Google Scholar
[5] Nazmul H, Hanseup K, and Carlos H M 2016 Opt. Express 24 13334
Google Scholar
[6] Na X 2021 Chin. Phys. B 30 104702
Google Scholar
[7] Michela P, Vladimir V R, Marcella I 2022 J. Phys. Condens. Matter 34 044003
Google Scholar
[8] Polovnikov K E, Gumerov R A, Potemkin I I 2016 Macromolecules 49 6599
Google Scholar
[9] Kou H B, Li W G, Zhang X Y, Xu N D, Zhang X H, Shao J X, Ma J Z, Deng Y, Li Y 2019 Fluid Phase Equilib. 484 53
Google Scholar
[10] Dogan A, Arslan H 2018 Philos. Mag. 98 2529
Google Scholar
[11] Mengsu P, Timothy T D, Cuong V N, Anh V N 2021 Langmuir 37 2237
Google Scholar
[12] 张福建, 陈悦, 高翔, 刘珍, 张忠强 2021 70 200202
Google Scholar
Zhang F J, Chen Y, Gao X, Liu Z, Zhang Z Q 2021 Acta Phys. Sin. 70 200202
Google Scholar
[13] Tang L, Liu G N, Qian J et al. 2016 Eur. J. Phys. 37 025801
Google Scholar
[14] Saepuzaman D, Nugraha M G, Dewi R et al. 2018 Pertanika J. Sci. Technol. 26 1435
[15] Samad A, Siamak M, Mohsen M, Mohammad T A, Farhad S 2008 J. Chem. Chem. Eng. 27 7
[16] Christov N C, Danov K D, Kralchevsky P A, et al. 2006 Langmuir 22 7528
Google Scholar
[17] Zhu F, Miao R C, Xu C L, Cao Z Z 2007 Am. J. Phys. 75 896
Google Scholar
[18] Luo D B, Qian L L, Dong L W, Shao P, Yue Z M, Wang J, Shi B, Wu S B, Qin Y P 2019 Opt. Express 27 16703
Google Scholar
[19] Nikolic D, Nesic L 2012 Eur. J. Phys. 33 1677
Google Scholar
[20] Lighthil J 1978 Waves in Fluids (Cambridge: Cambridge University Press)
[21] Behroozi F, Perkins A 2006 Am. J. Phys. 74 957
Google Scholar
[22] Crawford F S 1987 Am. J. Phys. 55 171
Google Scholar
-
图 1 测量装置示意图
Figure 1. Schematic diagram of measuring device.
图 2 光照射下水面波形成的明暗相间条纹
Figure 2. Light and dark streaks formed by water surface wave under light irradiation.
图 3 (a) “相位驻波”法测量液体的表面张力系数的实验原理示意图; (b) 实验原理的等效示意图
Figure 3. (a) Schematic diagram of measuring the surface tension coefficient of liquid by “phase standing wave” method; (b) an equivalent schematic of the experimental principle
图 4 相位波分布及摄像头处的光强数值模拟图
Figure 4. Phase wave distribution and numerical simulation of light intensity at the camera.
图 5 不同频率下的“自干涉”条纹
Figure 5. “Self-interference” fringes at different frequencies.
图 6 (a) 激光照射下液体表面波形成的条纹图像; (b) 激光和白光照射下液体表面波形成的条纹对比图
Figure 6. (a) Fringes formed by liquid surface wave under laser irradiation; (b) contrast of the fringes formed by liquid surface waves illuminated by laser and white light.
表 1 不同频率下自来水表面张力系数的测量结果
Table 1. Measurement results of surface tension coefficient of water at different frequencies.
序号 频率
f/Hz亮纹间距
d/mm表面张力系数
${ {\sigma } }_{ {i} }$/(10–3 N·m–1)1 60 2.479 69.8 2 80 2.052 70.4 3 100 1.756 68.9 4 120 1.574 71.5 5 140 1.404 69.1 6 160 1.296 71.0 7 180 1.188 69.2 
DownLoad: CSV
表 2 频率为100 Hz时, 自来水和含洗手液水溶液的表面张力系数测量结果
Table 2. Measurement results of surface tension coefficient of water and aqueous solution containing hand sanitizer at the frequency of 100 Hz.
序
号自来水 水溶液(含洗手液) 亮纹间距
d/mm表面张力系数
$\sigma_i$/(10–3 N·m–1)亮纹间距
d/mm表面张力系数
$\sigma_i$/(10–3 N·m–1)1 1.756 68.9 1.512 44.0 2 1.763 69.8 1.506 43.5 3 1.764 69.9 1.487 41.9 4 1.748 68.0 1.487 41.9 5 1.742 67.3 1.494 42.5 6 1.754 68.7 1.490 42.1
DownLoad: CSV
-
[1] Javadi A, Habibi M, Taheri F S, Moulinet S, Bonn D 2013 Sci. Rep. 3 1412
Google Scholar
[2] Lee J H, Kim C J 2000 J. Microelectromech. Syst. 9 171
Google Scholar
[3] Ragesh P, Ganesh V A, Nair S V, Nair A S 2014 J. Mater. Chem. A 2 14773
Google Scholar
[4] López C, Hirsa A 2008 Nat. Photon. 2 610
Google Scholar
[5] Nazmul H, Hanseup K, and Carlos H M 2016 Opt. Express 24 13334
Google Scholar
[6] Na X 2021 Chin. Phys. B 30 104702
Google Scholar
[7] Michela P, Vladimir V R, Marcella I 2022 J. Phys. Condens. Matter 34 044003
Google Scholar
[8] Polovnikov K E, Gumerov R A, Potemkin I I 2016 Macromolecules 49 6599
Google Scholar
[9] Kou H B, Li W G, Zhang X Y, Xu N D, Zhang X H, Shao J X, Ma J Z, Deng Y, Li Y 2019 Fluid Phase Equilib. 484 53
Google Scholar
[10] Dogan A, Arslan H 2018 Philos. Mag. 98 2529
Google Scholar
[11] Mengsu P, Timothy T D, Cuong V N, Anh V N 2021 Langmuir 37 2237
Google Scholar
[12] 张福建, 陈悦, 高翔, 刘珍, 张忠强 2021 70 200202
Google Scholar
Zhang F J, Chen Y, Gao X, Liu Z, Zhang Z Q 2021 Acta Phys. Sin. 70 200202
Google Scholar
[13] Tang L, Liu G N, Qian J et al. 2016 Eur. J. Phys. 37 025801
Google Scholar
[14] Saepuzaman D, Nugraha M G, Dewi R et al. 2018 Pertanika J. Sci. Technol. 26 1435
[15] Samad A, Siamak M, Mohsen M, Mohammad T A, Farhad S 2008 J. Chem. Chem. Eng. 27 7
[16] Christov N C, Danov K D, Kralchevsky P A, et al. 2006 Langmuir 22 7528
Google Scholar
[17] Zhu F, Miao R C, Xu C L, Cao Z Z 2007 Am. J. Phys. 75 896
Google Scholar
[18] Luo D B, Qian L L, Dong L W, Shao P, Yue Z M, Wang J, Shi B, Wu S B, Qin Y P 2019 Opt. Express 27 16703
Google Scholar
[19] Nikolic D, Nesic L 2012 Eur. J. Phys. 33 1677
Google Scholar
[20] Lighthil J 1978 Waves in Fluids (Cambridge: Cambridge University Press)
[21] Behroozi F, Perkins A 2006 Am. J. Phys. 74 957
Google Scholar
[22] Crawford F S 1987 Am. J. Phys. 55 171
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5075
- PDF Downloads: 93
- Cited By: 0
