-
The properties of ultrasonic nonlinear surface wave in the quasilinear region are investigated. In this work the governing equation of particle displacement potential is employed for surface wave in isotropic elastic solid with quadratic nonlinearity. Then, the quasilinear solution of the nonlinear surface wave is obtained by the perturbation method, and the absolute nonlinear parameter of the surface wave is derived. Subsequently, the main components of the second harmonic surface wave solution are discussed. A finite element model for the propagating nonlinear surface wave is developed, and simulation results of the nonlinear surface wave displacements agree well with the theoretical solutions, which indicates that the proposed theory is effective. Finally, the properties of wave propagation and the characteristic of the nonlinear parameter for the surface wave are analyzed based on the theoretical solutions. It is found that the second harmonic surface wave consists of cumulative and non-cumulative displacement terms. The cumulative displacement term is related to the self-interaction of the longitudinal wave component of the surface wave. However, its amplitude is larger than that of the pure longitudinal wave when the initial excitation conditions and propagation distances are the same. The nonlinear parameters for surface and longitudinal waves are related to each other, and an explicit relationship is found, which can be determined by the second-order elastic coefficients of the material. The propagation properties of nonlinear surface waves and the measurement method of absolute nonlinear parameters are also discussed, which will benefit the practical application of nonlinear surface waves.
-
Keywords:
- nonlinear surface wave /
- perturbation theory /
- nonlinear parameter /
- finite element modeling simulation
[1] 周正干, 刘斯明 2011 机械工程学报 47 2
Zhou Z G, Liu S M 2011 J. Mech. Eng. 47 2
[2] Huang Y, Wang X, Gong X, Wu H, Zhang D, Zhang D 2020 Sci. Rep. 10 1
[3] Matlack K H, Kim J Y, Jacobs L J, Qu J 2015 J. Nondestr. Eval. 34 273
Google Scholar
[4] 陈海霞, 林书玉 2021 70 114302
Google Scholar
Chen H X, Lin S Y 2021 Acta Phys. Sin. 70 114302
Google Scholar
[5] Zhang S, Li X, Chen C, Jeong H, Xu G 2019 J. Nondestr. Eval. 38 88
Google Scholar
[6] Liu Y, He A, Liu J, Mao Y, Liu X 2020 Chin. Phys. B 29 054301
Google Scholar
[7] Li W, Lan Z, Hu N, Deng M 2021 Ultrasonics 113 106356
Google Scholar
[8] Zhang J, Xuan F Z, Yang F 2013 J. NonCryst. Solids 378 101
Google Scholar
[9] Guo S, Lei Z, Mirshekarloo M S, Chen S, Yi F C, Zheng Z W, Shen Z, Liu H, Yao K 2016 Mater. Sci. Eng. A 669 41
Google Scholar
[10] Kim G, Park S, Kim J Y, Kurtis K E, Hayes N W, Jacobs L J 2018 Constr. Build. Mater. 186 1114
Google Scholar
[11] Torello D, Selby N, Kim J Y, Qu J, Jacobs L 2017 Ultrasonics 81 107
Google Scholar
[12] 张世功, 吴先梅, 张碧星, 安志武 2016 65 104301
Google Scholar
Zhang S G, Wu X M, Zhang B X, An Z W 2016 Acta Phys. Sin. 65 104301
Google Scholar
[13] Kube C M, Argulles A P 2017 J. Acoust. Soc. Am. 142 EL224
Google Scholar
[14] Wang X, Gong X, Qin C, Zhang D, Wu H, Zhang D 2019 Mech. Syst. Sig. Process. 130 790
Google Scholar
[15] Xu L, Wang K, Su Y, He Y, Yang J, Yuan S, Su Z 2021 Ultrasonics 118 106578
[16] Zabolotskaya E A 1992 J. Acoust. Soc. Am. 91 2569
Google Scholar
[17] Herrmann J, Kim J, Jacobs L J, Qu J, Littles J W, Savage M F 2006 J. Appl. Phys. 99 124913
Google Scholar
[18] Masurkar F, Tse P 2020 Ultrasonics 108 106036
Google Scholar
[19] Landau L D, Lifshitz E M 1986 Theory of Elasticity (Oxford: Pergamon Press) pp95–118
[20] Rose J L 2014 Ultrasonic Guided Waves in Solid Media (New York: Cambridge University Press) pp108–114
[21] Kundu T 2019 Nonlinear Ultrasonic and Vibro-acoustical Techniques for Nondestructive Evaluation (Gewerbestrasse: Springer Press) pp229–231
[22] Jia L, Yan S, Zhang B, Huang J 2020 J. Acoust. Soc. Am. 148 EL289
Google Scholar
[23] Norris A 1991 J. Elasticity 25 247
Google Scholar
[24] Nagy P B, Qu J, Jacobs L J 2013 J. Acoust. Soc. Am. 134 1760
Google Scholar
[25] Morlock M B, Kim J, Jacobs L J, Qu J 2015 J. Acoust. Soc. Am. 137 281
Google Scholar
[26] Muir D D. 2009 Ph. D. Dissertation (Atlanta: Georgia Institute of Technology)
[27] Zhong B, Zhu J 2021 Appl. Phys. Lett. 118 261903
Google Scholar
[28] Stobbe D M 2005 M. S. Thesis (Atlanta: Georgia Institute of Technology)
[29] de Araújo Freitas V L, de Albuquerque V H C, de Macedo Silva E, Silva A A, Tavares J M R 2010 Mater. Sci. Eng. A 527 4431
Google Scholar
[30] Shui Y, Solodov I Y 1988 J. Appl. Phys. 64 6155
Google Scholar
[31] Shull D J, Kim E E, Hamilton M F, Zabolotskaya E A 1995 J. Acoust. Soc. Am. 97 2126
Google Scholar
-
图 1 表面波传播坐标系
Figure 1. The coordinate for the propagation of the surface wave
图 2 非线性表面波二维有限元模型示意图
Figure 2. Schematic diagram of two-dimensional (2D) finite element model for nonlinear surface wave.
图 3 非线性纵波二维有限元模型示意图
Figure 3. Schematic diagram of 2D finite element model for the nonlinear longitudinal wave.
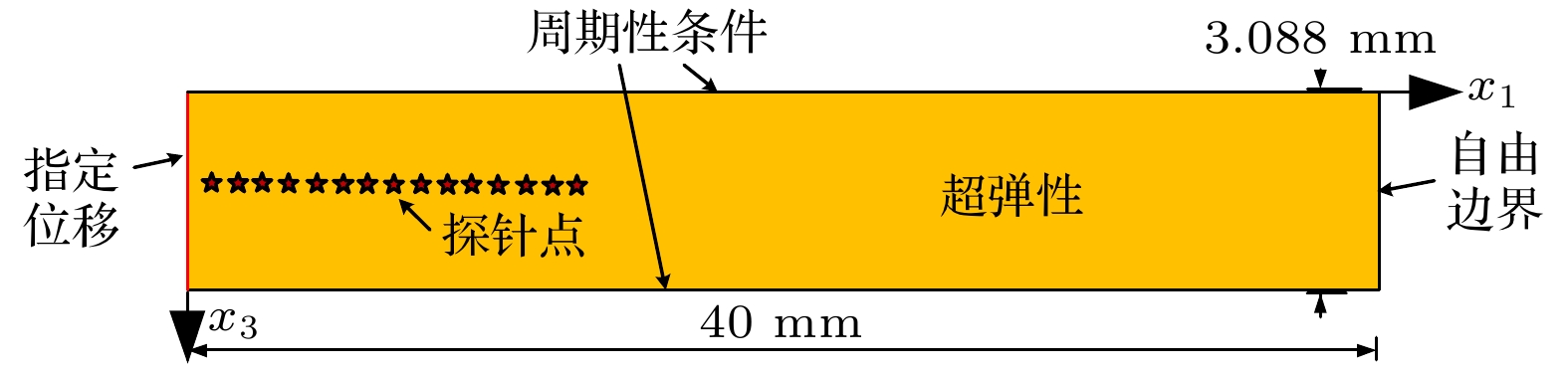
图 4 纵波仿真结果图 (a)传播距离15 mm处探针的信号图; (b) 基波和二次谐波幅值随距离变化图, 蓝色点是仿真结果, 黄色实线是线性拟合结果
Figure 4. Simulation results for the nonlinear longitudinal wave: (a) Typical signal at 15 mm propagation distance; (b) plots of fundamental wave and second harmonic amplitude versus propagation distance, where blue points denote the simulation results, and the yellow solid line denotes the fitting line.
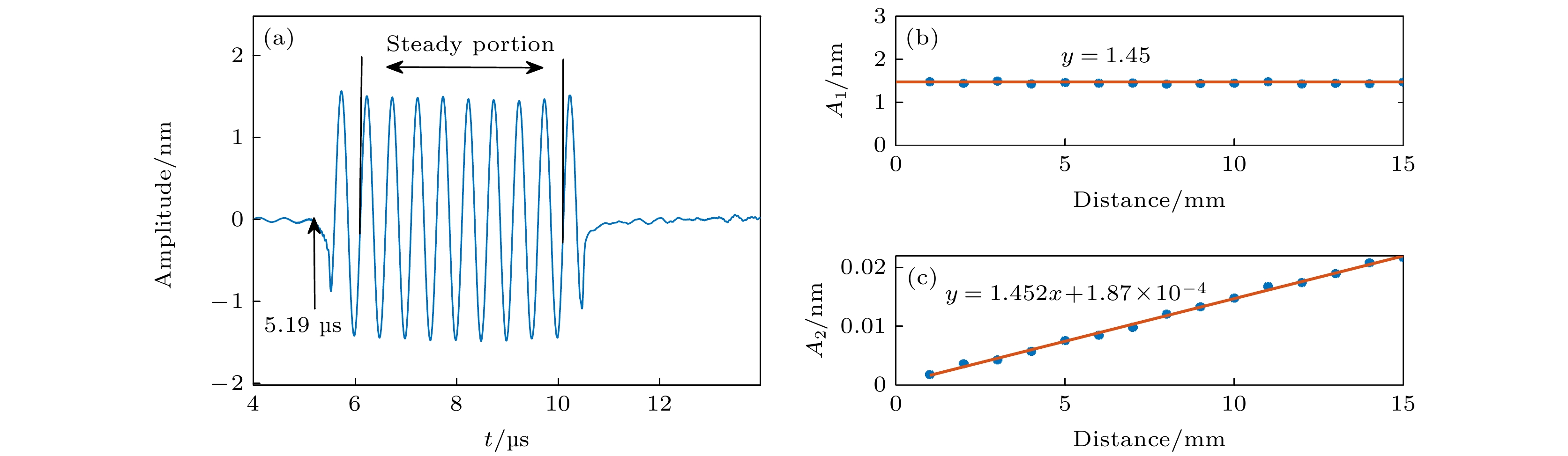
图 5 表面波仿真结果 (a) 传播距离15 mm处探针的信号图; (b) 基波和二次谐波幅值随距离变化图, 蓝色点是仿真结果, 黄色实线是拟合结果
Figure 5. Simulation results for the nonlinear surface wave: (a) Typical signal at 15 mm propagation distance; (b) plots of fundamental wave and second harmonic amplitude versus propagation distance, where blue points denote the simulation results, and the yellow solid line denotes the fitting line.
表 1 纯铝和三种铝合金的密度和弹性常数
Table 1. Densities and elastic coefficients of pure aluminum and three aluminum alloys.
DownLoad: CSV
表 2 初始条件和传播距离对面外分量和纵波二次谐波幅值的影响
Table 2. The effects of initial conditions and propagation distance on the amplitudes of out-of-plane component and the second harmonic longitudinal wave.
序号 传播距离r/m 频率f/MHz 基波幅值${A_1}$/nm 二次谐波幅值 ${A_2}$/nm $A_2^{\text{C}}$/nm $u_{\text{l}}^{\left( 2 \right)}$/nm 1 0.2 1 1 2.91×10–3 3.05×10–5 3.80×10–4 2 0.2 0.2 1 1.16×10–4 6.11×10–6 1.52×10–5 3 0.2 1 5 7.28×10–2 7.62×10–4 9.48×10–3 4 0.5 1 1 2.91×10–2 1.22×10–4 3.80×10–3
DownLoad: CSV
材料 ${\beta _{\text{l}}}$ ${\beta _{\text{r}}}$ ${\bar \beta _{\text{r}}}$ $ {\bar \beta _{11}} $ ${\delta _{\text{R}}}$ Al 14.670 24.672 4.740 1.166 22.191 Al2024 9.680 15.799 3.044 0.674 13.892 Al6061 9.695 14.753 2.860 0.733 14.444 Al7075 13.723 22.271 4.293 1.024 21.227
DownLoad: CSV
-
[1] 周正干, 刘斯明 2011 机械工程学报 47 2
Zhou Z G, Liu S M 2011 J. Mech. Eng. 47 2
[2] Huang Y, Wang X, Gong X, Wu H, Zhang D, Zhang D 2020 Sci. Rep. 10 1
[3] Matlack K H, Kim J Y, Jacobs L J, Qu J 2015 J. Nondestr. Eval. 34 273
Google Scholar
[4] 陈海霞, 林书玉 2021 70 114302
Google Scholar
Chen H X, Lin S Y 2021 Acta Phys. Sin. 70 114302
Google Scholar
[5] Zhang S, Li X, Chen C, Jeong H, Xu G 2019 J. Nondestr. Eval. 38 88
Google Scholar
[6] Liu Y, He A, Liu J, Mao Y, Liu X 2020 Chin. Phys. B 29 054301
Google Scholar
[7] Li W, Lan Z, Hu N, Deng M 2021 Ultrasonics 113 106356
Google Scholar
[8] Zhang J, Xuan F Z, Yang F 2013 J. NonCryst. Solids 378 101
Google Scholar
[9] Guo S, Lei Z, Mirshekarloo M S, Chen S, Yi F C, Zheng Z W, Shen Z, Liu H, Yao K 2016 Mater. Sci. Eng. A 669 41
Google Scholar
[10] Kim G, Park S, Kim J Y, Kurtis K E, Hayes N W, Jacobs L J 2018 Constr. Build. Mater. 186 1114
Google Scholar
[11] Torello D, Selby N, Kim J Y, Qu J, Jacobs L 2017 Ultrasonics 81 107
Google Scholar
[12] 张世功, 吴先梅, 张碧星, 安志武 2016 65 104301
Google Scholar
Zhang S G, Wu X M, Zhang B X, An Z W 2016 Acta Phys. Sin. 65 104301
Google Scholar
[13] Kube C M, Argulles A P 2017 J. Acoust. Soc. Am. 142 EL224
Google Scholar
[14] Wang X, Gong X, Qin C, Zhang D, Wu H, Zhang D 2019 Mech. Syst. Sig. Process. 130 790
Google Scholar
[15] Xu L, Wang K, Su Y, He Y, Yang J, Yuan S, Su Z 2021 Ultrasonics 118 106578
[16] Zabolotskaya E A 1992 J. Acoust. Soc. Am. 91 2569
Google Scholar
[17] Herrmann J, Kim J, Jacobs L J, Qu J, Littles J W, Savage M F 2006 J. Appl. Phys. 99 124913
Google Scholar
[18] Masurkar F, Tse P 2020 Ultrasonics 108 106036
Google Scholar
[19] Landau L D, Lifshitz E M 1986 Theory of Elasticity (Oxford: Pergamon Press) pp95–118
[20] Rose J L 2014 Ultrasonic Guided Waves in Solid Media (New York: Cambridge University Press) pp108–114
[21] Kundu T 2019 Nonlinear Ultrasonic and Vibro-acoustical Techniques for Nondestructive Evaluation (Gewerbestrasse: Springer Press) pp229–231
[22] Jia L, Yan S, Zhang B, Huang J 2020 J. Acoust. Soc. Am. 148 EL289
Google Scholar
[23] Norris A 1991 J. Elasticity 25 247
Google Scholar
[24] Nagy P B, Qu J, Jacobs L J 2013 J. Acoust. Soc. Am. 134 1760
Google Scholar
[25] Morlock M B, Kim J, Jacobs L J, Qu J 2015 J. Acoust. Soc. Am. 137 281
Google Scholar
[26] Muir D D. 2009 Ph. D. Dissertation (Atlanta: Georgia Institute of Technology)
[27] Zhong B, Zhu J 2021 Appl. Phys. Lett. 118 261903
Google Scholar
[28] Stobbe D M 2005 M. S. Thesis (Atlanta: Georgia Institute of Technology)
[29] de Araújo Freitas V L, de Albuquerque V H C, de Macedo Silva E, Silva A A, Tavares J M R 2010 Mater. Sci. Eng. A 527 4431
Google Scholar
[30] Shui Y, Solodov I Y 1988 J. Appl. Phys. 64 6155
Google Scholar
[31] Shull D J, Kim E E, Hamilton M F, Zabolotskaya E A 1995 J. Acoust. Soc. Am. 97 2126
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4712
- PDF Downloads: 82
- Cited By: 0
