-
The prediction of nonlinear and non-stationary systems is a research topic of great scientific significance. In some recent work the convergent cross mapping (CCM) algorithm is used to detect the causal relationship between variables. In the CCM algorithm, the points close to each other in the phase space have similar trends and trajectories in time. Therefore, this method can be applied to the prediction of experimental researches of nonlinear and non-stationary systems. Therefore, in this paper the CCM algorithm is applied to the prediction of the Lorenz system and the actual climate time series, and the effects of different phase space reconstruction methods on the prediction skill are investigated. The preliminary results are as follows. 1) No matter whether the ideal Lorenz model or the actual climate series, of the three reconstruction phase space methods of univariate, multivariate, and multiview embedding method, the multiview embedding method is the best predictive skill, indicating that for a given length of time series, the more the information contained in the reconstructed phase space, the stronger its predictive ability is. 2) Adding the data of NAM (northern hemisphere annular mode) to the reconstructed phase space of SAT (surface air temperature) can improve the prediction effect on prediction of SAT. Using the univariable, multivariable, and multiview embedding method for implementing prediction, the characteristics of common information in the complex system are considered. On condition that the length of the time series is fixed, the complexity of the dynamic system can be used to increase the information of the system. Based on causality detection, through the extraction of quantitative information of data, a novel idea for the improvement of predictive skills in nonlinear and non-stationary systems can be obtained.
-
Keywords:
- convergent cross mapping /
- causality /
- nonlinear prediction /
- nonlinear system
[1] 魏凤英 2006 应用气象学报 6 736
Google Scholar
Wei F Y 2006 J. Appl. Meteor. Sci. 6 736
Google Scholar
[2] 丁瑞强, 李建平 2009 气象学报 67 241
Google Scholar
Ding R Q, Li J P 2009 Acta Meteor Sin. 67 241
Google Scholar
[3] Li H R, Jin F F, Song L C 2017 J. Meteorol. Res. 31 204
Google Scholar
[4] 丁一汇 2004 气象 30 11
Google Scholar
Ding Y H 2004 Meteor. Mon. 30 11
Google Scholar
[5] 徐邦琪, 臧钰歆, 朱志伟 2020 大气科学学报 43 212
Hsu P C, Zang Y X, Zhu Z W 2020 Trans. Atmos. Sci. 43 212
[6] 杨培才, 卞建春, 王革丽, 周秀骥 2003 科学通报 48 1470
Google Scholar
Yang P C, Bian J C, Wang G L, Zhou X J 2003 Chin. Sci. Bull. 48 1470
Google Scholar
[7] Packard N H, Crutchfield J P, Farmer J D, Shaw R S 1980 Phys. Rev. Lett. 45 712
Google Scholar
[8] Takens F 1981 Lect. Notes Math. 898 366
[9] Farmer J D, Sidorowich J 1987 Phys. Rev. Lett. 59 845
Google Scholar
[10] Casdagli M 1989 Phys. D 35 335
Google Scholar
[11] Yang P C, Zhou X J, Bian J C 2000 J. Geophys. Res. 105 12253
Google Scholar
[12] Wang G L, Yang P C, Lv D R 2004 Adv. Atmos. Sci. 21 296
Google Scholar
[13] 潘昕浓, 王革丽, 杨培才 2017 66 080501
Google Scholar
Pan X N, Wang G L, Yang P C 2017 Acta Phys. Sin. 66 080501
Google Scholar
[14] 陈潇潇, 王革丽, 金莲姬 2015 中国环境科学 35 694
Chen X X, Wang G L, Jin L J 2015 China Environ. Sci. 35 694
[15] 杨培才, 周秀骥 2005 气象学报 63 556
Google Scholar
Yang P C, Zhou X J 2005 Acta Meteor. Sin. 63 556
Google Scholar
[16] Verdes P F, Granitto P M, Navone H D, Ceccatto H A 2001 Phys. Rev. Lett. 87 124101
Google Scholar
[17] Wiskott L 2003 Neural Comput. 15 2147
Google Scholar
[18] Verdes P F 2007 Phys. Rev. Lett. 99 1
[19] Gunturkun U 2010 Phys. D. 239 1095
Google Scholar
[20] Wiener N (Beckenbach E F Ed.) 1956 Modern Mathermatics for Engineers p165
[21] Granger C W J 1969 Econometrica 37 424
Google Scholar
[22] Barnett L, Barrett A B, Seth A K 2009 Phys. Rev. Lett. 103 238701
Google Scholar
[23] Bressler, Steven L, Seth A K 2011 NeuroImage 58 323
Google Scholar
[24] Sugihara G, May R M, Ye H 2012 Science 338 496
Google Scholar
[25] Deyle E R, Maher M C, Hernandez R D 2016 PNAS 113 13081
Google Scholar
[26] Runge J, Bathiany S, Bollt E 2019 Nat. Commun. 10 2553
Google Scholar
[27] Tsonis A A, Deyle E R, May R M 2015 PNAS 112 3253
Google Scholar
[28] Zhang N N, Wang G L, Tsonis A A 2019 Climate DyNAMics 52 3175
Google Scholar
[29] Sugihara G, May R M 1990 Nature 344 734
Google Scholar
[30] Dixon P A, Milicich M J, Sugihara G 2001 Nonlinear Dynamics and Statistics (Boston: Birkhauser) p339
[31] Sugihara G 1994 Philos. Trans. Royal Soc. 348 477
[32] Dixon P A, Milicich M J, Sugihara G 1999 Science 283 1528
Google Scholar
[33] Ye H, Sugihara G 2016 Science 335 922
[34] Lorenz E N 1963 J. Atmos. Sci. 20 130
Google Scholar
-
图 1 最佳嵌入维数E的选取
Figure 1. Selection of the best embedding dimension E.
图 2 (a)单变量嵌入法预测结果; (b)多变量嵌入法预测结果; (c)多视角嵌入法预测结果; (d)三种嵌入法预测结果的平均绝对误差比较
Figure 2. Forecast results: (a) Univariate embedding; (b) multivariate embedding; (c) multiview embedding; (d) average absolute error of the prediction results of the three embedding methods.
图 3 三种嵌入方法预测能力随步长的变化 (a)单变量嵌入法; (b)多变量嵌入法; (c)多视角嵌入法
Figure 3. The prediction ability of three embedding methods varies with step size: (a)Univariate embedding; (b) multivariate embedding; (c) multiview embedding;.
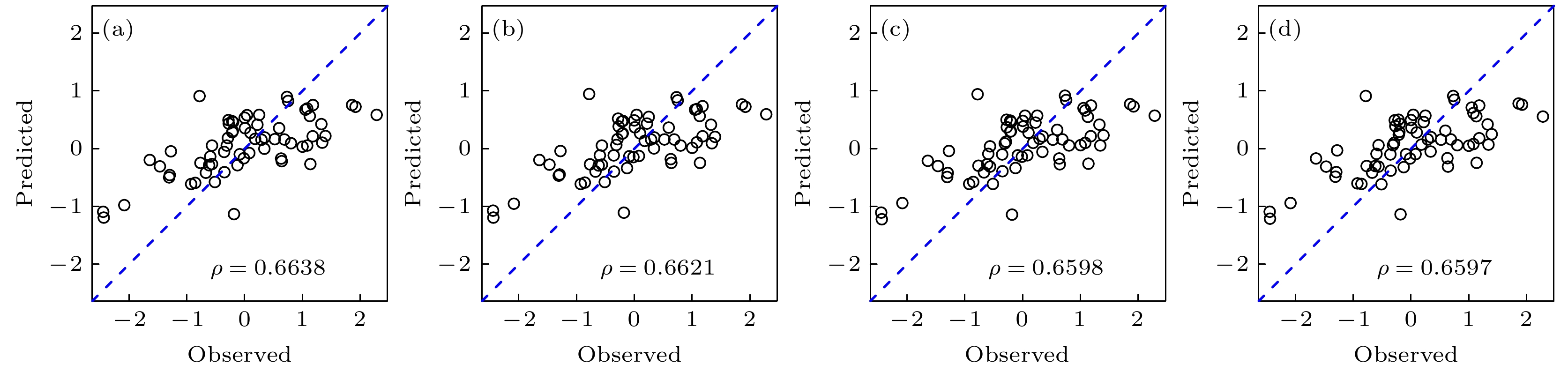
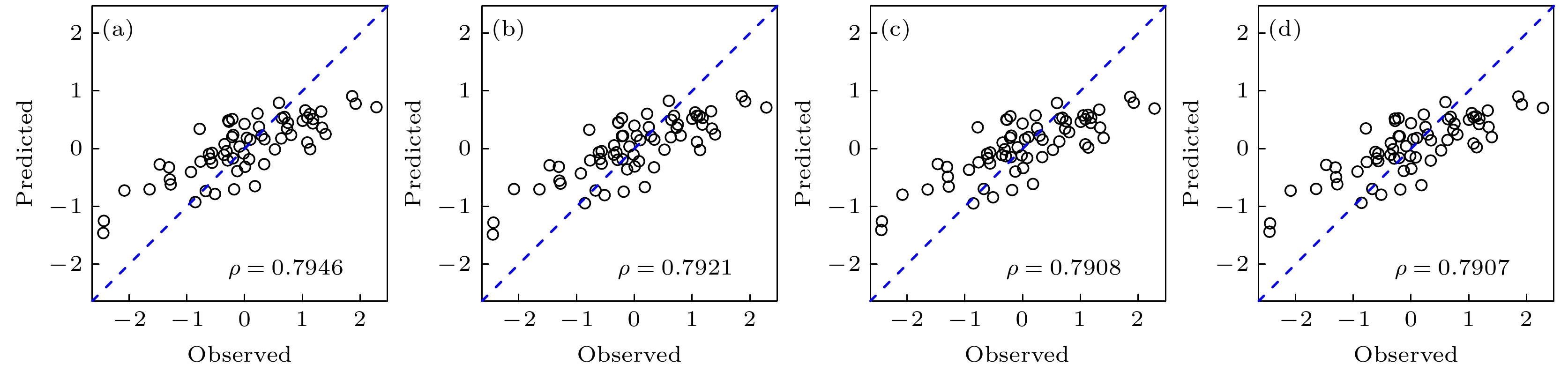
图 4 (a)单变量嵌入法和在目标变量中加入NAM信号后的预测结果; (b)多变量嵌入法的预测结果(黑色圆圈代表仅利用SAT序列进行预测, 红色三角代表加入NAM信号后)
Figure 4. (a) Univariate embedding method and prediction result after adding NAM signal to the target variable; (b) prediction result of multivariate embedding method (black circle represents prediction using only SAT sequence, red triangle represents after adding NAM signal).
图 5 仅用东北亚地区冬季SAT重构相空间, (a)—(d)分别表示k取40, 41, 42, 43的预测结果
Figure 5. Only using Northeast Asia winter surface air temperature reconstruct the phase space: (a)–(d) represent the prediction results of k taking 40, 41, 42, 43 respectively.
图 6 仅将2月的NAM信号加入SAT的重构相空间中, (a)—(d)分别表示k取30, 36, 31, 34的预测结果
Figure 6. Only adding the NAM signal in February to the reconstructed phase space of the SAT: (a)–(d) represent the prediction results of k taking 30, 36, 31, and 34, respectively.
图 7 将12月至次年2月的NAM信号加入SAT的重构相空间中, (a)—(d)分别表示当k取38, 39, 36, 37时的预测结果
Figure 7. Adding the NAM signals from December to next February to the reconstructed phase space of the SAT: (a)–(d) show the prediction results when k takes 38, 39, 36, and 37, respectively.
表 1 多种嵌入方法的预测结果
Table 1. Predicted results of multiple embedding methods.
Embedding method Reconstructing phase space with SAT only Adding NAM to SAT to reconstruct the phase space ρ MAE RMSE ρ MAE RMSE Univariate 0.12 1.06 1.30 0.18 0.97 1.18 Multivariate 0.15 1.02 1.27 0.26 0.95 1.12 Multi-angle 0.66 0.62 0.75 0.79 0.59 0.66 
DownLoad: CSV
-
[1] 魏凤英 2006 应用气象学报 6 736
Google Scholar
Wei F Y 2006 J. Appl. Meteor. Sci. 6 736
Google Scholar
[2] 丁瑞强, 李建平 2009 气象学报 67 241
Google Scholar
Ding R Q, Li J P 2009 Acta Meteor Sin. 67 241
Google Scholar
[3] Li H R, Jin F F, Song L C 2017 J. Meteorol. Res. 31 204
Google Scholar
[4] 丁一汇 2004 气象 30 11
Google Scholar
Ding Y H 2004 Meteor. Mon. 30 11
Google Scholar
[5] 徐邦琪, 臧钰歆, 朱志伟 2020 大气科学学报 43 212
Hsu P C, Zang Y X, Zhu Z W 2020 Trans. Atmos. Sci. 43 212
[6] 杨培才, 卞建春, 王革丽, 周秀骥 2003 科学通报 48 1470
Google Scholar
Yang P C, Bian J C, Wang G L, Zhou X J 2003 Chin. Sci. Bull. 48 1470
Google Scholar
[7] Packard N H, Crutchfield J P, Farmer J D, Shaw R S 1980 Phys. Rev. Lett. 45 712
Google Scholar
[8] Takens F 1981 Lect. Notes Math. 898 366
[9] Farmer J D, Sidorowich J 1987 Phys. Rev. Lett. 59 845
Google Scholar
[10] Casdagli M 1989 Phys. D 35 335
Google Scholar
[11] Yang P C, Zhou X J, Bian J C 2000 J. Geophys. Res. 105 12253
Google Scholar
[12] Wang G L, Yang P C, Lv D R 2004 Adv. Atmos. Sci. 21 296
Google Scholar
[13] 潘昕浓, 王革丽, 杨培才 2017 66 080501
Google Scholar
Pan X N, Wang G L, Yang P C 2017 Acta Phys. Sin. 66 080501
Google Scholar
[14] 陈潇潇, 王革丽, 金莲姬 2015 中国环境科学 35 694
Chen X X, Wang G L, Jin L J 2015 China Environ. Sci. 35 694
[15] 杨培才, 周秀骥 2005 气象学报 63 556
Google Scholar
Yang P C, Zhou X J 2005 Acta Meteor. Sin. 63 556
Google Scholar
[16] Verdes P F, Granitto P M, Navone H D, Ceccatto H A 2001 Phys. Rev. Lett. 87 124101
Google Scholar
[17] Wiskott L 2003 Neural Comput. 15 2147
Google Scholar
[18] Verdes P F 2007 Phys. Rev. Lett. 99 1
[19] Gunturkun U 2010 Phys. D. 239 1095
Google Scholar
[20] Wiener N (Beckenbach E F Ed.) 1956 Modern Mathermatics for Engineers p165
[21] Granger C W J 1969 Econometrica 37 424
Google Scholar
[22] Barnett L, Barrett A B, Seth A K 2009 Phys. Rev. Lett. 103 238701
Google Scholar
[23] Bressler, Steven L, Seth A K 2011 NeuroImage 58 323
Google Scholar
[24] Sugihara G, May R M, Ye H 2012 Science 338 496
Google Scholar
[25] Deyle E R, Maher M C, Hernandez R D 2016 PNAS 113 13081
Google Scholar
[26] Runge J, Bathiany S, Bollt E 2019 Nat. Commun. 10 2553
Google Scholar
[27] Tsonis A A, Deyle E R, May R M 2015 PNAS 112 3253
Google Scholar
[28] Zhang N N, Wang G L, Tsonis A A 2019 Climate DyNAMics 52 3175
Google Scholar
[29] Sugihara G, May R M 1990 Nature 344 734
Google Scholar
[30] Dixon P A, Milicich M J, Sugihara G 2001 Nonlinear Dynamics and Statistics (Boston: Birkhauser) p339
[31] Sugihara G 1994 Philos. Trans. Royal Soc. 348 477
[32] Dixon P A, Milicich M J, Sugihara G 1999 Science 283 1528
Google Scholar
[33] Ye H, Sugihara G 2016 Science 335 922
[34] Lorenz E N 1963 J. Atmos. Sci. 20 130
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4579
- PDF Downloads: 97
- Cited By: 0
