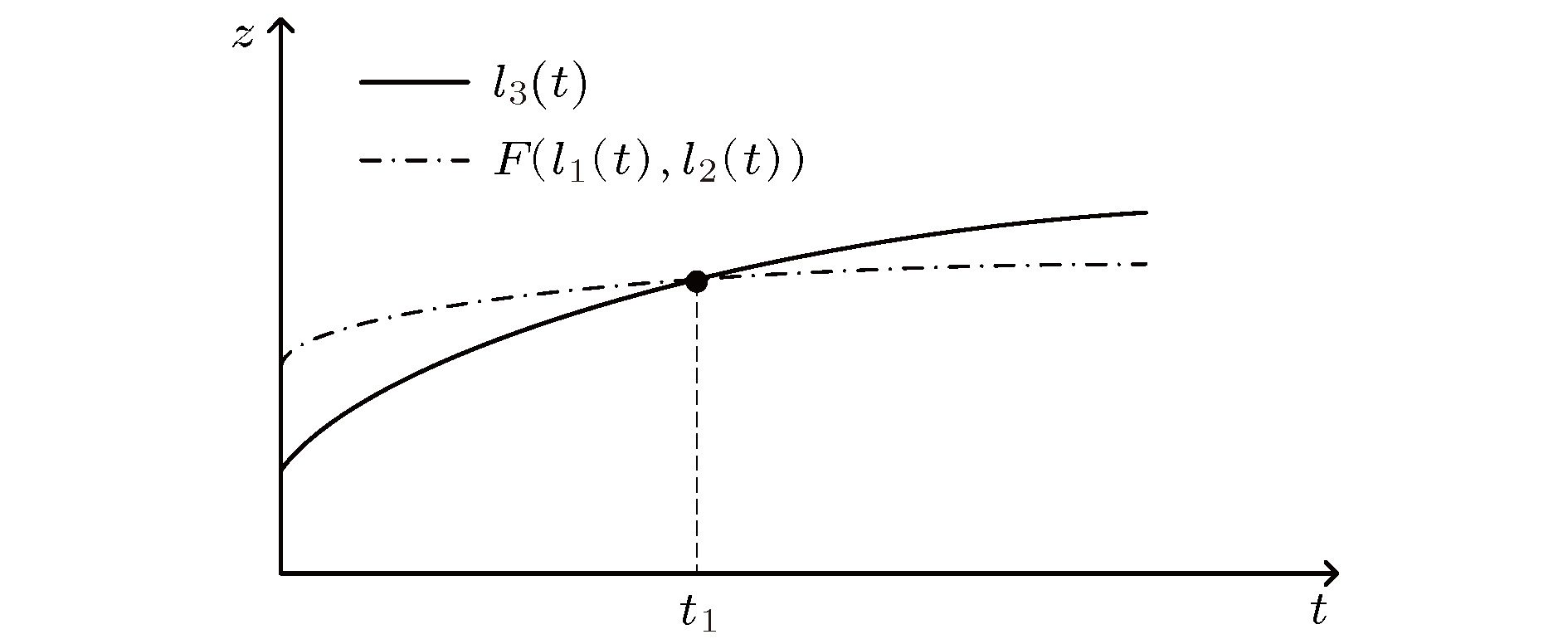
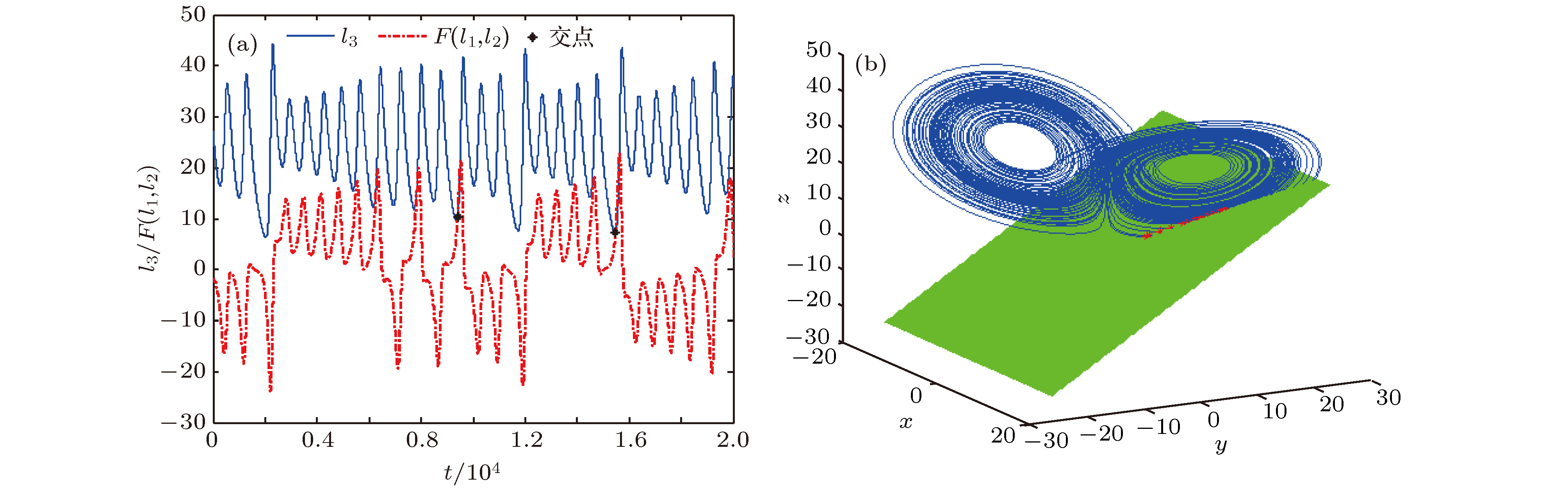
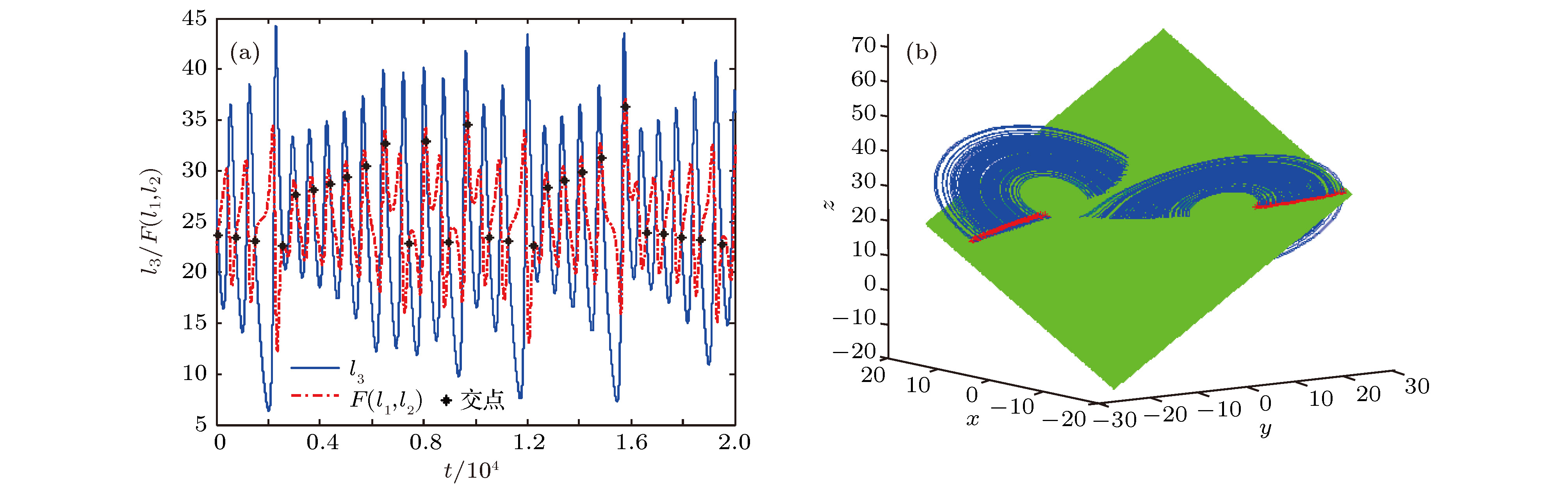
-
Poincare section is an important method for analyzing nonlinear systems. Choosing a suitable plane as the Poincare section is the key to using the Poincare section to analyze a nonlinear system. At present, it is still a difficult problem to select a suitable Poincare section when analyzing a nonlinear system. This is caused by two reasons. On the one hand, the classical method for selecting a partial Poincare section only applies to analyze a part of the nonlinear system orbit, whether the selected plane is a suitable Poincare section is affected by the different initial points. On the other hand, according to the actual situation, different researchers have different needs for Poincare section. In order to solve this problem, a new method named Projection Time Domain method is put forward in this paper. This method can help us not only directly reflect the intersection between the nonlinear system orbit and the selected plane, but also accurately adjust the direction and position of the selected plane in real time. It can be used to quickly find a plane which fully intersects the nonlinear system orbit or an arbitrary plane as a Poincare section. In this paper, the complete definition of Projection Time Domain method is given firstly. Then, the principle of Projection Time Domain method is theoretically analyzed in detail. At the same time, the rules for determining whether the selected plane is a suitable Poincare section in the time domain are also studied. Finally, it is introduced how to quantify the direction and position of the selected plane in the phase space. The simulation experiments are conducted with three typical three-dimensional and four-dimensional nonlinear systems by using this new method. The experimental results consistent with the theoretical analysis, which demonstrate the effectiveness and practicability of this method.
-
Keywords:
- Poincare section /
- time domain /
- nonlinear system
[1] 刘妮, 梁九卿 2017 66 110502
Liu N, Liang J Q 2017 Acta Phys. Sin. 66 110502
[2] Bastarrachea-Magnani M A, Lopez-del-Carpio B, Lerma-Hernandez S, Hirsch J G 2015 Phys. Scr 90 068015
[3] Kubin G N 1997 IEEE Workshop on Speech Coding for Telecommunications Proceedings. Back to Basics: Attacking Fundamental Problems in Speech Coding Pocono Manor, USA, Sept 7 - 10, 1997 p7
[4] Jafari A, Almasganj F, Bidhendi M N 2010 Chaos 20 033106
Google Scholar
[5] 霍铖宇, 庄建军, 黄晓林, 侯凤贞, 宁新宝 2012 61 190506
Huo C Y, Zhuang J J, Huang X L, Hou F Z, Ning X B 2012 Acta Phys. Sin. 61 190506
[6] 李洪云, 岳大光, 梁志强, 伊长虹, 陈建中 2018 62 203401
Google Scholar
Li H Y, Yue D G, Liang Z Q, Yi C H, Chen J Z 2018 Acta Phys. Sin. 62 203401
Google Scholar
[7] Tucker W 2002 Phys. D 171 127
Google Scholar
[8] 张波, 李忠, 毛宗源, 庞敏熙 2001 控制理论与应用 18 796
Google Scholar
Zhang B, Li Z, Mao Z Y, Pang M X 2001 Control Theory & Appl. 18 796
Google Scholar
[9] Golestani A, Jahed M M R, Ahmadian K, Omidvarnia A H, Mozayani N 2009 Chaos 19 013137
Google Scholar
[10] Wu W J, Chen Z Q, Yuan Z Z 2009 Chaos, Soliton. Fract. 41 2756
Google Scholar
[11] Stankevich N V, Kuznetsov A P, Popova E S, Seleznev E P 2017 Commun. Nonlinear Sci. 43 200
Google Scholar
[12] 王琳, 彭建华, 张立静 2007 深圳大学学报(理工版) 24 290
Wang L, Peng J H, Zhang L J 2007 J. Shenzhen U. Sci. Eng. 24 290
[13] 陈红, 吴玲 2013 62 020507
Chen H, Wu L 2013 Acta Phys. Sin. 62 020507
[14] Clare M J, Pieter J C, Bernd K, Hinke M O 2008 SIAM J. Appl. Dyn. Syst. 7 712
[15] 李正友, 李天伟, 黄谦, 郭姣 2012 应用声学 5 379
Google Scholar
Li Z Y, Li T W, Huang Q, Guo J 2012 Appl. Acoust. 5 379
Google Scholar
[16] Mukherjee S, Palit S K, Banerjee S, Wahab A W A, Ariffin M, Bhattacharya D K 2017 Appl. Math. Comput. 301 140
[17] Michalak K 2015 Chaos, Soliton. Fract. 78 215
Google Scholar
[18] Babak S, Amir H J 2015 Proceeding of the IEEE 28 th Canadian Conference on Electrical and Computer Engineering Halifax, Canada, May 3−6, 2015 p581
[19] Atefeh G, Ateke G 2018 Chaos, Soliton. Fract. 114 400
Google Scholar
[20] Carlos E C S, Daniel P B C 2019 IEEE Access 7 10523
Google Scholar
[21] 闫登卫, 王丽丹, 段书凯 2018 67 110502
Google Scholar
Yan D W, Wang L D, Duan S K 2018 Acta Phys. Sin. 67 110502
Google Scholar
[22] 禹思敏 2011 混沌系统与混沌电路(西安: 西安电子科技大学出版社) 第156页
Yu S M 2011 Chaotic systems and chaotic circuits (Xi’an: Xi’an Electronic University Press) p156 (in Chinese)
[23] 刘兴云, 鲁池梅, 程永山 2008 计算机测量与控制 16 834
Liu X Y, Lü C M, Cheng Y S 2008 Computer Measurement & Contrl 16 834
[24] 蔡娜, 井元伟, 姜囡, 张嗣瀛 2009 东北大学学报(自然科学版) 30 313
Cai N, Jing Y W, Jiang C, Zhang S Y 2009 J. Northeast Univ. 30 313
-
图 2
$F({l_1}(t), {l_2}(t))$ 与${l_3}(t)$ 的波形Fig. 2. Waveform of
$F({l_1}(t), {l_2}(t))$ and${l_3}(t)$ .
图 3 涡卷的相轨与波形 (a)相轨; (b)波形
Fig. 3. Phase trajectoy and waveform of vortex: (a) Phase trajectoy; (b) waveform.
图 4 平面一的实验结果 (a)时域波形; (b)相图
Fig. 4. Experimental results of the first plane: (a) Waveform; (b) phase diagram.
图 5 平面二的实验结果 (a)时域波形; (b)相图
Fig. 5. Experimental results of the second plane: (a) Waveform;(b) phase diagram.
图 6 平面三的实验结果 (a)时域波形; (b)相图
Fig. 6. Experimental results of the third plane: (a) Waveform; (b) phase diagram.
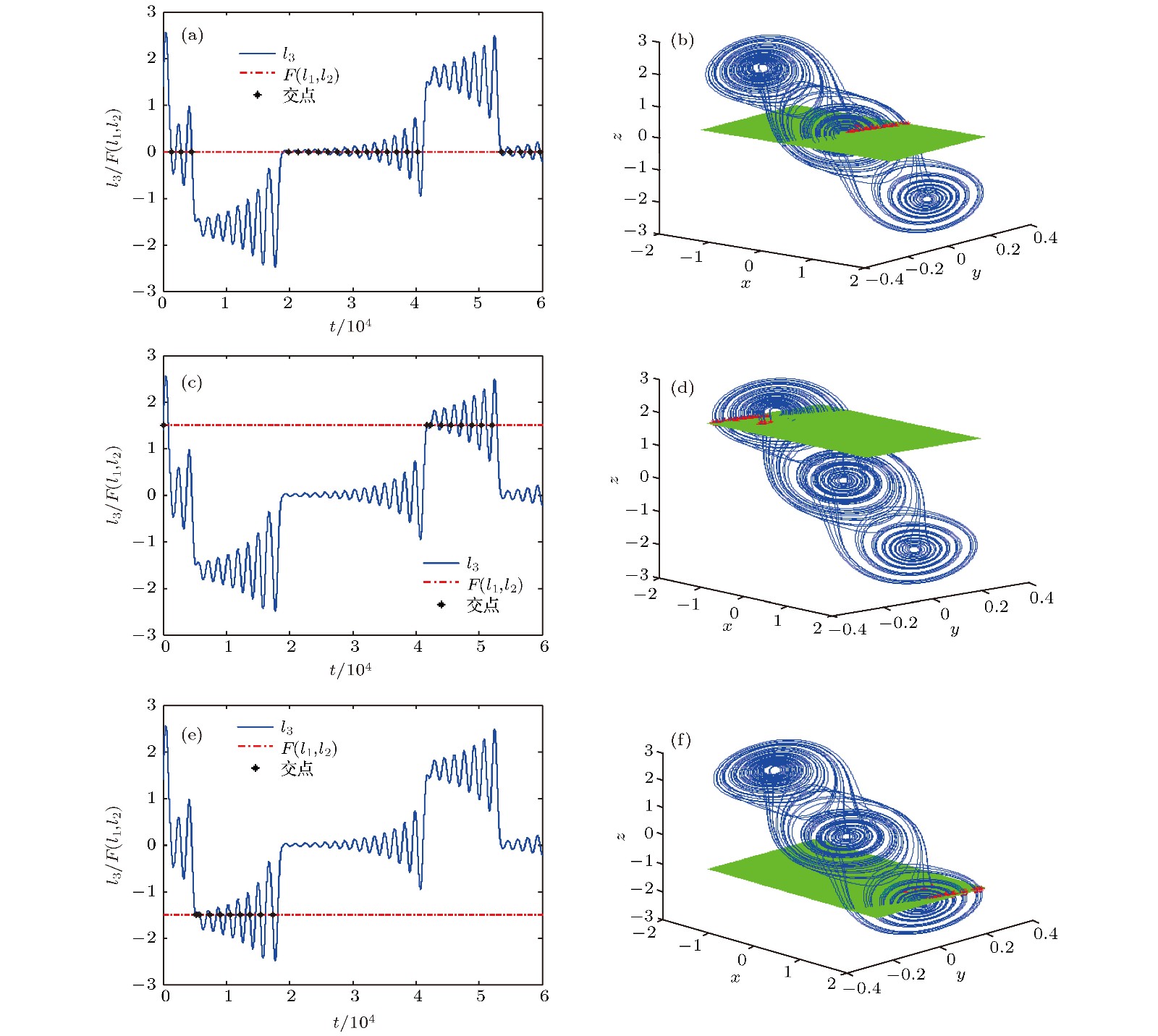
图 7 平面一的实验结果 (a) C = 0时的波形; (b) C = 0时的相图; (c) C = 1.5时的波形; (d) C = 1.5时的相图; (e) C = –1.5时的波形; (f) C = –1.5时的相图
Fig. 7. Experimental results of the first plane: (a) Waveform while C = 0; (b) phase diagram while C = 0; (c) waveform while C = 1.5; (d) phase diagram while C = 1.5; (e) waveform while C = –1.5; (f) phase diagram while C = –1.5.
图 8 平面二的实验结果 (a)波形; (b)相图
Fig. 8. Experimental results of the second plane: (a) Waveform; (b) phase diagram.
图 9
$w = 0$ 时的实验结果 (a)波形; (b)相图Fig. 9. Experimental results while
$w = 0$ : (a) Waveform; (b) phase diagram.
图 10
$z = 0$ 时的实验结果 (a)波形; (b)相图Fig. 10. Experimental results while
$z = 0$ : (a) Waveform; (b) phase diagram.
图 11
$y = 0$ 时的实验结果 (a)波形; (b)相图Fig. 11. Experimental results while
$y = 0$ : (a) Waveform; (b) phase diagram.
图 12
$x = 0$ 时的实验结果 (a)波形; (b)相图Fig. 12. Experimental results while
$x = 0$ : (a) Waveform; (b) phase diagram.表 1 常用平面的参数值
Table 1. Parameter values of typical planes.
序号 ${\theta _1}$/(º) ${\theta _2}$/(º) A B 1 0 0 0 0 2 0 45 0 1 3 0 60 0 $\sqrt 3 $ 4 0 135 0 –1 5 45 0 1 0 6 60 0 $\sqrt 3 $ 0 7 135 0 –1 0 
下载: 导出CSV
-
[1] 刘妮, 梁九卿 2017 66 110502
Liu N, Liang J Q 2017 Acta Phys. Sin. 66 110502
[2] Bastarrachea-Magnani M A, Lopez-del-Carpio B, Lerma-Hernandez S, Hirsch J G 2015 Phys. Scr 90 068015
[3] Kubin G N 1997 IEEE Workshop on Speech Coding for Telecommunications Proceedings. Back to Basics: Attacking Fundamental Problems in Speech Coding Pocono Manor, USA, Sept 7 - 10, 1997 p7
[4] Jafari A, Almasganj F, Bidhendi M N 2010 Chaos 20 033106
Google Scholar
[5] 霍铖宇, 庄建军, 黄晓林, 侯凤贞, 宁新宝 2012 61 190506
Huo C Y, Zhuang J J, Huang X L, Hou F Z, Ning X B 2012 Acta Phys. Sin. 61 190506
[6] 李洪云, 岳大光, 梁志强, 伊长虹, 陈建中 2018 62 203401
Google Scholar
Li H Y, Yue D G, Liang Z Q, Yi C H, Chen J Z 2018 Acta Phys. Sin. 62 203401
Google Scholar
[7] Tucker W 2002 Phys. D 171 127
Google Scholar
[8] 张波, 李忠, 毛宗源, 庞敏熙 2001 控制理论与应用 18 796
Google Scholar
Zhang B, Li Z, Mao Z Y, Pang M X 2001 Control Theory & Appl. 18 796
Google Scholar
[9] Golestani A, Jahed M M R, Ahmadian K, Omidvarnia A H, Mozayani N 2009 Chaos 19 013137
Google Scholar
[10] Wu W J, Chen Z Q, Yuan Z Z 2009 Chaos, Soliton. Fract. 41 2756
Google Scholar
[11] Stankevich N V, Kuznetsov A P, Popova E S, Seleznev E P 2017 Commun. Nonlinear Sci. 43 200
Google Scholar
[12] 王琳, 彭建华, 张立静 2007 深圳大学学报(理工版) 24 290
Wang L, Peng J H, Zhang L J 2007 J. Shenzhen U. Sci. Eng. 24 290
[13] 陈红, 吴玲 2013 62 020507
Chen H, Wu L 2013 Acta Phys. Sin. 62 020507
[14] Clare M J, Pieter J C, Bernd K, Hinke M O 2008 SIAM J. Appl. Dyn. Syst. 7 712
[15] 李正友, 李天伟, 黄谦, 郭姣 2012 应用声学 5 379
Google Scholar
Li Z Y, Li T W, Huang Q, Guo J 2012 Appl. Acoust. 5 379
Google Scholar
[16] Mukherjee S, Palit S K, Banerjee S, Wahab A W A, Ariffin M, Bhattacharya D K 2017 Appl. Math. Comput. 301 140
[17] Michalak K 2015 Chaos, Soliton. Fract. 78 215
Google Scholar
[18] Babak S, Amir H J 2015 Proceeding of the IEEE 28 th Canadian Conference on Electrical and Computer Engineering Halifax, Canada, May 3−6, 2015 p581
[19] Atefeh G, Ateke G 2018 Chaos, Soliton. Fract. 114 400
Google Scholar
[20] Carlos E C S, Daniel P B C 2019 IEEE Access 7 10523
Google Scholar
[21] 闫登卫, 王丽丹, 段书凯 2018 67 110502
Google Scholar
Yan D W, Wang L D, Duan S K 2018 Acta Phys. Sin. 67 110502
Google Scholar
[22] 禹思敏 2011 混沌系统与混沌电路(西安: 西安电子科技大学出版社) 第156页
Yu S M 2011 Chaotic systems and chaotic circuits (Xi’an: Xi’an Electronic University Press) p156 (in Chinese)
[23] 刘兴云, 鲁池梅, 程永山 2008 计算机测量与控制 16 834
Liu X Y, Lü C M, Cheng Y S 2008 Computer Measurement & Contrl 16 834
[24] 蔡娜, 井元伟, 姜囡, 张嗣瀛 2009 东北大学学报(自然科学版) 30 313
Cai N, Jing Y W, Jiang C, Zhang S Y 2009 J. Northeast Univ. 30 313
下载:
计量
- 文章访问数: 9937
- PDF下载量: 195
- 被引次数: 0
