-
Two-dimensional magnetic material which has been rapidly developed in recent years, has potential applications in developing spintronic devices. In order to understand the magnetic properties of two-dimensional magnetic materials, it is necessary to comprehend the magnetic interaction which is estimated by the exchange parameters between the magnetic atoms. The calculation of the magnetic exchange parameters is based on the first-principle. The commonly used method of determining the values of exchange parameters is energy-mapping. However, this method has some disadvantages. In this paper, the spin-spiral dispersion relationship is derived under the Heisenberg interaction and the Dzyaloshinskii-Moriya (DM) interaction through the generalized Bloch condition of three common two-dimensional magnetic structures: a tetragonal structure, a hexagonal structure in which the cell contains one magnetic atom, a hexagonal structure in which the cell contains two magnetic atoms. The magnetic exchange parameters of some materials are calculated through the first principle. These materials are MnB, VSe 2 MnSTe and Cr 2I 3Cl 3. Among them, the MnSTe and Cr 2I 3Cl 3 are two-dimensional Janus materials, which means that they have space-reversal symmetry broken, that is why there is DM interaction in the system.
-
Keywords:
- two-dimensional magnetic structure /
- magnetic interaction /
- generalized Bloch condition /
- first principles
[1] Bi C, Liu Y H, Newhouse-Illige T, Xu M, Rosales M, Freeland J W, Mryasov O, Zhang S F, Velthuis S G E, Wang W G 2014 Phys. Rev. Lett. 113 267202
[2] Novoselov K S, Mishchenko A, Carvalho A, Castro Neto A H 2016 Science 353 9439
Google Scholar
[3] Wang Z, Gutiérrez-Lezama I, Ubrig N, Kroner M, Gibertini M, Taniguchi T, Watanabe K, Imamoğlu A, Giannini E, Morpurgo A F 2018 Nat. Commun. 9 2516
Google Scholar
[4] Hu C, Zhang D, Yan F G, Li Y C, Lv Q S, Zhu W K, Wei Z M, Chang K, Wang K Y 2020 Sci. Bull. 65 1072
Google Scholar
[5] Mermin N D, Wagner H 1966 Phys. Rev. Lett. 17 1133
Google Scholar
[6] Gong C, Li L, Li Z L, Ji H W, Stern A, Xia Y, Cao T, Bao W, Wang C Z, Wang Y, Qiu Z Q, Cava R J, Louie S G, Xia J, Zhang X 2017 Nature 546 265
Google Scholar
[7] Huang B, Clark G, Navarro-Moratalla E, Klein D R, Cheng R, Seyler K L, Zhong D, Schmidgall E, McGuire M A, Cobden D H, Yao W, Xiao D, Jarillo-Herrero P, Xu X D 2017 Nature 546 270
Google Scholar
[8] Deng Y, Yu Y, Song Y, Zhang J Z, Wang N Z, Sun Z Y, Yi Y F, Wu Y Z, Wu S W, Zhu J Y, Wang J, Chen X H, Zhang Y B 2018 Nature 563 94
Google Scholar
[9] Bonilla M, Kolekar S, Ma Y J, Diaz H C, Kalappattil V, Das R, Eggers T, Gutierrez H R, Phan M H, Batzill M 2018 Nat. Nanotechnol. 13 289
Google Scholar
[10] O'Hara D J, Zhu T, Trout A H, Ahmed A S, Luo Y Q, Lee C H, Brenner M R, Rajan S, Gupta J, McComb D W, Kawakami R K 2018 Nano. Lett. 18 3125
Google Scholar
[11] Dzyaloshinsky I 1958 J. Phys. Chem. Solids 4 241
Google Scholar
[12] Moriya T 1960 Phys. Rev. 120 91
Google Scholar
[13] Muehlbauer S, Binz B, Jonietz F, Pfleiderer C, Rosch A, Neubauer A, Georgii R, Böni P 2009 Science 323 915
Google Scholar
[14] Zhu Y, Ma C L, Shi D N, Zhang K C 2014 Phys. Lett. A 378 2234
Google Scholar
[15] Yang H X, Thiaville A, Rohart S, Fert A, Chshiev M 2015 Phys. Rev. Lett. 115 267210
Google Scholar
[16] Pan Y, Zhu Y, Shi D N, Wei X Y, Ma C L, Zhang K C 2015 J. Alloys Compd. 644 341
Google Scholar
[17] Xiang H J, Lee C, Koo H J, Gong X G 2013 Dalton Trans. 42 823
Google Scholar
[18] Marsman M, Hafner J 2002 Phys. Rev. B 66 224409
Google Scholar
[19] Sandratskii L M 1991 J. Phys. Condens. Matter 3 8565
Google Scholar
[20] Knöpfle K, Sandratskii L M, Kübler J 2000 Phys. Rev. B 62 5564
Google Scholar
[21] Hector A L, Jura M, Levason W, Reid S D, Reid G 2009 New J. Chem. 33 641
Google Scholar
[22] Kresse G, Joubert D 1999 Phys. Rev. B 59 1758
[23] Blöchl P E 1994 Phys. Rev. B 50 17953
Google Scholar
[24] Farooq M U, Hashmi A, Khan I, Hong J S 2017 Sci. Rep. 7 17101
Google Scholar
[25] Liu C, Fu B T, Yin H B, Zhang G B, Dong C 2020 Appl. Phys. Lett. 117 103101
Google Scholar
[26] Zhang J, Jia S, Kholmanov I, Dong L, Er D, Chen W B, Guo H, Jin Z H, Shenoy V B, Shi L, Lou J 2017 ACS Nano 11 8192
Google Scholar
[27] He J J, Li S 2018 Comput. Mater. Sci. 152 151
Google Scholar
[28] Xu C S, Feng J S, Prokhorenko S, Nahas Y, Xiang H J, Bellaiche L 2020 Phys. Rev. B 101 060404
Google Scholar
[29] Fert A, Cros V, Sampaio J 2013 Nat. Nanotechnol. 8 152
Google Scholar
-
图 1 奈尔型斯格明子的磁矩结构示意图
Figure 1. Spin configuration of Néel skyrmions.
图 2 VSe 2原子结构示意图 (a) 俯视图; (b) 侧视图
Figure 2. The view of the lattice structure for VSe 2: (a) Top view; (b) side view.
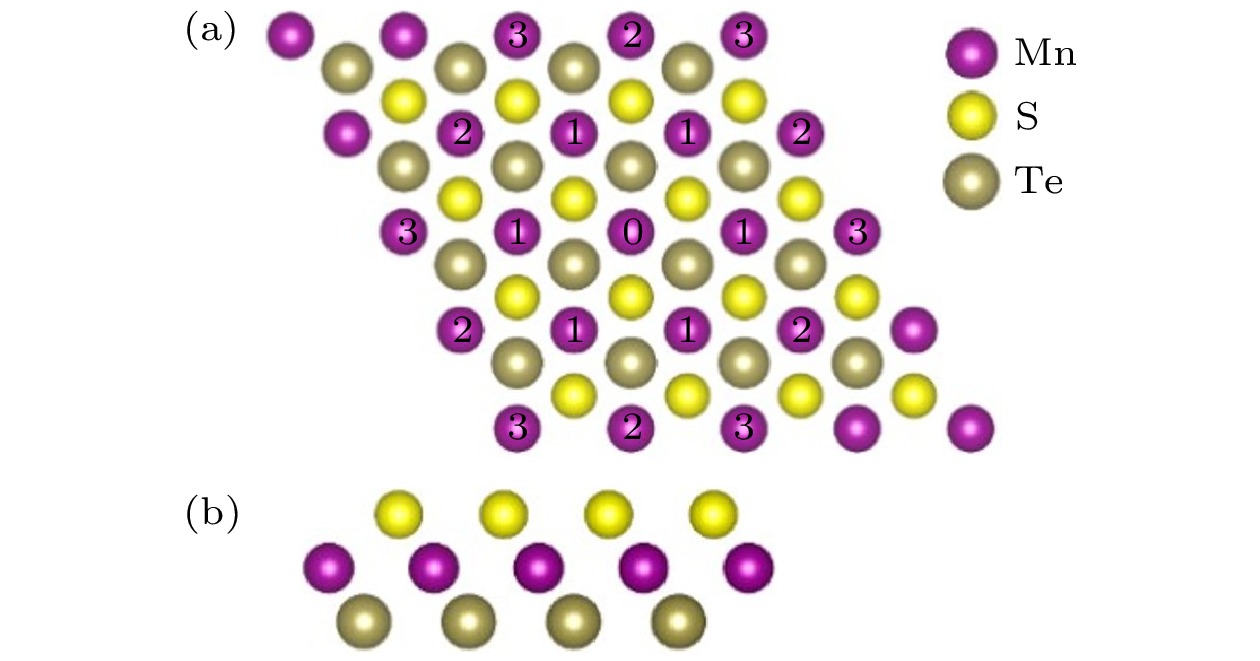
图 3 (a)六角结构的原胞基矢和倒格基矢的示意图; (b)六角结构的磁性原子及各近邻原子的分布; (c) 磁性原子的磁矩变化坐标系(蓝色坐标轴)以及二维晶格坐标系(黑色坐标轴)示意图
Figure 3. (a) The labeled a 1 and a 2 are basis vectors and b 1 and b 2 are reciprocal lattice vectors. (b) distribution of neighboring atoms; (c) blue axis and black axis represent the coordinate system of magnetic moment and two dimensional lattice , respectively.
图 4 离散点是VSe 2体系通过程序计算得到的自旋螺旋能量色散关系 E( q ), 其中 q 是自旋螺旋的波矢; 实线是拟合曲线
Figure 4. Scatter symbols are energy dispersion E( q ) as a function of the spiral wave vector q calculated by program, lines are fitted ones.
图 5 MnB原子结构示意图 (a) 俯视图; (b) 侧视图
Figure 5. Structure of MnB: (a) Vertical view; (b) side view.
图 6 离散点是MnB体系通过程序计算得到的自旋螺旋能量色散关系 E( q ), 其中 q 是自旋螺旋的波矢; 实线是拟合曲线
Figure 6. Scatter symbols are energy dispersion E( q ) of MnB as a function of the spiral wave vector q calculated by program, lines are fitted ones.
图 7 离散点是MnB体系通过程序计算得到的自旋螺旋能量色散关系 E( q ), 其中 q 是自旋螺旋的波矢; 实线是拟合曲线
Figure 7. Scatter symbols are energy dispersion E( q ) of MnB as a function of the spiral wave vector q calculated by program, lines are fitted ones.
图 8 MnSTe原子结构示意图 (a) 俯视图; (b) 侧视图
Figure 8. Atomic structure of MnSTe: (a) Vertical view; (b) side view.
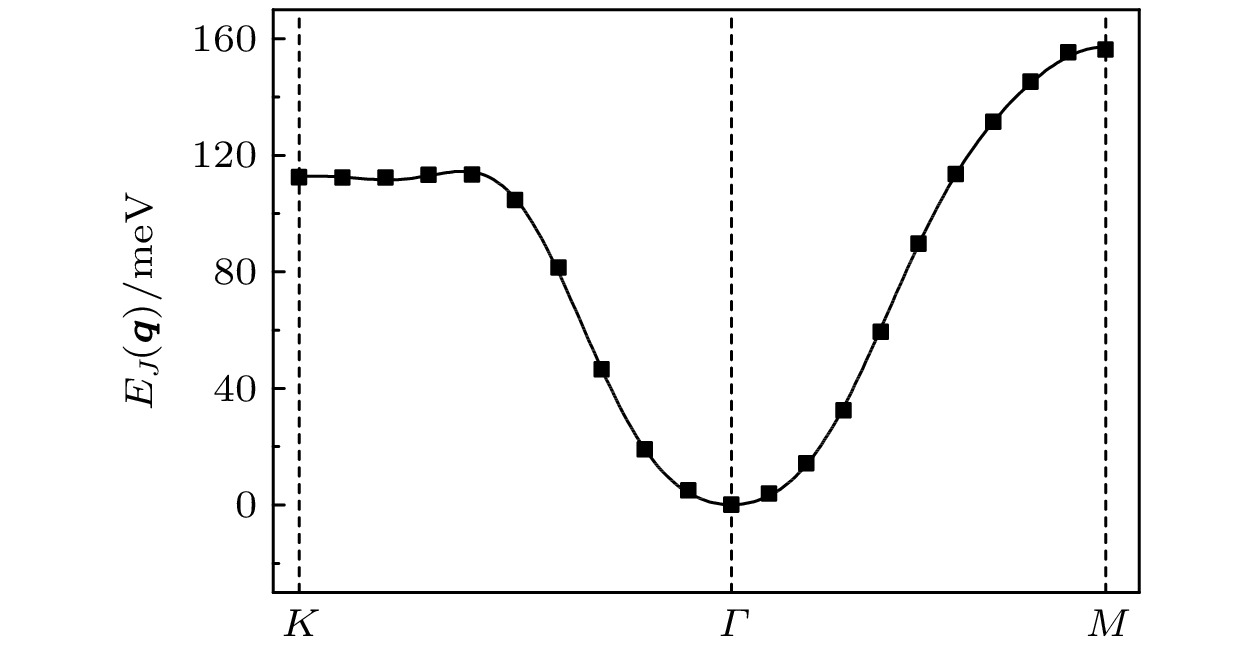
图 9 (a)离散点是MnSTe体系通过程序计算得到的自旋螺旋能量色散关系 E( q )和 E(– q ), 其中 q 是自旋螺旋的波矢, 实线是拟合曲线; (b)离散点是MnSTe体系通过程序计算的 E( q )与 E(– q )之间的能量差 E DMI( q ), 实线是拟合曲线
Figure 9. (a) Scatter symbols are energy dispersion E( q ) and E(– q ) of MnSTe as a function of the spiral wave vector q calculated by program, lines are fitted ones; (b) scatter symbols are E DMI( q ) which means the difference between E( q ) and E(– q ), lines are fitted ones.
图 10 Cr 2I 3Cl 3原子结构示意图 (a) 俯视图; (b) 侧视图
Figure 10. Atomic structure of Cr 2I 3Cl 3: (a) Vertical view; (b) side view.
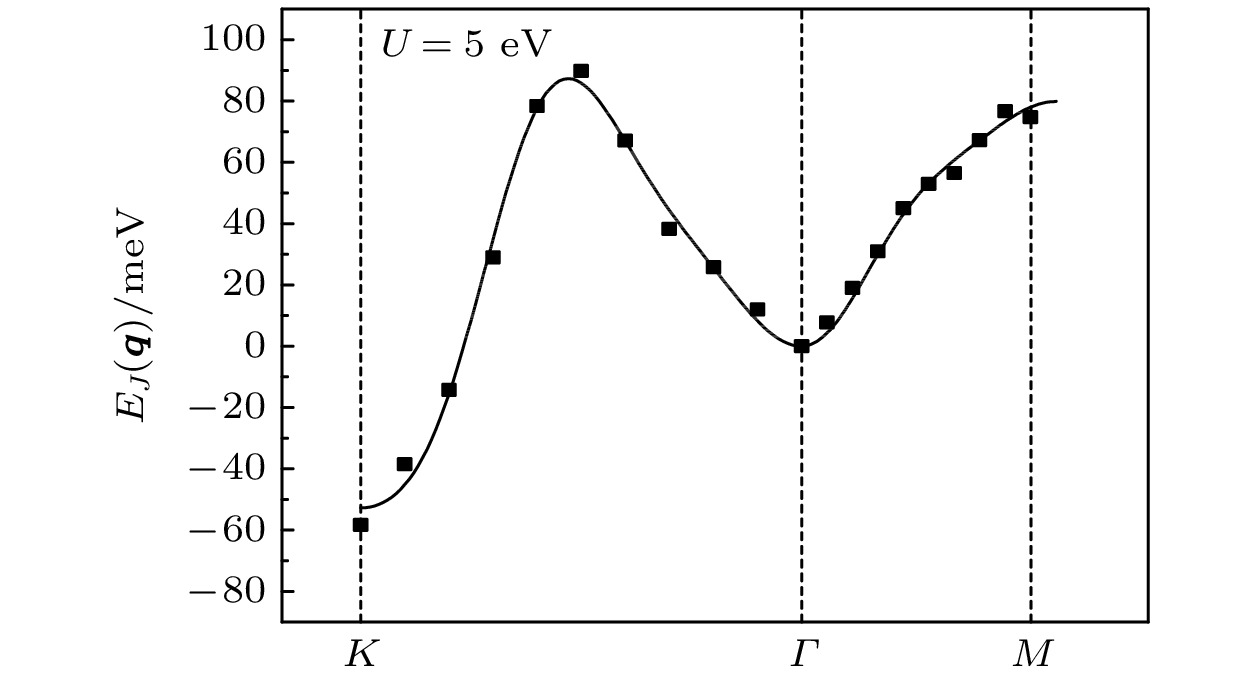
图 11 (a)离散点是Cr 2I 3Cl 3体系通过程序计算得到的自旋螺旋能量色散关系 E( q )和 E(– q ), 其中 q 是自旋螺旋的波矢, 实线是拟合曲线; (b)离散点是Cr 2I 3Cl 3体系通过程序计算的 E( q )与 E(– q )之间的能量差 E DMI( q ), 实线是拟合曲线
Figure 11. (a) Scatter symbols are energy dispersion E( q ) and E(– q ) of Cr 2I 3Cl 3 as a function of the spiral wave vector q calculated by program, lines are fitted ones; (b) scatter symbols are E DMI( q ) which means the difference between E( q ) and E(– q ), lines are fitted ones.
表 1 VSe 2结构中磁性原子各近邻的海森伯交换参数大小(单位: meV)
Table 1. Calculated parameters of Heisenberg exchange J of VSe 2, J is considered to the eighth neighbor. (The unit of J is meV).
J 1 J 2 J 3 J 4 J 5 J 6 J 7 J 8 27.24 12.81 –2.8 0.59 –1 –1.5 –0.5 0.38 
DownLoad: CSV
表 2 MnB结构( U= 3 eV)中磁性原子各近邻的海森伯交换参数大小(单位: meV)
Table 2. Calculated parameters of Heisenberg exchange J of MnB, J is considered to the eighth neighbor. (The unit of J is meV).
J 1 J 2 J 3 J 4 J 5 J 6 J 7 J 8 21.22 44.5 –2.52 –4.53 0.952 1.08 0.569 1.27
DownLoad: CSV
表 3 MnSTe结构中磁性原子各近邻的海森伯交换参数大小(单位: meV)
Table 3. Calculated parameters of Heisenberg exchange J of MnSTe, J is considered to the eighth neighbor. (The unit of J is meV).
J 1 J 2 J 3 J 4 J 5 J 6 J 7 J 8 5.49 4.64 6 –1.09 –1.32 0.765 –0.046 0.76
DownLoad: CSV
表 4 MnSTe结构中磁性原子各近邻的DM交换参数大小(单位: meV)
Table 4. Calculated parameters of DM exchange d of MnSTe, d is considered to the forth neighbor. (The unit of d is meV).
d 1 d 2 d 3 d 4 5.46 1.77 2.78 –0.248
DownLoad: CSV
表 5 Cr 2I 3Cl 3结构中磁性原子各近邻的海森伯交换参数大小(单位: meV)
Table 5. Calculated parameters of Heisenberg exchange J of Cr 2I 3Cl 3, J is considered to the eighth neighbor. (The unit of J is meV).
J 1 J 2 J 3 J 4 J 5 J 6 J 7 J 8 12.92 –0.35 2.11 3.55 –1.46 –0.67 –0.11 0.841
DownLoad: CSV
表 6 Cr 2I 3Cl 3结构中磁性原子各近邻的DM交换参数大小(单位: meV)
Table 6. Calculated parameters of DM exchange d of Cr 2I 3Cl 3, d is considered to the forth neighbor. (The unit of d is meV).
d 1 d 2 d 3 d 4 –0.88 0.378 1.04 –0.0493
DownLoad: CSV
-
[1] Bi C, Liu Y H, Newhouse-Illige T, Xu M, Rosales M, Freeland J W, Mryasov O, Zhang S F, Velthuis S G E, Wang W G 2014 Phys. Rev. Lett. 113 267202
[2] Novoselov K S, Mishchenko A, Carvalho A, Castro Neto A H 2016 Science 353 9439
Google Scholar
[3] Wang Z, Gutiérrez-Lezama I, Ubrig N, Kroner M, Gibertini M, Taniguchi T, Watanabe K, Imamoğlu A, Giannini E, Morpurgo A F 2018 Nat. Commun. 9 2516
Google Scholar
[4] Hu C, Zhang D, Yan F G, Li Y C, Lv Q S, Zhu W K, Wei Z M, Chang K, Wang K Y 2020 Sci. Bull. 65 1072
Google Scholar
[5] Mermin N D, Wagner H 1966 Phys. Rev. Lett. 17 1133
Google Scholar
[6] Gong C, Li L, Li Z L, Ji H W, Stern A, Xia Y, Cao T, Bao W, Wang C Z, Wang Y, Qiu Z Q, Cava R J, Louie S G, Xia J, Zhang X 2017 Nature 546 265
Google Scholar
[7] Huang B, Clark G, Navarro-Moratalla E, Klein D R, Cheng R, Seyler K L, Zhong D, Schmidgall E, McGuire M A, Cobden D H, Yao W, Xiao D, Jarillo-Herrero P, Xu X D 2017 Nature 546 270
Google Scholar
[8] Deng Y, Yu Y, Song Y, Zhang J Z, Wang N Z, Sun Z Y, Yi Y F, Wu Y Z, Wu S W, Zhu J Y, Wang J, Chen X H, Zhang Y B 2018 Nature 563 94
Google Scholar
[9] Bonilla M, Kolekar S, Ma Y J, Diaz H C, Kalappattil V, Das R, Eggers T, Gutierrez H R, Phan M H, Batzill M 2018 Nat. Nanotechnol. 13 289
Google Scholar
[10] O'Hara D J, Zhu T, Trout A H, Ahmed A S, Luo Y Q, Lee C H, Brenner M R, Rajan S, Gupta J, McComb D W, Kawakami R K 2018 Nano. Lett. 18 3125
Google Scholar
[11] Dzyaloshinsky I 1958 J. Phys. Chem. Solids 4 241
Google Scholar
[12] Moriya T 1960 Phys. Rev. 120 91
Google Scholar
[13] Muehlbauer S, Binz B, Jonietz F, Pfleiderer C, Rosch A, Neubauer A, Georgii R, Böni P 2009 Science 323 915
Google Scholar
[14] Zhu Y, Ma C L, Shi D N, Zhang K C 2014 Phys. Lett. A 378 2234
Google Scholar
[15] Yang H X, Thiaville A, Rohart S, Fert A, Chshiev M 2015 Phys. Rev. Lett. 115 267210
Google Scholar
[16] Pan Y, Zhu Y, Shi D N, Wei X Y, Ma C L, Zhang K C 2015 J. Alloys Compd. 644 341
Google Scholar
[17] Xiang H J, Lee C, Koo H J, Gong X G 2013 Dalton Trans. 42 823
Google Scholar
[18] Marsman M, Hafner J 2002 Phys. Rev. B 66 224409
Google Scholar
[19] Sandratskii L M 1991 J. Phys. Condens. Matter 3 8565
Google Scholar
[20] Knöpfle K, Sandratskii L M, Kübler J 2000 Phys. Rev. B 62 5564
Google Scholar
[21] Hector A L, Jura M, Levason W, Reid S D, Reid G 2009 New J. Chem. 33 641
Google Scholar
[22] Kresse G, Joubert D 1999 Phys. Rev. B 59 1758
[23] Blöchl P E 1994 Phys. Rev. B 50 17953
Google Scholar
[24] Farooq M U, Hashmi A, Khan I, Hong J S 2017 Sci. Rep. 7 17101
Google Scholar
[25] Liu C, Fu B T, Yin H B, Zhang G B, Dong C 2020 Appl. Phys. Lett. 117 103101
Google Scholar
[26] Zhang J, Jia S, Kholmanov I, Dong L, Er D, Chen W B, Guo H, Jin Z H, Shenoy V B, Shi L, Lou J 2017 ACS Nano 11 8192
Google Scholar
[27] He J J, Li S 2018 Comput. Mater. Sci. 152 151
Google Scholar
[28] Xu C S, Feng J S, Prokhorenko S, Nahas Y, Xiang H J, Bellaiche L 2020 Phys. Rev. B 101 060404
Google Scholar
[29] Fert A, Cros V, Sampaio J 2013 Nat. Nanotechnol. 8 152
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5509
- PDF Downloads: 138
- Cited By: 0
