Nonequilibrium thermal transport and thermodynamic geometry in periodically driven systems

Wang Zi; Ren Jie

doi:10.7498/aps.70.20211723

Abstract

With the in-depth understanding of nano-/micro-scaled systems and the developing of the corresponding experimental techniques, the heat transport and energy conversion processes in these small systems have attracted much interest recently. In contrast to the static manipulation methods, which hinge on the steady nonequilibrium sources such as temperature bias, chemical potential difference, etc., the temporal driving methods can control small systems in nonequilibrium non-steady states with much more versatility and universality. The research on periodically driven small systems holds both fundamental and pragmatic promises. This review is based on the fundamental concept of geometry. By analyzing the geometric phase and thermodynamic length in the transport process and the energy conversion process, we provide a unified perspective for the recent researches on the thermodynamic properties of driven nonequilibrium quantum systems. Thermodynamic geometry not only is the intrinsic origin of the nontrivial transport and dissipation, but also provides us with an all-applicable theoretical framework. The discussion over the geometry would yield multiple thermodynamic constraints on the transport and energy conversion, and can naturally construct a general optimization method as well. This will conduce to a better understanding of functionality for nonequilibrium quantum many-body systems acting as thermal machines. Also, this will inspire people to design quantum thermal machines with simultaneously more ideal performance, i.e. higher efficiency, higher power and higher constancy.

Keywords:

Authors and contacts

Wang Zi,
Ren Jie

Shanghai Key Laboratory of Special Artificial Microstructure Materials and Technology, Center for Phononics and Thermal Energy Science, China-EU Joint Lab on Nanophononics, School of Physics Science and Engineering, Tongji University, Shanghai 200092, China

Corresponding author: Ren Jie, xonics@tongji.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 11935010, 11775159).

FullText HTML : translate this paragraph

References

[1]	Martínez I A, Roldán É, Dinis L, Petrov D, Parrondo J M, Rica R A 2016 Nat. Phys. 12 67 Google Scholar
[2]	Seifert U 2008 Eur. Phys. J. B 64 423 Google Scholar
[3]	Scully M O, Zubairy M S, Agarwal G S, Walther H 2003 Science 299 862 Google Scholar
[4]	Roßnagel J, Abah O, Schmidt-Kaler F, Singer K, Lutz E 2014 Phys. Rev. Lett. 112 30602 Google Scholar
[5]	Rahav S, Harbola U, Mukamel S 2012 Phys. Rev. A 86 43843 Google Scholar
[6]	Goswami H P, Harbola U 2013 Phys. Rev. A 88 13842 Google Scholar
[7]	王子, 张丹妹, 任捷 2019 68 220302 Google Scholar Wang Z, Zhang DM, Ren J 2019 Acta Phys. Sin. 68 220302 Google Scholar
[8]	Esposito M, Lindenberg K, Van den Broeck C 2009 Phys. Rev. Lett. 102 130602 Google Scholar
[9]	Nakpathomkun N, Xu H Q, Linke H 2010 Phys. Rev. B 82 235428 Google Scholar
[10]	Tu Z C 2012 Chin. Phys. B 21 020513 Google Scholar
[11]	Van den Broeck C 2005 Phys. Rev. Lett. 95 190602 Google Scholar
[12]	Abiuso P, Perarnau-Llobet M 2020 Phys. Rev. Lett. 124 110606 Google Scholar
[13]	Miller H J, Mohammady M H, Perarnau-Llobet M, Guarnieri G 2021 Phys. Rev. Lett. 126 210603 Google Scholar
[14]	Solon A P, Horowitz J M 2018 Phys. Rev. Lett. 120 180605 Google Scholar
[15]	Ren J, Hänggi P, Li B 2010 Phys. Rev. Lett. 104 170601 Google Scholar
[16]	Nie W, Li G, Li X, Chen A, Lan Y, Zhu S 2020 Phys. Rev. A 102 43512 Google Scholar
[17]	Ren J, Liu S, Li B 2012 Phys. Rev. Lett. 108 210603 Google Scholar
[18]	Wang C, Ren J, Cao J 2017 Phys. Rev. A 95 23610 Google Scholar
[19]	Giri S K, Goswami H P 2017 Phys. Rev. E 96 052129 Google Scholar
[20]	Hino Y, Hayakawa H 2021 Phys. Rev. Res. 3 13187 Google Scholar
[21]	Yuge T, Sagawa T, Sugita A, Hayakawa H 2013 J. Stat. Phys. 153 412 Google Scholar
[22]	Sagawa T, Hayakawa H 2011 Phys. Rev. E 84 51110 Google Scholar
[23]	Crooks G E 2007 Phys. Rev. Lett. 99 100602 Google Scholar
[24]	Sivak D A, Crooks G E 2012 Phys. Rev. Lett. 108 190602 Google Scholar
[25]	Brandner K, Saito K 2020 Phys. Rev. Lett. 124 40602 Google Scholar
[26]	Miller H J, Mehboudi M 2020 Phys. Rev. Lett. 125 260602 Google Scholar
[27]	Breuer H, Petruccione F 2002 The Theory of Open Quantum Systems (New York: Oxford University Press)
[28]	Kolodrubetz M, Sels D, Mehta P, Polkovnikov A 2017 Phys. Rep. 697 1 Google Scholar
[29]	Cavina V, Mari A, Giovannetti V 2017 Phys. Rev. Lett. 119 50601 Google Scholar
[30]	Sekimoto K 1997 J. Phys. Soc. Jpn. 66 1234 Google Scholar
[31]	Berry M V 1984 Proc. R. Soc. A 392 45 Google Scholar
[32]	Thouless D J 1983 Phys. Rev. B 27 6083 Google Scholar
[33]	Deffner S, Lutz E 2011 Phys. Rev. Lett. 107 140404 Google Scholar
[34]	Seifert U 2005 Phys. Rev. Lett. 95 40602 Google Scholar
[35]	Brouwer P W 1998 Phys. Rev. B 58 R10135 Google Scholar
[36]	Splettstoesser J, Governale M, König J, Fazio R 2005 Phys. Rev. Lett. 95 246803 Google Scholar
[37]	Sinitsyn N A, Nemenman I 2007 Phys. Rev. Lett. 99 220408 Google Scholar
[38]	Esposito M, Harbola U, Mukamel S 2009 Rev. Mod. Phys. 81 1665 Google Scholar
[39]	Chen T, Wang X, Ren J 2013 Phys. Rev. B 87 144303 Google Scholar
[40]	Xu D, Cao J 2016 Front. Phys. 11 110308 Google Scholar
[41]	Wang C, Ren J, Cao J 2015 Sci. Rep. 5 11787 Google Scholar
[42]	Wang Z, Wang L, Chen J, Wang C, Ren J 2022 Front. Phys. 17 13201 Google Scholar
[43]	Hino Y, Hayakawa H 2020 Phys. Rev. E 102 012115 Google Scholar
[44]	Guéry-Odelin D, Ruschhaupt A, Kiely A, Torrontegui E, Martínez-Garaot S, Muga J G 2019 Rev. Mod. Phys. 91 45001 Google Scholar
[45]	Takahashi K, Fujii K, Hino Y, Hayakawa H 2020 Phys. Rev. Lett. 124 150602 Google Scholar
[46]	Funo K, Lambert N, Nori F, Flindt C 2020 Phys. Rev. Lett. 124 150603 Google Scholar
[47]	Hatano T, Sasa S 2001 Phys. Rev. Lett. 86 3463 Google Scholar
[48]	Weinhold F 1975 J. Chem. Phys. 63 2479 Google Scholar
[49]	Ruppeiner G 1995 Rev. Mod. Phys. 67 605 Google Scholar
[50]	Feng E H, Crooks G E 2009 Phys. Rev. E 79 012104 Google Scholar
[51]	Sivak D A, Crooks G E 2016 Phys. Rev. E 94 052106 Google Scholar
[52]	Brandner K, Saito K, Seifert U 2015 Phys. Rev. X 5 031019 Google Scholar
[53]	Brandner K, Seifert U 2016 Phys. Rev. E 93 62134 Google Scholar
[54]	Bhandari B, Alonso P T, Taddei F, von Oppen F, Fazio R, Arrachea L 2020 Phys. Rev. B 102 155407 Google Scholar
[55]	Potanina E, Flindt C, Moskalets M, Brandner K 2021 Phys. Rev. X 11 021013 Google Scholar
[56]	Tu Z 2021 Front. Phys. 16 33202 Google Scholar
[57]	Quan H, Liu Y, Sun C, Nori F 2007 Phys. Rev. E 76 031105 Google Scholar

Cited By

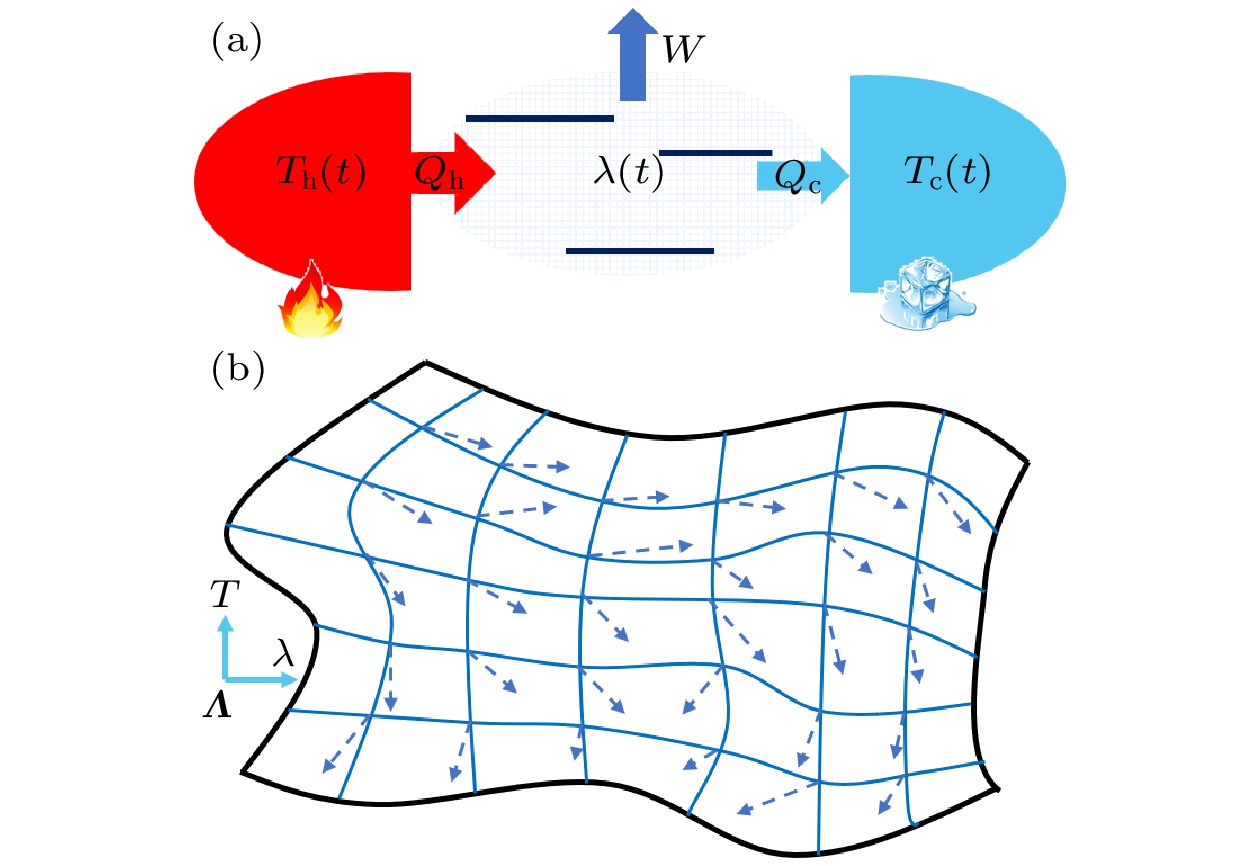
图 1 周期性驱动非平衡量子输运和其中几何性质的示意图　(a) 非平衡量子系统示意图. 量子系统由一个包含多个能级的系统来表示, 它可以与多个热库相连. 热库温度($ {T}_{\mathrm{h}} $和$ {T}_{\mathrm{c}} $)和系统参数$(\lambda)$都被含时地驱动. 由此, 可以产生系统与热库间的热量交换($ {Q}_{\mathrm{h}} $和$ {Q}_{\mathrm{c}} $)以及系统的功输出(W). (b) 此非平衡量子系统在参数空间($\boldsymbol{\varLambda }\equiv \left(T, \lambda \right) $)中的几何性质. 曲线坐标系表现出非均匀的热力学距离, 而各点的箭头表示几何联络. 几何联络在几何上对应平行移动一个微小参数时带来的和乐(holonomy)角. 热力学距离定义了一个具有度规的黎曼曲面

Figure 1. A scheme of periodically driven nonequilibrium quantum transport and its geometry. (a) A diagrammatic nonequilibrium quantum system. The middle quantum system is illustrated by a multi-level system, which is coupled with several thermal reservoirs. The temperature of reservoirs ($ {T}_{\mathrm{h}} $ and $ {T}_{\mathrm{c}} $) and the mechanical parameter of the system ($ \lambda $) are simultaneously and periodically modulated. The heat exchange ($ {Q}_{\mathrm{h}} $ and $ {Q}_{\mathrm{c}} $) and work output $(W)$ are thus generated. (b) The geometry of this nonequilibrium quantum system in the space of parameters $(\boldsymbol{\varLambda }\equiv $$ \left(T, \lambda \right) )$. The curvilinear coordinate is adopted to show the inhomogeneous thermodynamic distance and the local vectors are for the geometric connection, as derived in the main text. Geometrically, the geometric connection is the holonomy angle during an infinitesimal parallel transport and the thermodynamic distance between neighboring points defines a Riemannian space with endowed metric.

DownLoad: Full-Size Img PowerPoint

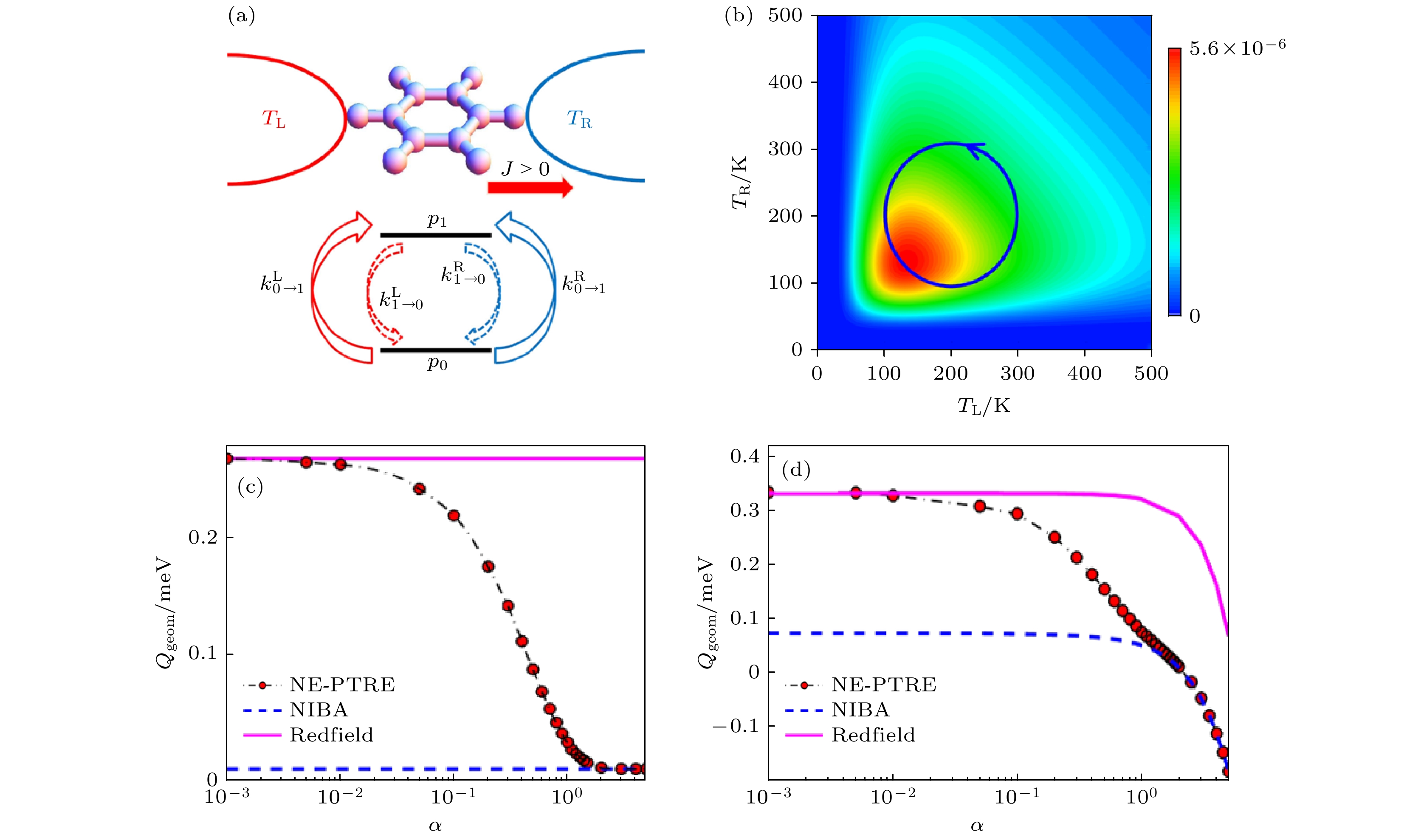
图 2 几何相热泵浦　(a) 最初研究的量子分子结系统, 工作介质由一个两能级系统描述, ${p}$和${k}$分别为各个占据数和跃迁速率^[15]; (b) 驱动两端温度产生的热泵浦现象, 图中用颜色表示了几何曲率的大小. 几何泵浦的热量为驱动回路包裹的范围内的几何曲率积分^[15]. (c), (d)自旋-玻色系统中几何相热流与系统-热库耦合强度$ \alpha $的关系^[18]. (c)为无Zeeman劈裂能的情形; (d)为有Zeeman劈裂能的情形^[18]. (a), (b)改编自文献[15]; (c), (d)改编自文献[18]

Figure 2. The geometric heat pump effect. (a) The originally studied quantum molecular junction system. The working medium is described by a quantum two-level system, with ${p}$ and ${k}$ denoting different populations and transition rates^[15]. (b) The geometric curvature in the two-temperature parameter space. The color denotes the magnitude of the geometric curvature. The pumped heat is the integral of geometric curvature over the encircled area^[15]. (c), (d) The geometrically pumped heat versus the coupling strength between the middle system and reservoirs in a quantum spin-boson system^[18]. (c) is for the setup with no Zeeman splitting while the splitting is present in (d) ^[18]. (a), (b) are adapted from [15], while (c), (d) are adapted from [18].

DownLoad: Full-Size Img PowerPoint

图 3 通过热力学距离对慢驱动热机的限制和优化　(a) 周期驱动量子热机中的功率与效率权衡. 灰色区域是根据热力学几何得出的不可能区域, 黑色线对应等速率驱动方式, 而橙色线对应经过优化的驱动方式(驱动速度随时间变化), 这两种驱动方式中驱动速度的具体形式由图(b)给出^[25]. (c), (d) 对于驱动量子热机(一个谐振子)的多目标优化^[26]　 (c)不同的优化后的驱动速度; (d) 功的相对涨落与谐振子频率的关系, 此时为效率-功涨落的多目标优化. 红线为匀速率的驱动, 而蓝线对应优化后的驱动, 灰色区域为由热力学几何给出的不可能区域^[26]. (a), (b)改编自文献[25]; (c), (d)改编自文献[26]

Figure 3. The constraint on and optimization of slowly driven quantum heat engine using the thermodynamics distance method: (a) The efficiency-power tradeoff in driven quantum heat engine. The gray area is ruled out by the thermodynamic geometry, with the black and orange line corresponding to the constant-speed driving and optimized driving protocols (driving speed is time dependent) respectively. The driving speed in these two protocols is illustrated in Figure (b)^[25]. (c), (d) A multiple target optimization of a driven heat engine composed of a harmonic oscillator: (c) the driving speed of the optimization result with different targets^[26]; (d) the relative work fluctuation versus the oscillator’s frequency (system’s parameter) with a multiple target optimization. The red line is for the constant speed driving while the blue one is for the optimized protocol. The gray area is prohibited by the thermodynamic geometry^[26]. (a), (b) are adapted from Ref. [25], while (c), (d) are adapted from Ref. [26].

DownLoad: Full-Size Img PowerPoint

map

[1]	Martínez I A, Roldán É, Dinis L, Petrov D, Parrondo J M, Rica R A 2016 Nat. Phys. 12 67 Google Scholar
[2]	Seifert U 2008 Eur. Phys. J. B 64 423 Google Scholar
[3]	Scully M O, Zubairy M S, Agarwal G S, Walther H 2003 Science 299 862 Google Scholar
[4]	Roßnagel J, Abah O, Schmidt-Kaler F, Singer K, Lutz E 2014 Phys. Rev. Lett. 112 30602 Google Scholar
[5]	Rahav S, Harbola U, Mukamel S 2012 Phys. Rev. A 86 43843 Google Scholar
[6]	Goswami H P, Harbola U 2013 Phys. Rev. A 88 13842 Google Scholar
[7]	王子, 张丹妹, 任捷 2019 68 220302 Google Scholar Wang Z, Zhang DM, Ren J 2019 Acta Phys. Sin. 68 220302 Google Scholar
[8]	Esposito M, Lindenberg K, Van den Broeck C 2009 Phys. Rev. Lett. 102 130602 Google Scholar
[9]	Nakpathomkun N, Xu H Q, Linke H 2010 Phys. Rev. B 82 235428 Google Scholar
[10]	Tu Z C 2012 Chin. Phys. B 21 020513 Google Scholar
[11]	Van den Broeck C 2005 Phys. Rev. Lett. 95 190602 Google Scholar
[12]	Abiuso P, Perarnau-Llobet M 2020 Phys. Rev. Lett. 124 110606 Google Scholar
[13]	Miller H J, Mohammady M H, Perarnau-Llobet M, Guarnieri G 2021 Phys. Rev. Lett. 126 210603 Google Scholar
[14]	Solon A P, Horowitz J M 2018 Phys. Rev. Lett. 120 180605 Google Scholar
[15]	Ren J, Hänggi P, Li B 2010 Phys. Rev. Lett. 104 170601 Google Scholar
[16]	Nie W, Li G, Li X, Chen A, Lan Y, Zhu S 2020 Phys. Rev. A 102 43512 Google Scholar
[17]	Ren J, Liu S, Li B 2012 Phys. Rev. Lett. 108 210603 Google Scholar
[18]	Wang C, Ren J, Cao J 2017 Phys. Rev. A 95 23610 Google Scholar
[19]	Giri S K, Goswami H P 2017 Phys. Rev. E 96 052129 Google Scholar
[20]	Hino Y, Hayakawa H 2021 Phys. Rev. Res. 3 13187 Google Scholar
[21]	Yuge T, Sagawa T, Sugita A, Hayakawa H 2013 J. Stat. Phys. 153 412 Google Scholar
[22]	Sagawa T, Hayakawa H 2011 Phys. Rev. E 84 51110 Google Scholar
[23]	Crooks G E 2007 Phys. Rev. Lett. 99 100602 Google Scholar
[24]	Sivak D A, Crooks G E 2012 Phys. Rev. Lett. 108 190602 Google Scholar
[25]	Brandner K, Saito K 2020 Phys. Rev. Lett. 124 40602 Google Scholar
[26]	Miller H J, Mehboudi M 2020 Phys. Rev. Lett. 125 260602 Google Scholar
[27]	Breuer H, Petruccione F 2002 The Theory of Open Quantum Systems (New York: Oxford University Press)
[28]	Kolodrubetz M, Sels D, Mehta P, Polkovnikov A 2017 Phys. Rep. 697 1 Google Scholar
[29]	Cavina V, Mari A, Giovannetti V 2017 Phys. Rev. Lett. 119 50601 Google Scholar
[30]	Sekimoto K 1997 J. Phys. Soc. Jpn. 66 1234 Google Scholar
[31]	Berry M V 1984 Proc. R. Soc. A 392 45 Google Scholar
[32]	Thouless D J 1983 Phys. Rev. B 27 6083 Google Scholar
[33]	Deffner S, Lutz E 2011 Phys. Rev. Lett. 107 140404 Google Scholar
[34]	Seifert U 2005 Phys. Rev. Lett. 95 40602 Google Scholar
[35]	Brouwer P W 1998 Phys. Rev. B 58 R10135 Google Scholar
[36]	Splettstoesser J, Governale M, König J, Fazio R 2005 Phys. Rev. Lett. 95 246803 Google Scholar
[37]	Sinitsyn N A, Nemenman I 2007 Phys. Rev. Lett. 99 220408 Google Scholar
[38]	Esposito M, Harbola U, Mukamel S 2009 Rev. Mod. Phys. 81 1665 Google Scholar
[39]	Chen T, Wang X, Ren J 2013 Phys. Rev. B 87 144303 Google Scholar
[40]	Xu D, Cao J 2016 Front. Phys. 11 110308 Google Scholar
[41]	Wang C, Ren J, Cao J 2015 Sci. Rep. 5 11787 Google Scholar
[42]	Wang Z, Wang L, Chen J, Wang C, Ren J 2022 Front. Phys. 17 13201 Google Scholar
[43]	Hino Y, Hayakawa H 2020 Phys. Rev. E 102 012115 Google Scholar
[44]	Guéry-Odelin D, Ruschhaupt A, Kiely A, Torrontegui E, Martínez-Garaot S, Muga J G 2019 Rev. Mod. Phys. 91 45001 Google Scholar
[45]	Takahashi K, Fujii K, Hino Y, Hayakawa H 2020 Phys. Rev. Lett. 124 150602 Google Scholar
[46]	Funo K, Lambert N, Nori F, Flindt C 2020 Phys. Rev. Lett. 124 150603 Google Scholar
[47]	Hatano T, Sasa S 2001 Phys. Rev. Lett. 86 3463 Google Scholar
[48]	Weinhold F 1975 J. Chem. Phys. 63 2479 Google Scholar
[49]	Ruppeiner G 1995 Rev. Mod. Phys. 67 605 Google Scholar
[50]	Feng E H, Crooks G E 2009 Phys. Rev. E 79 012104 Google Scholar
[51]	Sivak D A, Crooks G E 2016 Phys. Rev. E 94 052106 Google Scholar
[52]	Brandner K, Saito K, Seifert U 2015 Phys. Rev. X 5 031019 Google Scholar
[53]	Brandner K, Seifert U 2016 Phys. Rev. E 93 62134 Google Scholar
[54]	Bhandari B, Alonso P T, Taddei F, von Oppen F, Fazio R, Arrachea L 2020 Phys. Rev. B 102 155407 Google Scholar
[55]	Potanina E, Flindt C, Moskalets M, Brandner K 2021 Phys. Rev. X 11 021013 Google Scholar
[56]	Tu Z 2021 Front. Phys. 16 33202 Google Scholar
[57]	Quan H, Liu Y, Sun C, Nori F 2007 Phys. Rev. E 76 031105 Google Scholar

[1]	Hu Min-Li, Fang Fan, Fan Qun-Chao, Fan Zhi-Xiang, Li Hui-Dong, Fu Jia, Xie Feng. Theoretical study on macroscopic thermodynamic properties of NO⁺ ion system. Acta Physica Sinica, 2023, 72(16): 165101. doi: 10.7498/aps.72.20230541
[2]	Zhai Hui. Non-equilibrium quantum many-body physics with ultracold atoms. Acta Physica Sinica, 2023, 72(23): 230701. doi: 10.7498/aps.72.20231375
[3]	Cai Zi. Symmetries and effect of time dimension in non-equilibrium quantum matter. Acta Physica Sinica, 2021, 70(23): 230310. doi: 10.7498/aps.70.20211741
[4]	. . Acta Physica Sinica, 2021, 70(23): 230101. doi: 10.7498/aps.70.230101
[5]	Shen Jue, Liu Cheng-Zhou, Zhu Ning-Ning, Tong Yi-Nuo, Yan Chen-Cheng, Xue Ke-Lei. Thermodynamics and its quantum correction of non-commutative Schwarichild black hole. Acta Physica Sinica, 2019, 68(20): 200401. doi: 10.7498/aps.68.20191054
[6]	Wang Zi, Zhang Dan-Mei, Ren Jie. Topological and non-reciprocal phenomena in elastic waves and heat transport of phononic systems. Acta Physica Sinica, 2019, 68(22): 220302. doi: 10.7498/aps.68.20191463
[7]	Zhao Li-Mei, Zhang Guo-Feng. Entangled quantum Otto and quantum Stirling heat engine based on two-spin systems with Dzyaloshinski-Moriya interaction. Acta Physica Sinica, 2017, 66(24): 240502. doi: 10.7498/aps.66.240502
[8]	Wang Tao, Huang Xiao-Li, Liu Yang, Xu Huan. Entangled quantum heat engines based on two-qubit XXZ model with Dzyaloshinski-Mariya interaction. Acta Physica Sinica, 2013, 62(6): 060301. doi: 10.7498/aps.62.060301
[9]	Wang Jian-Hui, Xiong Shuang-Quan, He Ji-Zhou, Liu Jiang-Tao. Performance analysis of a quantum heat engine working with a particle in a one-dimensional harmonic trap. Acta Physica Sinica, 2012, 61(8): 080509. doi: 10.7498/aps.61.080509
[10]	Shen Hui-Chuan. Application of analytical thermodynamics: relativistic transformation of temperature in equilibrium thermodynamics. Acta Physica Sinica, 2005, 54(6): 2482-2488. doi: 10.7498/aps.54.2482
[11]	Wang Gang-Zhu, Wang Ji-Long. Quantum thermodynamical properties of the slowly changing nonstationary Kerr-Newman black hole. Acta Physica Sinica, 2004, 53(6): 1669-1674. doi: 10.7498/aps.53.1669
[12]	GAO TAO, WANG HONG-YAN, YI YOU-GEN, TAN MING-LIANG, ZHU ZHENG-HE, SUN YING, WANG XIAO-LIN, FU YI-BEI. ab initio CALCULATION OF THE POTENTIAL ENERGY FUNCTION AND THERMODYNAMIC FUNCTIONS FOR GROUND STATE X5Σ- OF PuO. Acta Physica Sinica, 1999, 48(12): 2222-2227. doi: 10.7498/aps.48.2222
[13]	LI BO-ZANG, ZHANG DE-GANG, WU JIAN-HUA, YAN FENG-LI. BLOCH THEOREM FOR THE EVOLUTION OF STATES IN THE CYCLIC QUANTUM SYSTEMS AND THE UNIFICATION OF RESONANT GEOMETRIC PHASES. Acta Physica Sinica, 1997, 46(2): 227-237. doi: 10.7498/aps.46.227
[14]	ZHANG WEN-ZHONG, WANG SHUN-JIN. AN ALGEBRAIC DYNAMICS APPROACH TO THE SOLUTION OF THE SU(3)LINEAR NONAUTONOMOUS QUANTUM SYSTEM. Acta Physica Sinica, 1997, 46(2): 209-226. doi: 10.7498/aps.46.209
[15]	Zuo Wei, Wang Shun-Jin. . Acta Physica Sinica, 1995, 44(9): 1363-1372. doi: 10.7498/aps.44.1363
[16]	Zuo Wei, Wang Shun-Jin. . Acta Physica Sinica, 1995, 44(8): 1177-1183. doi: 10.7498/aps.44.1177
[17]	Zuo Wei, Wang Shun-Jin, A.Weiguny, Li Fu-Li. . Acta Physica Sinica, 1995, 44(8): 1184-1191. doi: 10.7498/aps.44.1184
[18]	OU FA. . Acta Physica Sinica, 1995, 44(10): 1541-1550. doi: 10.7498/aps.44.1541
[19]	XIONG YUAN-SHENG, YI LIN, YAO KAI-LUN. THERMODYNAMIC PROPERTIES OF QUANTUM SHERRI-NGTON-KIRKPATRICK SPIN GLASS MODEL——ANISOTROPY AND MAGNETIC EFFECTS. Acta Physica Sinica, 1994, 43(12): 2052-2058. doi: 10.7498/aps.43.2052
[20]	DU YI-JING, CHEN LI-RONG, YAN ZU-TONG. THE THERMODYNAMIC PROPERTIES OF TWO-DIMENSIONAL SYSTEM. Acta Physica Sinica, 1982, 31(7): 939-944. doi: 10.7498/aps.31.939

Catalog

Vol. 70, Issue 23 - 2021-12-05

Metrics

Abstract views: 5872
PDF Downloads: 300
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板