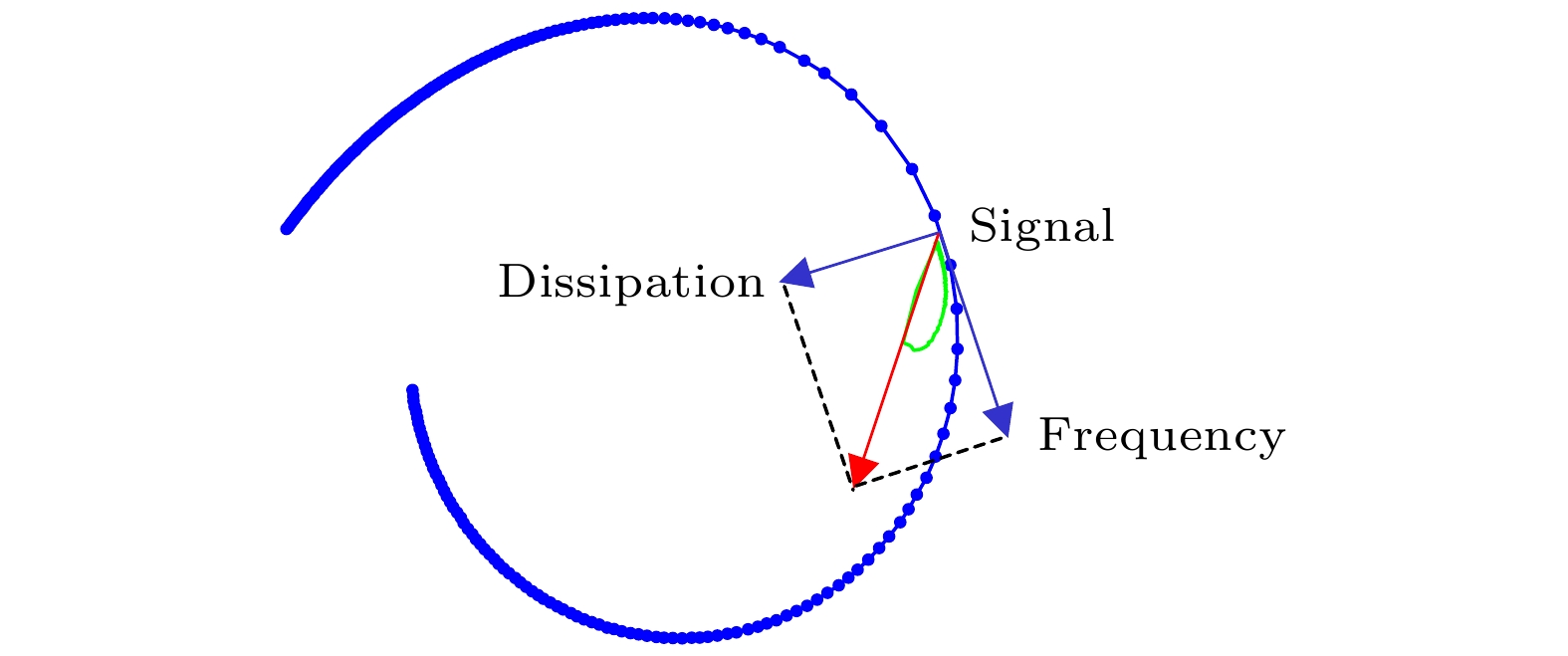
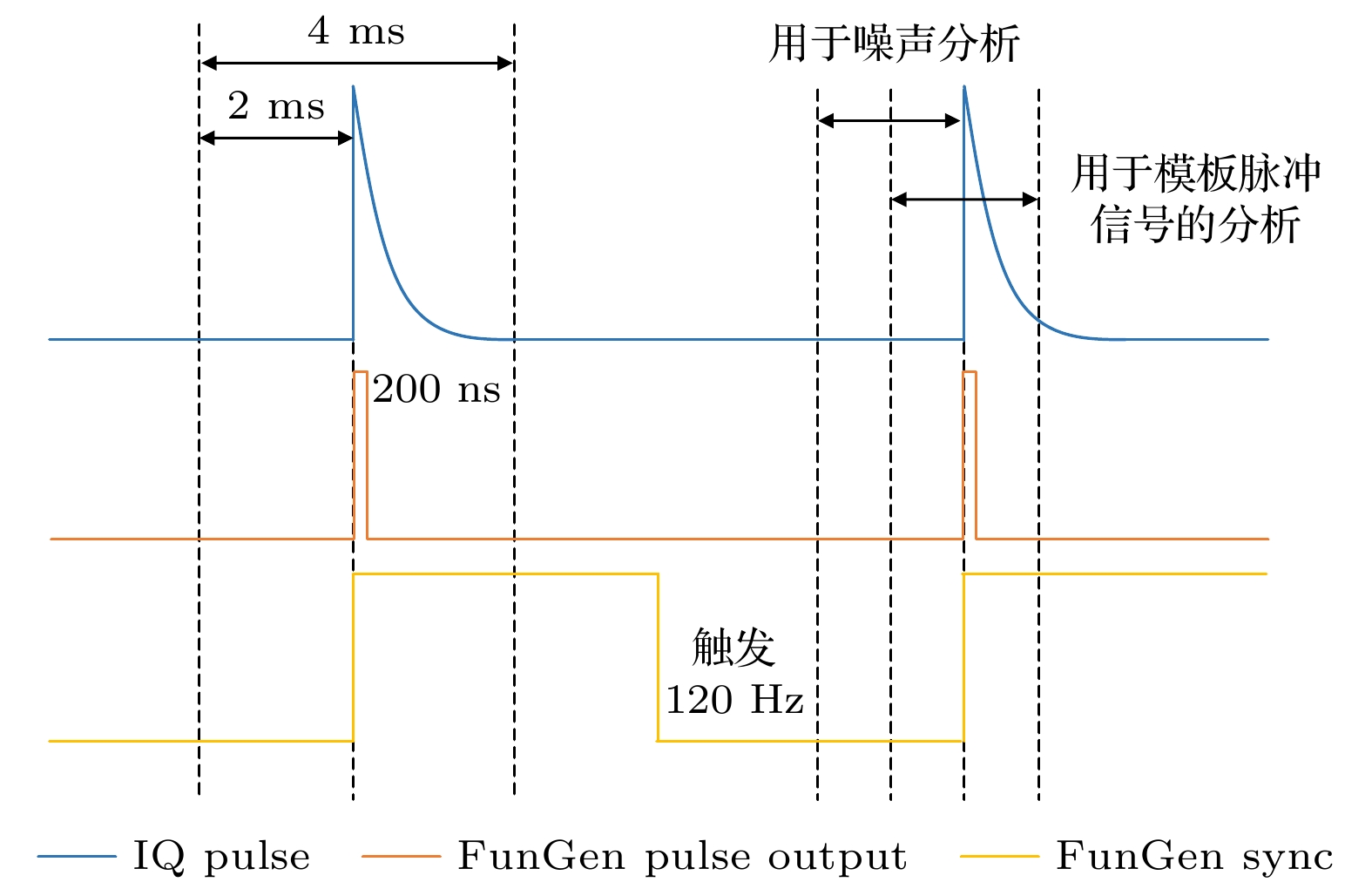
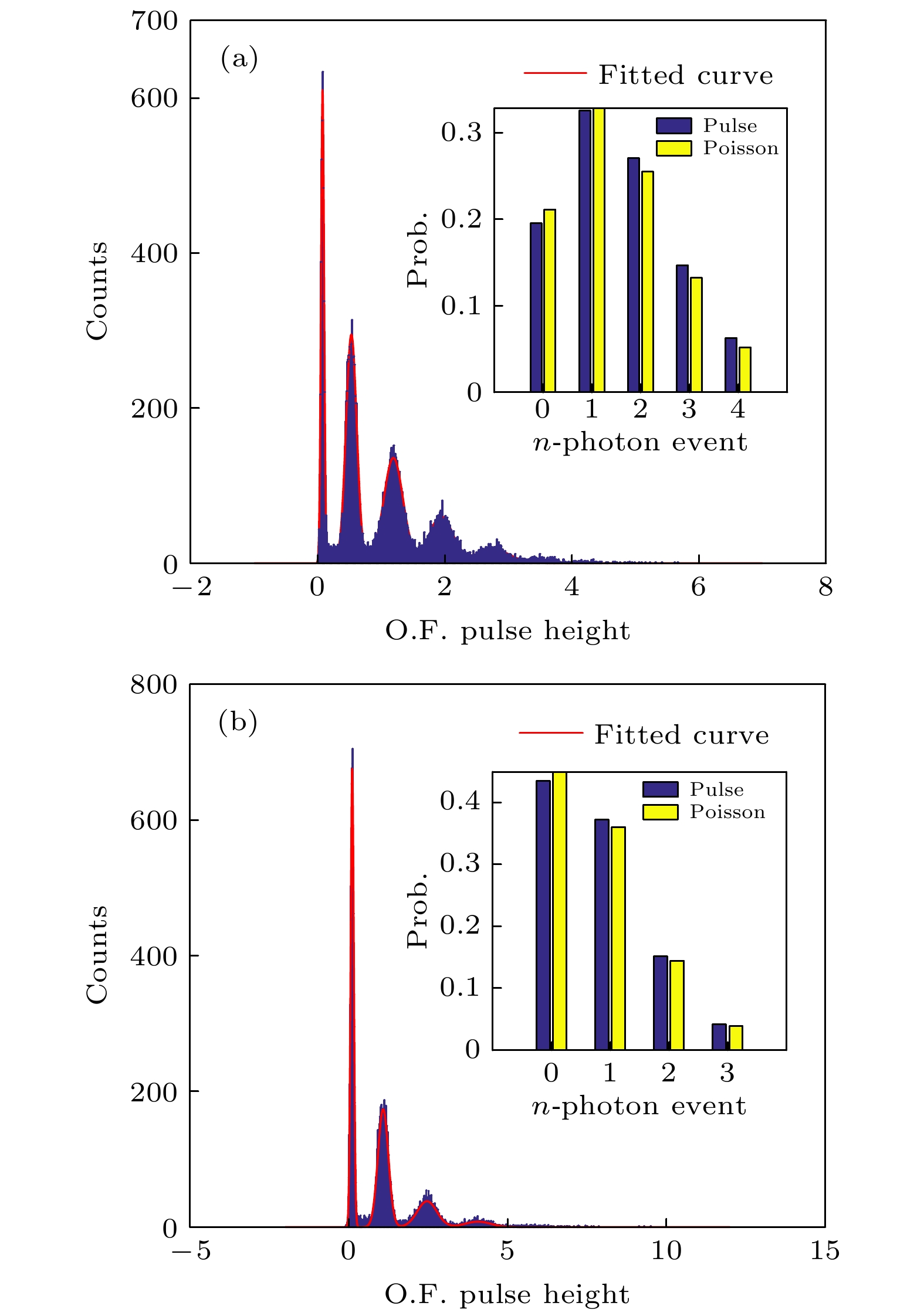
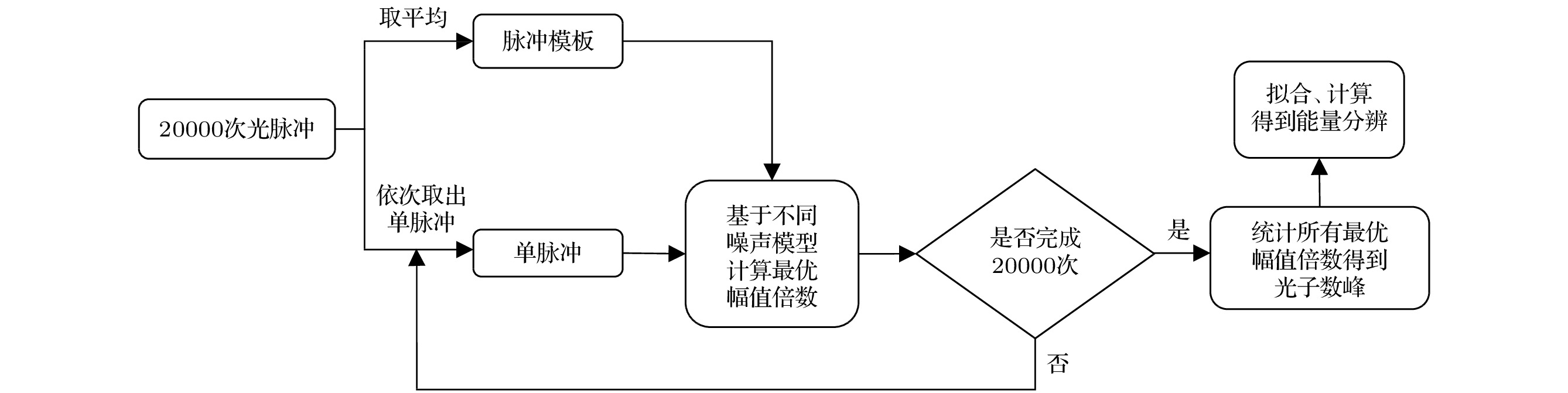
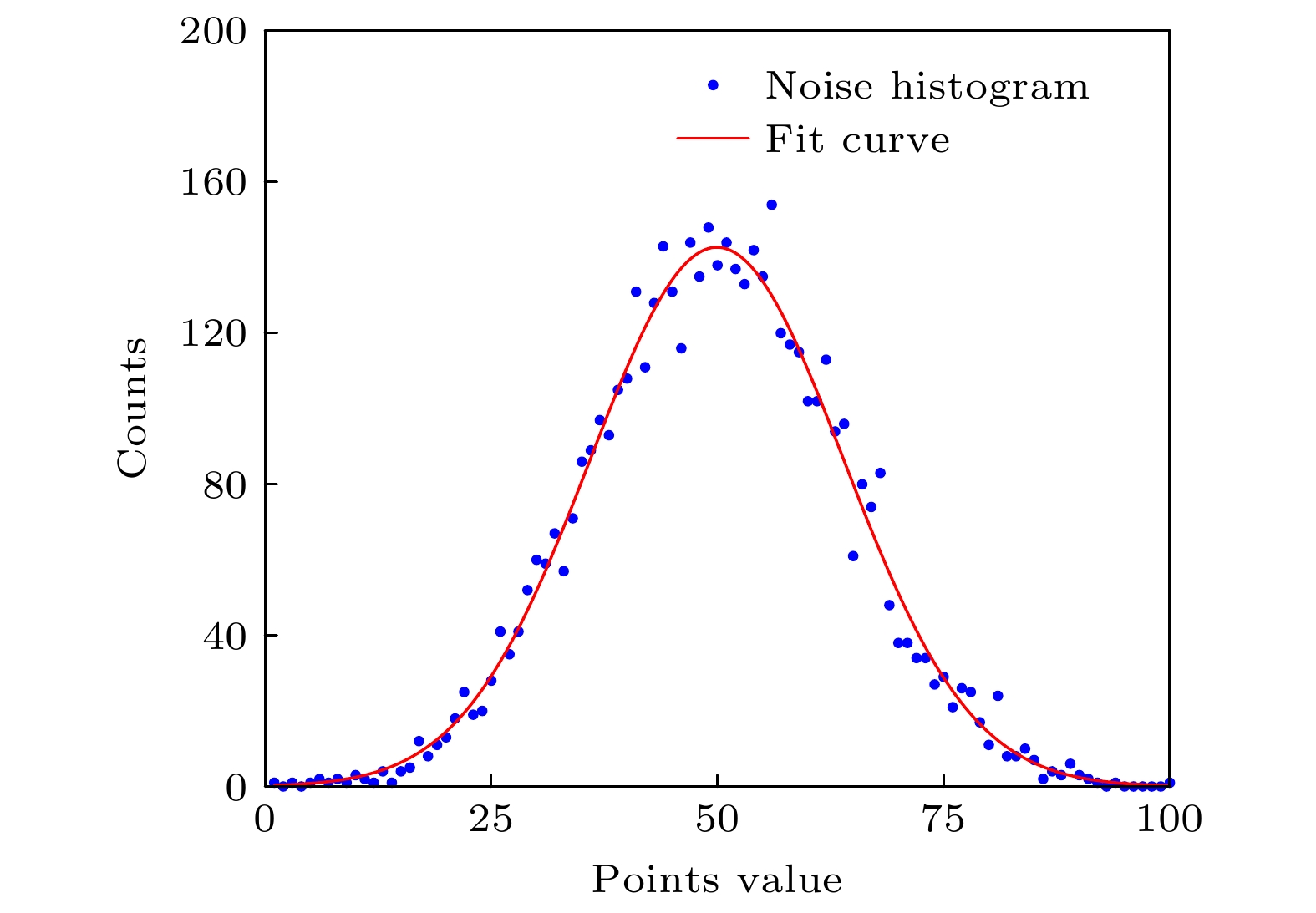
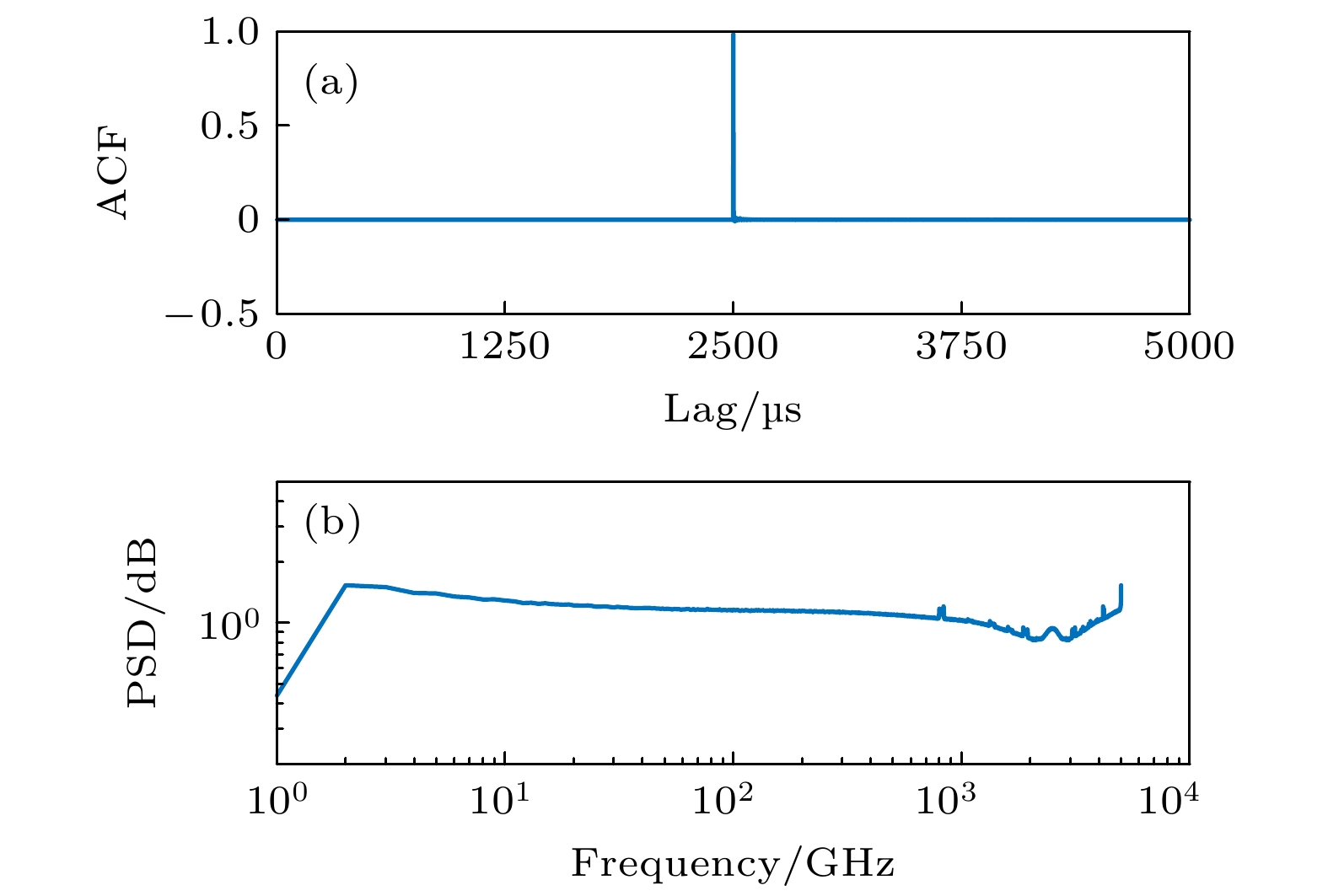
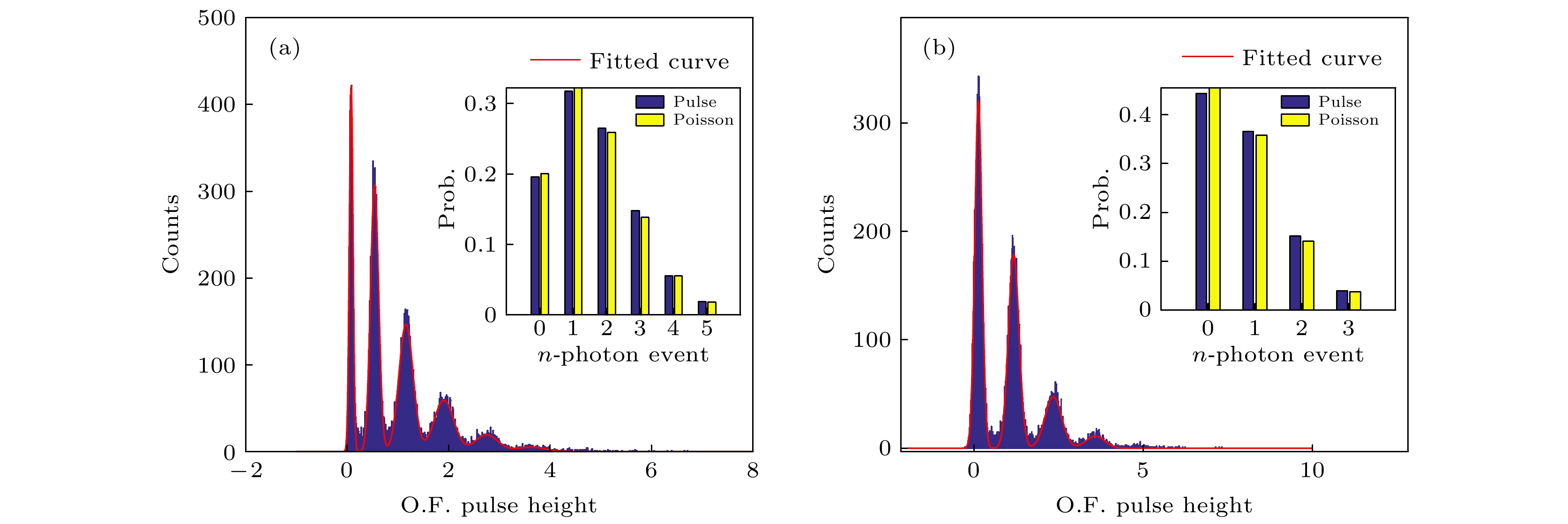
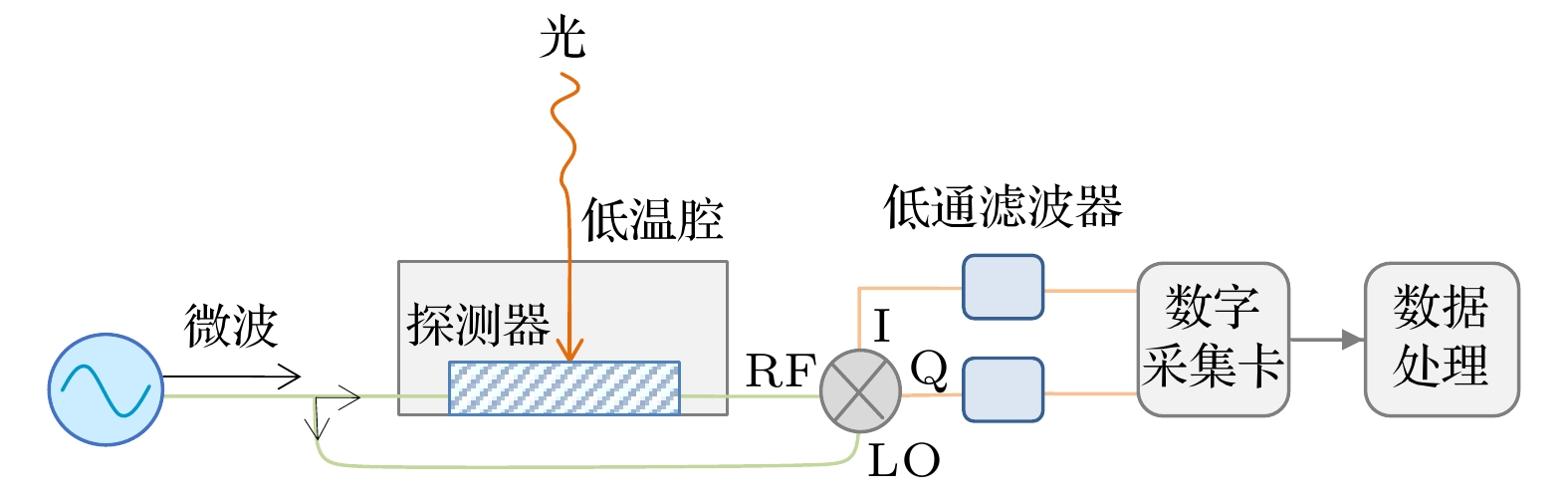
-
Noise is one of the main factors affecting the performance index of weak signal detection devices, and the optimal filtering algorithm is an effective method to adaptively extract various useful weak signals from the white noise background. In order to improve the performance of single photon detector (especially the photon number resolution ability), one mainly focuses on the optimization of detector hardware such as the optimization of photosensitive materials and the technology of device fabrication. However, in this paper the performance of microwave kinetic Inductance detector (MKID) in the way of data processing is improved. Considering the fact that the template of light pulse signal in the optimal filtering algorithm is obtained by taking the average, we replace the noise model in the original optimal filtering algorithm with the white noise model and the whitening noise model. Then we process the photon response data that are detected by the MKID in an extremely low temperature environment. The results show that the energy resolution (one of the main performance indexes of single photon detector) of MKID is improved by about 15%, and we achieve an infrared single photon energy resolution of 0.26 eV. In this paper, the application and development trends of superconducting single photon detector are briefed. Then, how the MKID responds to weak coherent optical signal in low temperature environment, and the process of signal conversion, acquisition and output are explained in detail. According to the optimal filtering algorithm, we use different noise models to analyze the results of the signals detected by MKID. After that, we count the optimal amplitude multiple, perform the Gaussian fitting analysis on the statistical graph, and compare the energy resolution with the photon number resolution of the optimal filtering algorithm under different noise models. As a result, we find that under the white noise model, the optimal filtering algorithm is used to obtain the best result for MKID processing, and high energy resolution can be achieved.
-
Keywords:
- optimal filtering /
- microwave kinetic inductance detector /
- energy resolution /
- noise model
[1] Hiskett P A, Lita A E, Hughes R J, Rosenberg D, Miller A J, Nordholt J E, Peterson C G, Nam S 2006 New J. Phys. 8 193
Google Scholar
[2] Knill E, Laflamme R, Milburn G J 2001 Nature 409 46
Google Scholar
[3] Zwinkels J C, Ikonen E, Fox N P, Ulm G, Rastello ML 2010 Metrologia 47 R15
Google Scholar
[4] 周品嘉 2014 博士学位论文 (成都: 西南交通大学)
Zhou P J 2014 Ph. D. Dissertation (ChengDu: Southwest Jiaotong University) (in Chinese)
[5] Enss C 2005 Cryogenic Particle Detection 1 (Berlin: Springer-Verlag) pp417−452
[6] Zheng F, Xu R, Zhu G, Jin B, Kang L, Xu W, Chen J, Wu P 2016 Sci. Rep. 6 22710
Google Scholar
[7] 张青雅, 董文慧, 何根芳, 李铁夫, 刘建设, 陈炜 2014 63 200303
Google Scholar
Zhang Q Y, Dong W H, He G F, Li T F, Liu J S, Chen W 2014 Acta Phys. Sin. 63 200303
Google Scholar
[8] Day P K, Leduc H G, Mazin B A, Vayonakis A, Zmuidzinas J 2003 Nature 425 817
Google Scholar
[9] 李春光, 王佳, 吴云, 王旭, 孙亮, 董慧, 高波, 李浩, 尤立星, 林志荣, 任洁, 李婧, 张文, 贺青, 王轶文, 韦联福, 孙汉聪, 王华兵, 李劲劲, 屈继峰 2021 70 018501
Google Scholar
Li C G, Wang J, Wu Y, Wang X, Sun L, Dong H, Gao B, Li H, You L X, Lin Z R, Ren J, Li J, Zhang W, He Q, Wang Y W, Wei L F, Sun H C, Wang H B, Li J J, Qu J F 2021 Acta Phys. Sin. 70 018501
Google Scholar
[10] 周品嘉, 王轶文, 韦联福 2014 63 070701
Google Scholar
Zhou P J, Wang Y W, Wei L F 2014 Acta Phys. Sin. 63 070701
Google Scholar
[11] Lita A E, Miller A J, Nam S W 2008 Opt. Express 16 3032
Google Scholar
[12] Lolli L, Taralli E, Portesi C, Monticone E, Rajteri M 2013 Appl. Phys. Lett. 103 041107
Google Scholar
[13] Yang X Y, Li H, Zhang W J, You L X, Zhang L, L iu, X Y, Wang Z, Peng W, Xie X M, Jiang M H 2014 Opt. Express 22 16267
Google Scholar
[14] Li X, Tan J R, Zheng K M, Zhang L B, Zhang J L, He W J, Huang P W, Li H C, Zhang B, Chen Q, Ge R, Guo S Y, Huang T, Jia X Q, Zhao Q Y, Tu X C, Kang L, Chen J, Wu P H 2020 Photonics Research 8 637
Google Scholar
[15] Geng Y, Zhang W, Li P Z, Zhong J Q, Wang Z, Miao W, Ren Y, Wang J F, Yao Q J, Shi S C 2020 J. Low Temp. Phys. 199 556
Google Scholar
[16] Guo W, Liu X, Wang Y, Wei Q, Wei L F, Hubmayr J, Fowler J, Ullom J, Vale L, Vissers M R, Gao J 2017 Appl. Phys. Lett. 110 212601
Google Scholar
[17] Liu X, Guo W, Wang Y, Dai M, Wei L F, Dober B, McKenney C M, Hilton G C, Hubmay J, Austermann J E, Ullom J N, Gao J, Ullom J N 2017 Appl. Phys. Lett. 111 252601
Google Scholar
[18] Szymkowiak A E, Kelley R L, Moseley S H, Stahle C K 1993 J. Low Temp. Phys. 93 281
Google Scholar
[19] Lindeman M A 2000 Ph. D. Dissertation (Davis, California: University of California at Davis)
[20] Anderson B D O, Moore J B 1979 Optimal Filtering (Upper Saddle River: Prentice Hall) pp417−421
[21] Walls D F, Milburn G 2008 Quantum Optics (2nd Ed.) (Berlin: Springer-Verlag) pp46−48
[22] Irwin K D 1995 Ph. D. Dissertation (Palo Alto, California: Stanford University)
[23] Wang L L, Li J, Yang N, Li X 2019 New J. Phys. 21 043005
Google Scholar
[24] 张贤达 2013 矩阵分析与应用 (第2版) (北京: 清华大学出版社) 第502−508页
Zhang X D 2013 Matrix analysis and Application (2nd Ed.) (Beijing: Tsinghua University Press) pp502−508 (in Chinese)
[25] Alpert B K, Horansky R D, Bennett D A, Doriese W B, Fowler J W, Hoover A S, Rabin M W, Ullom J N 2013 Rev. Sci. Instrum. 84 056107
Google Scholar
-
图 1 实验测量系统示意图
Figure 1. Schematic diagram of the experimental system for single-photon detection.
图 2 复平面上的脉冲响应图
Figure 2. Pulse response diagram.
图 3 触发模式记录时间序列信号的示意图
Figure 3. Schematic diagram of the signal triggers and records in time domain.
图 4 实验测量的探测器噪声 (a)自相关函数; (b)功率谱密度
$ J\left(f\right) $ Figure 4. Autocorrelation function (a) and power spectral density(b) of detector noise measured experimentally.
图 5 光学衰减17 dB (a)和20 dB (b)下脉冲信号幅值统计的高斯拟合结果
Figure 5. Gaussian fitting results of pulse signal amplitudes under optical attenuation of 17 dB (a) and 20 dB (b), respectively, for the experimental noises.
图 6 信号处理的流程框图
Figure 6. Flow diagram of the signal processing.
图 7 探测器噪声(点集)及其高斯分布函数拟合(红实线)
Figure 7. Detector noise (point set) and Gaussian distribution function fitting (red solid line).
图 8 采用白噪声模型后, 光学衰减17 dB (a)和20 dB (b)下的脉冲幅值统计分布以及拟合图像
Figure 8. Gaussian fitting results of pulse signal amplitudes under optical attenuation of 17 dB (a) and 20 dB (b), respectively, for the ideal white noises.
图 9 白化后的探测器噪声 (a)自相关函数; (b)功率谱密度
$ J{'}\left(f\right) $ Figure 9. Autocorrelation function (a) and Power spectral density (b) of the whitened noise.
图 10 噪声白化后, 光学衰减17 dB (a)和20 dB (b)下探测器的光子数响应拟合
Figure 10. Gaussian fitting results of pulse signal amplitudes under optical attenuation of 17 dB (a) and 20 dB (b), respectively, for the whitened noises.
表 1 光学衰减17 dB和20 dB下探测器的能量分辨
Table 1. Energy resolution of detector under optical attenuation of 17 dB and 20 dB.
能量分辨 $ \Delta E_{{0}}{/{\rm{eV}}} $ $ \Delta E_{{1}}{/{\rm{eV}}} $ $ \Delta E_{2}{/{\rm{eV}}} $ $ \Delta E_{3}{/{\rm{eV}}} $ $ \Delta E_{4}{/{\rm{eV}}} $ 衰减17 dB
的信号0.1015 0.3526 0.4360 0.4691 0.6140 衰减20 dB
的信号0.0955 0.3200 0.4199 0.4758 — 
DownLoad: CSV
表 2 光学衰减17 dB下使用实测噪声和白噪声模型处理后探测器能量分辨对比
Table 2. Comparison of detector energy resolutions after processing with measured noise and white noise model under optical attenuation of 17 dB.
能量分辨 $ \Delta E_{{0}}{/{\rm{eV}}} $ $ \Delta E_{{1}}{/{\rm{eV}}} $ $ \Delta E_{2}{/{\rm{eV}}} $ $ \Delta E_{3}{/{\rm{eV}}} $ $ \Delta E_{4}{/{\rm{eV}}} $ $ \Delta E_{5}{/{\rm{eV}}} $ 实测噪声 0.1015 0.3526 0.4360 0.4691 0.6140 — 白噪声模型 0.1489 0.2992 0.3772 0.4382 0.4448 0.5113 提高 –31.83% +17.85% +15.59% +7.05% +38.04% —
DownLoad: CSV
表 3 光学衰减20 dB下使用实测噪声和白噪声模型处理后探测器能量分辨对比
Table 3. Comparison of detector energy resolutions after processing with measured noise and white noise model under optical attenuation of 20 dB.
能量分辨 $ \Delta E_{{0}}{/{\rm{eV}}} $ $ \Delta E_{{1}}{/{\rm{eV}}} $ $ \Delta E_{2}{/{\rm{eV}}} $ $ \Delta E_{3}{/{\rm{eV}}} $ 实测噪声 0.0955 0.3200 0.4199 0.4758 白噪声模型 0.1553 0.2650 0.3748 0.4032 提高/% –62.61 +17.19 +10.74 +15.26
DownLoad: CSV
表 4 光学衰减17 dB下实测噪声和噪声白化后处理得到的探测器能量分辨对比
Table 4. Comparison of energy resolutions for the experimental noises and the whitening ones, where the optical pulse is attenuated 17 dB.
能量分辨 $ \Delta {{E}}_{{0}}{/{\rm{eV}}} $ $ \Delta {{E}}_{{1}}{/{\rm{eV}}} $ $ \Delta {{E}}_{2}{/{\rm{eV}}} $ $ \Delta {{E}}_{3}{/{\rm{eV}}} $ $ \Delta {{E}}_{4}{/{\rm{eV}}} $ $ \Delta {{E}}_{5}{/{\rm{eV}}} $ 实测噪声 0.1015 0.3526 0.4360 0.4691 0.6140 — 噪声白化 0.1469 0.3274 0.4263 0.4897 0.5009 0.6216 提高/% –44.73 +7.15 +2.22 –4.39 +18.42 —
DownLoad: CSV
表 5 光学衰减20 dB下实测噪声和噪声白化后处理得到的探测器能量分辨对比
Table 5. Comparison of energy resolutions for the experimental noises and the whitening ones, where the optical pulse is attenuated 20 dB.
能量分辨 $ \Delta {{E}}_{{0}}{/{\rm{eV}}} $ $ \Delta {{E}}_{{1}}{/{\rm{eV}}} $ $ \Delta {{E}}_{2}{/{\rm{eV}}} $ $ \Delta {{E}}_{3}{/{\rm{eV}}} $ 实测噪声 0.0955 0.3200 0.4199 0.4758 噪声白化 0.1932 0.2855 0.39649 0.4196 提高/% –100.02 +10.78 +5.60 +11.81
DownLoad: CSV
表 6 光学衰减20 dB下原始滤波和改进噪声模型后探测器能量分辨对比(括号中是改进后相对于实测噪声处理所得到的能量分辨的提高百分比)
Table 6. Comparison of energy resolutions of the detector for the experimental noise, white noise and withened noise, respectively. The improvemence is relative to the those for the experimental noise. Here, the optical pulse is attenuated 20 dB.
能量分辨 $ \Delta {{E}}_{1}{/{\rm{eV}}} $ $ \Delta {{E}}_{{2}}{/{\rm{eV}}} $ $ \Delta {{E}}_{3}{/{\rm{eV}}} $ 实测噪声 0.3200 0.4199 0.4758 白噪声模型 0.2650
(+17.19%)0.3748
(+10.74%)0.4032
(+15.26%)噪声白化 0.2855
(+10.78%)0.39649
(+5.60%)0.4196
(+11.81%)
DownLoad: CSV
-
[1] Hiskett P A, Lita A E, Hughes R J, Rosenberg D, Miller A J, Nordholt J E, Peterson C G, Nam S 2006 New J. Phys. 8 193
Google Scholar
[2] Knill E, Laflamme R, Milburn G J 2001 Nature 409 46
Google Scholar
[3] Zwinkels J C, Ikonen E, Fox N P, Ulm G, Rastello ML 2010 Metrologia 47 R15
Google Scholar
[4] 周品嘉 2014 博士学位论文 (成都: 西南交通大学)
Zhou P J 2014 Ph. D. Dissertation (ChengDu: Southwest Jiaotong University) (in Chinese)
[5] Enss C 2005 Cryogenic Particle Detection 1 (Berlin: Springer-Verlag) pp417−452
[6] Zheng F, Xu R, Zhu G, Jin B, Kang L, Xu W, Chen J, Wu P 2016 Sci. Rep. 6 22710
Google Scholar
[7] 张青雅, 董文慧, 何根芳, 李铁夫, 刘建设, 陈炜 2014 63 200303
Google Scholar
Zhang Q Y, Dong W H, He G F, Li T F, Liu J S, Chen W 2014 Acta Phys. Sin. 63 200303
Google Scholar
[8] Day P K, Leduc H G, Mazin B A, Vayonakis A, Zmuidzinas J 2003 Nature 425 817
Google Scholar
[9] 李春光, 王佳, 吴云, 王旭, 孙亮, 董慧, 高波, 李浩, 尤立星, 林志荣, 任洁, 李婧, 张文, 贺青, 王轶文, 韦联福, 孙汉聪, 王华兵, 李劲劲, 屈继峰 2021 70 018501
Google Scholar
Li C G, Wang J, Wu Y, Wang X, Sun L, Dong H, Gao B, Li H, You L X, Lin Z R, Ren J, Li J, Zhang W, He Q, Wang Y W, Wei L F, Sun H C, Wang H B, Li J J, Qu J F 2021 Acta Phys. Sin. 70 018501
Google Scholar
[10] 周品嘉, 王轶文, 韦联福 2014 63 070701
Google Scholar
Zhou P J, Wang Y W, Wei L F 2014 Acta Phys. Sin. 63 070701
Google Scholar
[11] Lita A E, Miller A J, Nam S W 2008 Opt. Express 16 3032
Google Scholar
[12] Lolli L, Taralli E, Portesi C, Monticone E, Rajteri M 2013 Appl. Phys. Lett. 103 041107
Google Scholar
[13] Yang X Y, Li H, Zhang W J, You L X, Zhang L, L iu, X Y, Wang Z, Peng W, Xie X M, Jiang M H 2014 Opt. Express 22 16267
Google Scholar
[14] Li X, Tan J R, Zheng K M, Zhang L B, Zhang J L, He W J, Huang P W, Li H C, Zhang B, Chen Q, Ge R, Guo S Y, Huang T, Jia X Q, Zhao Q Y, Tu X C, Kang L, Chen J, Wu P H 2020 Photonics Research 8 637
Google Scholar
[15] Geng Y, Zhang W, Li P Z, Zhong J Q, Wang Z, Miao W, Ren Y, Wang J F, Yao Q J, Shi S C 2020 J. Low Temp. Phys. 199 556
Google Scholar
[16] Guo W, Liu X, Wang Y, Wei Q, Wei L F, Hubmayr J, Fowler J, Ullom J, Vale L, Vissers M R, Gao J 2017 Appl. Phys. Lett. 110 212601
Google Scholar
[17] Liu X, Guo W, Wang Y, Dai M, Wei L F, Dober B, McKenney C M, Hilton G C, Hubmay J, Austermann J E, Ullom J N, Gao J, Ullom J N 2017 Appl. Phys. Lett. 111 252601
Google Scholar
[18] Szymkowiak A E, Kelley R L, Moseley S H, Stahle C K 1993 J. Low Temp. Phys. 93 281
Google Scholar
[19] Lindeman M A 2000 Ph. D. Dissertation (Davis, California: University of California at Davis)
[20] Anderson B D O, Moore J B 1979 Optimal Filtering (Upper Saddle River: Prentice Hall) pp417−421
[21] Walls D F, Milburn G 2008 Quantum Optics (2nd Ed.) (Berlin: Springer-Verlag) pp46−48
[22] Irwin K D 1995 Ph. D. Dissertation (Palo Alto, California: Stanford University)
[23] Wang L L, Li J, Yang N, Li X 2019 New J. Phys. 21 043005
Google Scholar
[24] 张贤达 2013 矩阵分析与应用 (第2版) (北京: 清华大学出版社) 第502−508页
Zhang X D 2013 Matrix analysis and Application (2nd Ed.) (Beijing: Tsinghua University Press) pp502−508 (in Chinese)
[25] Alpert B K, Horansky R D, Bennett D A, Doriese W B, Fowler J W, Hoover A S, Rabin M W, Ullom J N 2013 Rev. Sci. Instrum. 84 056107
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4835
- PDF Downloads: 112
- Cited By: 0
