-
动态电感探测器容易频域集成, 作为一种新兴的超导探测器件在(亚)毫米及光学波段的天文探测和阵列成像中得到了初步应用. 在单像素层面, 动态电感探测器的暗噪声水平是关键指标之一. 本文详细介绍了一种适用于动态电感探测器的噪声功率谱分析方法, 可以较好地平衡噪声频谱分辨率与方差性能, 准确且高效地进行噪声谱分析. 利用此方法, 研究了两种工艺的超导铝动态电感探测器, 发现在铝膜上下两层镀氮化硅膜的样品的频率噪声约为裸铝样品的25%—50%. 基于这种双层氮化硅工艺, 进一步研究了多种几何设计的集总结构铝动态电感探测器在不同微波功率和温度下的噪声特性, 实验结果与典型的二能级系统噪声行为相符. 本文的研究为动态电感探测器的噪声谱表征提供了一种标准方法, 并为研制低噪声的超导铝动态电感探测器奠定了基础.As a newly developed pair-breaking superconducting detector, microwave kinetic inductance detectors are simple to integrate in the frequency domain and have already been used in astronomical detection and array imaging at the (sub)millimeter and optical wavelengths. For these applications, the dark noise level of kinetic inductance detector is one of the key performance indicators. Herein a noise power spectrum analysis method is introduced in detail, which can accurately and effectively analyze the noise spectrum of kinetic inductance detector in a wide frequency range. This method can well balance the noise spectrum resolution and variance performance, by taking the noise data at the resonance frequency with two sampling rates and setting the appropriate frequency resolutions for different frequency bands. This method is used to characterize and compare the noise of aluminum (Al) kinetic inductance detectors made from two different micromachining processes. We deposite a 25-nm-thick aluminum film on high-resistivity silicon substrate for one device, while place one silicon nitride (SiNx) film on the top and one on the bottom of the aluminum film for another device. It is found that the frequency noise of the device with two silicon nitride films is about 25% to 50% of the bare aluminum device. Using this double silicon nitride film fabrication technique, we further fabricate a few groups of lumped-element aluminum kinetic inductance detectors with various inductor and interdigitated capacitor designs. We investigate the noise properties of these devices at different microwave driven power and bath temperatures, and the experimental results show typical two-level system noise behaviors. Our work provides a standard method to characterize the noise power spectrum of kinetic inductor detector, and also paves the way to developing low-noise aluminum kinetic inductance detectors for terahertz imaging, photon-counting and energy-resolving applications.
[1] Day P K, LeDuc H G, Mazin B A, Vayonakis A, Zmuidzinas J 2003 Nature 425 817
Google Scholar
[2] Zmuidzinas J 2012 Annu. Rev. Condens. Matter Phys. 3 169
Google Scholar
[3] Liu X, Guo W, Wang Y, et al. 2017 Appl. Phys. Lett. 111 252601
Google Scholar
[4] Guo W, Liu X, Wang Y, et al. 2017 Appl. Phys. Lett. 110 212601
Google Scholar
[5] De Visser P J, De Rooij S A, Murugesan V, Thoen D J, Baselmans J J 2021 Phys. Rev. Appl. 16 034051
Google Scholar
[6] Zobrist N, Clay W H, Coiffard G, Daal M, Swimmer N, Day P, Mazin B A 2022 Phys. Rev. Lett. 129 017701
Google Scholar
[7] Perotto L, Ponthieu N, Macías-Pérez J F, et al. 2020 Astron. Astrophys. 637 A71
Google Scholar
[8] Hailey-Dunsheath S, Janssen R M J, Glenn J, et al. 2021 J. Astron. Telesc. Inst. 7 011015
Google Scholar
[9] Galitzki N, Ade P, Angilè F E, et al. 2016 Millimeter, Submillimeter, and Far-Infrared Detectors and Instru- mentation for Astronomy VIII (Edinburgh: SPIE) p99140J
[10] Mazin B A, Meeker S R, Strader M J, et al. 2013 Publ. Astron. Soc. Pac. 125 1348
Google Scholar
[11] Gao J, Zmuidzinas J, Mazin B A, LeDuc H G, Day P K 2007 Appl. Phys. Lett. 90 102507
Google Scholar
[12] Gao J, Daal M, Martinis J M, et al. 2008 Appl. Phys. Lett. 92 212504
Google Scholar
[13] 周品嘉, 王轶文, 韦联福 2014 63 070701
Google Scholar
Zhou P J, Wang Y W, Wei L F 2014 Acta Phys. Sin. 63 070701
Google Scholar
[14] Kumar S, Gao J, Zmuidzinas J, Mazin B A, LeDuc H G, Day P K 2008 Appl. Phys. Lett. 92 123503
Google Scholar
[15] Vissers M R, Gao J, Sandberg M, Duff S M, Wisbey D S, Irwin K D, Pappas D P 2013 Appl. Phys. Lett. 102 232603
Google Scholar
[16] Carter F W, Khaire T, Chang C, Novosad V 2019 Appl. Phys. Lett. 115 092602
Google Scholar
[17] Moshe A G, Farber E, Deutscher G 2020 Appl. Phys. Lett. 117 062601
Google Scholar
[18] Doyle S, Mauskopf P, Naylon J, Porch A, Duncombe C 2008 J. Low Temp. Phys. 151 530
Google Scholar
[19] Noroozian O, Gao J, Zmuidzinas J, LeDuc H G, Mazin B A 2009 AIP Conf. Proc. 1185 148
Google Scholar
[20] Janssen R M J, Baselmans J J A, Endo A, et al. 2013 Appl. Phys. Lett 103 203503
Google Scholar
[21] De Visser P J, Baselmans J J A, Bueno J, Llombart N, Klapwijk T M 2014 Nat. Commun. 5 3130
Google Scholar
[22] Hubmayr J, Beall J, Becker D, et al. 2015 Appl. Phys. Lett. 106 073505
Google Scholar
[23] Vissers M R, Austermann J E, Malnou M, et al. 2020 Appl. Phys. Lett. 116 032601
Google Scholar
[24] Shi Q, Li J, Zhi Q, Wang Z, Miao W, Shi S C 2022 Sci. China, Ser. G 65 239511
Google Scholar
[25] Pridham R, Mucci R 1979 Proc. IEEE 67 904
Google Scholar
[26] Welch P 1967 IEEE Trans. Audio Electroacoust. 15 70
Google Scholar
[27] Bartlett M S 1948 Nature 161 686
Google Scholar
[28] Mazin B A, Day P K, Zmuidzinas J, Leduc H G 2002 AIP Conf. Proc. 605 309
Google Scholar
[29] Guruswamy T, Goldie D J, Withington S 2014 Supercond. Sci. Technol. 27 055012
Google Scholar
[30] Barends R, Hortensius H L, Zijlstra T, et al. 2008 Appl. Phys. Lett. 92 223502
Google Scholar
[31] Dai X, Liu X, He Q, et al. 2022 Supercond. Sci. Technol. 36 015003
Google Scholar
[32] Gao J, Daal M, Vayonakis A, et al. 2008 Appl. Phys. Lett. 92 152505
Google Scholar
-
图 1 (a)实验测量线路示意图; (b)复平面上的谐振圆及噪声示意. $ Z_{{\mathrm{c}}} $是谐振圆的圆心, $ Z_{{\mathrm{r}}} $是谐振点. 红色的点代表谐振点随时间的飘移($ {\text{δ}} Z(t) $), 可正交分解为切向的频率分量和法向的幅度分量
Fig. 1. (a) Schematic diagram of the measurement circuit; (b) schematics of the resonance circle in complex plane and noise. $ Z_{{\mathrm{c}}} $ is the center of the resonance circle and $ Z_{{\mathrm{r}}} $ is the resonance point. The red points represent the resonance frequency shift with time ($ {\text{δ}} Z(t) $), which can be projected into frequency and amplitude components, with directions tangent and normal to the resonance circle respectively.
图 2 数据处理示意图. 噪声数据被分成L段, 每段数据长度为M, 相邻两段数据的重叠点数为D
Fig. 2. Schematic diagram of data processing. The data is grouped into L segments, each segment contains M data points and D overlapped points with adjacent segments.
图 3 (a)一个典型的KID噪声功率谱, 其中红点和蓝点分别代表用100 s的降采样数据和最后1 s的连续数据计算得到的2 kHz处的频率噪声; (b) 频率分辨率对噪声谱的影响
Fig. 3. (a) A typical noise spectrum for a KID. The red dot and blue dot represent the calculated frequency noise at 2 kHz from the decimated 100 s data and the last 1 s continuous data, respectively. (b) Effects of frequency resolution on noise spectrum
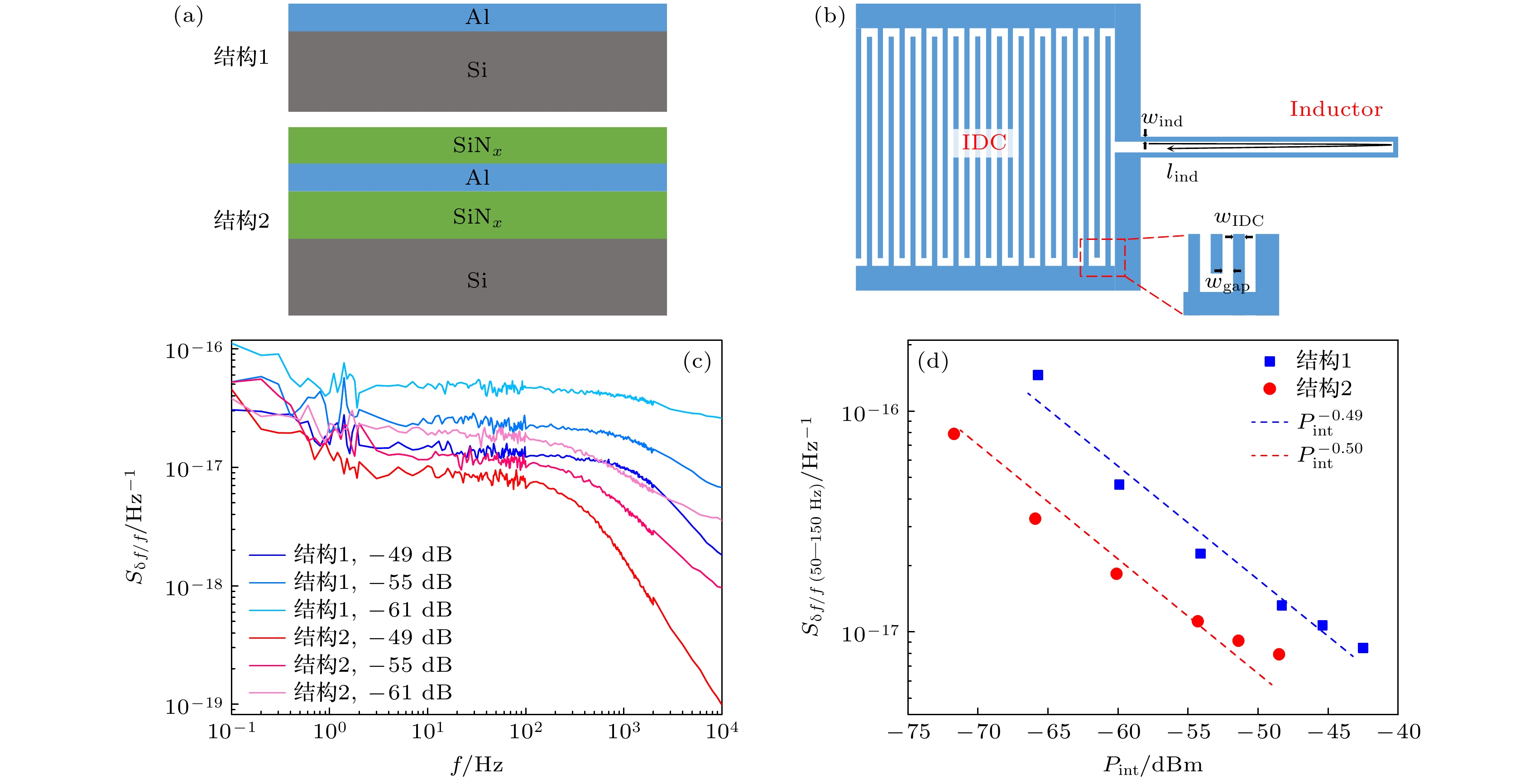
图 4 (a)两种不同的谐振器工艺结构示意图; (b)集总电路谐振器几何设计示意图; (c)两种谐振器在不同微波功率(谐振器内部功率)下的频率噪声谱; (d) 50—150 Hz的频率噪声随谐振器内部功率的变化, 可以看到双层$ {\mathrm{SiN}}_x $结构的谐振器在相同功率下具有更低的噪声
Fig. 4. (a) Schematics of two different fabrication structures for resonators; (b) geometrical design of the lumped-element resonator; (c) the measured frequency noise spectrum of two resonators with different fabrication structures at various microwave powers (the internal power of resonator); (d) the frequency noise at 50–150 Hz with resonator internal power, showing the resonator with double $ {\mathrm{SiN}}_x $ layers has a lower noise level at the same internal resonator power.
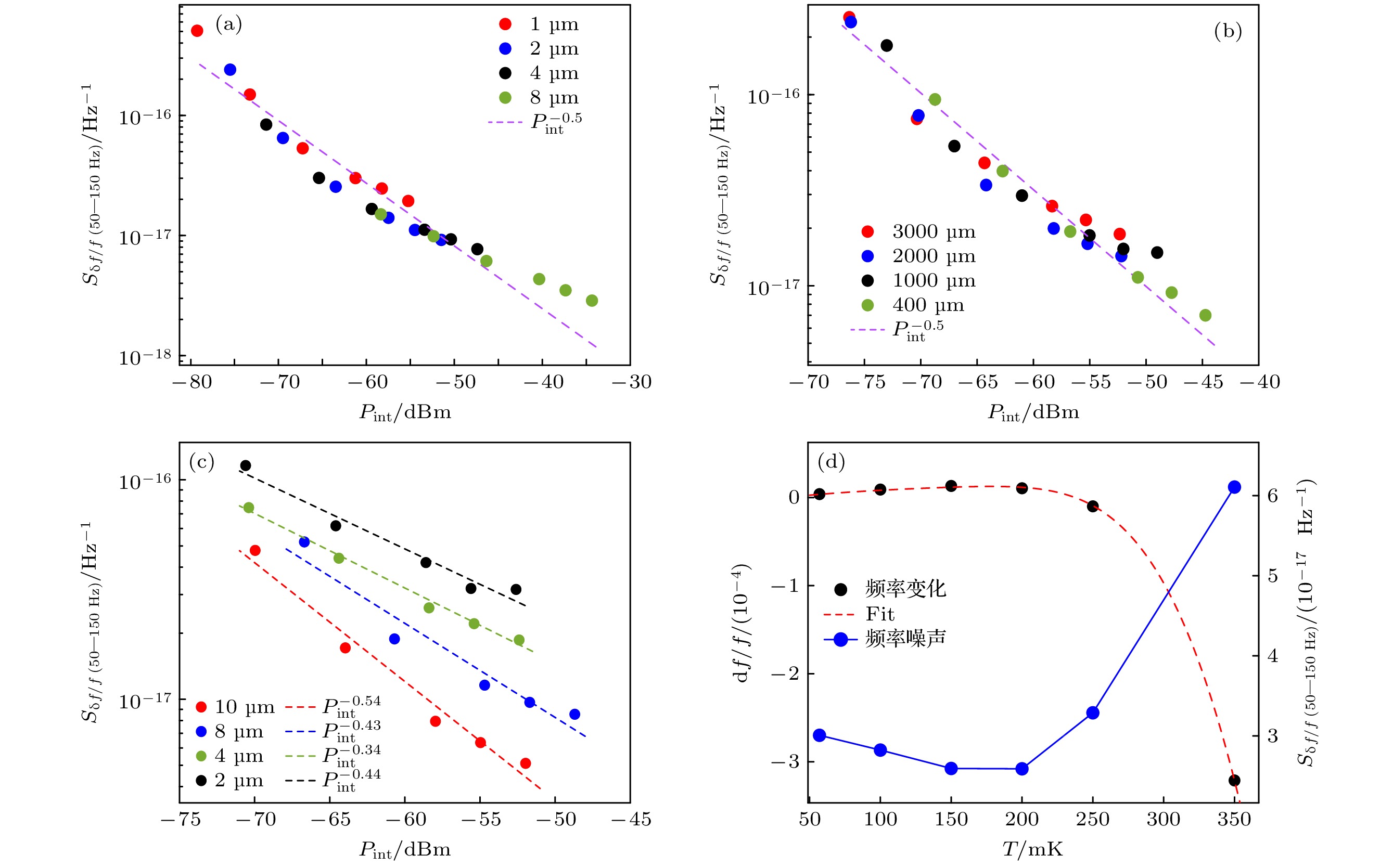
图 5 (a)不同电感条宽度谐振器的频率噪声; (b)不同电感条长度谐振器的频率噪声; (c)不同IDC手指和间隙宽度的谐振器的频率噪声; (d)谐振频率及频率噪声随温度的变化
Fig. 5. (a) Frequency noise of resonators with different inductor widths; (b) frequency noise of resonators with different inductor lengths; (c) frequency noise of resonators with different IDC finger and gap widths; (d) resonance frequency shift and frequency noise versus bath temperature.
表 1 噪声谱分析参数
Table 1. Noise spectrum analysis parameters
低频段 高频段 频率区间/Hz 0.1—2 3—100 110—2000 2000—
1.25 MHz谱分辨率$ \Delta f $/Hz 0.1 1 10 1000 分段长度M 100000 10000 1000 2500 分段数目L 19 199 1999 1999 采样频率$ F_{{\mathrm{s}}} $/Hz 10000 10000 10000 2.5 MHz 
下载: 导出CSV
表 2 两种工艺结构的谐振器测量参数
Table 2. Measured parameters of resonators with two fabrication structures
谐振器(结构) fr/GHz Qr/103 Qc/103 Qi/103 Pbif/dBm 1 0.8851 17.9 17.1 120.9 –41 2 0.8617 18.9 25.2 72.2 –48
下载: 导出CSV
-
[1] Day P K, LeDuc H G, Mazin B A, Vayonakis A, Zmuidzinas J 2003 Nature 425 817
Google Scholar
[2] Zmuidzinas J 2012 Annu. Rev. Condens. Matter Phys. 3 169
Google Scholar
[3] Liu X, Guo W, Wang Y, et al. 2017 Appl. Phys. Lett. 111 252601
Google Scholar
[4] Guo W, Liu X, Wang Y, et al. 2017 Appl. Phys. Lett. 110 212601
Google Scholar
[5] De Visser P J, De Rooij S A, Murugesan V, Thoen D J, Baselmans J J 2021 Phys. Rev. Appl. 16 034051
Google Scholar
[6] Zobrist N, Clay W H, Coiffard G, Daal M, Swimmer N, Day P, Mazin B A 2022 Phys. Rev. Lett. 129 017701
Google Scholar
[7] Perotto L, Ponthieu N, Macías-Pérez J F, et al. 2020 Astron. Astrophys. 637 A71
Google Scholar
[8] Hailey-Dunsheath S, Janssen R M J, Glenn J, et al. 2021 J. Astron. Telesc. Inst. 7 011015
Google Scholar
[9] Galitzki N, Ade P, Angilè F E, et al. 2016 Millimeter, Submillimeter, and Far-Infrared Detectors and Instru- mentation for Astronomy VIII (Edinburgh: SPIE) p99140J
[10] Mazin B A, Meeker S R, Strader M J, et al. 2013 Publ. Astron. Soc. Pac. 125 1348
Google Scholar
[11] Gao J, Zmuidzinas J, Mazin B A, LeDuc H G, Day P K 2007 Appl. Phys. Lett. 90 102507
Google Scholar
[12] Gao J, Daal M, Martinis J M, et al. 2008 Appl. Phys. Lett. 92 212504
Google Scholar
[13] 周品嘉, 王轶文, 韦联福 2014 63 070701
Google Scholar
Zhou P J, Wang Y W, Wei L F 2014 Acta Phys. Sin. 63 070701
Google Scholar
[14] Kumar S, Gao J, Zmuidzinas J, Mazin B A, LeDuc H G, Day P K 2008 Appl. Phys. Lett. 92 123503
Google Scholar
[15] Vissers M R, Gao J, Sandberg M, Duff S M, Wisbey D S, Irwin K D, Pappas D P 2013 Appl. Phys. Lett. 102 232603
Google Scholar
[16] Carter F W, Khaire T, Chang C, Novosad V 2019 Appl. Phys. Lett. 115 092602
Google Scholar
[17] Moshe A G, Farber E, Deutscher G 2020 Appl. Phys. Lett. 117 062601
Google Scholar
[18] Doyle S, Mauskopf P, Naylon J, Porch A, Duncombe C 2008 J. Low Temp. Phys. 151 530
Google Scholar
[19] Noroozian O, Gao J, Zmuidzinas J, LeDuc H G, Mazin B A 2009 AIP Conf. Proc. 1185 148
Google Scholar
[20] Janssen R M J, Baselmans J J A, Endo A, et al. 2013 Appl. Phys. Lett 103 203503
Google Scholar
[21] De Visser P J, Baselmans J J A, Bueno J, Llombart N, Klapwijk T M 2014 Nat. Commun. 5 3130
Google Scholar
[22] Hubmayr J, Beall J, Becker D, et al. 2015 Appl. Phys. Lett. 106 073505
Google Scholar
[23] Vissers M R, Austermann J E, Malnou M, et al. 2020 Appl. Phys. Lett. 116 032601
Google Scholar
[24] Shi Q, Li J, Zhi Q, Wang Z, Miao W, Shi S C 2022 Sci. China, Ser. G 65 239511
Google Scholar
[25] Pridham R, Mucci R 1979 Proc. IEEE 67 904
Google Scholar
[26] Welch P 1967 IEEE Trans. Audio Electroacoust. 15 70
Google Scholar
[27] Bartlett M S 1948 Nature 161 686
Google Scholar
[28] Mazin B A, Day P K, Zmuidzinas J, Leduc H G 2002 AIP Conf. Proc. 605 309
Google Scholar
[29] Guruswamy T, Goldie D J, Withington S 2014 Supercond. Sci. Technol. 27 055012
Google Scholar
[30] Barends R, Hortensius H L, Zijlstra T, et al. 2008 Appl. Phys. Lett. 92 223502
Google Scholar
[31] Dai X, Liu X, He Q, et al. 2022 Supercond. Sci. Technol. 36 015003
Google Scholar
[32] Gao J, Daal M, Vayonakis A, et al. 2008 Appl. Phys. Lett. 92 152505
Google Scholar
下载:
计量
- 文章访问数: 2149
- PDF下载量: 92
- 被引次数: 0
