-
Significant progress has been made in the studies of wakefield excitation in plasma by a self-modulated high energy proton beam in the past decade. The electron beams accelerated up to 2 GeV by using such a wakefield were demonstrated in the AWAKE experiment at CERN in 2018. Aiming at the application of high energy particle accelerators, new ideas have been investigated in recent years, such as seeding the proton beam self-modulation with an electron beam in order to enhance the strength and stability of the wakefield or adding a density transition in the plasma distribution to enhance the phase velocity and the strength of the wakefield. Here in this work, we investigate the effects of electron beam seeding on the phase velocity of the wakefield generated by the modulated proton beam in plasma. The physical mechanisms responsible for the phase velocity change and the roles played by the electron beam seeding are discussed. The theoretical analysis and two-dimensional particle-in-cell simulations show that both the growth rate and the phase velocity of the wakefield generated by the modulated proton beam can be enhanced by the electron beam seeding. The higher the charge density of the electron beam, the more significant the enhancement effects. The effects of electron beam energy and proton beam longitudinal profiles on the increase of phase velocity are also studied. It is shown that the evolution of the electron beam distribution has a significant effect on the seeding self-modulation process, and thus affecting the phase velocity. A self-focusing electron seeding beam can increase the phase velocity of the wakefield even to superluminal while an expanding seeding beam can reduce the phase velocity and destroy the stability of the whole process. This work may benefit the proton beam seeding self-modulation acceleration and its applications.
-
Keywords:
- plasma wakefield acceleration /
- self-modulation of proton beams /
- wakefield phase velocity /
- electron beam seeding
[1] Joshi C, Katsouleas T 2003 Phys. Today 56 47
[2] Esarey E, Sprangle P, Krall J, Ting A 1996 IEEE Trans. Plasma Sci. 24 252
Google Scholar
[3] Kudryavtsev A M, Lotov K V, Skrinsky A N 1998 Nucl. Instrum Methods A 410 388
Google Scholar
[4] Rosenzweig J, Barov N, Murokh A, Colby E, Colestock P 1998 Nucl. Instrum Methods A 410 532
Google Scholar
[5] Shiltsev V D 2012 Phys. Usp. 55 965
Google Scholar
[6] Pukhov A, Meyer-ter-Vehn J 2002 Appl. Phys. B 74 355
[7] Li W T, Wang W T, Liu J S, Wang C, Zhang Z J, Qi R, Yu C H, Li R X, Xu Z Z 2015 Chin. Phys. B 24 015205
Google Scholar
[8] Shen Z C, Min C, Zhang G B, Luo J, Weng S M, Yuan X H, Liu F, Sheng Z M 2017 Chin. Phys. B 26 115204
Google Scholar
[9] 祝昕哲, 刘维媛, 陈民 2020 69 035201
Google Scholar
Zhu X Z, Liu W Y, Chen M 2020 Acta Phys. Sin. 69 035201
Google Scholar
[10] Caldwell A, Lotov K, Pukhov A, Simon F 2009 Nat. Phys. 5 363
Google Scholar
[11] Xia G, Caldwell A, Lotov K, Pukhov A, Kumar N, An W, Lu W, Mori B, Joshi C, Huang C, Muggli P, Assmann R 2010 AIP Conf. Proc. 1299 510
[12] Kumar N, Pukhov A, Lotov K 2010 Phys. Rev. Lett. 104 255003
Google Scholar
[13] Batsch F 2020 J. Phys. Conf. Ser. 1596 012006
Google Scholar
[14] Caldwell A, Adli E, Amorim L, et al. 2016 Nucl. Instrum Methods A 829 3
Google Scholar
[15] Adli E, Ahuja A, Apsimon O, et al. 2018 Nature 561 363
Google Scholar
[16] Turner M, Adli E, Ahuja A, et al. 2019 Phys. Rev. Lett. 122 054801
Google Scholar
[17] Martorelli R, Pukhov A 2016 Phys. Plasmas 23 053109
Google Scholar
[18] Siemon C, Khudik V, Austin Yi S, et al. 2013 Phys. Plasmas 20 103111
Google Scholar
[19] Schroeder C B, Benedetti C, Esarey E, et al. 2011 Phys. Rev. Lett. 107 145002
Google Scholar
[20] Pukhov A, Kumar N, Tückmantel T, et al. 2011 Phys. Rev. Lett. 107 145003
Google Scholar
[21] Schroeder C B, Benedetti C, Esarey E, et al. 2012 Phys. Rev. E 86 026402
Google Scholar
[22] Muggli P, Morales Guzman P I, Bachmann A M, Hüther M, Moreira M, Turner M, Vieira J 2020 J. Phys. Conf. Ser. 1596 012066
Google Scholar
[23] Lotov K V, Minakov V A 2020 Plasma Phys. Controlled Fusion 62 115025
Google Scholar
[24] Lotov K V 2003 Phys. Rev. Spec. Top. Accel. Beams 6 061301
Google Scholar
[25] Li Y 2020 Studies of Proton Driven Plasma Wakefield Acceleration (Springer Nature Press) pp43−47.
[26] Lotov K V 2013 Phys. Plasmas 20 083119
Google Scholar
-
图 1 在
$ \xi =100 c/{\omega }_{\mathrm{p}} $ 处尾波相速度随时间变化 (a) 电子束密度较低时; (b) 电子束密度较大时Figure 1. Change of the phase velocity with time at
$ \xi =100 c/{\omega }_{\mathrm{p}} $ : (a) Low electron beam density; (b) high electron density.
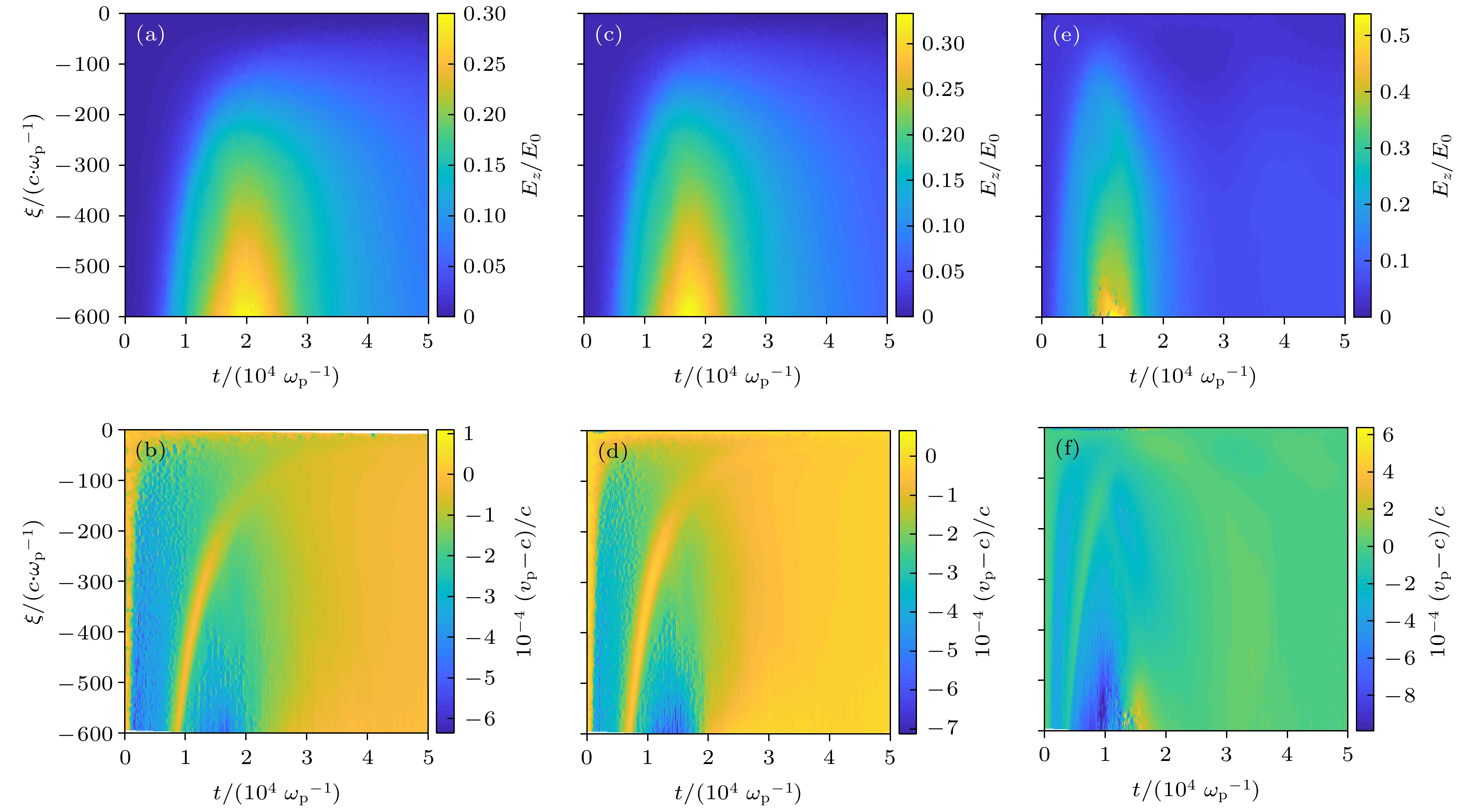
图 2 电子束种子自调制模拟结果 (a) 无电子束时的最大电场分布; (b) 无电子束时的相速度分布; (c) 电子束中心密度为
$ 1{n}_{\mathrm{b}} $ 时的最大电场分布; (b) 电子束中心密度为$ 1{n}_{\mathrm{b}} $ 时的相速度分布; (e) 电子束中心密度为$ 10{n}_{\mathrm{b}} $ 时的最大电场分布; (f) 电子束中心密度为$ 10{n}_{\mathrm{b}} $ 时的相速度分布Figure 2. Results of the simulation: (a) Distribution of Emax when no seeding; (b) distribution of phase velocity when no seeding; (c) distribution of Emax when
$ {n}_{\mathrm{b}\mathrm{e}}=1{n}_{\mathrm{b}} $ ; (d) distribution of phase velocity when$ {n}_{\mathrm{b}\mathrm{e}}=1{n}_{\mathrm{b}} $ ; (e) distribution of Emax when$ {n}_{\mathrm{b}\mathrm{e}}=10{n}_{\mathrm{b}} $ ; (f) distribution of phase velocity when$ {n}_{\mathrm{b}\mathrm{e}}=10{n}_{\mathrm{b}} $ .
图 3 (a) 不同电子束密度
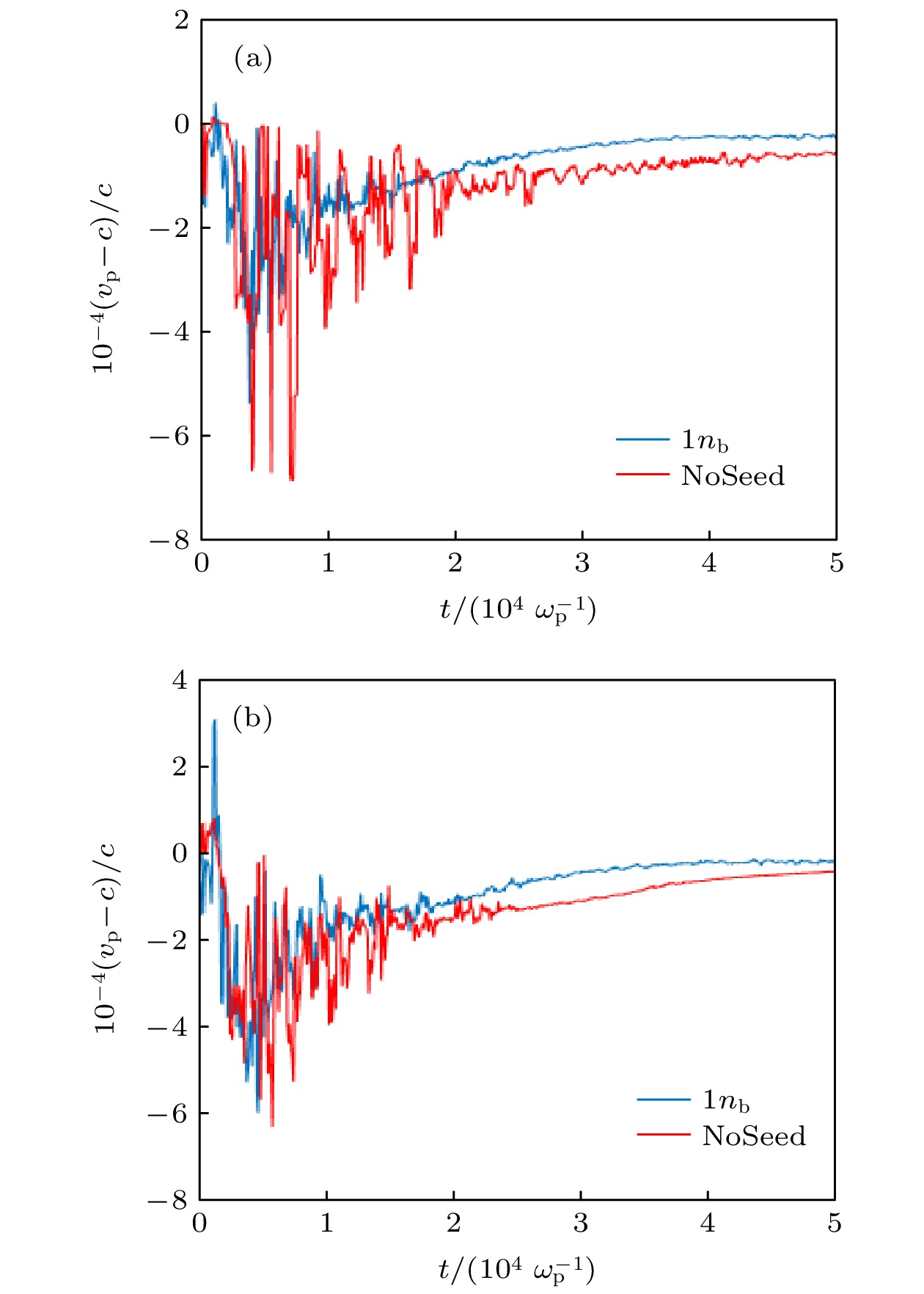
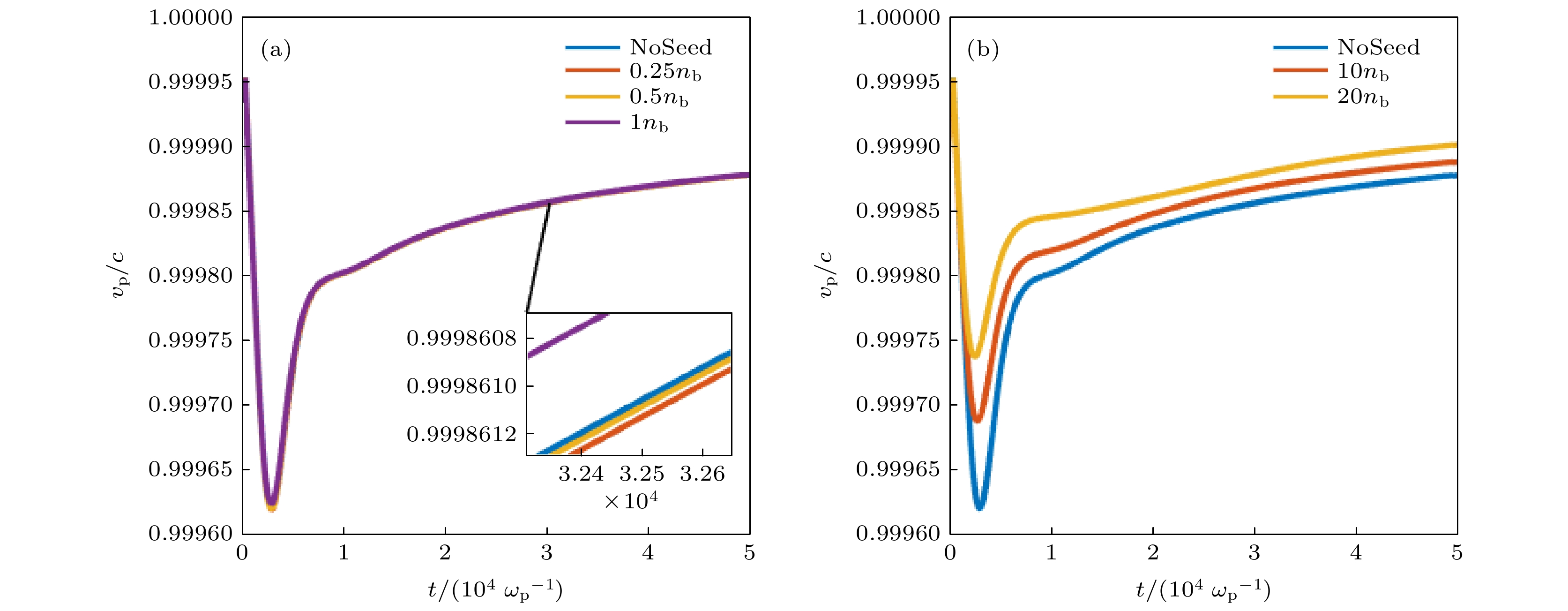
$ {n}_{\mathrm{b}\mathrm{e}} $ 情况下尾波峰值相位的变化; (b)$ \xi =100\; c/{\omega }_{\mathrm{p}} $ 处不同$ {n}_{\mathrm{b}\mathrm{e}} $ 条件下模拟得到的尾波相速度随时间变化; (c)$ \xi =300\; c/{\omega }_{\mathrm{p}} $ 处不同$ {n}_{\mathrm{b}\mathrm{e}} $ 条件下模拟得到的尾波相速度随时间变化Figure 3. (a) Phase change of the wakefield peak with different electron beam density
$ {n}_{\mathrm{b}\mathrm{e}} $ ; (b) evolution of the phase velocity at$ \xi =100 c/{\omega }_{\mathrm{p}} $ with different$ {n}_{\mathrm{b}\mathrm{e}} $ ; (c) evolution of the phase velocity at$ \xi =300 c/{\omega }_{\mathrm{p}} $ with different$ {n}_{\mathrm{b}\mathrm{e}} $ .
图 4 不同电子束密度
$ {n}_{\mathrm{b}\mathrm{e}} $ 情况下最大电场随时间的分布Figure 4. Evolution of the maximum electric field with different electron beam density
$ {n}_{\mathrm{b}\mathrm{e}} $ .
图 5 (a) 电子束能量
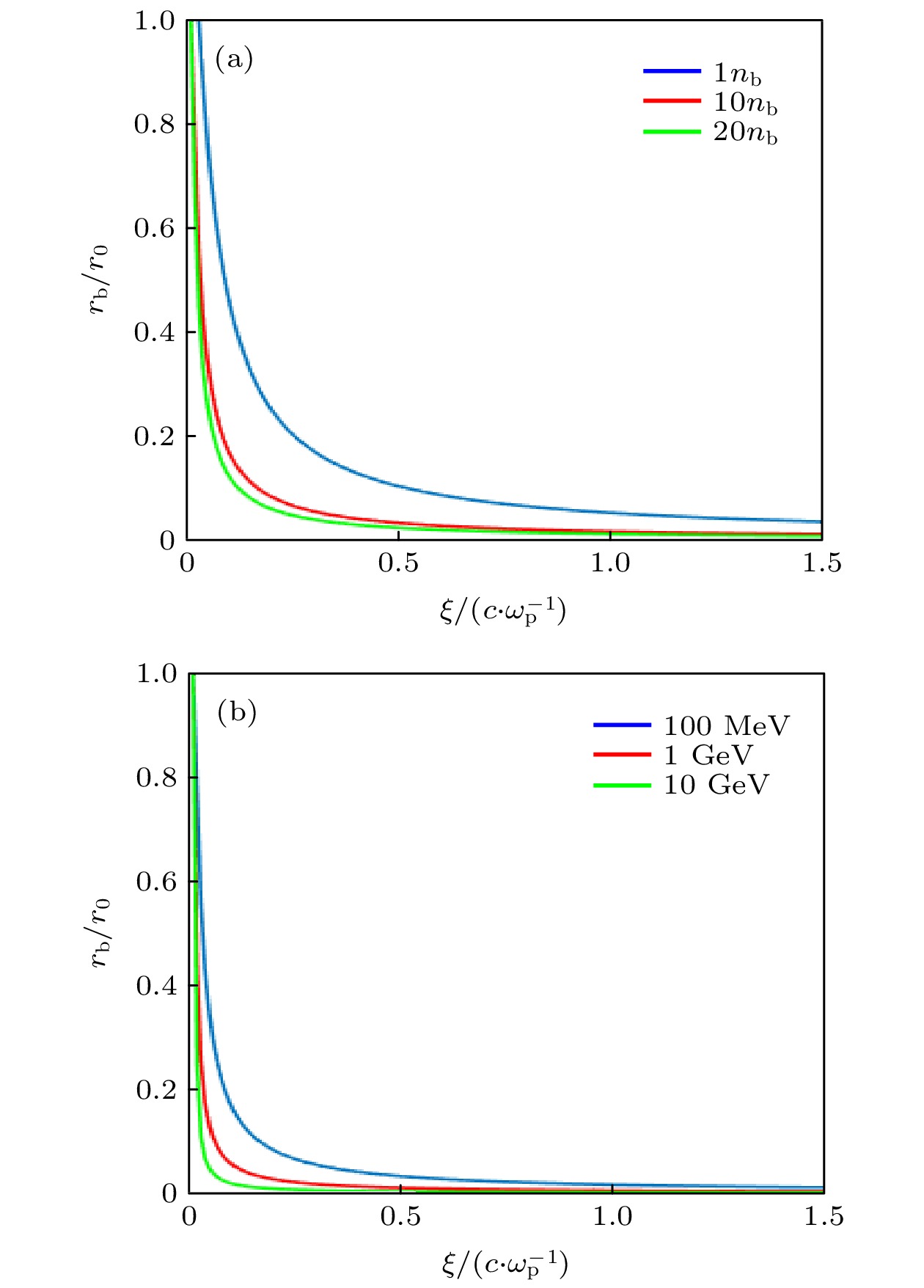
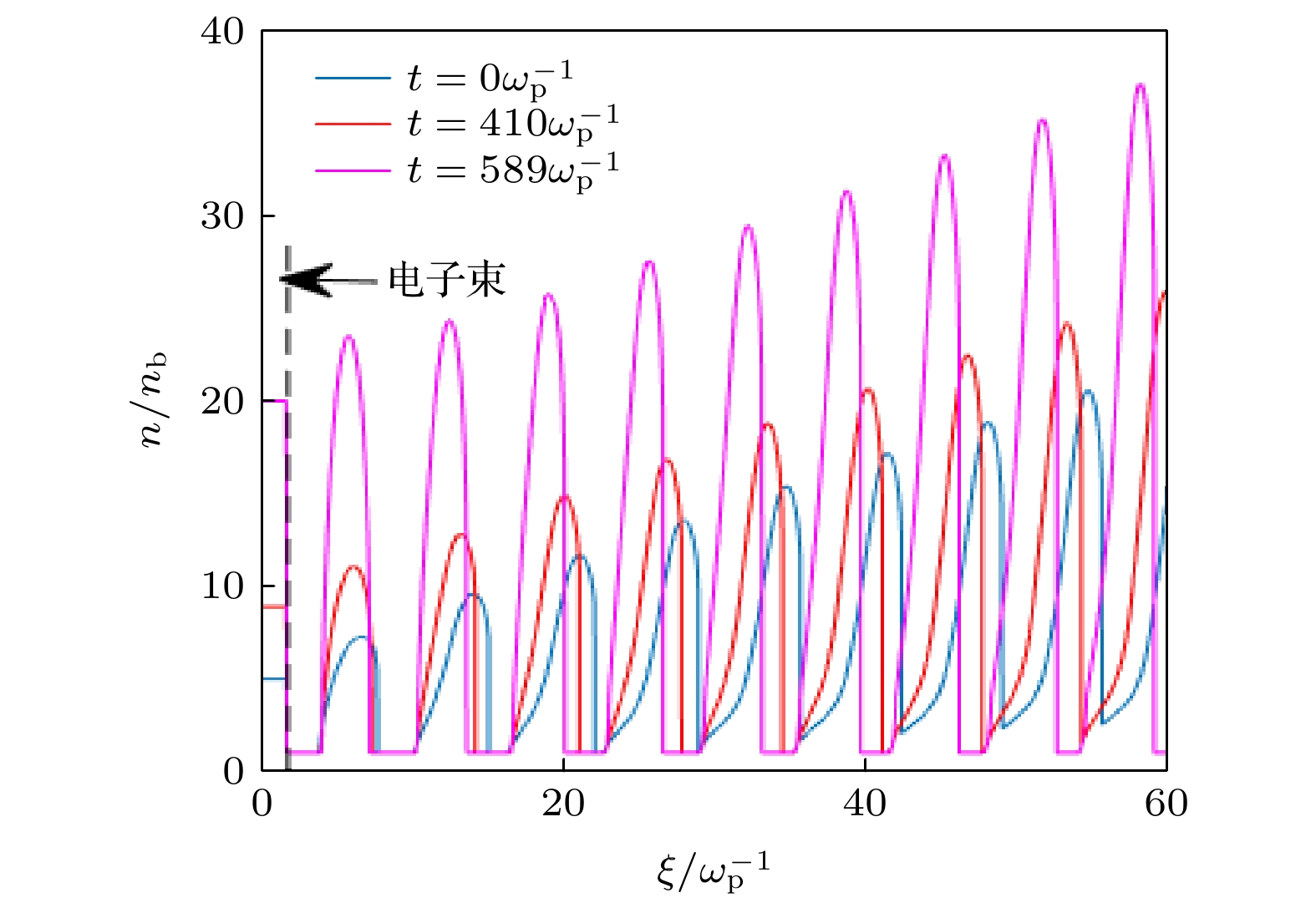
$ {E}_{\mathrm{b}\mathrm{e}}=100\mathrm{M}\mathrm{e}\mathrm{V} $ 时不同电子束密度$ {n}_{\mathrm{b}\mathrm{e}} $ 的平衡态分布; (b)$ {n}_{\mathrm{b}\mathrm{e}}=10{n}_{\mathrm{b}} $ 时不同电子束能量$ {E}_{\mathrm{b}\mathrm{e}} $ 的平衡态分布Figure 5. (a) Equilibrium configuration with different electron beam density
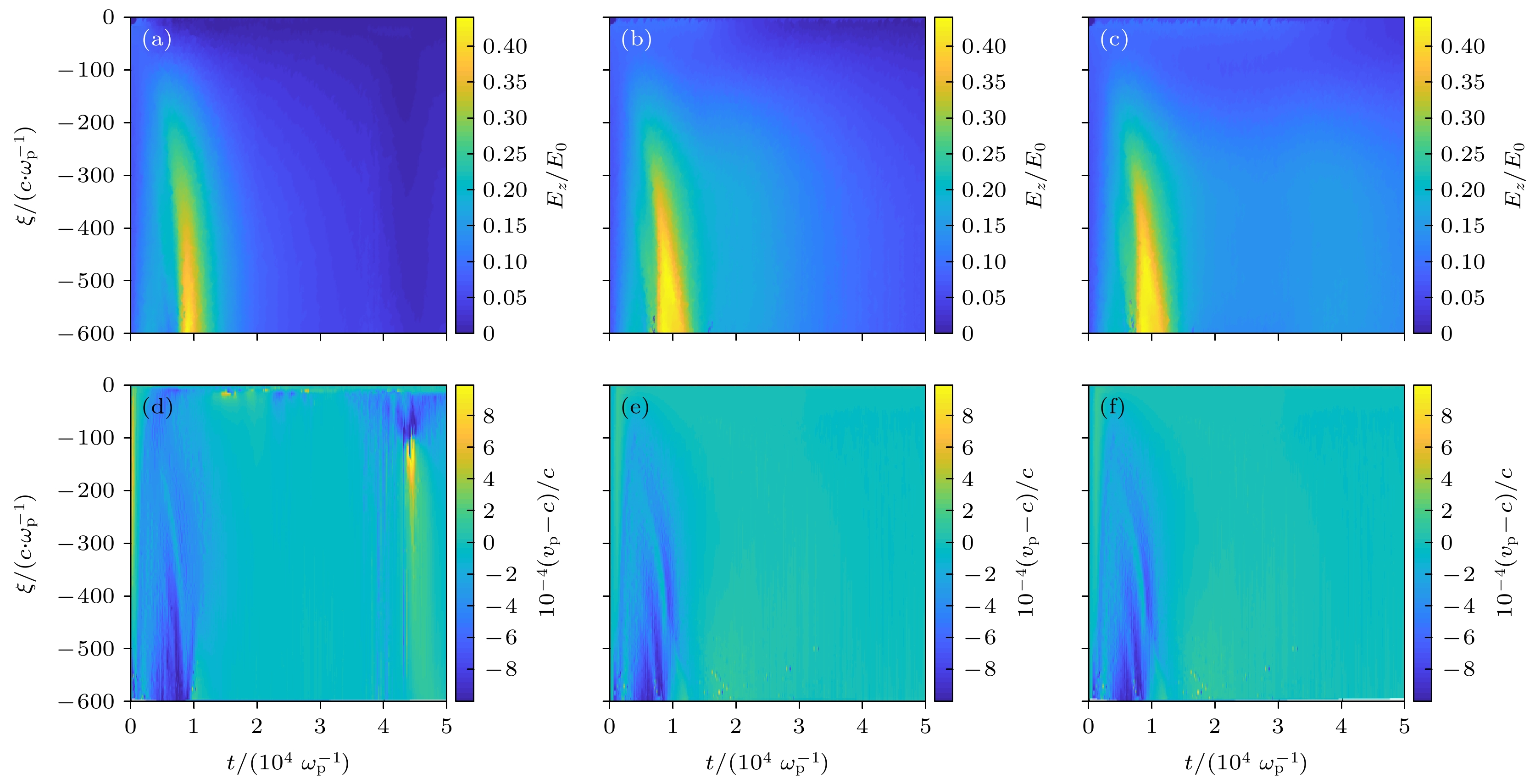
$ {n}_{\mathrm{b}\mathrm{e}} $ when Ebe =100 MeV; (b) equilibrium configuration with different E when$ {n}_{\mathrm{b}\mathrm{e}}=10{n}_{\mathrm{b}} $ .
图 6 电子束压缩引起的质子束平衡态变化, 即在三个时刻的质子束平衡态分布
Figure 6. Equilibrium configuration of proton beam with a compressing electron beam.
图 7 利用电子束种子尾波调制质子束的模拟结果 (a), (b), (c)分别对应电子束能量
$ {E}_{\mathrm{b}\mathrm{e}} $ = 100 MeV, 500 MeV, 1 GeV时的最大电场随时间变化; (d), (e), (f) 分别对应电子束能量$ {E}_{\mathrm{b}\mathrm{e}} $ = 100 MeV, 500 MeV, 1 GeV时的相速度随时间变化Figure 7. Simulation of proton beam modulation with electron beam seeding:(a), (b), (c) The maximum electric fields as a function of time for the electron beam energy at
${E}_{\mathrm{b}\mathrm{e}}=100~\mathrm{M}\mathrm{e}\mathrm{V}$ , 500 MeV, and 1 GeV, respectively; (d), (e), (f) the phase velocity as a function of time for the electron beam energy at${E}_{\mathrm{b}\mathrm{e}}=100~\mathrm{M}\mathrm{e}\mathrm{V}$ , 500 MeV, and 1 GeV, respectively.
图 8 (a) 在
$ \xi =100 c/{\omega }_{\mathrm{p}} $ 处不同电子束能量模拟得到的尾波相速度随时间变化; (b) 在$ \xi =300 c/{\omega }_{\mathrm{p}} $ 处不同电子束能量模拟得到的尾波相速度随时间变化Figure 8. (a) Phase velocity as a function of time at
$ \xi =100 c/{\omega }_{\mathrm{p}} $ for different electron energy; (b) phase velocity as a function of time at$ \xi =300 c/{\omega }_{\mathrm{p}} $ for different electron energy.
图 9 (a) 在
$ \xi =500 c/{\omega }_{\mathrm{p}} $ 处模拟得到的尾波相速度随时间变化; (b) 在$ \xi =750 c/{\omega }_{\mathrm{p}} $ 处模拟得到的尾波相速度随时间变化Figure 9. (a) Phase velocity as a function of time at
$ \xi =500 c/{\omega }_{\mathrm{p}} $ ; (b) phase velocity at$ \xi =750 c/{\omega }_{\mathrm{p}} $ . -
[1] Joshi C, Katsouleas T 2003 Phys. Today 56 47
[2] Esarey E, Sprangle P, Krall J, Ting A 1996 IEEE Trans. Plasma Sci. 24 252
Google Scholar
[3] Kudryavtsev A M, Lotov K V, Skrinsky A N 1998 Nucl. Instrum Methods A 410 388
Google Scholar
[4] Rosenzweig J, Barov N, Murokh A, Colby E, Colestock P 1998 Nucl. Instrum Methods A 410 532
Google Scholar
[5] Shiltsev V D 2012 Phys. Usp. 55 965
Google Scholar
[6] Pukhov A, Meyer-ter-Vehn J 2002 Appl. Phys. B 74 355
[7] Li W T, Wang W T, Liu J S, Wang C, Zhang Z J, Qi R, Yu C H, Li R X, Xu Z Z 2015 Chin. Phys. B 24 015205
Google Scholar
[8] Shen Z C, Min C, Zhang G B, Luo J, Weng S M, Yuan X H, Liu F, Sheng Z M 2017 Chin. Phys. B 26 115204
Google Scholar
[9] 祝昕哲, 刘维媛, 陈民 2020 69 035201
Google Scholar
Zhu X Z, Liu W Y, Chen M 2020 Acta Phys. Sin. 69 035201
Google Scholar
[10] Caldwell A, Lotov K, Pukhov A, Simon F 2009 Nat. Phys. 5 363
Google Scholar
[11] Xia G, Caldwell A, Lotov K, Pukhov A, Kumar N, An W, Lu W, Mori B, Joshi C, Huang C, Muggli P, Assmann R 2010 AIP Conf. Proc. 1299 510
[12] Kumar N, Pukhov A, Lotov K 2010 Phys. Rev. Lett. 104 255003
Google Scholar
[13] Batsch F 2020 J. Phys. Conf. Ser. 1596 012006
Google Scholar
[14] Caldwell A, Adli E, Amorim L, et al. 2016 Nucl. Instrum Methods A 829 3
Google Scholar
[15] Adli E, Ahuja A, Apsimon O, et al. 2018 Nature 561 363
Google Scholar
[16] Turner M, Adli E, Ahuja A, et al. 2019 Phys. Rev. Lett. 122 054801
Google Scholar
[17] Martorelli R, Pukhov A 2016 Phys. Plasmas 23 053109
Google Scholar
[18] Siemon C, Khudik V, Austin Yi S, et al. 2013 Phys. Plasmas 20 103111
Google Scholar
[19] Schroeder C B, Benedetti C, Esarey E, et al. 2011 Phys. Rev. Lett. 107 145002
Google Scholar
[20] Pukhov A, Kumar N, Tückmantel T, et al. 2011 Phys. Rev. Lett. 107 145003
Google Scholar
[21] Schroeder C B, Benedetti C, Esarey E, et al. 2012 Phys. Rev. E 86 026402
Google Scholar
[22] Muggli P, Morales Guzman P I, Bachmann A M, Hüther M, Moreira M, Turner M, Vieira J 2020 J. Phys. Conf. Ser. 1596 012066
Google Scholar
[23] Lotov K V, Minakov V A 2020 Plasma Phys. Controlled Fusion 62 115025
Google Scholar
[24] Lotov K V 2003 Phys. Rev. Spec. Top. Accel. Beams 6 061301
Google Scholar
[25] Li Y 2020 Studies of Proton Driven Plasma Wakefield Acceleration (Springer Nature Press) pp43−47.
[26] Lotov K V 2013 Phys. Plasmas 20 083119
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4062
- PDF Downloads: 62
- Cited By: 0
