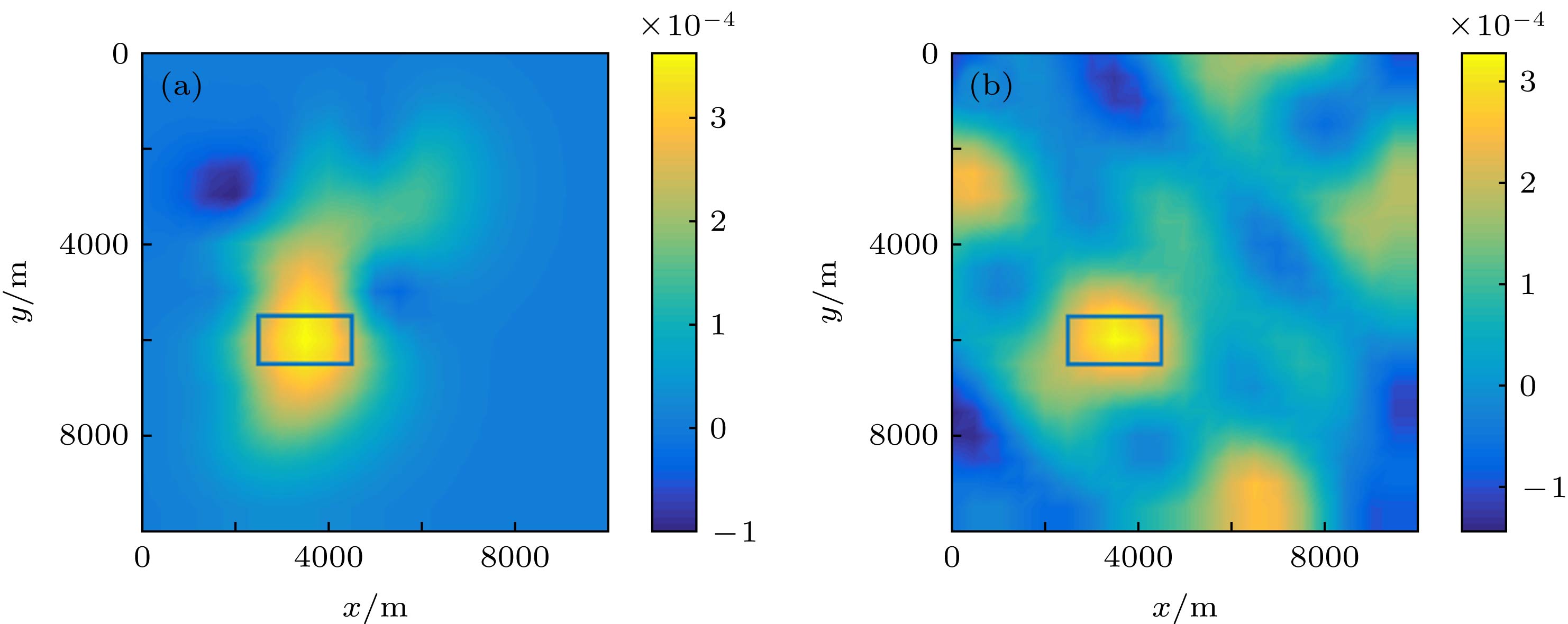
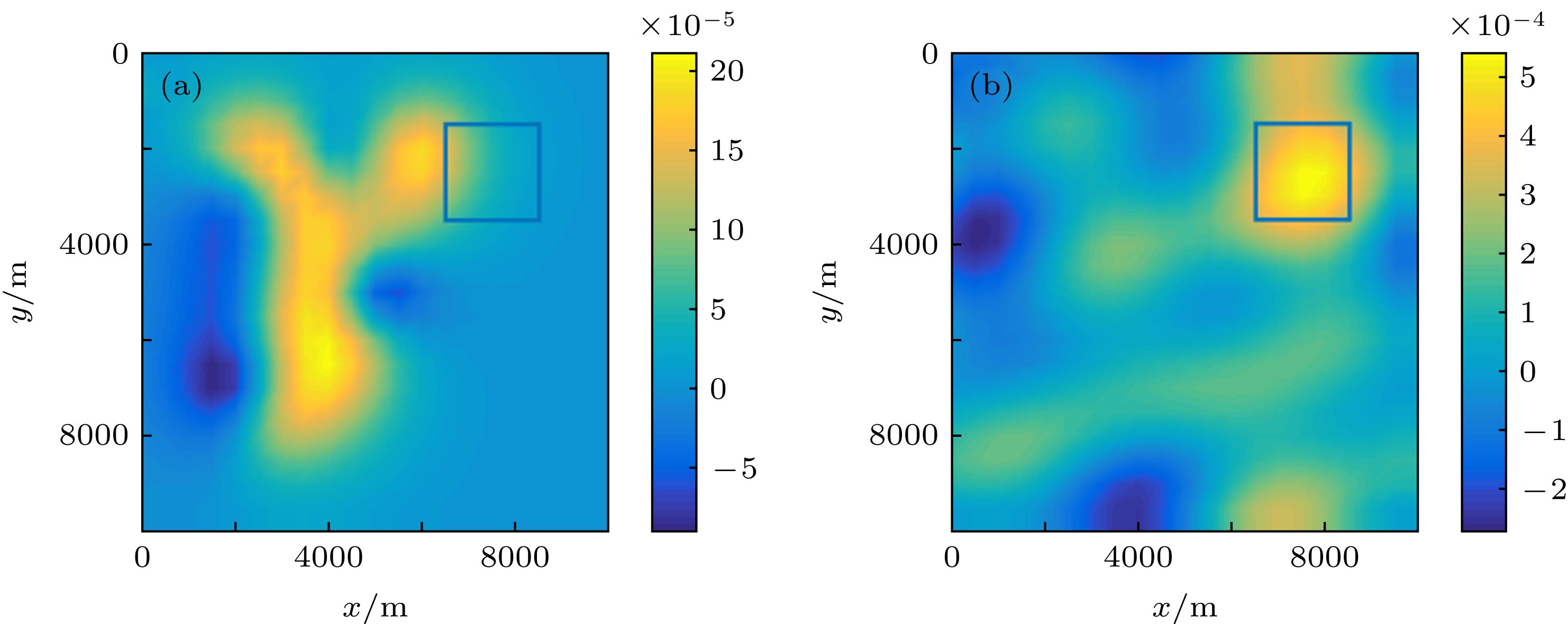
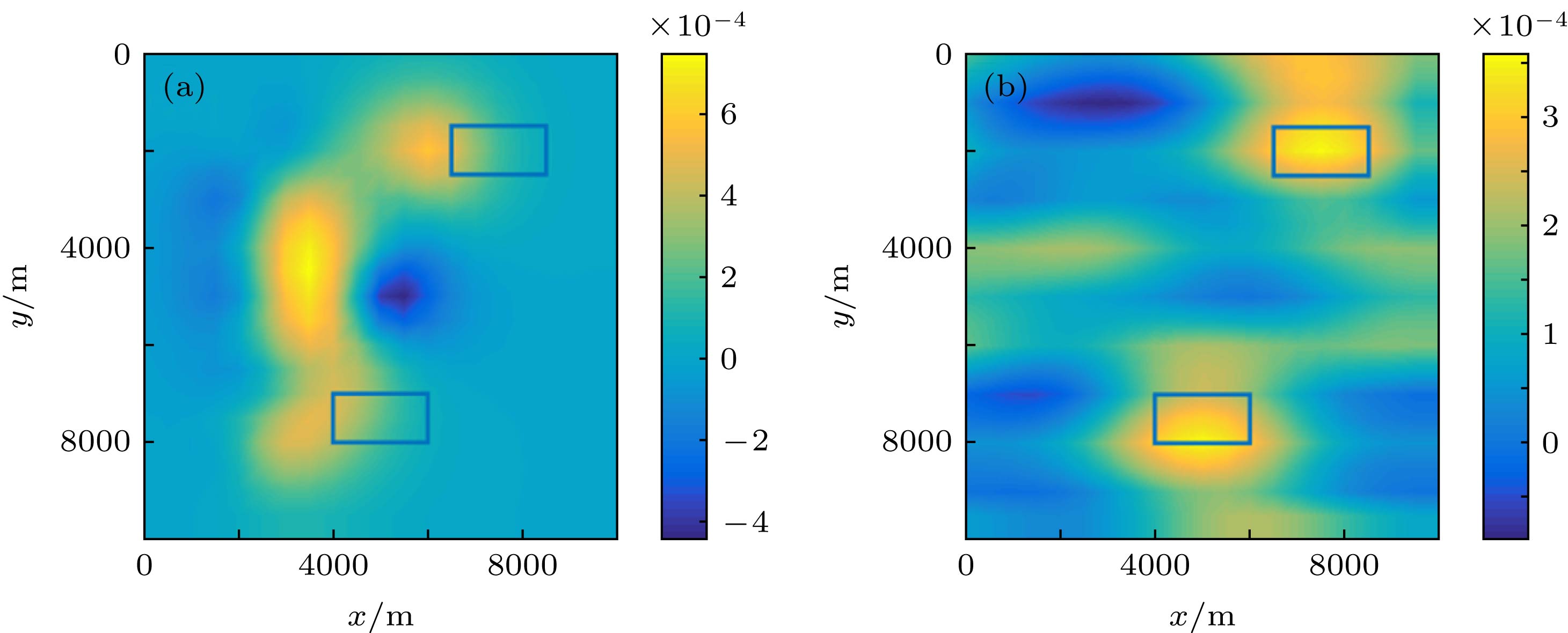
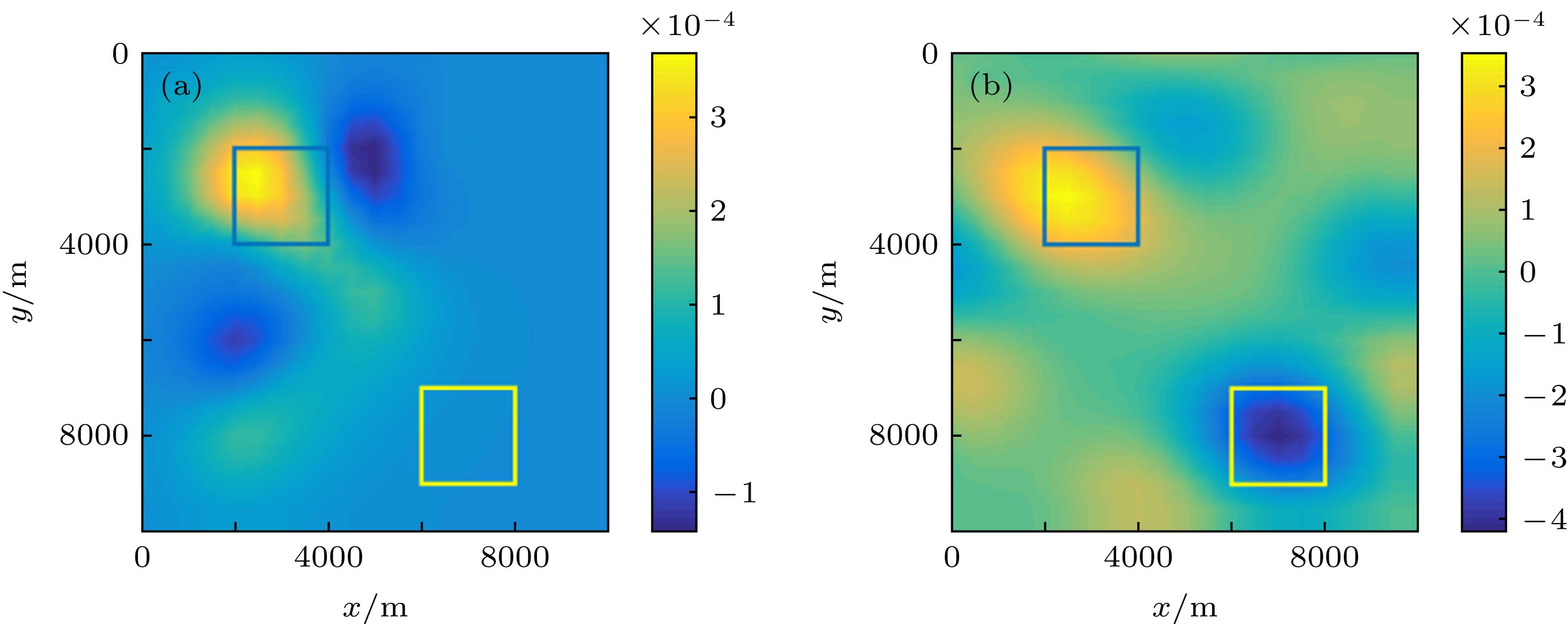
-
The coda wave interferometry is widely used in the fields of geophysics and material science. As an extension of coda wave interferometry, imaging through coda wave interferometry is a technique to obtain the spatial distribution of small velocity perturbations within a scattering medium by using time lapse and sensitivity kernels in the diffusion approximation. However, imaging through coda wave interferometry is essentially an undetermined problem without definite solution, resulting in some difficulties in accurately locating small velocity perturbations within a scattering medium. Meanwhile, compressed sensing has been used in many physical imaging systems in recent years. In this paper, we present an imaging method through coda wave interferometry to solve aforementioned problems by using sparse reconstruction algorithm which is involved in compressed sensing theory. The sparsity of velocity perturbation in its space distribution is taken into account in the proposed method. Firstly, the undetermined equation for inversion imaging is established based on the time-lapse data obtained by coda wave interferometry and the sensitivity kernel matrix in the diffusion approximation. Secondly, the inversion equation is reconstructed by using the sparse transformation within the framework of compressed sensing theory. Finally, the minimization of l1 norm is solved by the compressed sensing reconstruction algorithm, and the imaginary part for the spatial distribution of velocity perturbations is subsequently obtained. This method can accurately capture the spatial locations and ranges of both single velocity perturbation and multiple velocity perturbations in scattering medium with high computational efficiency. The numerical simulations are compared with the results from the existing linear least squares method, demonstrating that the proposed method can avoid the complex parameter determination operation, thus greatly improving the accuracy of inversion images, and also significantly reducing the calculating time.
-
Keywords:
- imaging through coda wave interferometry /
- compressed sensing /
- sensitivity kernels /
- inverse problems
[1] Snieder R 2002 Phys. Rev. E 66 046615
Google Scholar
[2] Snieder R, Grêt A, Douma H, Scales J 2002 Science 295 2253
Google Scholar
[3] Snieder R 2006 Pure. Appl. Geophys. 163 455
Google Scholar
[4] Grêt A, Snieder R, Aster R C, Kyle P R 2005 Geophys. Res. Lett. 32 233
[5] Grêt A, Snieder R, Scales J 2006 J. Geophys. Res. 111 B03305
[6] Larose E, Hall S 2009 J. Acoust. Soc. Am. 125 1853
Google Scholar
[7] Niu F, Silver P G, Daley T M, Cheng X, Majer E L 2008 Nature 454 204
Google Scholar
[8] 宋丽莉, 葛洪魁, 郭志伟, 王小琼 2012 岩石力学与工程学报 31 713
Google Scholar
Song L L, Ge H K, Guo Z W, Wang X Q 2012 Chin. J. Rock. Mech. Eng. 31 713
Google Scholar
[9] 谢凡, 任雅琼, 王宝善 2017 地球 60 1470
Google Scholar
Xie F, Ren Y Q, Wang B S 2017 Chin. J. Geophys. 60 1470
Google Scholar
[10] Pacheco C, Snieder R 2005 J. Acoust. Soc. Am. 118 1300
Google Scholar
[11] Obermann A, Planès T, Larose E, Campillo M 2013 J. Geophys. Res. 118 6285
[12] Lesage P, Reyes G, Arámbula R 2014 J. Geophys. Res. 119 4360
Google Scholar
[13] Rossetto V, Margerin L, Planès T, Larose E 2011 J. Appl. Phys. 109 034903
Google Scholar
[14] Zhang Y, Planès T, Larose E, Obermann A, Rospars C, Moreau G 2016 J. Acoust. Soc. Am. 139 1691
Google Scholar
[15] Donoho D L 2006 IEEE Trans. Inform. Theory 52 1289
Google Scholar
[16] Candes E J, Romberg J 2006 IEEE Trans. Inform. Theory 52 489
Google Scholar
[17] 宁方立, 何碧静, 韦娟 2013 62 174212
Google Scholar
Ning F L, He B J, Wei J 2013 Acta Phys. Sin. 62 174212
Google Scholar
[18] 李龙珍, 姚旭日, 刘雪峰, 俞文凯, 翟光杰 2014 63 224201
Google Scholar
Li L Z, Yao X R, Liu X F, Yu W K, Zhai G J 2014 Acta Phys. Sin. 63 224201
Google Scholar
[19] 时洁, 杨德森, 时胜国, 胡博, 朱中锐 2016 65 024302
Google Scholar
Shi J, Yang D S, Shi S G, Hu B, Zhu Z R 2016 Acta Phys. Sin. 65 024302
Google Scholar
[20] Duarte M F, Davenport M A, Takhar D, Laska J N, Sun T, Kelly K F, Baraniuk R G 2008 IEEE Sig. Proc. Mag. 25 83
Google Scholar
[21] Lingala S G, Hu Y, Dibella E, Jacob M 2011 IEEE Trans. Med. Imaging 30 1042
Google Scholar
[22] Tropp J A, Gilbert A C 2007 IEEE Trans. Inform. Theory 53 4655
Google Scholar
[23] Mikesell T D, Malcolm A E, Yang D, Haney M M 2015 Geophys. J. Int. 202 347
Google Scholar
[24] Hadziioannou C, Larose E, Coutant O, Roux P, Campillo M 2009 J. Acoust. Soc. Am. 125 3688
Google Scholar
[25] Hansen P 1992 SIAM Rev. 34 561
Google Scholar
[26] Candes E J 2008 Comptes Rendus Mathematique 346 589
Google Scholar
[27] Chen J G http://www.paper.edu.cn/releasepaper/content/200606-478 [2006-6-28]
-
图 1 多散射介质中扰动前后波形的比较 (a) 直达波扰动前后的波形; (b)尾波扰动前后的波形
Figure 1. Comparison between typical time traces of a wave propagating in a multiple scattering medium before and after a small perturbation: (a) The first arrival waves before and after a small perturbation; (b) the coda waves before and after a small perturbation.
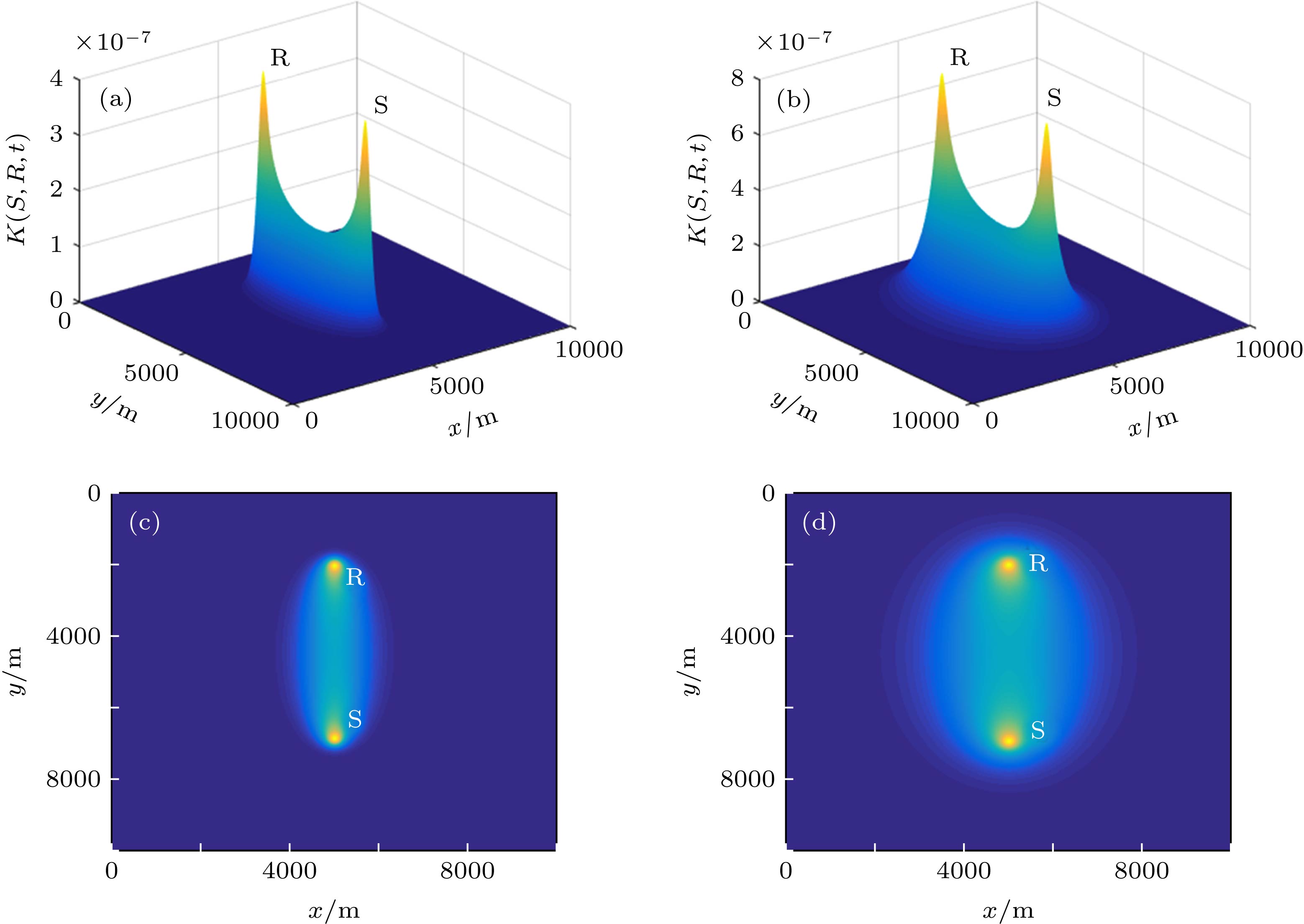
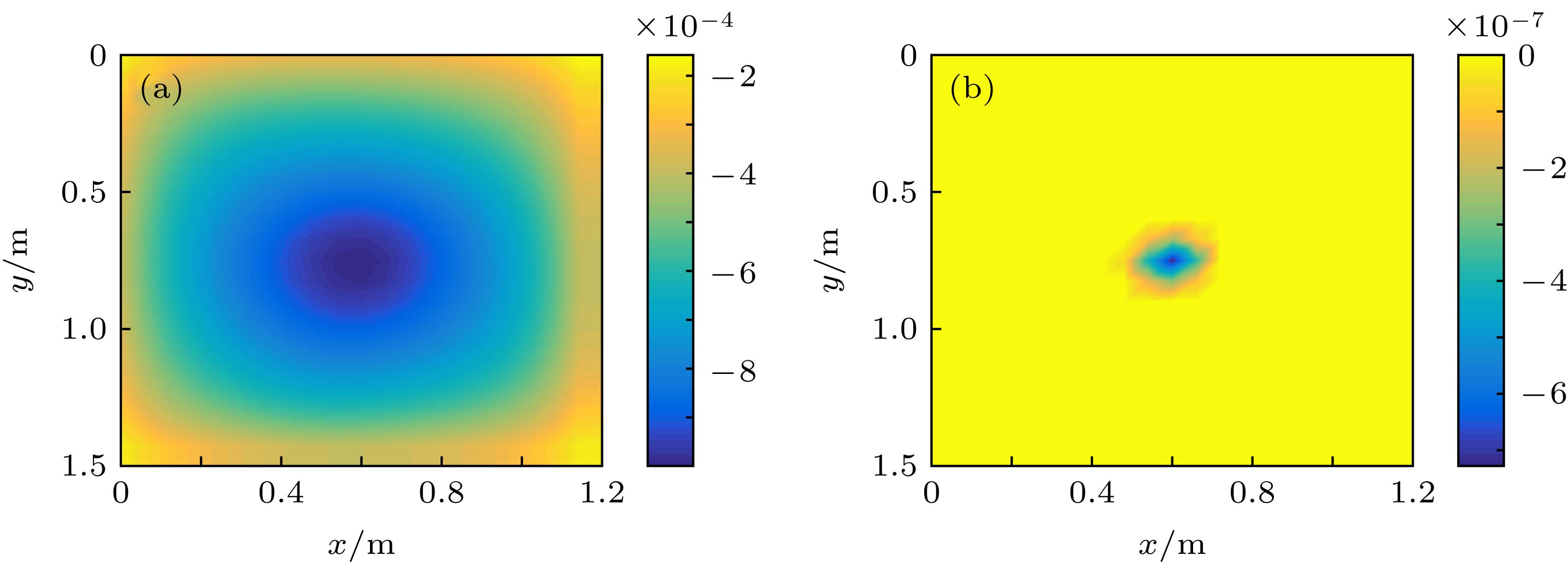
图 2 基于扩散近似的二维敏感核示例 (a) t = 1 s时的敏感核空间分布; (b) t = 5 s时的敏感核空间分布; (c) t = 1 s时的敏感核俯视图; (d) t = 5 s时的敏感核俯视图
Figure 2. Examples of sensitivity kernel based on the diffusion approximation in 2-D: (a) Spatial representation of the sensitivity kernel when t = 1 s; (b) spatial representation of the sensitivity kernel when t = 5 s; (c) vertical view of the sensitivity kernel when t = 1 s; (d) vertical view of the sensitivity kernel when t = 5 s.
图 3 二维速度场模型
Figure 3. 2-D velocity field model.
图 4 激励源及接收点布设
Figure 4. Layout of the source and receivers.
图 5 算例1 (a) 线性最小二乘法的反演图像; (b) 本文方法的反演图像
Figure 5. Case 1: (a) Inversion image of linear least squares method; (b) inversion image of the method in this paper.
图 6 算例2 (a) 线性最小二乘法的反演图像; (b) 本文方法的反演图像
Figure 6. Case 2: (a) Inversion image of linear least squares method; (b) inversion image of the method in this paper.
图 7 实验数据处理结果 (a) 线性最小二乘法的反演图像; (b) 本文方法的反演图像
Figure 7. The results of experimental data processing: (a) Inversion image of linear least squares method; (b)inversion image of the method in this paper.
图 8 算例3 (a) 线性最小二乘法的反演图像; (b) 本文方法的反演图像
Figure 8. Case 3: (a) Inversion image of linear least squares method; (b) inversion image of the method in this paper.
图 10 算例5 (a) 线性最小二乘法的反演图像; (b) 本文方法的反演图像
Figure 10. Case 5: (a) Inversion image of linear least squares method; (b) inversion image of the method in this paper.
图 9 算例4 (a) 线性最小二乘法的反演图像; (b) 本文方法的反演图像
Figure 9. Case 4: (a) Inversion image of linear least squares method; (b) inversion image of the method in this paper.
表 1 线性最小二乘法与本文方法计算成像时间对比
Table 1. The comparison of imaging time between linear least squares method and the method in this paper.
反演成像方法 成像时间/s 算例1 算例2 算例3 算例4 算例5 线性最小二乘法 1.584850 1.793517 1.601276 1.670932 2.278217 本文方法 0.264894 0.298583 0.253511 0.268969 0.115788 
DownLoad: CSV
-
[1] Snieder R 2002 Phys. Rev. E 66 046615
Google Scholar
[2] Snieder R, Grêt A, Douma H, Scales J 2002 Science 295 2253
Google Scholar
[3] Snieder R 2006 Pure. Appl. Geophys. 163 455
Google Scholar
[4] Grêt A, Snieder R, Aster R C, Kyle P R 2005 Geophys. Res. Lett. 32 233
[5] Grêt A, Snieder R, Scales J 2006 J. Geophys. Res. 111 B03305
[6] Larose E, Hall S 2009 J. Acoust. Soc. Am. 125 1853
Google Scholar
[7] Niu F, Silver P G, Daley T M, Cheng X, Majer E L 2008 Nature 454 204
Google Scholar
[8] 宋丽莉, 葛洪魁, 郭志伟, 王小琼 2012 岩石力学与工程学报 31 713
Google Scholar
Song L L, Ge H K, Guo Z W, Wang X Q 2012 Chin. J. Rock. Mech. Eng. 31 713
Google Scholar
[9] 谢凡, 任雅琼, 王宝善 2017 地球 60 1470
Google Scholar
Xie F, Ren Y Q, Wang B S 2017 Chin. J. Geophys. 60 1470
Google Scholar
[10] Pacheco C, Snieder R 2005 J. Acoust. Soc. Am. 118 1300
Google Scholar
[11] Obermann A, Planès T, Larose E, Campillo M 2013 J. Geophys. Res. 118 6285
[12] Lesage P, Reyes G, Arámbula R 2014 J. Geophys. Res. 119 4360
Google Scholar
[13] Rossetto V, Margerin L, Planès T, Larose E 2011 J. Appl. Phys. 109 034903
Google Scholar
[14] Zhang Y, Planès T, Larose E, Obermann A, Rospars C, Moreau G 2016 J. Acoust. Soc. Am. 139 1691
Google Scholar
[15] Donoho D L 2006 IEEE Trans. Inform. Theory 52 1289
Google Scholar
[16] Candes E J, Romberg J 2006 IEEE Trans. Inform. Theory 52 489
Google Scholar
[17] 宁方立, 何碧静, 韦娟 2013 62 174212
Google Scholar
Ning F L, He B J, Wei J 2013 Acta Phys. Sin. 62 174212
Google Scholar
[18] 李龙珍, 姚旭日, 刘雪峰, 俞文凯, 翟光杰 2014 63 224201
Google Scholar
Li L Z, Yao X R, Liu X F, Yu W K, Zhai G J 2014 Acta Phys. Sin. 63 224201
Google Scholar
[19] 时洁, 杨德森, 时胜国, 胡博, 朱中锐 2016 65 024302
Google Scholar
Shi J, Yang D S, Shi S G, Hu B, Zhu Z R 2016 Acta Phys. Sin. 65 024302
Google Scholar
[20] Duarte M F, Davenport M A, Takhar D, Laska J N, Sun T, Kelly K F, Baraniuk R G 2008 IEEE Sig. Proc. Mag. 25 83
Google Scholar
[21] Lingala S G, Hu Y, Dibella E, Jacob M 2011 IEEE Trans. Med. Imaging 30 1042
Google Scholar
[22] Tropp J A, Gilbert A C 2007 IEEE Trans. Inform. Theory 53 4655
Google Scholar
[23] Mikesell T D, Malcolm A E, Yang D, Haney M M 2015 Geophys. J. Int. 202 347
Google Scholar
[24] Hadziioannou C, Larose E, Coutant O, Roux P, Campillo M 2009 J. Acoust. Soc. Am. 125 3688
Google Scholar
[25] Hansen P 1992 SIAM Rev. 34 561
Google Scholar
[26] Candes E J 2008 Comptes Rendus Mathematique 346 589
Google Scholar
[27] Chen J G http://www.paper.edu.cn/releasepaper/content/200606-478 [2006-6-28]
DownLoad:
Catalog
Metrics
- Abstract views: 8251
- PDF Downloads: 84
- Cited By: 0
