-
对原子核形状共存和壳效应的研究有助于人们深入理解原子核内部结构. 物理学家们在Zn, Ge, Se, Kr的同位素研究中, 发现了显著的形状共存现象与刚性三轴性特征. 为了深入探究形状共存现象及其对原子核基态性质的影响, 我们采用相对论Hartree-Bogoliubov理论中密度依赖的介子交换模型, 对N = 32—42的偶偶核Zn, Ge, Se, Kr同位素的基态性质进行了系统研究, 获得的势能面清晰地展现了这些同位素存在形状共存和三轴性特征. 计算获得了原子核的基态能量、形变参数、双中子分离能、中子半径、质子半径和电荷半径, 结果都支持N = 40为新幻数, 部分结果也支持N = 32, 34为新幻数. 尤其, 三轴形变在其中扮演着重要角色. 进一步, 我们探讨了壳效应与形状共存现象之间可能存在的关联及其对原子核基态性质的影响, 并分析了这些变化的物理机制.
The atomic nucleus is an extremely complex quantum many- body system composed of nucleons, and its shape is determined by the number of nucleons and their interactions. The study of atomic nuclear shapes is one of the most fascinating topics in nuclear physics, providing rich insights into the microscopic details of nuclear structure. Physicists have observed significant shape coexistence phenomena and stable triaxial deformation in isotopes of Zn, Ge, Se, and Kr. This paper aims to delve deeper into the influences of shape coexistence and triaxiality on the ground-state properties of atomic nuclei, as well as to verify new magic numbers. We employ the density-dependent meson-exchange model within the framework of the relativistic Hartree-Bogoliubov (RHB) theory to systematically study the ground-state properties of even-even Zn, Ge, Se, and Kr isotopes with neutron numbers N = 32–42. The calculated potential energy surfaces clearly demonstrate the presence of shape coexistence and triaxial characteristics in theseisotopes. By analyzing the ground-state energy, deformation parameters, two-neutron separation energy, neutron radius, proton radius, and charge radius of the atomic nucleus, we discuss the closure of nuclear shells. Our results reveal that at N = 32, there is anotable abrupt change in the two-neutron separation energy values of 62Zn and 64Ge. At N = 34, a significant decrease in the two-neutron separation energy values of 68Se and 70Kr is observed, accompanied by an abrupt change in their charge radii. Meanwhile, at N = 40, clear signs of shell closure are observed. The maximum specific binding energy may be correlated with the emergence of spherical nuclear structures. The shell closure not only enhances nucleon binding energy but also suppresses nuclear deformation through symmetry constraints. Our findings support N = 40 as a new magic number, and some results also suggest that N = 32 and N = 34 can be new magic numbers. Notably, triaxial deformation plays a crucial role here. Furthermore, we explore the potential correlation between triaxiality and shape coexistence in the ground-state properties of atomic nuclei and analyze the physical mechanisms behind these changes. The discrepancies between current theoretical predictions and experimental data reflect the limitations of modeling higher-order many-body correlations (e.g. three-nucleon forces) and highlight challenges in experimental measurements for extreme nuclear regions(including neutron-rich and near-proton-drip-line regions). Future studies will combine tensor force corrections, large-scale shell model calculations, and high-precision data from next-generation radioactive beam facilities (e.g. FRIB and HIAF) to clarify the interplay among nuclear force parameterization, proton-neutron balance, and emergent symmetry, thereby providing a more comprehensive theoretical framework for studying the nuclear structures under extreme conditions. -
Keywords:
- shape coexistence /
- shell effect /
- new magic numbers
[1] Singh P, Korten W, Hagen T W, Gorgen A, Grente L, Salsac M D, Farget F, Clément E, de France G, Braunroth T, Bruyneel B, Celikovic I, Delaune O, Dewald A, Dijon A 2018 Phys. Rev. Lett. 121 192501
 Google Scholar
Google Scholar
[2] Abusara H, Ahmad S 2017 Phys. Rev. C 96 064303
[3] Cejnar P, Jolie J, Casten R F 2010 Rev. Mod. Phys. 82 2155
 Google Scholar
Google Scholar
[4] Norman E B, Drobizhev A, Gharibyan N, Gregorich K E, Kolomensky Yu G, Sammis B N, Scielzo N D, Shusterman J A, Thomas K J 2024 Phys. Rev. C 109 055501
 Google Scholar
Google Scholar
[5] Majola S N T, Shi Z, Song B Y, Li Z P, Zhang S Q, Bark R A, Sharpey-Schafer J F, Aschman D G, Bvumbi S P, Bucher T D, Cullen D M, Dinoko T S, Easton J E, Erasmus N, Greenlees P T 2019 Phys. Rev. C 100 044324
 Google Scholar
Google Scholar
[6] Yang Y L, Zhao P W, Li Z P 2023 Phys. Rev. C 107 024308
 Google Scholar
Google Scholar
[7] Hua H, Wu C Y, Cline D, Hayes A B, Teng R, Clark R M, Fallon P, Goergen A, Macchiavelli A O, Vetter K 2004 Phys. Rev. C 69 014317
 Google Scholar
Google Scholar
[8] Cwiok S, Heenen P H, Nazarewicz W 2005 Nature 433 705
 Google Scholar
Google Scholar
[9] Ayangeakaa A D, Janssens R V F, Wu C Y, Allmond J M, Wood J L, Zhu S, Albers M, Almaraz-Calderon S, Bucher B, Carpenter M P, Chiara C J, Cline D, Crawford H L, Harker J, Hayes A B, Hoffman C R, Kay B P, Kolos K, Korichi A 2016 Phys. Lett. B 754 254
 Google Scholar
Google Scholar
[10] 圣宗强, 郭建友 2008 57 1557
 Google Scholar
Google Scholar
Sheng Z Q, Guo J Y 2008 Acta Phys. Sin. 57 1557
 Google Scholar
Google Scholar
[11] 焦朋, 郭建友, 方向正 2010 59 2369
 Google Scholar
Google Scholar
Jiao P, Guo J Y, Fang X Z 2010 Acta Phys. Sin. 59 2369
 Google Scholar
Google Scholar
[12] 王刚, 方向正, 郭建友 2012 61 102101
 Google Scholar
Google Scholar
Wang G, Fang X Z, Guo J Y 2012 Acta Phys. Sin. 61 102101
 Google Scholar
Google Scholar
[13] Nomura K, Rodriguez-Guzman R, Robledo L M 2016 Phys. Rev. C 94 044314
 Google Scholar
Google Scholar
[14] Karim A, Siddiqui T A, Ahmad S 2022 Phys. At. Nucl. 85 588
 Google Scholar
Google Scholar
[15] Zhang X Y, Niu Z M, Sun W, Xia X W 2023 Phys. Rev. C 108 024310
[16] Garcia-Ramos J E, Arias J M, Dukelsky J 2014 Phys. Lett. B 736 333
 Google Scholar
Google Scholar
[17] 童红, 张春梅, 石筑一, 汪红, 倪绍勇 2010 59 3136
 Google Scholar
Google Scholar
Tong H, Zhang C, Shi Z Y, Wang H, Ni S Y 2010 Acta Phys. Sin. 59 3136
 Google Scholar
Google Scholar
[18] Bonatsos D, Assimakis I E, Minkov N, Martinou A 2017 Phys. Rev. C 95 064326
 Google Scholar
Google Scholar
[19] 支启军 2011 60 052101
 Google Scholar
Google Scholar
Zhi Q J 2011 Acta Phys. Sin. 60 052101
 Google Scholar
Google Scholar
[20] Wu X H, Ren Z X, Zhao P W 2022 Phys. Rev. C 105 L031303
[21] Gupta S, Bakshi R, Gupta S, Singh S, Bharti A, Bhat G H, Sheikh J A 2023 Eur. Phys. J. A 59 258
 Google Scholar
Google Scholar
[22] 卢希庭, 江栋兴, 叶沿林 2000 原子核物理(北京: 原子能出版社)第192页
Lu X T, Jiang D X, Ye Y L 2000 Nuclear Physics (Beijing: Atomic Energy Press) p192
[23] Wienholtz F, Beck D, Blaum K, Borgmann C, Breitenfeldt M, Cakirli R B, George S, Herfurth F, Holt J D, Kowalska M, Kreim S, Lunney D, Manea V, Menendez J, Neidherr D, Rosenbusch M, Schweikhard L, Schwenk A, Simonis J, Stanja J, Wolf R N, Zuber K 2013 Nature 498 346
 Google Scholar
Google Scholar
[24] Steppenbeck D, Takeuchi S, Aoi N, Doornenbal P, Matsushita M, Wang H, Baba H, Fukuda N, Go S, Honma M, Lee J, Matsui K, Michimasa S, Motobayashi T, Nishimura D, Otsuka T, Sakurai H, Shiga Y, Soderstrom P A, Sumikama T, Suzuki H, Taniuchi R, Utsuno Y, Valiente-Dobon J J, Yoneda K 2013 Nature 502 207
 Google Scholar
Google Scholar
[25] Michimasa S, Kobayashi M, Kiyokawa Y, Ota S, Ahn D S, Baba H, Berg G P A, Dozono M, Fukuda N, Furuno T, Ideguchi E, Inabe N, Kawabata T, Kawase S, Kisamori K, Kobayashi K, Kubo T, Kubota Y, Lee C S, Matsushita M, Miya H, Mizukami A, Nagakura H, Nishimura D, Oikawa H, Sakai H, Shimizu Y, Stolz A, Suzuki H, Takaki M, Takeda H, Takeuchi S, Tokieda H, Uesaka T, Yako K, Yamaguchi Y, Yanagisawa Y, Yokoyama R, Yoshida K, Shimoura S 2018 Phys. Rev. Lett. 121 022506
 Google Scholar
Google Scholar
[26] Liu J, Niu Y F, Long W H 2020 Phys. Lett. B 806 135524
 Google Scholar
Google Scholar
[27] Zhang W, Huang J K, Sun T T, Peng J, Zhang S Q 2024 Chin. Phys. C 48 104105
 Google Scholar
Google Scholar
[28] Ring P 1996 Prog. Part. Nucl. Phys. 37 193
 Google Scholar
Google Scholar
[29] Vretenar D, Afanasjev A V, Lalazissis G A, Ring P 2005 Phys. Rep. 409 101
 Google Scholar
Google Scholar
[30] Meng J, Toki H, Zhou S G, Zhang S Q, Long W H, Geng L S 2006 Prog. Part. Nucl. Phys. 57 470
 Google Scholar
Google Scholar
[31] Liang H Z, Meng J, Zhou S G 2015 Phys. Rep. 570 1
 Google Scholar
Google Scholar
[32] Niksic T, Paar N, Vretenar D, Ring P 2014 Comput. Phys. Commun. 185 1808
 Google Scholar
Google Scholar
[33] Ring P, Schuck P 1981 Phys. Today 36 70
[34] Staszack A, Stoitsov M, Baran A, Nazarewicz W 2010 Eur. Phys. J. A 46 85
 Google Scholar
Google Scholar
[35] Tian Y, Ma Z Y, Ring P 2009 Phys. Lett. B 676 44
 Google Scholar
Google Scholar
[36] Niksic T, Ring P, Vretenar D, Tian Y, Ma Z Y 2010 Phys. Rev. C 81 054318
 Google Scholar
Google Scholar
[37] 沈水法, 王华磊, 孟海燕, 阎玉鹏, 沈洁洁, 王飞鹏, 蒋海滨, 包莉娜 2021 70 192101
 Google Scholar
Google Scholar
Shen S F, Wang H L, Meng H Y, Yan Y P, Shen J J, Wang F P, Jiang H B, Bao L N 2021 Acta Phys. Sin. 70 192101
 Google Scholar
Google Scholar
[38] Wang M, Huang W J, Kondev F G, Audi G, Naimi S 2021 Chin. Phys. C 45 030003
 Google Scholar
Google Scholar
[39] Wang S J, Kanellakopoulos A, Yang X F, Bai S W, Billowes J, Bissell M L, Blaum K, Cheal B, Devlin C S, Garcia Ruiz R F, Han J Z, Heylen H, Kaufmann S, König K, Koszorús Á, Lechner S, Malbrunot-Ettenauer S, Nazarewicz W, Neugart R, Neyens G, Nörtershäuser W, Ratajczyk T, Reinhard P G, Rodríguez L V, Sels S, Xie L, Xu Z Y, Yordanov D T, Yu Y M 2024 Phys. Lett. B 856 138867
 Google Scholar
Google Scholar
[40] El Adri M, Oulne M 2020 Int. J. Mod. Phys. E 29 2050089
[41] 陈翠红, 李占奎, 王秀华, 李荣华, 方芳, 王柱生, 李海霞 2023 72 122902
 Google Scholar
Google Scholar
Chen C H, Li Z K, Wang X H, Li R H, Fang F, Wang Z S, Li H X 2023 Acta Phys. Sin. 72 122902
 Google Scholar
Google Scholar
[42] Liu Y, Wang R, Mushtaq Z, Tian Y , He X H, Qiu H, Chen X R 2025 Chin. Phys. C 49 034103
[43] Enciu M, Liu H N, Obertelli A, Doornenbal P, Nowacki F, Ogata K, Poves A, Yoshida K, Achouri N L 2022 Phys. Rev. Lett. 129 262501
 Google Scholar
Google Scholar
-
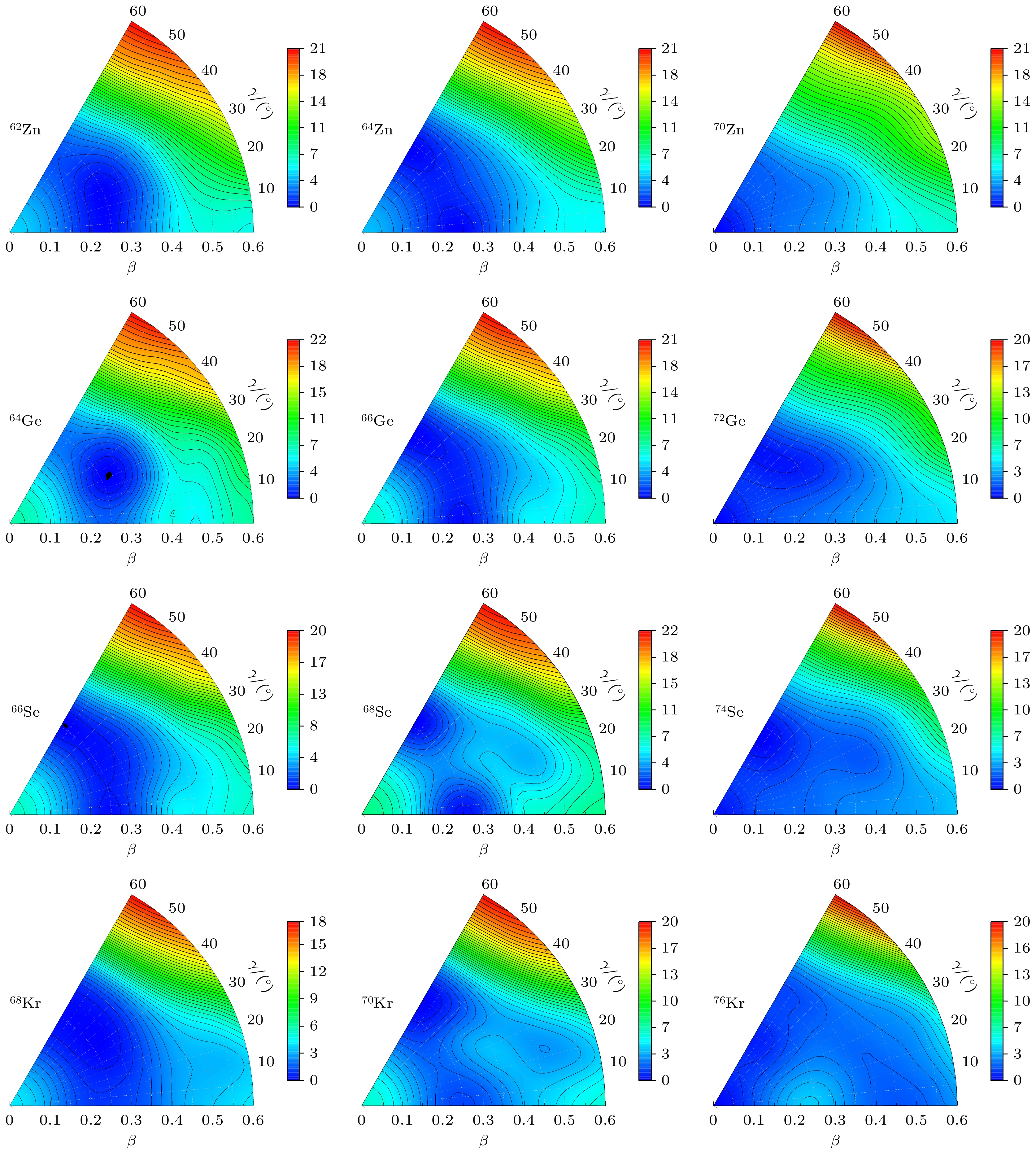
图 1 采用DD-ME2有效相互作用, 通过约束四极变形的三轴RHB计算生成中子数N = 32, N = 34, N = 40的Zn, Ge, Se, Kr同位素的势能曲面. 所有势能面经过归一化处理, 最小值代表基态能量. 等高线由能量相同点连成, 相邻等高线之间的能差为0.6 MeV
Fig. 1. The potential energy surfaces of Zn, Ge, Se, Kr isotopes, with neutron numbers N = 32, N = 34, and N = 40. These surfaces are generated through triaxial RHB calculations with constrained quadrupole deformation, employing the DD-ME2 effective interactions. The scale of the potential energy is consistent across all surfaces, and the lowest minimum represents the ground state. The contours join points on the surface with the same energy, and the separation between neighboring contours is 0.6 MeV.
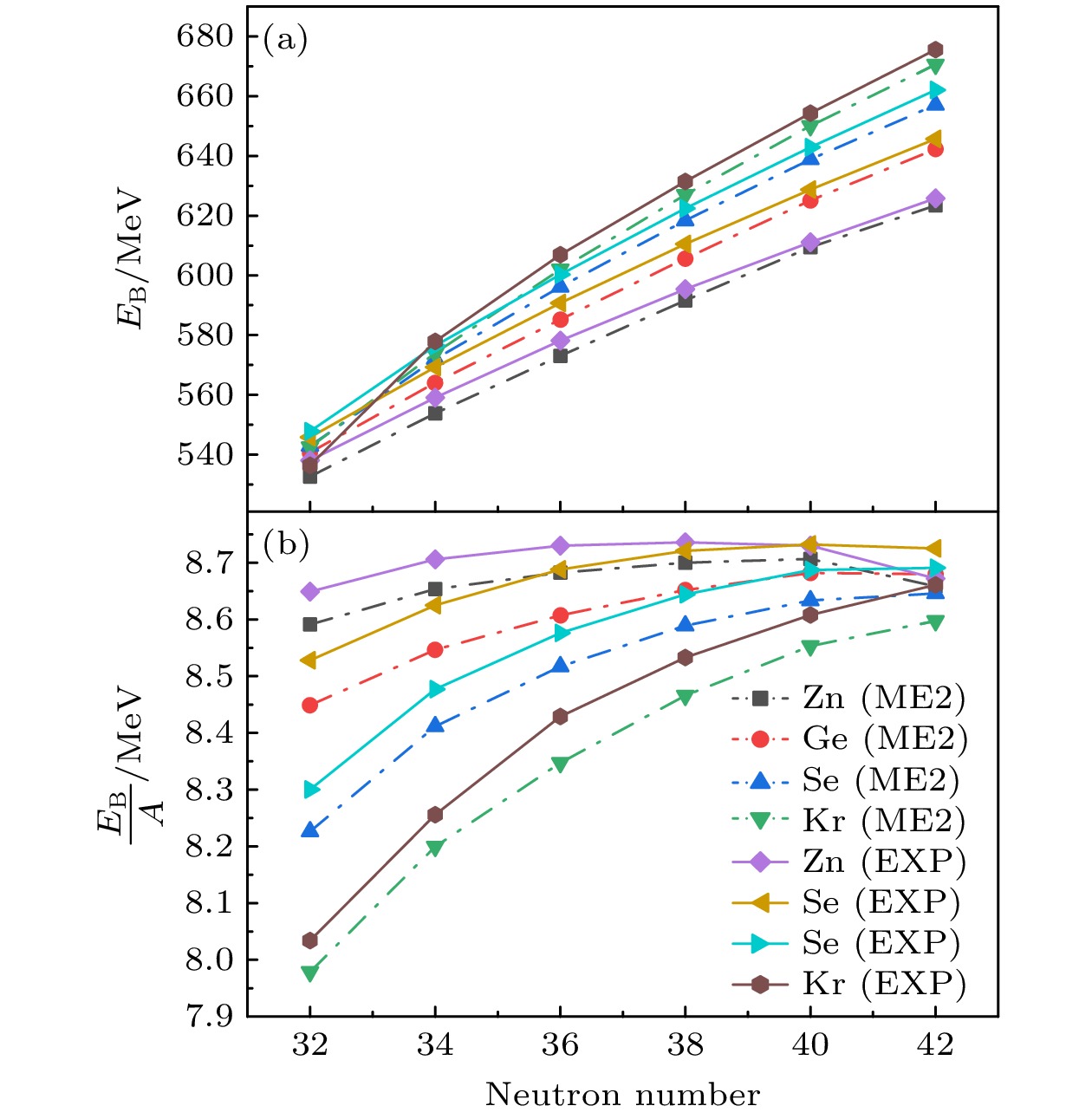
图 2 采用DD-ME2有效相互作用, 通过约束四极变形的三轴RHB计算生成中子数N = 32—42的Zn, Ge, Se, Kr偶偶核同位素的结合能与比结合能, 并与参考文献[38,39]中的实验值进行对比
Fig. 2. The binding energy per nucleon and the total binding energy of N = 32–42 Zn, Ge, Se, Kr isotopes in the triaxial RHB calculations using both the DD-ME2 interactions, with comparisons made to experimental data from Ref. [38,39].
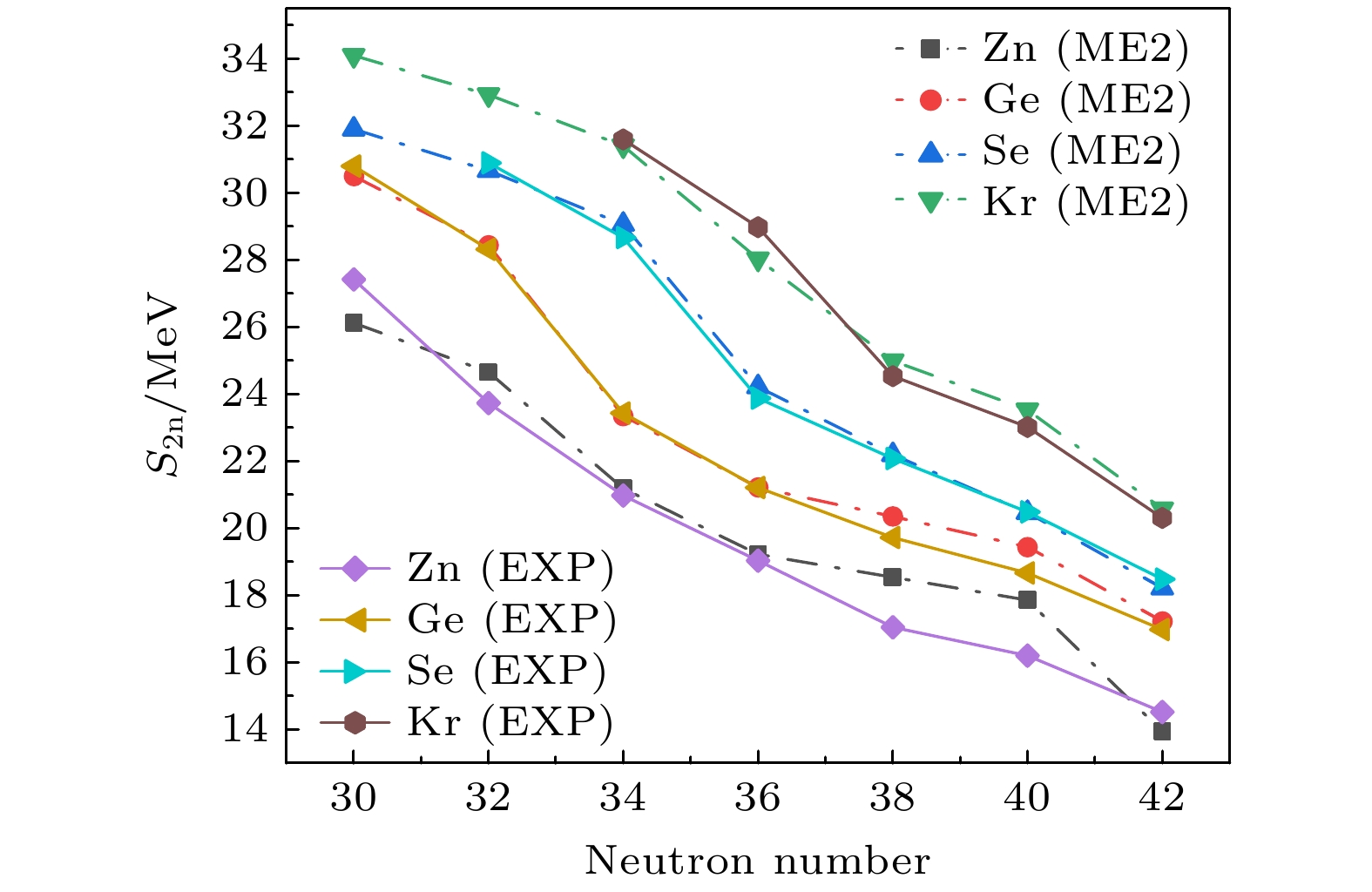
图 3 采用DD-ME2有效相互作用, 通过约束四极变形的三轴RHB计算生成中子数N = 32—42的Zn, Ge, Se, Kr偶偶核同位素的双中子分离能, 并与参考文献[38,39]中的实验值进行对比
Fig. 3. The two-neutron separation energy for N = 32–42 Zn, Ge, Se, Kr isotopes, obtained through triaxial RHB calculations using the DD-ME2 interactions, with comparisons made to experimental data from Ref. [38,39].
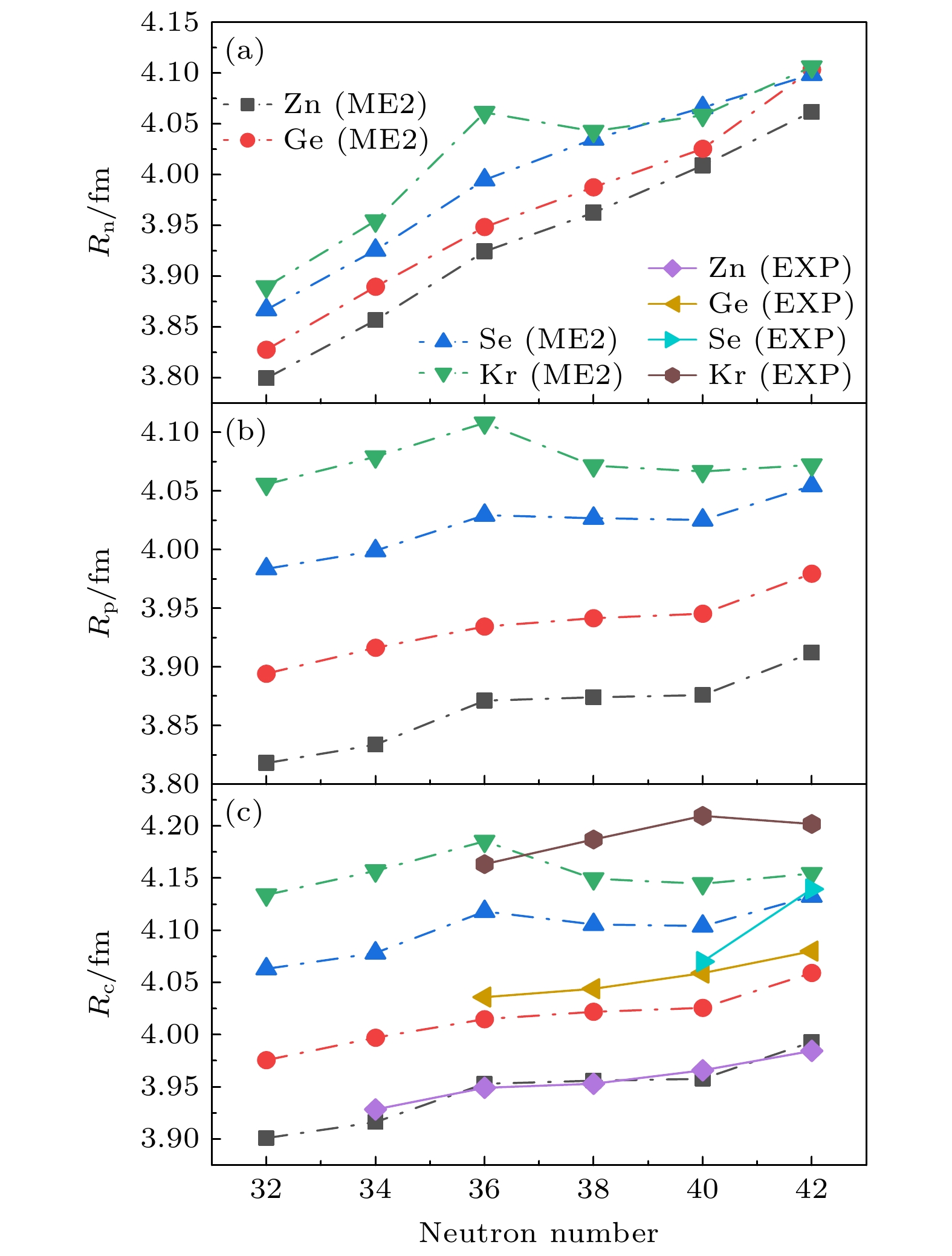
图 4 采用DD-ME2有效相互作用, 通过约束四极变形的三轴RHB计算生成中子数N = 32—42的Zn, Ge, Se, Kr偶偶核同位素的中子、质子半径与电荷半径, 并与参考文献[38,39]中电荷半径的实验值进行对比
Fig. 4. The neutron, proton, and charge radii for N = 32–42 Zn, Ge, Se, Kr isotopes in the triaxial RHB calculations using the DD-ME2 interactions, with comparisons made to charge radii experimental data from Ref. [38,39].
表 1 势能曲面极小值点, 坐标(β, γ)为极小值点, 第一极小值能量最低, 对应基态位置
Table 1. The minima of the potential energy surfaces. The coordinates (β, γ) specify the locations of these minima. The primary minimum, which is the deepest, corresponds to the ground state of the nucleus.
原子核 第一极小值 第二极小值 实验四极形变值β 62Zn (0.25, 20) 无 0.216 64Zn (0.23, 0) (0.24, 60) 0.236 70Zn (0, 0) 无 0.216 64Ge (0.26, 27) 无 0.259 66Ge (0.25, 60) (0.24, 0) 0.172 72Ge (0, 0) (0.21, 60) 0.240 66Se (0.26, 60) (0.25, 0) 68Se (0.27, 60) (0.25, 0) 0.242 74Se (0.22, 60) (0, 0) 0.302 68Kr (0.27, 38) 无 70Kr (0.30, 60) (0.25, 0) 76Kr (0, 0) (0.19, 60) 0.290 -
[1] Singh P, Korten W, Hagen T W, Gorgen A, Grente L, Salsac M D, Farget F, Clément E, de France G, Braunroth T, Bruyneel B, Celikovic I, Delaune O, Dewald A, Dijon A 2018 Phys. Rev. Lett. 121 192501
 Google Scholar
Google Scholar
[2] Abusara H, Ahmad S 2017 Phys. Rev. C 96 064303
[3] Cejnar P, Jolie J, Casten R F 2010 Rev. Mod. Phys. 82 2155
 Google Scholar
Google Scholar
[4] Norman E B, Drobizhev A, Gharibyan N, Gregorich K E, Kolomensky Yu G, Sammis B N, Scielzo N D, Shusterman J A, Thomas K J 2024 Phys. Rev. C 109 055501
 Google Scholar
Google Scholar
[5] Majola S N T, Shi Z, Song B Y, Li Z P, Zhang S Q, Bark R A, Sharpey-Schafer J F, Aschman D G, Bvumbi S P, Bucher T D, Cullen D M, Dinoko T S, Easton J E, Erasmus N, Greenlees P T 2019 Phys. Rev. C 100 044324
 Google Scholar
Google Scholar
[6] Yang Y L, Zhao P W, Li Z P 2023 Phys. Rev. C 107 024308
 Google Scholar
Google Scholar
[7] Hua H, Wu C Y, Cline D, Hayes A B, Teng R, Clark R M, Fallon P, Goergen A, Macchiavelli A O, Vetter K 2004 Phys. Rev. C 69 014317
 Google Scholar
Google Scholar
[8] Cwiok S, Heenen P H, Nazarewicz W 2005 Nature 433 705
 Google Scholar
Google Scholar
[9] Ayangeakaa A D, Janssens R V F, Wu C Y, Allmond J M, Wood J L, Zhu S, Albers M, Almaraz-Calderon S, Bucher B, Carpenter M P, Chiara C J, Cline D, Crawford H L, Harker J, Hayes A B, Hoffman C R, Kay B P, Kolos K, Korichi A 2016 Phys. Lett. B 754 254
 Google Scholar
Google Scholar
[10] 圣宗强, 郭建友 2008 57 1557
 Google Scholar
Google Scholar
Sheng Z Q, Guo J Y 2008 Acta Phys. Sin. 57 1557
 Google Scholar
Google Scholar
[11] 焦朋, 郭建友, 方向正 2010 59 2369
 Google Scholar
Google Scholar
Jiao P, Guo J Y, Fang X Z 2010 Acta Phys. Sin. 59 2369
 Google Scholar
Google Scholar
[12] 王刚, 方向正, 郭建友 2012 61 102101
 Google Scholar
Google Scholar
Wang G, Fang X Z, Guo J Y 2012 Acta Phys. Sin. 61 102101
 Google Scholar
Google Scholar
[13] Nomura K, Rodriguez-Guzman R, Robledo L M 2016 Phys. Rev. C 94 044314
 Google Scholar
Google Scholar
[14] Karim A, Siddiqui T A, Ahmad S 2022 Phys. At. Nucl. 85 588
 Google Scholar
Google Scholar
[15] Zhang X Y, Niu Z M, Sun W, Xia X W 2023 Phys. Rev. C 108 024310
[16] Garcia-Ramos J E, Arias J M, Dukelsky J 2014 Phys. Lett. B 736 333
 Google Scholar
Google Scholar
[17] 童红, 张春梅, 石筑一, 汪红, 倪绍勇 2010 59 3136
 Google Scholar
Google Scholar
Tong H, Zhang C, Shi Z Y, Wang H, Ni S Y 2010 Acta Phys. Sin. 59 3136
 Google Scholar
Google Scholar
[18] Bonatsos D, Assimakis I E, Minkov N, Martinou A 2017 Phys. Rev. C 95 064326
 Google Scholar
Google Scholar
[19] 支启军 2011 60 052101
 Google Scholar
Google Scholar
Zhi Q J 2011 Acta Phys. Sin. 60 052101
 Google Scholar
Google Scholar
[20] Wu X H, Ren Z X, Zhao P W 2022 Phys. Rev. C 105 L031303
[21] Gupta S, Bakshi R, Gupta S, Singh S, Bharti A, Bhat G H, Sheikh J A 2023 Eur. Phys. J. A 59 258
 Google Scholar
Google Scholar
[22] 卢希庭, 江栋兴, 叶沿林 2000 原子核物理(北京: 原子能出版社)第192页
Lu X T, Jiang D X, Ye Y L 2000 Nuclear Physics (Beijing: Atomic Energy Press) p192
[23] Wienholtz F, Beck D, Blaum K, Borgmann C, Breitenfeldt M, Cakirli R B, George S, Herfurth F, Holt J D, Kowalska M, Kreim S, Lunney D, Manea V, Menendez J, Neidherr D, Rosenbusch M, Schweikhard L, Schwenk A, Simonis J, Stanja J, Wolf R N, Zuber K 2013 Nature 498 346
 Google Scholar
Google Scholar
[24] Steppenbeck D, Takeuchi S, Aoi N, Doornenbal P, Matsushita M, Wang H, Baba H, Fukuda N, Go S, Honma M, Lee J, Matsui K, Michimasa S, Motobayashi T, Nishimura D, Otsuka T, Sakurai H, Shiga Y, Soderstrom P A, Sumikama T, Suzuki H, Taniuchi R, Utsuno Y, Valiente-Dobon J J, Yoneda K 2013 Nature 502 207
 Google Scholar
Google Scholar
[25] Michimasa S, Kobayashi M, Kiyokawa Y, Ota S, Ahn D S, Baba H, Berg G P A, Dozono M, Fukuda N, Furuno T, Ideguchi E, Inabe N, Kawabata T, Kawase S, Kisamori K, Kobayashi K, Kubo T, Kubota Y, Lee C S, Matsushita M, Miya H, Mizukami A, Nagakura H, Nishimura D, Oikawa H, Sakai H, Shimizu Y, Stolz A, Suzuki H, Takaki M, Takeda H, Takeuchi S, Tokieda H, Uesaka T, Yako K, Yamaguchi Y, Yanagisawa Y, Yokoyama R, Yoshida K, Shimoura S 2018 Phys. Rev. Lett. 121 022506
 Google Scholar
Google Scholar
[26] Liu J, Niu Y F, Long W H 2020 Phys. Lett. B 806 135524
 Google Scholar
Google Scholar
[27] Zhang W, Huang J K, Sun T T, Peng J, Zhang S Q 2024 Chin. Phys. C 48 104105
 Google Scholar
Google Scholar
[28] Ring P 1996 Prog. Part. Nucl. Phys. 37 193
 Google Scholar
Google Scholar
[29] Vretenar D, Afanasjev A V, Lalazissis G A, Ring P 2005 Phys. Rep. 409 101
 Google Scholar
Google Scholar
[30] Meng J, Toki H, Zhou S G, Zhang S Q, Long W H, Geng L S 2006 Prog. Part. Nucl. Phys. 57 470
 Google Scholar
Google Scholar
[31] Liang H Z, Meng J, Zhou S G 2015 Phys. Rep. 570 1
 Google Scholar
Google Scholar
[32] Niksic T, Paar N, Vretenar D, Ring P 2014 Comput. Phys. Commun. 185 1808
 Google Scholar
Google Scholar
[33] Ring P, Schuck P 1981 Phys. Today 36 70
[34] Staszack A, Stoitsov M, Baran A, Nazarewicz W 2010 Eur. Phys. J. A 46 85
 Google Scholar
Google Scholar
[35] Tian Y, Ma Z Y, Ring P 2009 Phys. Lett. B 676 44
 Google Scholar
Google Scholar
[36] Niksic T, Ring P, Vretenar D, Tian Y, Ma Z Y 2010 Phys. Rev. C 81 054318
 Google Scholar
Google Scholar
[37] 沈水法, 王华磊, 孟海燕, 阎玉鹏, 沈洁洁, 王飞鹏, 蒋海滨, 包莉娜 2021 70 192101
 Google Scholar
Google Scholar
Shen S F, Wang H L, Meng H Y, Yan Y P, Shen J J, Wang F P, Jiang H B, Bao L N 2021 Acta Phys. Sin. 70 192101
 Google Scholar
Google Scholar
[38] Wang M, Huang W J, Kondev F G, Audi G, Naimi S 2021 Chin. Phys. C 45 030003
 Google Scholar
Google Scholar
[39] Wang S J, Kanellakopoulos A, Yang X F, Bai S W, Billowes J, Bissell M L, Blaum K, Cheal B, Devlin C S, Garcia Ruiz R F, Han J Z, Heylen H, Kaufmann S, König K, Koszorús Á, Lechner S, Malbrunot-Ettenauer S, Nazarewicz W, Neugart R, Neyens G, Nörtershäuser W, Ratajczyk T, Reinhard P G, Rodríguez L V, Sels S, Xie L, Xu Z Y, Yordanov D T, Yu Y M 2024 Phys. Lett. B 856 138867
 Google Scholar
Google Scholar
[40] El Adri M, Oulne M 2020 Int. J. Mod. Phys. E 29 2050089
[41] 陈翠红, 李占奎, 王秀华, 李荣华, 方芳, 王柱生, 李海霞 2023 72 122902
 Google Scholar
Google Scholar
Chen C H, Li Z K, Wang X H, Li R H, Fang F, Wang Z S, Li H X 2023 Acta Phys. Sin. 72 122902
 Google Scholar
Google Scholar
[42] Liu Y, Wang R, Mushtaq Z, Tian Y , He X H, Qiu H, Chen X R 2025 Chin. Phys. C 49 034103
[43] Enciu M, Liu H N, Obertelli A, Doornenbal P, Nowacki F, Ogata K, Poves A, Yoshida K, Achouri N L 2022 Phys. Rev. Lett. 129 262501
 Google Scholar
Google Scholar
计量
- 文章访问数: 1100
- PDF下载量: 42
- 被引次数: 0













 下载:
下载: