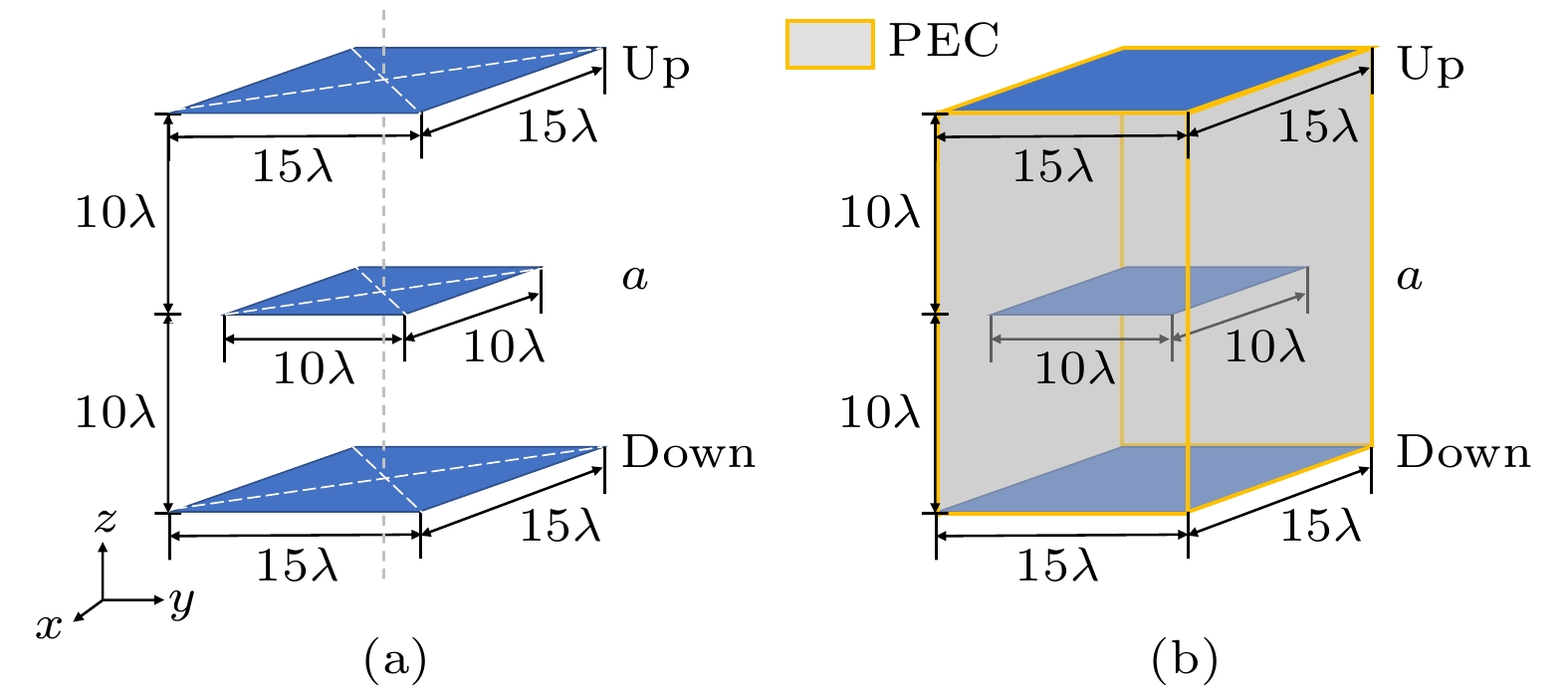
-
With the integration of electromagnetic devices, the modules that make up into the devices and the functions that the devices needed to achieve are becoming more and more diverse. The coupling between the modules is difficult to ignore, the difficulty in designing increases sharply, and the traditional design methods gradually become incompetent. It is urgent to find a new comprehensive electromagnetic design method. This paper is to use the spatiotemporally synchronous focusing characteristics of time-reversed electromagnetic waves to explore the possibility of applying time-reversal technique to device design. First, based on the general device inverse design process, using the time-reversal technique, dyadic Green's function and basic principle of electromagnetics, a method of converting the port field distribution into the internal field distribution of the device is proposed. It is also proved that the continuous equivalent source obtained by the time-reversed field at a certain position in space can produce a field distribution close to the desired field at the port. In the single frequency inverse design process, only the tangential component of the electric field or magnetic field of the port is needed to be known. Then, with the help of the reciprocity of Green's function, the above theory is transformed to facilitate the numerical simulation. This numerical simulation realizes the reconstruction of the amplitude distribution source and the phase distribution source. It should be noted that the amplitude distribution source and phase distribution source are both randomly constructed. The numerical simulation verification is completed in two different cases and a variety of different initial conditions. All the simulation results are consistent with the theoretical results, which proves that it is feasible to apply time-reversal technique to the inverse design of electromagnetic devices.
-
Keywords:
- time-reversal /
- inverse design /
- Green's function
[1] Molesky S, Lin Z, Piggott A Y, Jin W, Vucković J, Rodriguez A W 2018 Nat. Photonics 12 659
Google Scholar
[2] Zhu Y, Ju Y, Zhang C 2019 P. I. Mech. Eng. A-J. Pow. 233 431
[3] Brown T, Narendra C, Vahabzadeh Y, Caloz C, Mojabi P 2020 IEEE Trans. Antennas Propag. 68 1812
Google Scholar
[4] Piggott A Y, Lu J, Lagoudakis K G, Petykiewicz J, Babinec T M, Vučković J 2015 Nat. Photonics 9 374
Google Scholar
[5] Wang M Y, Wang X, Guo D 2003 Comput. Methods Appl. Mech. Eng. 192 227
Google Scholar
[6] Lee H, Itoh T 1997 IEEE Trans. Microw. Theory Tech. 45 803
Google Scholar
[7] Su L, Piggott A Y, Sapra N V, Petykiewicz J A, Vuckovic J 2018 ACS Photonics 5 301
Google Scholar
[8] Su L, Vercruysse D, Skarda J, Sapra N V, Petykiewicz J A, Vučković J 2020 Appl. Phys. Rev. 7 011407
Google Scholar
[9] Callewaert F, Aydin K 2016 Novel Optical Systems Design and Optimization XIX. (San Diego: International Society for Optics and Photonics) p9948
[10] Wang J, Yang X S, Wang B Z 2017 IET Microw. Antennas P. 12 385
[11] Wang J, Yang X S, Ding X, Wang B Z 2018 IEEE Trans. Antennas Propag. 66 2254
Google Scholar
[12] Wang L, Wang G, Sidén J 2015 IEEE Trans. Microw. Theory Tech. 63 3962
Google Scholar
[13] Pehlivanoglu Y V 2014 Appl. Soft Comput. 24 781
Google Scholar
[14] Chen C T, Gu G X 2020 Adv. Sci. 7 1902607
Google Scholar
[15] Salucci M, Gelmini A, Oliveri G, Anselmi N, Massa A 2018 IEEE Trans. Antennas Propag. 66 5805
Google Scholar
[16] Wigner E P 1959 Group Theory and Its Application to the Quantum Mechanics of Atomic Spectra (New York: Academic Press)
[17] 王秉中, 王任 2019 时间反演电磁学 (北京: 科学出版社)
Wang B Z, Wang R 2019 Time-Reversed Electromagnetics (Beijing: Science Press) (in Chinese)
[18] Oestges C, Kim A D, Papanicolaou G, Paulraj A J 2005 IEEE Trans. Antennas Propag. 53 283
Google Scholar
[19] Qiu R C 2006 IEEE Trans. Wirel. Commun. 5 2685
Google Scholar
[20] Gong Z S, Wang B Z, Yang Y, Zhou H C, Ding S, Wang X H 2017 IEEE Photonics J. 9 6900108
[21] Davy M, de R J, Joly J C, Fink M 2010 Phys. Rev. C 11 37
[22] Bacot V, Labousse M, Eddi A, Fink M, Fort E 2016 Nat. Phys. 12 972
Google Scholar
[23] Vahabzadeh Y, Achouri K, Caloz C 2016 IEEE Trans. Antennas Propag. 64 4753
Google Scholar
[24] 龚志双, 王秉中, 王任 2018 67 084101
Google Scholar
Gong Z S Wang B Z, Wang R 2018 Acta Phys. Sin. 67 084101
Google Scholar
[25] Harrington R F 2001 Time-Harmonic Electromagnetic Fields (New York: Wiley-IEEE Press) pp106−110
-
图 1 空间拓扑关系
Figure 1. Topological relation of space.
图 2 用于数值验证的问题转化示意图 (a)数理模型对应的数值验证模型; (b)利用互易原理转换后的数值验证模型
Figure 2. A problem transformation diagram for numerical validation: (a) Numerical verification model corresponding to mathematical model; (b) numerical verification model converted by reciprocity principle.
图 3 数值仿真实验示意图 (a)自由空间验证示意图; (b)四周为理想电导体边界的验证示意图
Figure 3. Schematic diagram of numerical simulation experiment: (a) Schematic diagram of free space verification; (b) schematic diagram of verification of PEC boundaries around.
图 4 重建源代价函数计算结果
Figure 4. The calculation results of the cost function of the rebuild source.
图 5 初始源幅相分布图 (a)
$ {Ex} $ 相位分布为特定函数; (b)$ {Ex} $ 幅度分布为特定函数Figure 5. The amplitude-phase distribution of the original source: (a) The phase distribution is a special function; (b) the amplitude distribution is a special function.
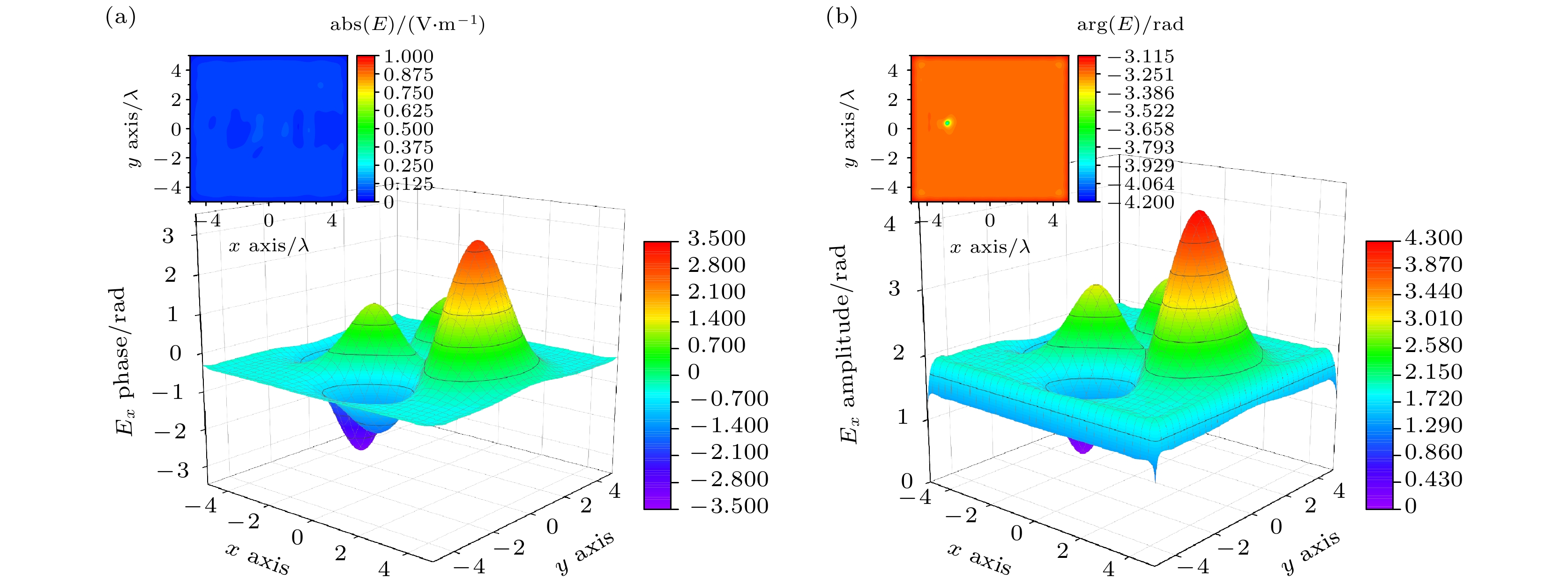
图 6 自由空间条件下重建源的幅相分布 (a)序号为5的重建
$ {{{\mathit{\boldsymbol{f}}}}}_{{Ex}\text{Phase}}^{a}\left(x, y\right) $ 的幅相分布; (b) 序号为8的重建$ {{{\mathit{\boldsymbol{f}}}}}_{{Ex}\text{Phase}}^{a}\left(x, y\right) $ 的幅相分布; (c)序号为2的重建$ {{{\mathit{\boldsymbol{f}}}}}_{{Ex}\text{Amplitude}}^{a}\left(x, y\right) $ 的幅相分布; (d)序号为8的重建$ {{{\mathit{\boldsymbol{f}}}}}_{{Ex}\text{Amplitude}}^{a}\left(x, y\right) $ 的幅相分布Figure 6. The amplitude-phase distribution of the reconstructed source in free space: (a) The amplitude-phase distribution of the reconstructed
$ {{{\mathit{\boldsymbol{f}}}}}_{{Ex{\rm{Phase}}}}^{a}\left(x, y\right) $ with experimental number 5; (b) the amplitude-phase distribution of the reconstructed$ {{{\mathit{\boldsymbol{f}}}}}_{{Ex{\rm{Phase}}}}^{a}\left(x, y\right) $ with experimental number 8; (c) the amplitude-phase distribution of the reconstructed$ {{{\mathit{\boldsymbol{f}}}}}_{{Ex}\text{Amplitude}}^{a}\left(x, y\right) $ with experimental number 2; (d) the amplitude-phase distribution of the reconstructed$ {{{\mathit{\boldsymbol{f}}}}}_{{Ex}\text{Amplitude}}^{a}\left(x, y\right) $ with experimental number 8.
图 7 四周为理想电导体条件下重建源的幅相分布 (a)序号为4的重建
$ {{{\mathit{\boldsymbol{f}}}}}_{{Ex}\text{Phase}}^{a}\left(x, y\right) $ 的幅相分布; (b) 序号为7的重建$ {{{\mathit{\boldsymbol{f}}}}}_{{Ex}\text{Phase}}^{a}\left(x, y\right) $ 的幅相分布; (c)序号为3的重建$ {{{\mathit{\boldsymbol{f}}}}}_{{Ex}\text{Amplitude}}^{a}\left(x, y\right) $ 的幅相分布; (d)序号为9的重建$ {{{\mathit{\boldsymbol{f}}}}}_{{Ex}\text{Amplitude}}^{a}\left(x, y\right) $ 的幅相分布Figure 7. The amplitude-phase distribution of the reconstructed source in PEC space: (a) The amplitude-phase distribution of the reconstructed
$ {{{\mathit{\boldsymbol{f}}}}}_{{Ex}\text{Phase}}^{a}\left(x, y\right) $ with experimental number 4; (b) the amplitude-phase distribution of the reconstructed$ {{{\mathit{\boldsymbol{f}}}}}_{{Ex}\text{Phase}}^{a}\left(x, y\right) $ with experimental number 7; (c) the amplitude-phase distribution of the reconstructed$ {{{\mathit{\boldsymbol{f}}}}}_{{Ex}\text{Amplitude}}^{a}\left(x, y\right) $ with experimental number 3; (d) the amplitude-phase distribution of the reconstructed$ {{{\mathit{\boldsymbol{f}}}}}_{{Ex}\text{Amplitude}}^{a}\left(x, y\right) $ with experimental number 9.表 1 数值仿真结果表
Table 1. Table of numerical simulation results.
序号 使用的反演源 Field域 FPCF FACF PPCF PACF 1 ${ { {\cal{F} } }_{{field} }^{ \xi \text{, up} } }^{*}$ ${field}=\{ {Ex}, {Ey}, {Ez}, {Hx}, {Hy}, {Hz}\}$ 0.0077 0.0647 0.0189 0.0712 2 ${field}=\{ {Ex}, {Ey}, {Ez}\}$ 0.0086 0.0784 0.0085 0.0735 3 ${field}=\{ {Ex}, {Ey}\}$ 0.0082 0.0750 0.0085 0.0735 4 ${ { {\cal{F} } }_{{field} }^{ \xi \text{, down} } }^{*}$ ${field}=\{ {Ex, }{Ey}, {Ez}, {Hx}, {Hy}, {Hz}\}$ 0.0081 0.0624 0.0191 0.0735 5 ${field}=\{ {Ex}, {Ey}, Ez\}$ 0.0092 0.0703 0.0098 0.0707 6 ${field}=\{ {Ex}, {Ey}\}$ 0.0088 0.0668 0.0098 0.0707 7 ${ { {\cal{F} } }_{{field} }^{ \xi \text{, up} } }^{*}$, ${ { {\cal{F} } }_{{field} }^{ \xi \text{, down} } }^{*}$ ${field}=\{ {Ex}, {Ey}, {Ez}, {Hx}, {Hy}, {Hz}\}$ 0.0078 0.0635 0.0189 0.0713 8 ${field}=\{ {Ex}, {Ey}, {Ez}\}$ 0.0087 0.0747 0.0090 0.0718 9 ${field}=\{ {Ex}, {Ey}\}$ 0.0083 0.0712 0.0090 0.0718 
DownLoad: CSV
-
[1] Molesky S, Lin Z, Piggott A Y, Jin W, Vucković J, Rodriguez A W 2018 Nat. Photonics 12 659
Google Scholar
[2] Zhu Y, Ju Y, Zhang C 2019 P. I. Mech. Eng. A-J. Pow. 233 431
[3] Brown T, Narendra C, Vahabzadeh Y, Caloz C, Mojabi P 2020 IEEE Trans. Antennas Propag. 68 1812
Google Scholar
[4] Piggott A Y, Lu J, Lagoudakis K G, Petykiewicz J, Babinec T M, Vučković J 2015 Nat. Photonics 9 374
Google Scholar
[5] Wang M Y, Wang X, Guo D 2003 Comput. Methods Appl. Mech. Eng. 192 227
Google Scholar
[6] Lee H, Itoh T 1997 IEEE Trans. Microw. Theory Tech. 45 803
Google Scholar
[7] Su L, Piggott A Y, Sapra N V, Petykiewicz J A, Vuckovic J 2018 ACS Photonics 5 301
Google Scholar
[8] Su L, Vercruysse D, Skarda J, Sapra N V, Petykiewicz J A, Vučković J 2020 Appl. Phys. Rev. 7 011407
Google Scholar
[9] Callewaert F, Aydin K 2016 Novel Optical Systems Design and Optimization XIX. (San Diego: International Society for Optics and Photonics) p9948
[10] Wang J, Yang X S, Wang B Z 2017 IET Microw. Antennas P. 12 385
[11] Wang J, Yang X S, Ding X, Wang B Z 2018 IEEE Trans. Antennas Propag. 66 2254
Google Scholar
[12] Wang L, Wang G, Sidén J 2015 IEEE Trans. Microw. Theory Tech. 63 3962
Google Scholar
[13] Pehlivanoglu Y V 2014 Appl. Soft Comput. 24 781
Google Scholar
[14] Chen C T, Gu G X 2020 Adv. Sci. 7 1902607
Google Scholar
[15] Salucci M, Gelmini A, Oliveri G, Anselmi N, Massa A 2018 IEEE Trans. Antennas Propag. 66 5805
Google Scholar
[16] Wigner E P 1959 Group Theory and Its Application to the Quantum Mechanics of Atomic Spectra (New York: Academic Press)
[17] 王秉中, 王任 2019 时间反演电磁学 (北京: 科学出版社)
Wang B Z, Wang R 2019 Time-Reversed Electromagnetics (Beijing: Science Press) (in Chinese)
[18] Oestges C, Kim A D, Papanicolaou G, Paulraj A J 2005 IEEE Trans. Antennas Propag. 53 283
Google Scholar
[19] Qiu R C 2006 IEEE Trans. Wirel. Commun. 5 2685
Google Scholar
[20] Gong Z S, Wang B Z, Yang Y, Zhou H C, Ding S, Wang X H 2017 IEEE Photonics J. 9 6900108
[21] Davy M, de R J, Joly J C, Fink M 2010 Phys. Rev. C 11 37
[22] Bacot V, Labousse M, Eddi A, Fink M, Fort E 2016 Nat. Phys. 12 972
Google Scholar
[23] Vahabzadeh Y, Achouri K, Caloz C 2016 IEEE Trans. Antennas Propag. 64 4753
Google Scholar
[24] 龚志双, 王秉中, 王任 2018 67 084101
Google Scholar
Gong Z S Wang B Z, Wang R 2018 Acta Phys. Sin. 67 084101
Google Scholar
[25] Harrington R F 2001 Time-Harmonic Electromagnetic Fields (New York: Wiley-IEEE Press) pp106−110
DownLoad:
Catalog
Metrics
- Abstract views: 5386
- PDF Downloads: 94
- Cited By: 0
