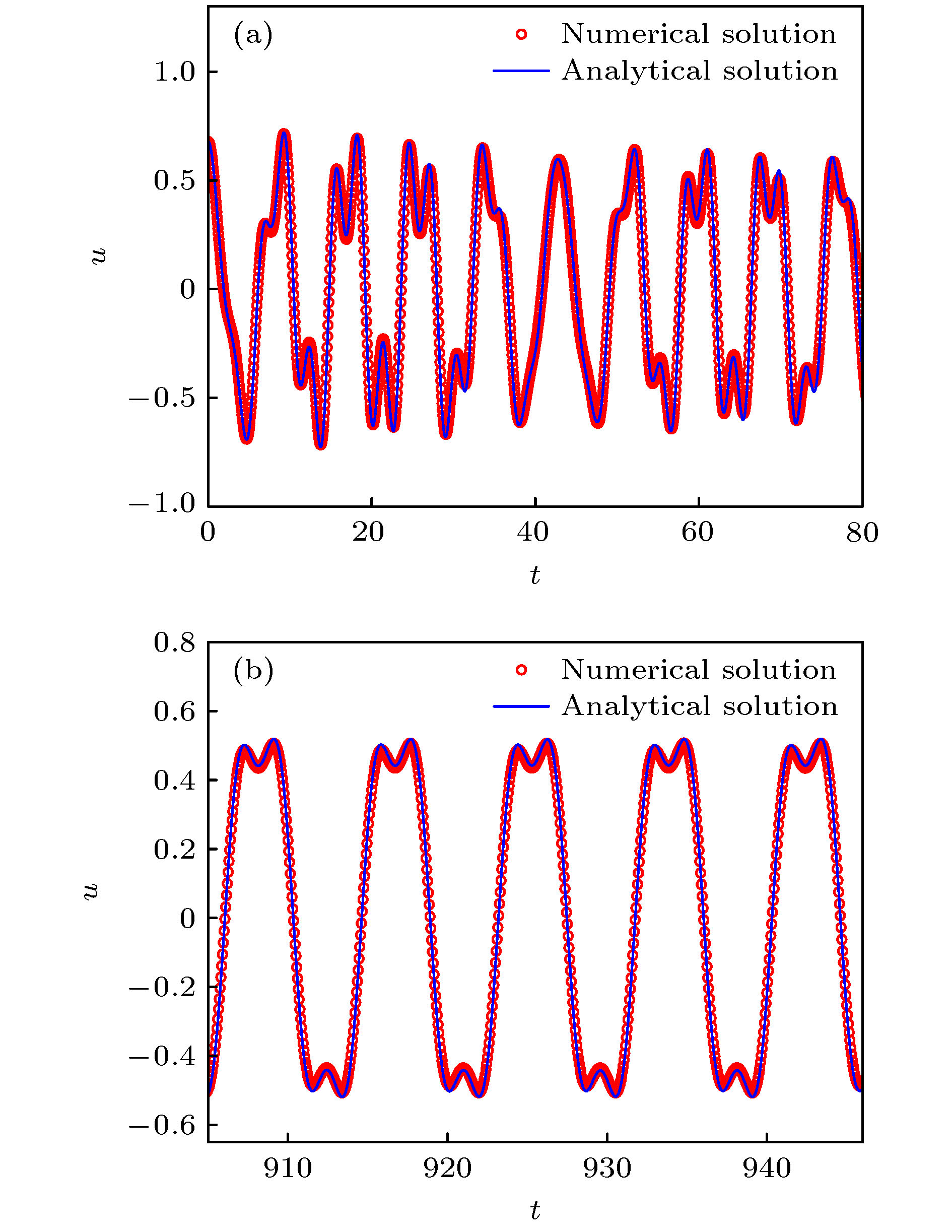
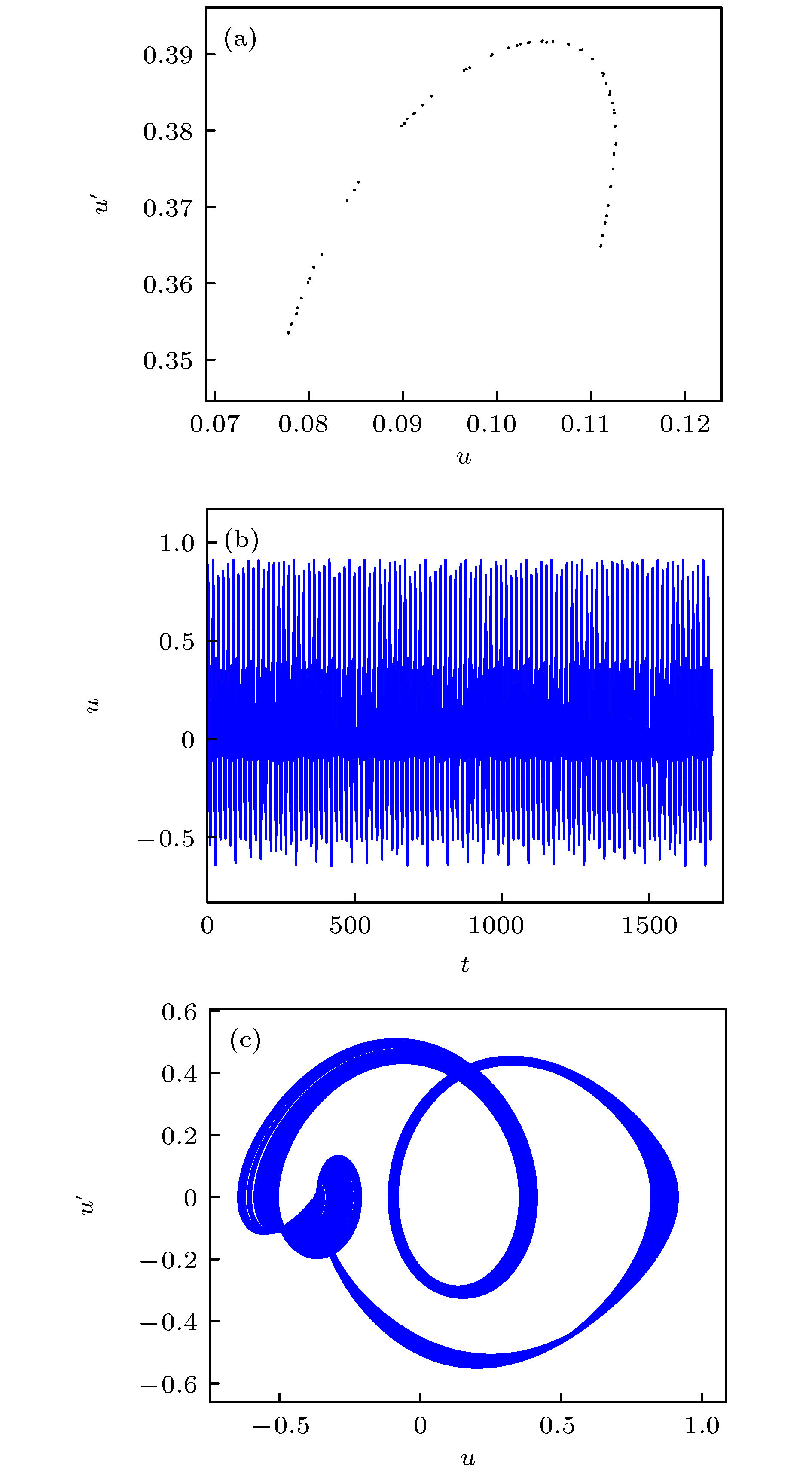
-
There are many resonance phenomena in a nonlinear dynamical system subjected to forced excitation, especially the excitation with multiple frequencies. Duffing oscillator subjected to the excitation with multiple frequencies may exhibit some complex resonance phenomena, such as simultaneous resonance and combination resonance. In this paper, the simultaneous primary and super-harmonic resonance of Duffing oscillator is studied, and it is analyzed in periodic motion and chaotic motion. Firstly, the approximate analytical solution is obtained by the method of multiple scales, and the correctness and accuracy of the analytical solution are verified through numerical simulation. Furthermore, the amplitude-frequency equation and phase-frequency equation of the steady-state response are derived from the approximate solution, and the stability of the steady-state response is analyzed based on Lyapunov’s first method. It is found that there are at most two stable periodic solutions and one unstable periodic solution. The effects of nonlinear stiffness on steady-state response is also analyzed through numerical simulation. However, the approximate solution obtained by the singular perturbation method is not sufficient to describe the global characteristics of the system, therefore, the necessary condition for the chaos in the sense of Smale horseshoes is derived based on the Melnikov method. Finally, one-demonstrational system that meets the condition of simultaneous resonance is analyzed through numerical simulation, and the bifurcation diagram shows the two thresholds of the demonstration system. At the first threshold, the heteroclinic orbit of the system breaks, and the system goes to chaos in crisis way. At the second threshold, the crisis reappears and the new strange attractor appears. The variation of the first critical value under various frequency combinations is investigated based on the Melnikov method, and the results are compared with the results of numerical simulation. The analytical and numerical results are qualitatively the same although there is a quantitative difference between them.
-
Keywords:
- Duffing system /
- simultaneous resonance /
- nonlinear dynamical system /
- chaos
[1] 孟光, 薛中擎 1989 航空动力学报 2 173
Meng G, Xue Z Q 1989 J. Aerosp. Power 2 173
[2] Ertas A, Chew E K 1990 Int. J. Non Linear Mech. 25 241
Google Scholar
[3] Pan R, Davies H G 1996 Nonlinear Dyn. 9 349
Google Scholar
[4] 刘亚冲 2019 船舶力学 23 135
Google Scholar
Liu Y C 2019 J. Ship Mech. 23 135
Google Scholar
[5] Huan R H, Zhu W Q, Ma F, Ying Z G 2014 Nonlinear Dyn. 76 765
Google Scholar
[6] 宦荣华, 宋亚轻, 朱位秋 2014 浙江大学学报(工学版) 48 321
Huan R H, Song Y Q, Zhu W Q 2014 J. Zhejiang Univ. (Eng. Sci.) 48 321
[7] Hu N Q, Wen X S 2003 J. Sound Vibr. 268 917
Google Scholar
[8] 姚海洋, 王海燕, 张之琛, 申晓红 2017 66 124302
Google Scholar
Yao H Y, Wang H Y, Zhang Z C, Shen X H 2017 Acta Phys. Sin. 66 124302
Google Scholar
[9] 曹保锋, 李鹏, 李小强, 张雪芹, 宁王师, 梁睿, 李欣, 胡淼, 郑毅 2019 68 0805010
Cao B F, Li P, Li X Q, Zhang X Q, Ning W S, Liang R, Li X, Hu M, Zheng Y 2019 Acta Phys. Sin. 68 0805010
[10] Erturk A, Inman D J 2011 J. Sound Vibr. 330 2339
Google Scholar
[11] Wang Y L, Yang Z B, Li P Y, Cao D Q, Huang W H, Inman D J 2020 Nano Energy 75 104853
Google Scholar
[12] Shen Y J, Yang S P, Xing H J, Gao G S 2012 Commun. Nonlinear Sci. Numer. Simul. 17 3092
Google Scholar
[13] Shen Y J, Yang S P, Xing H J, Ma H X 2012 Int. J. Non Linear Mech. 47 975
Google Scholar
[14] Agarwal V, Zheng X, Balachandran B 2018 Phys. Lett. A 382 3355
Google Scholar
[15] 温少芳, 申永军, 杨绍普 2016 65 094502
Google Scholar
Wen S F, Shen Y J, Yang S P 2016 Acta Phys. Sin. 65 094502
Google Scholar
[16] 杨晓丽, 徐伟, 孙中奎 2006 55 1678
Google Scholar
Yang X L, Xu W, Sun Z K 2006 Acta Phys. Sin. 55 1678
Google Scholar
[17] 马少娟, 徐伟, 李伟 2006 55 4013
Google Scholar
Ma S J, Xu W, Li W 2006 Acta Phys. Sin. 55 4013
Google Scholar
[18] 吴存利, 马少娟, 孙中奎, 方同 2006 55 6253
Google Scholar
Wu C L, Ma S J, Sun Z K, Fang T 2006 Acta Phys. Sin. 55 6253
Google Scholar
[19] Niu J C, Liu R Y, Shen Y J, Yang S P 2019 Chaos 29 123106
Google Scholar
[20] Liu X J, Li H, Jiang J, Tang D F, Yang L X 2016 Nonlinear Dyn. 83 1419
Google Scholar
[21] Shen Y J, Wen S F, Li X H, Yang S P, Xing H J 2016 Nonlinear Dyn. 85 1457
Google Scholar
[22] Niu J C, Shen Y J, Yang S P, Li S J 2018 J. Vib. Control 24 3744
Google Scholar
[23] Hassan A 1994 J. Sound Vibr. 172 513
Google Scholar
[24] Van K N, Chien T Q 2016 J. Comput. Nonlinear Dyn. 11 051018
Google Scholar
[25] Yang S P, Nayfeh A H, Mook D T 1998 Acta Mech. 131 235
Google Scholar
[26] 李航, 申永军, 李向红, 韩彦军, 彭孟菲 2020 力学学报 52 514
Google Scholar
Li H, Shen Y J, Li X H, Han Y J, Peng M F 2020 Chin. J. Theor. Appl. Mech. 52 514
Google Scholar
[27] Nayfeh A H, Mook D T 2008 Nonlinear oscillations (New York: John Wiley & Sons) pp162–192
[28] Szemplinska-Stupnicka W, Bajkowski J 1986 Int. J. Non Linear Mech. 21 401
Google Scholar
[29] Van Dooren R 1988 J. Sound Vibr. 123 327
Google Scholar
[30] 毕勤胜, 陈予恕, 吴志强 1998 应用数学和力学 19 113
Bi Q S, Chen Y S, Wu Z Q 1998 Appl. Math. Mech. 19 113
[31] 胡海岩 2000 应用非线性动力学 (北京: 航空工业出版社) 第25−30页
Hu H Y 2000 Applied Nonlinear Dynamics (Beijing: Aviation Industry Press) pp25−30(in Chinese)
[32] Hosea M E, Shampine L F 1996 Appl. Numer. Math. 20 21
Google Scholar
[33] Shampine L F, Reichelt M W, Kierzenka J A 1999 SIAM Rev. 41 538
Google Scholar
[34] Lai D, Chen G 1998 Math. Comput. Modell. 27 1
-
图 1 幅频曲线对比
Figure 1. Comparisons of amplitude-frequency curves.
图 2 位移时间历程对比 (a) 瞬态响应; (b) 稳态响应
Figure 2. Comparisons of displacement time histories: (a) Transient response; (b) steady-state response.
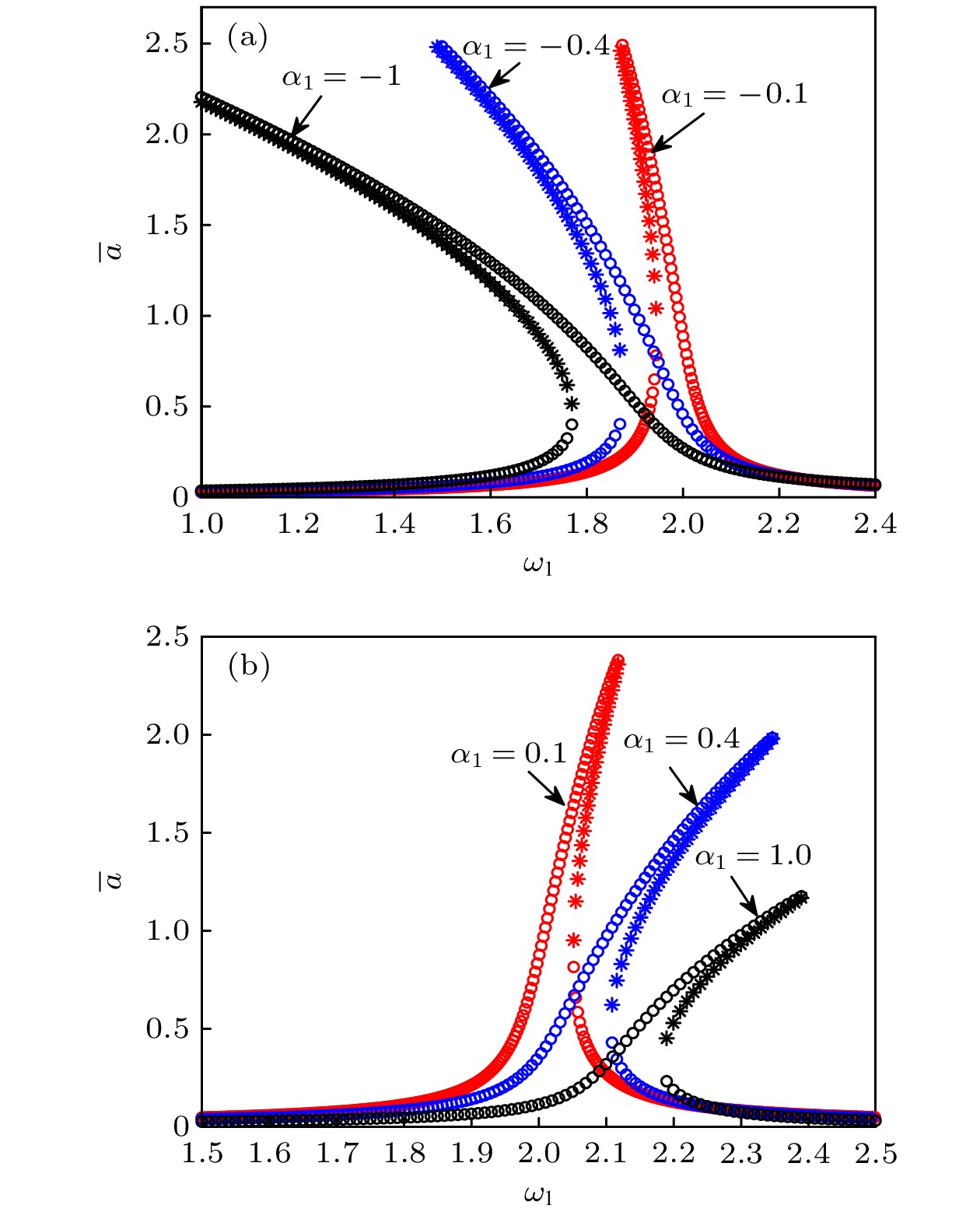
图 3 定常解的幅频曲线 (a)
${\alpha _1} \!=\! - 0.4$ , 刚度软化; (b)${\alpha _1} \!=\! 0.4$ , 刚度硬化 (圆表示稳定解支, 星号表示不稳定解支)Figure 3. Amplitude-frequency curves of steady-state response: (a)
${\alpha _1} = - 0.4$ , stiffness softening; (b)${\alpha _1} = 0.4$ , stiffness hardening (the circles for stable solution and the asterisks for unstable one).
图 4 定常解的相频曲线 (a)
${\alpha _1} \!=\! - 0.4$ , 刚度软化; (b)${\alpha _1} \!= 0.4$ , 刚度硬化(圆表示稳定解支, 星号表示不稳定解支)Figure 4. Phase-frequency curves of steady-state response: (a)
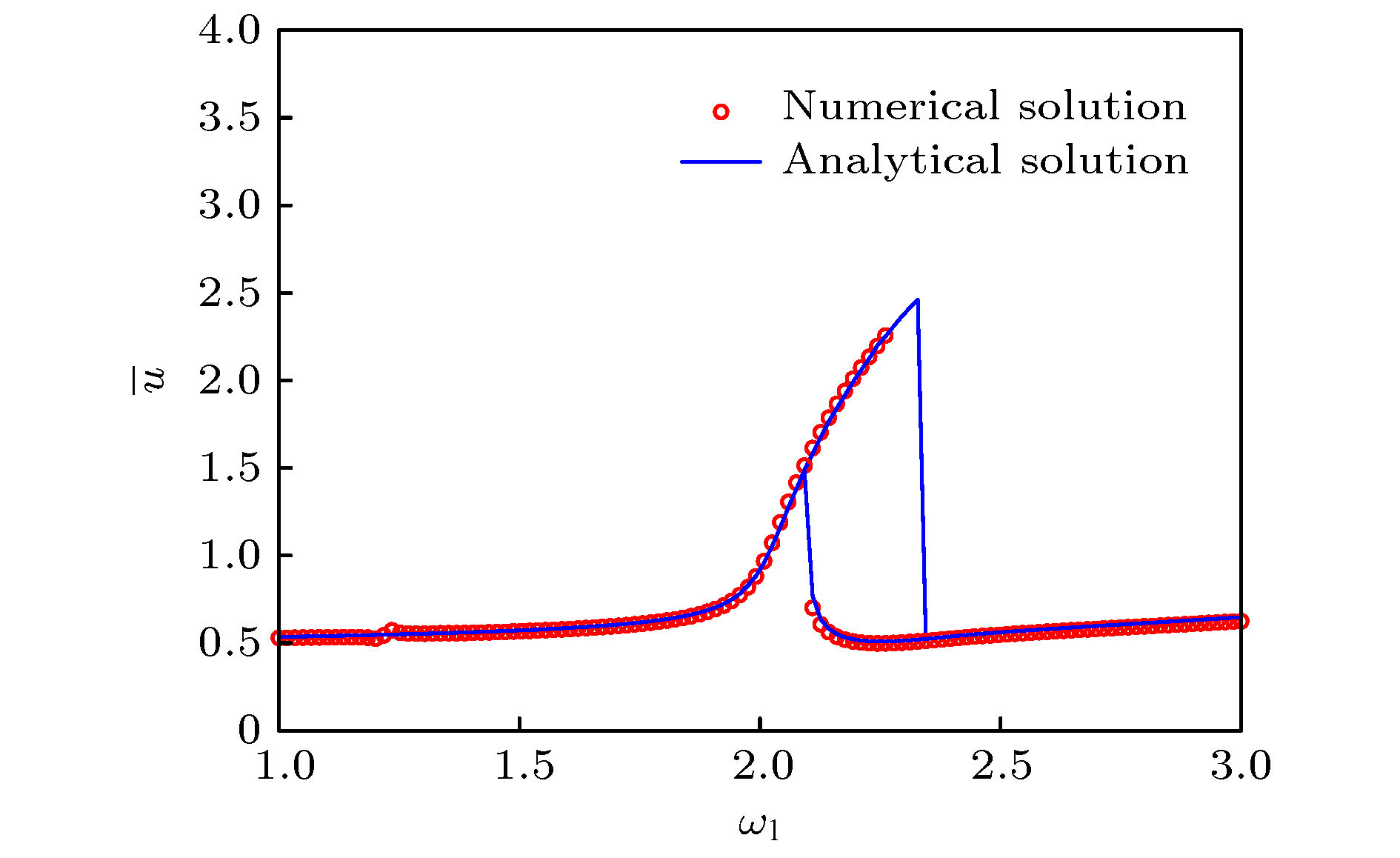
${\alpha _1} = - 0.4$ , stiffness softening; (b)${\alpha _1} = 0.4$ , stiffness hardening (the circles for stable solution and the asterisks for unstable one).
图 5 非线性系数
${\alpha _1}$ 的影响 (a) 刚度软化; (b) 刚度硬化 (圆表示稳定解支, 星号表示不稳定解支)Figure 5. Effects of the nonlinear coefficient
${\alpha _1}$ : (a) Stiffness softening; (b) stiffness hardening (the circles for stable solution and the asterisks for unstable one).
图 8
${F_2} = 0.259$ 时的周期轨道Figure 8. Periodic orbits for
${F_2} = 0.259$ .
图 9
${F_2} = 0.2595$ 时的混沌状态 (a) Poincare截面; (b) 位移时间历程; (c) 相轨迹Figure 9. Chaotic state for
${F_2} = 0.2595$ : (a) Poincare map; (b) displacement time histories; (c) phase trajectory.
图 10
${F_2} = 0.268$ 时的混沌状态 (a) 位移时间历程; (b) 相轨迹Figure 10. Chaotic state for
${F_2} = 0.268$ : (a) Displacement time histories; (b) phase trajectory.
图 11 临界激励幅值
${F_2}$ 的解析结果与数值仿真结果对比 (a)${\omega _1} = 3{\omega _2}$ ; (b)${\omega _1} = 1.1$ ; (c)${\omega _2} = 0.3667$ (星号代表解析结果, 圆代表数值仿真结果)Figure 11. Comparisons of analytical results and numerical simulation results of critical excitation amplitude
${F_2}$ : (a)${\omega _1} = 3{\omega _2}$ ; (b)${\omega _1} = 1.1$ ; (c)${\omega _2} = 0.3667$ (the asterisks for analytical results and the circles for numerical simulation results). -
[1] 孟光, 薛中擎 1989 航空动力学报 2 173
Meng G, Xue Z Q 1989 J. Aerosp. Power 2 173
[2] Ertas A, Chew E K 1990 Int. J. Non Linear Mech. 25 241
Google Scholar
[3] Pan R, Davies H G 1996 Nonlinear Dyn. 9 349
Google Scholar
[4] 刘亚冲 2019 船舶力学 23 135
Google Scholar
Liu Y C 2019 J. Ship Mech. 23 135
Google Scholar
[5] Huan R H, Zhu W Q, Ma F, Ying Z G 2014 Nonlinear Dyn. 76 765
Google Scholar
[6] 宦荣华, 宋亚轻, 朱位秋 2014 浙江大学学报(工学版) 48 321
Huan R H, Song Y Q, Zhu W Q 2014 J. Zhejiang Univ. (Eng. Sci.) 48 321
[7] Hu N Q, Wen X S 2003 J. Sound Vibr. 268 917
Google Scholar
[8] 姚海洋, 王海燕, 张之琛, 申晓红 2017 66 124302
Google Scholar
Yao H Y, Wang H Y, Zhang Z C, Shen X H 2017 Acta Phys. Sin. 66 124302
Google Scholar
[9] 曹保锋, 李鹏, 李小强, 张雪芹, 宁王师, 梁睿, 李欣, 胡淼, 郑毅 2019 68 0805010
Cao B F, Li P, Li X Q, Zhang X Q, Ning W S, Liang R, Li X, Hu M, Zheng Y 2019 Acta Phys. Sin. 68 0805010
[10] Erturk A, Inman D J 2011 J. Sound Vibr. 330 2339
Google Scholar
[11] Wang Y L, Yang Z B, Li P Y, Cao D Q, Huang W H, Inman D J 2020 Nano Energy 75 104853
Google Scholar
[12] Shen Y J, Yang S P, Xing H J, Gao G S 2012 Commun. Nonlinear Sci. Numer. Simul. 17 3092
Google Scholar
[13] Shen Y J, Yang S P, Xing H J, Ma H X 2012 Int. J. Non Linear Mech. 47 975
Google Scholar
[14] Agarwal V, Zheng X, Balachandran B 2018 Phys. Lett. A 382 3355
Google Scholar
[15] 温少芳, 申永军, 杨绍普 2016 65 094502
Google Scholar
Wen S F, Shen Y J, Yang S P 2016 Acta Phys. Sin. 65 094502
Google Scholar
[16] 杨晓丽, 徐伟, 孙中奎 2006 55 1678
Google Scholar
Yang X L, Xu W, Sun Z K 2006 Acta Phys. Sin. 55 1678
Google Scholar
[17] 马少娟, 徐伟, 李伟 2006 55 4013
Google Scholar
Ma S J, Xu W, Li W 2006 Acta Phys. Sin. 55 4013
Google Scholar
[18] 吴存利, 马少娟, 孙中奎, 方同 2006 55 6253
Google Scholar
Wu C L, Ma S J, Sun Z K, Fang T 2006 Acta Phys. Sin. 55 6253
Google Scholar
[19] Niu J C, Liu R Y, Shen Y J, Yang S P 2019 Chaos 29 123106
Google Scholar
[20] Liu X J, Li H, Jiang J, Tang D F, Yang L X 2016 Nonlinear Dyn. 83 1419
Google Scholar
[21] Shen Y J, Wen S F, Li X H, Yang S P, Xing H J 2016 Nonlinear Dyn. 85 1457
Google Scholar
[22] Niu J C, Shen Y J, Yang S P, Li S J 2018 J. Vib. Control 24 3744
Google Scholar
[23] Hassan A 1994 J. Sound Vibr. 172 513
Google Scholar
[24] Van K N, Chien T Q 2016 J. Comput. Nonlinear Dyn. 11 051018
Google Scholar
[25] Yang S P, Nayfeh A H, Mook D T 1998 Acta Mech. 131 235
Google Scholar
[26] 李航, 申永军, 李向红, 韩彦军, 彭孟菲 2020 力学学报 52 514
Google Scholar
Li H, Shen Y J, Li X H, Han Y J, Peng M F 2020 Chin. J. Theor. Appl. Mech. 52 514
Google Scholar
[27] Nayfeh A H, Mook D T 2008 Nonlinear oscillations (New York: John Wiley & Sons) pp162–192
[28] Szemplinska-Stupnicka W, Bajkowski J 1986 Int. J. Non Linear Mech. 21 401
Google Scholar
[29] Van Dooren R 1988 J. Sound Vibr. 123 327
Google Scholar
[30] 毕勤胜, 陈予恕, 吴志强 1998 应用数学和力学 19 113
Bi Q S, Chen Y S, Wu Z Q 1998 Appl. Math. Mech. 19 113
[31] 胡海岩 2000 应用非线性动力学 (北京: 航空工业出版社) 第25−30页
Hu H Y 2000 Applied Nonlinear Dynamics (Beijing: Aviation Industry Press) pp25−30(in Chinese)
[32] Hosea M E, Shampine L F 1996 Appl. Numer. Math. 20 21
Google Scholar
[33] Shampine L F, Reichelt M W, Kierzenka J A 1999 SIAM Rev. 41 538
Google Scholar
[34] Lai D, Chen G 1998 Math. Comput. Modell. 27 1
DownLoad:
Catalog
Metrics
- Abstract views: 6442
- PDF Downloads: 157
- Cited By: 0
