受垂直激励和水平约束的单摆系统亚谐共振分岔与混沌

赵武; 张鸿斌; 孙超凡; 黄丹; 范俊锴

doi:10.7498/aps.70.20210953

摘要

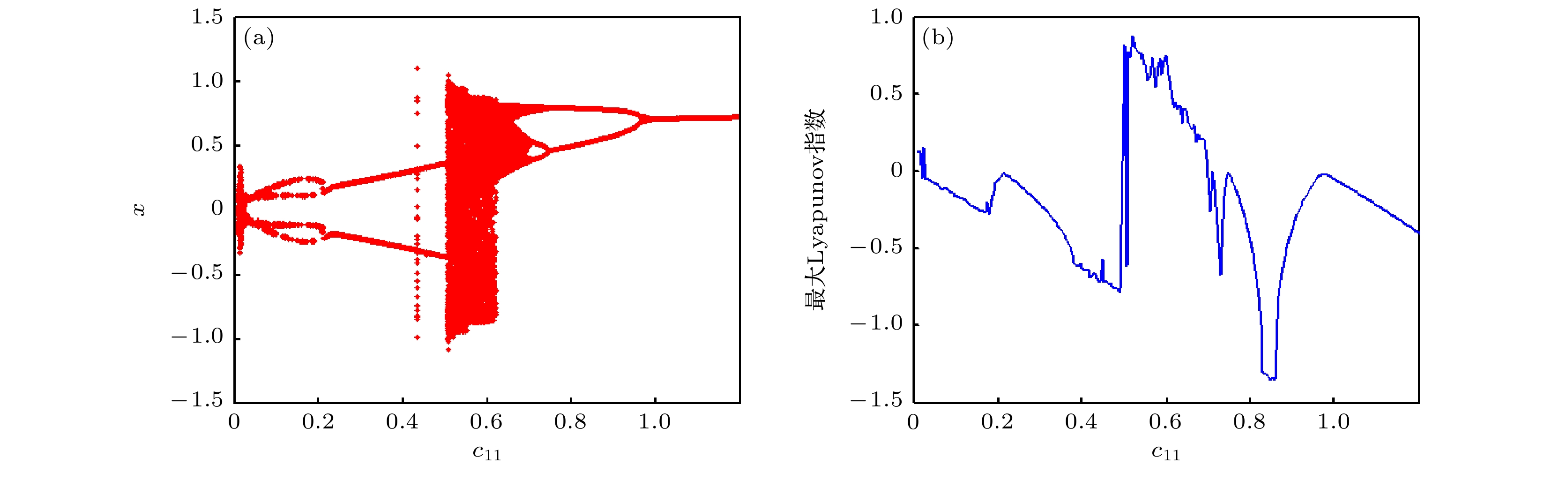
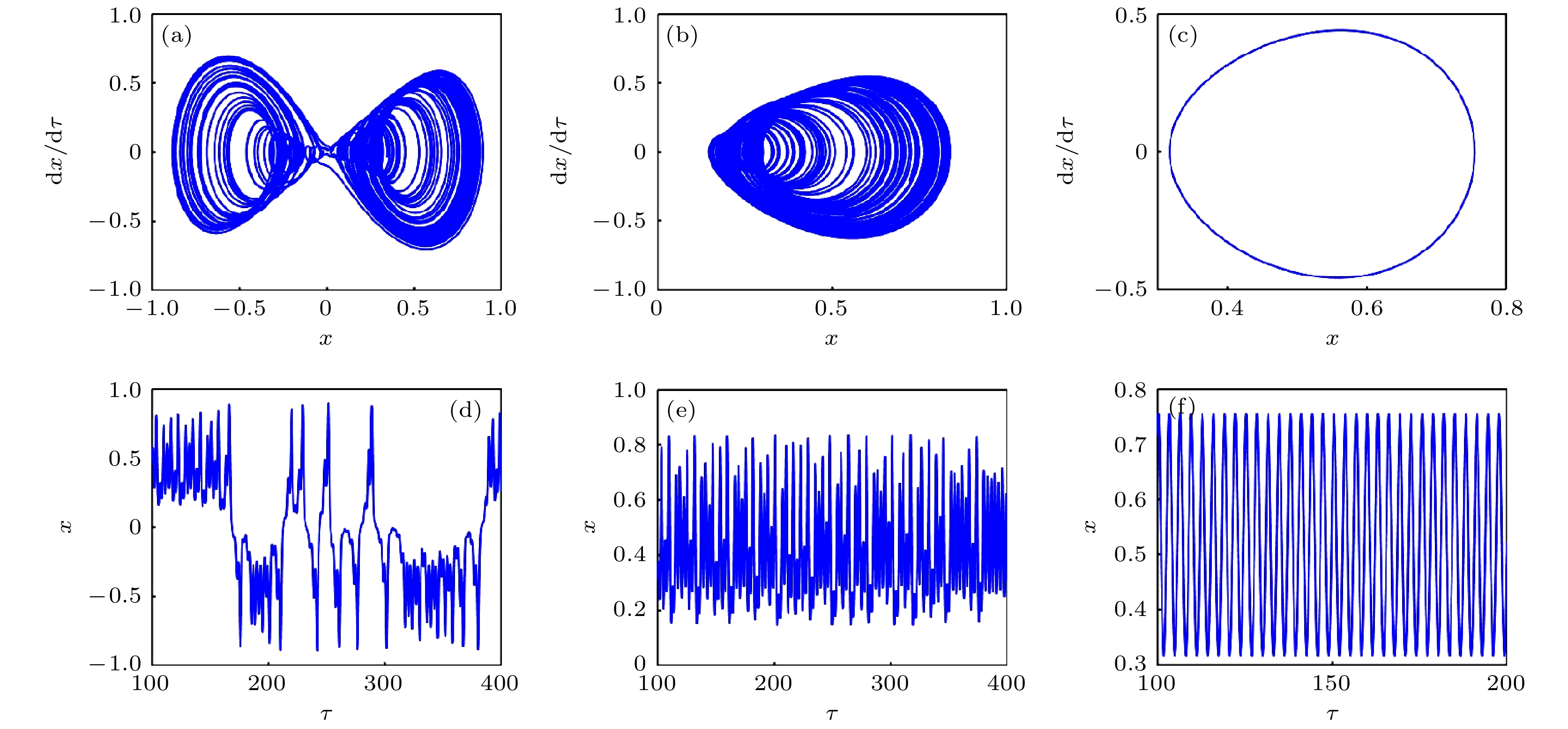
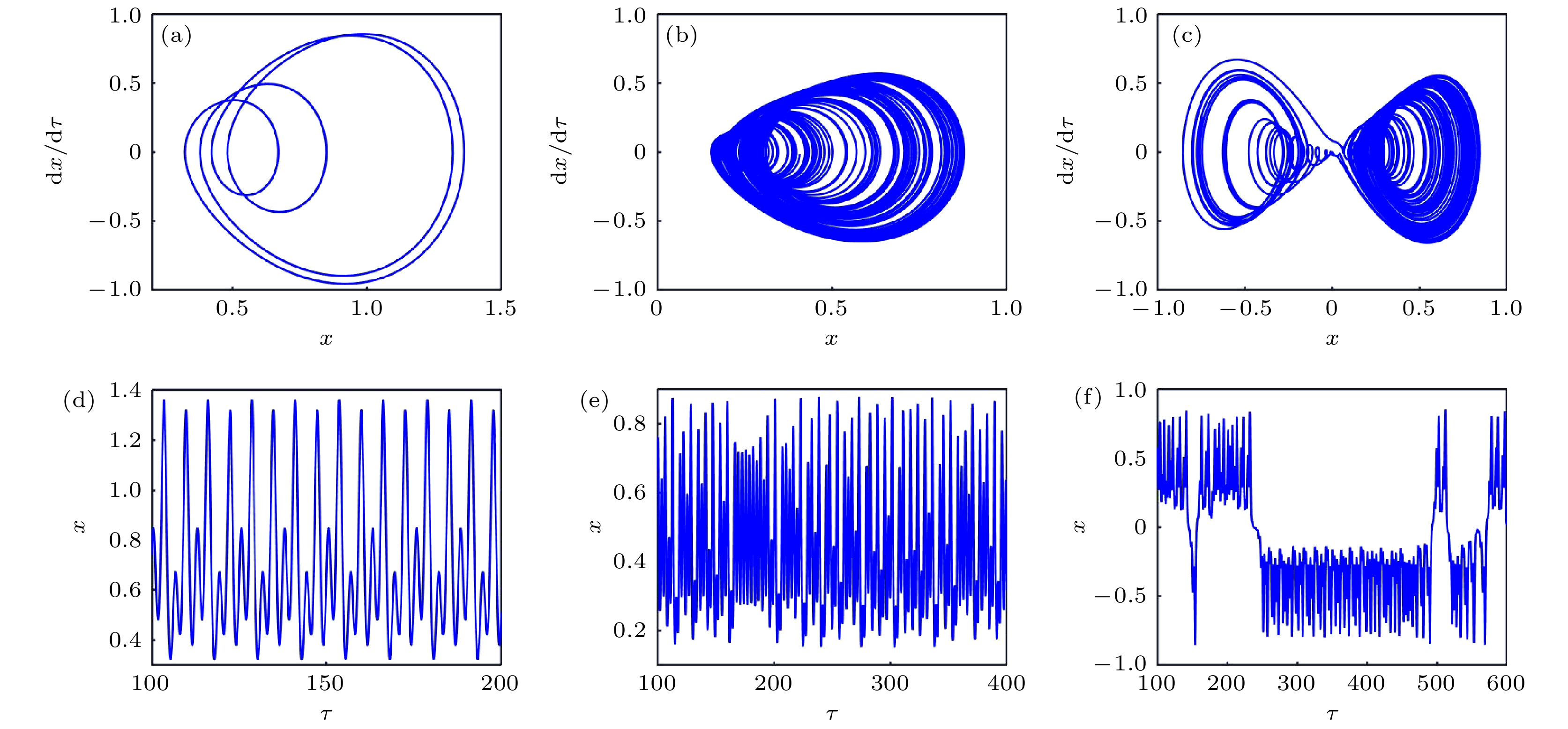
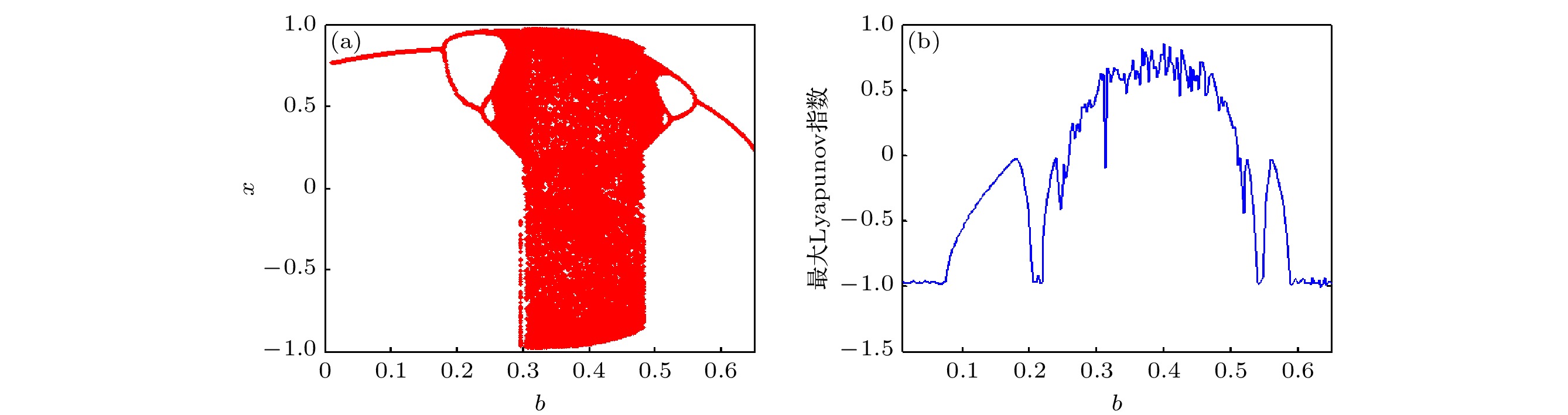
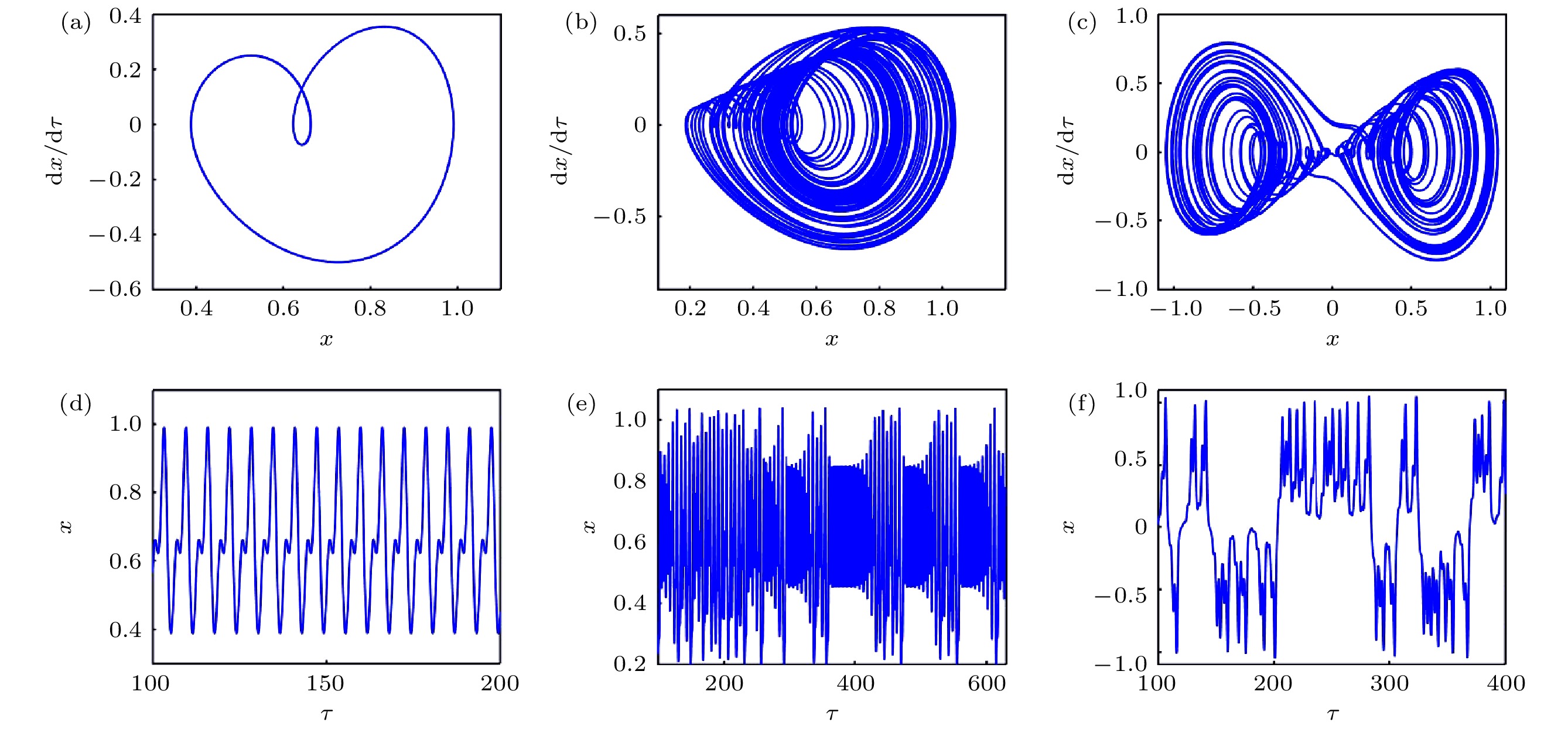
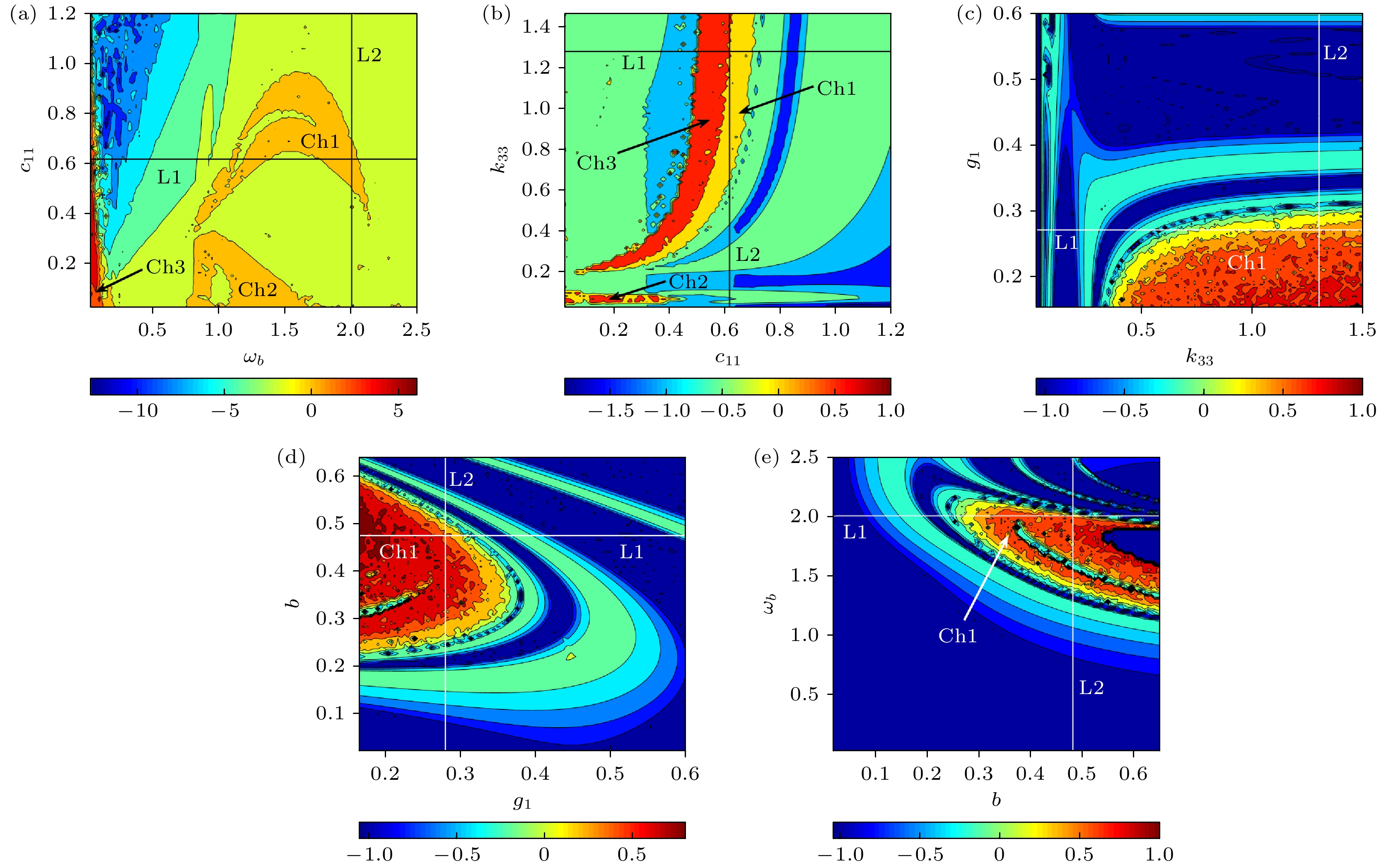
为解决一类典型工程摆的工作性能参数优选, 抽象该类系统为“受垂直激励和水平约束”的物理单摆模型. 运用多尺度法解析系统的亚谐共振响应, 明确了系统参数对幅值共振带宽、多值性的作用规律. 利用Melnikov函数法, 求解得到系统的同宿轨和Smale意义上混沌的阈值条件. 通过数值法解析系统单参分岔、最大Lyapunov指数、双参分岔及吸引域流形转迁等动力特性, 揭示了这类摆系统的亚谐共振分岔、周期吸引子倍增、周期与混沌吸引子共存等全局特性的运动规律, 进一步明确了相关参数改变对系统运动形态转化、能量分布与演变规律的作用机理, 得到了相关参数对工程系统工作性能的影响和作用机制. 研究结果对工程中该类典型物理系统的工作性能参数调整, 及其对实际工况中系统的减振抑振提供了理论依据.

关键词:

单摆 /
亚谐共振 /
分岔 /
混沌

Abstract

In order to improve the working performance and optimize the working parameters of the typical engineering pendulum of a typical system that it is abstracted as a physical simple pendulum model with vertical excitation and horizontal constraint. The dynamical equation of the system with vertical excitation and horizontal constraint is established by using Lagrange equation. The multiple-scale method is used to analyze the subharmonic response characteristics of the system. The amplitude-frequency response equation and the phase-frequency response equation are obtained through calculation. The effects of the system parameters on the amplitude resonance bandwidth and variability are clarified. According to the singularity theory and the universal unfolding theory, the bifurcation topology structure of the subharmonic resonance of the system is obtained. The Melnikov function is applied to the study of the critical conditions for the chaotic motion of the system. The parameter equation of homoclinic orbit motion is obtained through calculation. The threshold conditions of chaos in the sense of Smale are analyzed by solving the Melnikov function of the homoclinic motion orbit. The dynamic characteristics of the system, including single-parameter bifurcation, maximum Lyapunov exponent, bi-parameter bifurcation, and manifold transition in the attraction basin, are analyzed numerically. The results show that the main path of the system entering into the chaos is an almost period doubling bifurcation. Complex dynamical behaviors such as periodic motion, period doubling bifurcation and chaos are found. The bi-parameter matching areas of the subharmonic resonance bifurcation and chaos of the system are clarified. The results reveal the global characteristics of the system with vertical excitation and horizontal constraint, such as subharmonic resonance bifurcation, periodic attractor multiplication, and the coexistence of periodic and chaotic attractors. The results further clarify the mechanism of the influence of system parameters change on the movement form transformation, energy distribution and evolution law of the system. The mechanism of the influence of relevant parameters on the performance of the engineering system with vertical excitation and horizontal constraint is also obtained. The results of this research provide theoretical bases for adjusting the parameters of working performances of this typical physical system in engineering domain and the vibration reduction and suppression of the system in actual working conditions.

Keywords:

作者及机构信息

1.
河南理工大学机械与动力工程学院, 焦作　454003

2.
河南理工大学材料科学与工程学院, 焦作　454003

通信作者: 张鸿斌, zhanghongbin2020@163.com

基金项目: 国家自然科学基金联合基金(批准号: U1604140)、河南省科技攻关计划(批准号: 172102210269, 192102210052, 212102210108, 212102210004)、河南省重大成果培育项目(批准号: NSFRF170503)和河南理工大学创新团队基金(批准号: T2019-5)资助的课题

Authors and contacts

1.
School of Mechanical and Power Engineering, Henan Polytechnic University, Jiaozuo 454003, China

2.
School of Materials Science and Engineering, Henan Polytechnic University, Jiaozuo 454003, China

Corresponding author: Zhang Hong-Bin, zhanghongbin2020@163.com

Funds: Project supported by the Joint Funds of the National Natural Science Foundation of China (Grant No. U1604140), the Key Science and Technology Program of Henan Province, China (Grant Nos. 172102210269, 192102210052, 212102210108, 212102210004), the Major Achievements Cultivation Project of Henan Province, China (Grant No. NSFRF170503), and the Henan Polytechnic University Innovation Team Foundation, China (Grant No. T2019-5)

文章全文 : translate this paragraph

参考文献

[1]	Wu Q X, Wang X K, Lin H, Xia M H 2020 Mech. Syst. Signal Process. 144 106968 Google Scholar
[2]	Ouyang H M, Tian Z, Yu L L, Zhang G M 2020 J. Frankl. Inst. 357 8299 Google Scholar
[3]	Lin B T, Zhang Q W, Fan F, Shen S Z 2020 Appl. Math. Model. 87 606 Google Scholar
[4]	Wu S T 2009 J. Sound Vib. 323 1 Google Scholar
[5]	王观, 胡华, 伍康, 李刚, 王力军 2016 65 200702 Google Scholar Wang G, Hu H, Wu K, Li G, Wang L J 2016 Acta Phys. Sin. 65 200702 Google Scholar
[6]	Matthews M R 1989 Res. Sci. Educ. 19 187 Google Scholar
[7]	Czolczynski K, Perlikowski P, Stefanski A, Kapitaniak T 2009 Physica A 388 5013 Google Scholar
[8]	Szumiński W, Woźniak D 2020 Commun. Nonlinear Sci. Numer. Simulat. 83 105099 Google Scholar
[9]	Náprstek J, Fischer C 2013 Comput. Struct. 124 74 Google Scholar
[10]	Han N, Cao Q J 2017 Int. J. Mech. Sci. 127 91 Google Scholar
[11]	Amer T S, Bek M A, Abohamer M K 2019 Mech. Res. Commun. 95 23 Google Scholar
[12]	方潘, 侯勇俊, 张丽萍, 杜明俊, 张梦媛 2016 65 014501 Google Scholar Fang P, Hou Y J, Zhang L P, Du M J, Zhang M Y 2016 Acta Phys. Sin. 65 014501 Google Scholar
[13]	Kapitaniak M, Perlikowski P, Kapitaniak T 2013 Commun. Nonlinear Sci. Numer. Simulat. 18 2088 Google Scholar
[14]	萧寒, 唐驾时, 梁翠香 2009 58 2989 Google Scholar Xiao H, Tang J S, Liang C X 2009 Acta Phys. Sin. 58 2989 Google Scholar
[15]	张利娟, 张华彪, 李欣业 2018 67 244302 Google Scholar Zhang L J, Zhang H B, Li X Y 2018 Acta Phys. Sin. 67 244302 Google Scholar
[16]	Bek M A, Amer T S, Sirwah M A, Awrejcewicz J, Arab A A 2020 Results Phys. 19 103465 Google Scholar
[17]	Butikov E I 2015 Commun. Nonlinear Sci. Numer. Simulat. 20 298 Google Scholar
[18]	Zhou L Q, Liu S S, Chen F Q 2017 Chaos Solit. Fract. 99 270 Google Scholar
[19]	Franco E, Astolfi A, Baena F R 2018 Mech. Mach. Theory 130 539 Google Scholar
[20]	Najdecka A, Kapitaniak T, Wiercigroch M 2015 Int. J. Non-Linear Mech. 70 84 Google Scholar
[21]	Stefanski A, Pikunov D, Balcerzak M, Dabrowski A 2020 Int. J. Mech. Sci. 173 105454 Google Scholar
[22]	Wijata A, Polczyński K, Awrejcewicz J 2021 Mech. Syst. Signal Process. 150 107229 Google Scholar
[23]	Kholostova O V 1995 J. Appl. Maths. Mechs. 59 553 Google Scholar
[24]	Jallouli A, Kacem N, Bouhaddi N. 2017 Commun. Nonlinear Sci. Numer. Simulat. 42 1 Google Scholar
[25]	Brzeski P, Perlikowski P, Yanchuk S, Kapitaniak T 2012 J. Sound Vib. 331 5347 Google Scholar
[26]	Witz J A 1995 Ocean Eng. 22 411 Google Scholar
[27]	Peláez J, Andrés Y N 2005 J. Guid. Control Dynam. 28 611 Google Scholar
[28]	Li Y S, Yang M M, Sun H X, Liu Z M, Zhang Y 2018 J. Intell. Robot. Syst. 89 485 Google Scholar
[29]	Zheng Y J, Shen G X, Li Y G, Li M, Liu H M 2014 J. Iron Steel Res. Int. 21 837 Google Scholar
[30]	Kojima H, Fukatsu K, Trivailo P M 2015 Acta Astronaut. 106 24 Google Scholar
[31]	Shen G X, Li M 2009 J. Mater. Process. Tech. 209 5002 Google Scholar
[32]	Nayfeh A H 1983 J. Sound Vib. 88 1 Google Scholar
[33]	Golubitsky M, Schaeffer D G 1985 Singularities and Groups in Bifurcation Theory (Vol. Ⅰ) (New York: Springer-Verlag) pp131−133

施引文献

图 1 受垂直激励和水平约束的单摆模型

Fig. 1. Simple pendulum model with vertical excitation and horizontal constraint.

下载: 全尺寸图片幻灯片

图 2 σ变化下改变b的幅频响应曲线

Fig. 2. Amplitude-frequency response curves with different σ and b.

下载: 全尺寸图片幻灯片

图 3 σ变化下改变k₃₃的幅频响应曲线

Fig. 3. Amplitude-frequency response curves with different σ and k_33.

下载: 全尺寸图片幻灯片

图 4 σ变化下改变c₁₁的幅频响应曲线

Fig. 4. Amplitude-frequency response curves with different σ and c₁₁.

下载: 全尺寸图片幻灯片

图 5 c₁₁变化下改变σ的幅频响应曲线

Fig. 5. Amplitude-frequency response curves with different c₁₁ and σ.

下载: 全尺寸图片幻灯片

图 6 k₃₃变化下改变σ的幅频响应曲线

Fig. 6. Amplitude-frequency response curves with different k₃₃ and σ.

下载: 全尺寸图片幻灯片

图 7 受垂直激励和水平约束单摆系统1/2次亚谐共振分岔拓扑结构

Fig. 7. Bifurcation topology of 1/2-order subharmonic resonance of a simple pendulum system with vertical excitation and horizontal constraint.

下载: 全尺寸图片幻灯片

图 8 (a)势阱曲线; (b), (c)相轨线及其局部放大图

Fig. 8. (a) Potential well curve; (b), (c) phase track and its enlarged view.

下载: 全尺寸图片幻灯片

图 9 系统混沌运动的参数条件

Fig. 9. Parameter conditions for chaotic motion of the system

下载: 全尺寸图片幻灯片

图 10 单摆系统亚谐共振在ω_b = 2时的混沌吸引子

Fig. 10. Chaotic attractor of simple pendulum system when ω_b = 2.

下载: 全尺寸图片幻灯片

图 11 摆长l变化下的分岔图

Fig. 11. Bifurcation diagram with different l.

下载: 全尺寸图片幻灯片

图 12 ω_b变化下的(a)分岔和(b)最大Lyapunov指数

Fig. 12. (a) Bifurcation and (b) maximum Lyapunov exponent with different ω_b.

下载: 全尺寸图片幻灯片

图 13 ω_b变化下的(a)−(c)相图和(d)−(f)时间历程图　(a), (d) ω_b = 0.5; (b), (e) ω_b = 1.02; (c), (f) ω_b = 1.8

Fig. 13. (a)−(c) Phase diagram and (d)−(f) time history diagram with different ω_b : (a), (d) ω_b = 0.5; (b), (e) ω_b = 1.02; (c), (f) ω_b = 1.8

下载: 全尺寸图片幻灯片

图 14 当ω_b = 1.8时b变化下的时间历程图　(a) b = 0.28; (b) b = 0.38; (c) b = 0.58

Fig. 14. Time history diagram when b changes and ω_b = 1.8: (a) b = 0.28; (b) b = 0.38; (c) b = 0.58.

下载: 全尺寸图片幻灯片

图 15 c₁₁变化下的(a)分岔和(b)最大Lyapunov指数

Fig. 15. (a) Bifurcation and (b) maximum Lyapunov exponent with different c₁₁.

下载: 全尺寸图片幻灯片

图 16 c₁₁变化下的(a)−(c)相图和(d)−(f)时间历程图　(a), (d) c₁₁ = 0.6; (b), (e) c₁₁ = 0.63; (c), (f) c₁₁ = 1.2

Fig. 16. (a)−(c) Phase diagram and (d)−(f) time history diagram with different c₁₁: (a), (d) c₁₁ = 0.6; (b), (e) c₁₁ = 0.63; (c), (f) c₁₁ = 1.2.

下载: 全尺寸图片幻灯片

图 17 g₁变化下的(a)分岔和(b)最大Lyapunov指数

Fig. 17. (a) Bifurcation and (b) maximum Lyapunov exponent with different g₁.

下载: 全尺寸图片幻灯片

图 18 g₁变化下的(a)−(c)相图和(d)−(f)时间历程图　(a), (d) g₁ = 0.27; (b), (e) g₁ = 0.28; (c), (f) g₁ = 0.36

Fig. 18. (a)−(c) Phase diagram and (d)−(f) time history diagram with different g₁: (a), (d) g₁ = 0.27; (b), (e) g₁ = 0.28; (c), (f) g₁ = 0.36.

下载: 全尺寸图片幻灯片

图 19 k₃₃变化下的(a)分岔和(b)最大Lyapunov指数

Fig. 19. (a) Bifurcation and (b) maximum Lyapunov exponent with different k_33..

下载: 全尺寸图片幻灯片

图 20 k₃₃变化下的(a)−(c)相图和(d)−(f)时间历程图　(a), (d) k₃₃ = 0.6; (b), (e) k₃₃ = 1.2; (c), (f) k₃₃ = 1.4

Fig. 20. (a)−(c) Phase diagram and (d)−(f) time history diagram with different k₃₃: (a), (d) k₃₃ = 0.6; (b), (e) k₃₃ = 1.2; (c), (f) k₃₃ = 1.4

下载: 全尺寸图片幻灯片

图 21 b变化下的(a)分岔和(b)最大Lyapunov指数

Fig. 21. (a) Bifurcation and (b) maximum Lyapunov exponent with different b.

下载: 全尺寸图片幻灯片

图 22 b变化下的(a)−(c)相图和(d)−(f)时间历程图　(a), (d) b = 0.19; (b), (e) b = 0.28; (c), (f) b = 0.36

Fig. 22. (a)−(c) Phase diagram and (d)−(f) time history diagram with different b: (a), (d) b = 0.19; (b), (e) b = 0.28; (c), (f) b = 0.36

下载: 全尺寸图片幻灯片

图 23 当b = 0.36时ω_b变化下的时间历程图　(a) ω_b = 1.3 (b) ω_b = 1.5; (c) ω_b = 1.7

Fig. 23. Time history diagram when ω_b changes and b = 0.36: (a) ω_b = 1.3; (b) ω_b = 1.5; (c) ω_b = 1.7.

下载: 全尺寸图片幻灯片

图 24 单摆非线性系统在双参数域上的运动　(a) ω_b-c₁₁; (b) c₁₁-k₃₃; (c) k₃₃-g₁; (d) g₁-b; (e) b-ω_b

Fig. 24. Motion of a simple pendulum nonlinear system in the bi-parameter domain: (a) ω_b-c₁₁; (b) c₁₁-k₃₃; (c) k₃₃-g₁; (d) g₁-b; (e) b-ω_b

下载: 全尺寸图片幻灯片

图 25 系统在参数b变化时的吸引子、吸引域　(a) b = 0.11; (b) b = 0.23; (c) b = 0.32; (d) b = 0.35; (e) b = 0.49; (f) b = 0.81

Fig. 25. Attractor and attraction domain of the system when the parameter b changes: (a) b = 0.11; (b) b = 0.23; (c) b = 0.32; (d) b = 0.35; (e) b = 0.49; (f) b = 0.81.

下载: 全尺寸图片幻灯片

map

[1]	Wu Q X, Wang X K, Lin H, Xia M H 2020 Mech. Syst. Signal Process. 144 106968 Google Scholar
[2]	Ouyang H M, Tian Z, Yu L L, Zhang G M 2020 J. Frankl. Inst. 357 8299 Google Scholar
[3]	Lin B T, Zhang Q W, Fan F, Shen S Z 2020 Appl. Math. Model. 87 606 Google Scholar
[4]	Wu S T 2009 J. Sound Vib. 323 1 Google Scholar
[5]	王观, 胡华, 伍康, 李刚, 王力军 2016 65 200702 Google Scholar Wang G, Hu H, Wu K, Li G, Wang L J 2016 Acta Phys. Sin. 65 200702 Google Scholar
[6]	Matthews M R 1989 Res. Sci. Educ. 19 187 Google Scholar
[7]	Czolczynski K, Perlikowski P, Stefanski A, Kapitaniak T 2009 Physica A 388 5013 Google Scholar
[8]	Szumiński W, Woźniak D 2020 Commun. Nonlinear Sci. Numer. Simulat. 83 105099 Google Scholar
[9]	Náprstek J, Fischer C 2013 Comput. Struct. 124 74 Google Scholar
[10]	Han N, Cao Q J 2017 Int. J. Mech. Sci. 127 91 Google Scholar
[11]	Amer T S, Bek M A, Abohamer M K 2019 Mech. Res. Commun. 95 23 Google Scholar
[12]	方潘, 侯勇俊, 张丽萍, 杜明俊, 张梦媛 2016 65 014501 Google Scholar Fang P, Hou Y J, Zhang L P, Du M J, Zhang M Y 2016 Acta Phys. Sin. 65 014501 Google Scholar
[13]	Kapitaniak M, Perlikowski P, Kapitaniak T 2013 Commun. Nonlinear Sci. Numer. Simulat. 18 2088 Google Scholar
[14]	萧寒, 唐驾时, 梁翠香 2009 58 2989 Google Scholar Xiao H, Tang J S, Liang C X 2009 Acta Phys. Sin. 58 2989 Google Scholar
[15]	张利娟, 张华彪, 李欣业 2018 67 244302 Google Scholar Zhang L J, Zhang H B, Li X Y 2018 Acta Phys. Sin. 67 244302 Google Scholar
[16]	Bek M A, Amer T S, Sirwah M A, Awrejcewicz J, Arab A A 2020 Results Phys. 19 103465 Google Scholar
[17]	Butikov E I 2015 Commun. Nonlinear Sci. Numer. Simulat. 20 298 Google Scholar
[18]	Zhou L Q, Liu S S, Chen F Q 2017 Chaos Solit. Fract. 99 270 Google Scholar
[19]	Franco E, Astolfi A, Baena F R 2018 Mech. Mach. Theory 130 539 Google Scholar
[20]	Najdecka A, Kapitaniak T, Wiercigroch M 2015 Int. J. Non-Linear Mech. 70 84 Google Scholar
[21]	Stefanski A, Pikunov D, Balcerzak M, Dabrowski A 2020 Int. J. Mech. Sci. 173 105454 Google Scholar
[22]	Wijata A, Polczyński K, Awrejcewicz J 2021 Mech. Syst. Signal Process. 150 107229 Google Scholar
[23]	Kholostova O V 1995 J. Appl. Maths. Mechs. 59 553 Google Scholar
[24]	Jallouli A, Kacem N, Bouhaddi N. 2017 Commun. Nonlinear Sci. Numer. Simulat. 42 1 Google Scholar
[25]	Brzeski P, Perlikowski P, Yanchuk S, Kapitaniak T 2012 J. Sound Vib. 331 5347 Google Scholar
[26]	Witz J A 1995 Ocean Eng. 22 411 Google Scholar
[27]	Peláez J, Andrés Y N 2005 J. Guid. Control Dynam. 28 611 Google Scholar
[28]	Li Y S, Yang M M, Sun H X, Liu Z M, Zhang Y 2018 J. Intell. Robot. Syst. 89 485 Google Scholar
[29]	Zheng Y J, Shen G X, Li Y G, Li M, Liu H M 2014 J. Iron Steel Res. Int. 21 837 Google Scholar
[30]	Kojima H, Fukatsu K, Trivailo P M 2015 Acta Astronaut. 106 24 Google Scholar
[31]	Shen G X, Li M 2009 J. Mater. Process. Tech. 209 5002 Google Scholar
[32]	Nayfeh A H 1983 J. Sound Vib. 88 1 Google Scholar
[33]	Golubitsky M, Schaeffer D G 1985 Singularities and Groups in Bifurcation Theory (Vol. Ⅰ) (New York: Springer-Verlag) pp131−133

[1]	刘洪臣, 苏振霞. 双降压式全桥逆变器非线性现象的研究. , 2014, 63(1): 010505. doi: 10.7498/aps.63.010505
[2]	王斌, 薛建议, 贺好艳, 朱德兰. 基于线性矩阵不等式的一类新羽翼倍增混沌分析与控制. , 2014, 63(21): 210502. doi: 10.7498/aps.63.210502
[3]	刘洪臣, 李飞, 杨爽. 基于周期性扩频的单相H桥逆变器非线性现象的研究. , 2013, 62(11): 110504. doi: 10.7498/aps.62.110504
[4]	张方樱, 杨汝, 龙晓莉, 谢陈跃, 陈虹. V2控制Buck变换器分岔与混沌行为的机理及镇定. , 2013, 62(21): 218404. doi: 10.7498/aps.62.218404
[5]	丁虎, 严巧赟, 陈立群. 轴向加速运动黏弹性梁受迫振动中的混沌动力学. , 2013, 62(20): 200502. doi: 10.7498/aps.62.200502
[6]	孟宗, 付立元, 宋明厚. 一类非线性相对转动系统的组合谐波分岔行为研究. , 2013, 62(5): 054501. doi: 10.7498/aps.62.054501
[7]	刘洪臣, 王云, 苏振霞. 单相三电平H桥逆变器分岔现象的研究. , 2013, 62(24): 240506. doi: 10.7498/aps.62.240506
[8]	胡文, 赵广浩, 张弓, 张景乔, 刘贤龙. 时标正弦动力学方程稳定性与分岔分析. , 2012, 61(17): 170505. doi: 10.7498/aps.61.170505
[9]	李海滨, 王博华, 张志强, 刘爽, 李延树. 一类非线性相对转动系统的组合共振分岔与混沌. , 2012, 61(9): 094501. doi: 10.7498/aps.61.094501
[10]	古华光, 朱洲, 贾冰. 一类新的混沌神经放电的动力学特征的实验和数学模型研究. , 2011, 60(10): 100505. doi: 10.7498/aps.60.100505
[11]	陈章耀, 毕勤胜. Jerk系统耦合的分岔和混沌行为. , 2010, 59(11): 7669-7678. doi: 10.7498/aps.59.7669
[12]	张晓芳, 陈章耀, 毕勤胜. 非线性电路通向混沌的演化过程. , 2010, 59(5): 3057-3065. doi: 10.7498/aps.59.3057
[13]	张晓芳, 陈章耀, 毕勤胜. 耦合电路中的复杂振荡行为分析. , 2009, 58(5): 2963-2970. doi: 10.7498/aps.58.2963
[14]	邹建龙, 马西奎. 一类由饱和引起的非线性现象. , 2008, 57(2): 720-725. doi: 10.7498/aps.57.720
[15]	于万波, 魏小鹏. 一个小波函数指数参数变化的分岔现象. , 2006, 55(8): 3969-3973. doi: 10.7498/aps.55.3969
[16]	张维, 周淑华, 任勇, 山秀明. Turbo译码算法的分岔与控制. , 2006, 55(2): 622-627. doi: 10.7498/aps.55.622
[17]	马西奎, 杨梅, 邹建龙, 王玲桃. 一种时延范德波尔电磁系统中的复杂行为(Ⅰ)——分岔与混沌现象. , 2006, 55(11): 5648-5656. doi: 10.7498/aps.55.5648
[18]	李　明, 马西奎, 戴　栋, 张　浩. 基于符号序列描述的一类分段光滑系统中分岔现象与混沌分析. , 2005, 54(3): 1084-1091. doi: 10.7498/aps.54.1084
[19]	罗晓曙, 汪秉宏, 陈关荣, 全宏俊, 方锦清, 邹艳丽, 蒋品群. DC-DC buck变换器的分岔行为及混沌控制研究. , 2003, 52(1): 12-17. doi: 10.7498/aps.52.12
[20]	郝建红, 丁武. 行波管放大器中辐射场的极限环振荡和混沌. , 2003, 52(4): 906-910. doi: 10.7498/aps.52.906

计量

文章访问数: 6019
PDF下载量: 142
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

受垂直激励和水平约束的单摆系统亚谐共振分岔与混沌