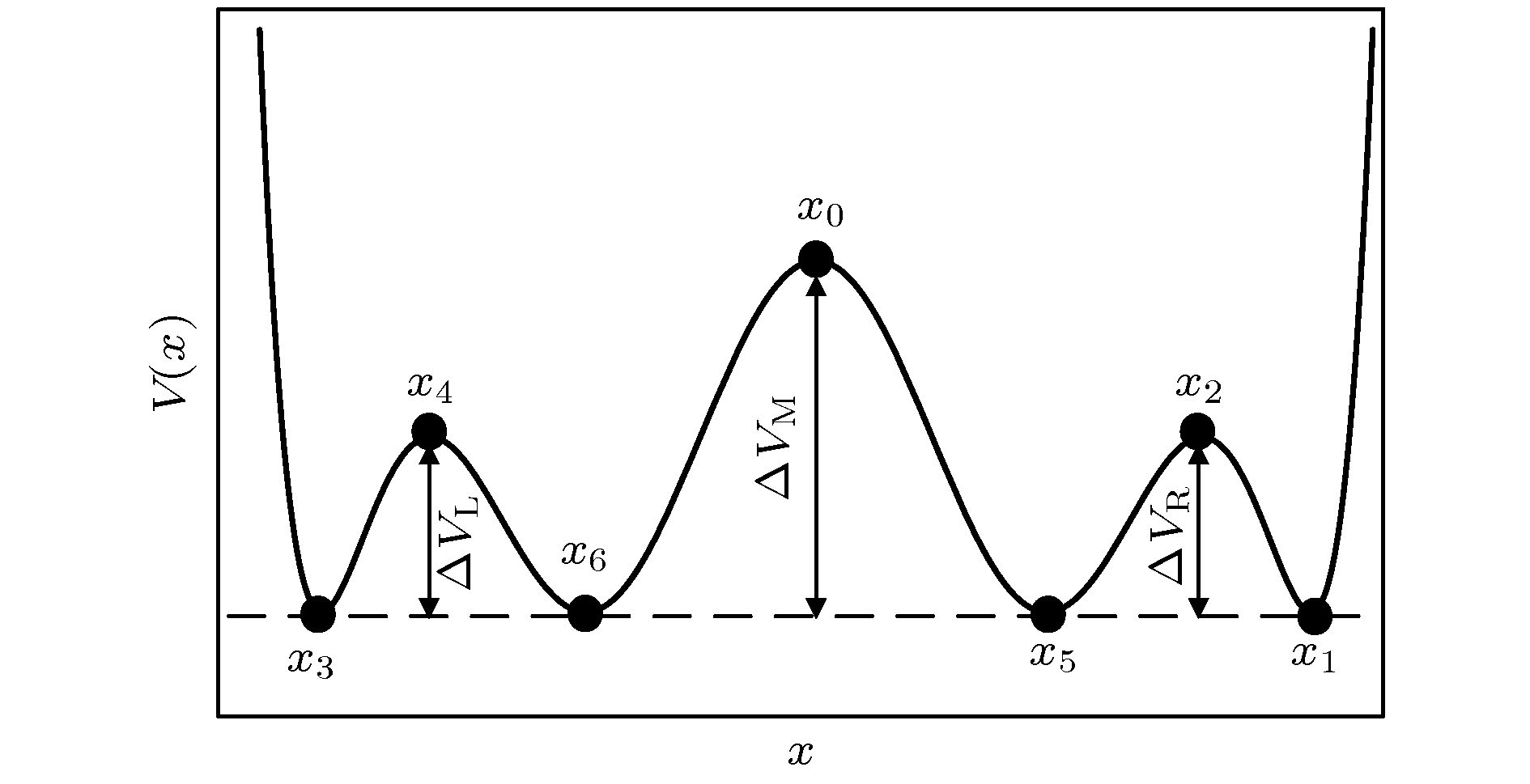
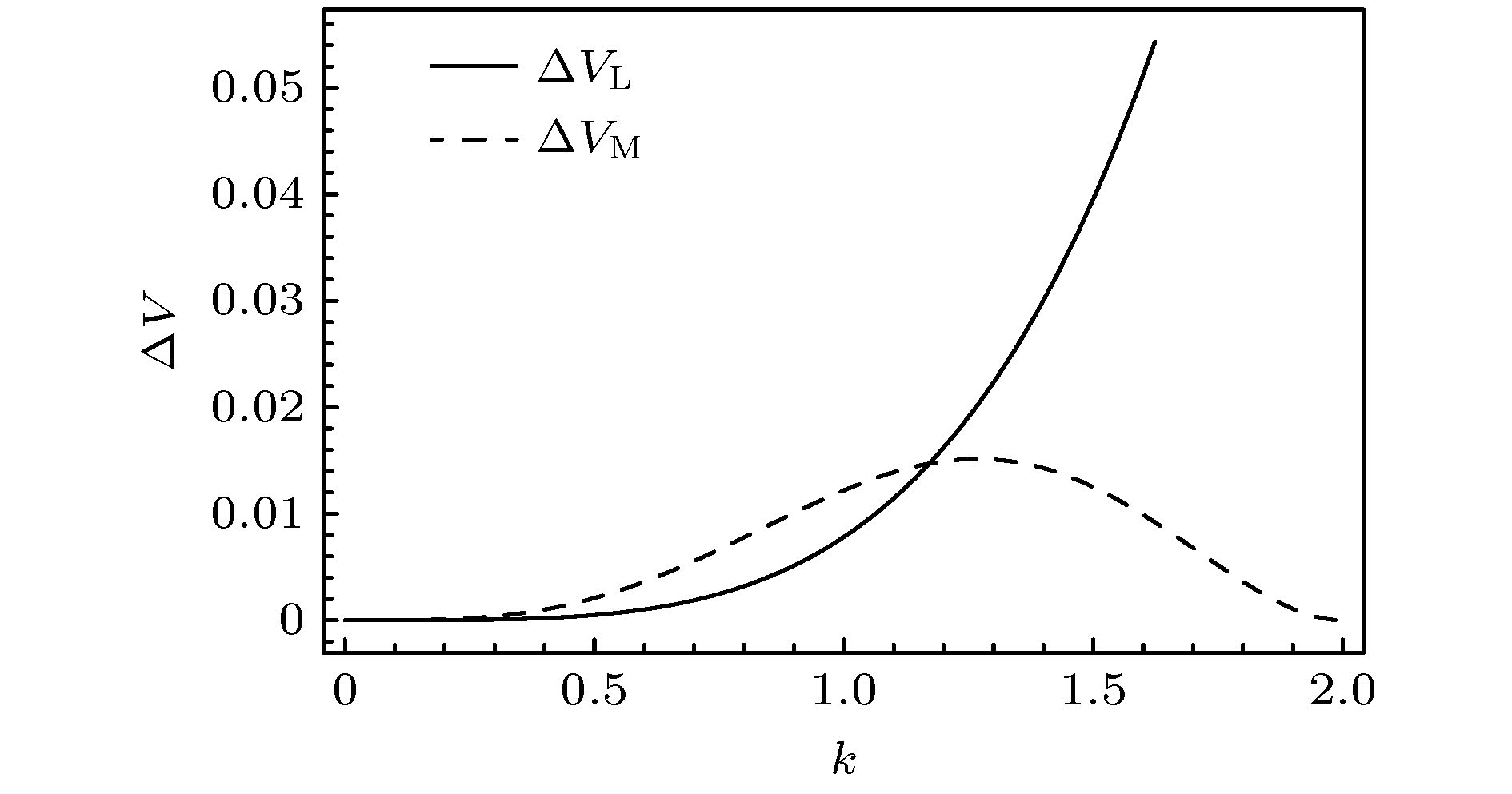
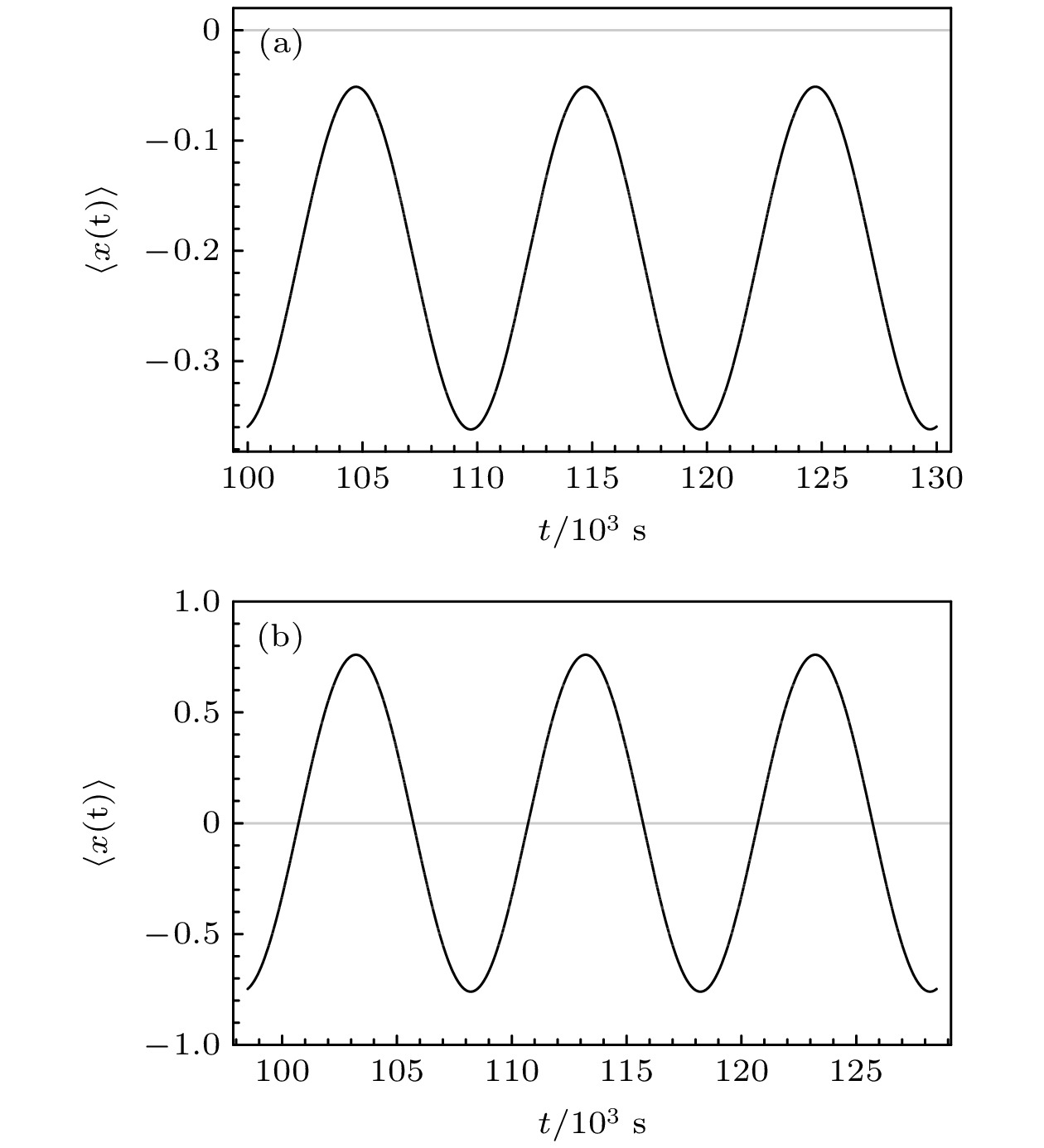
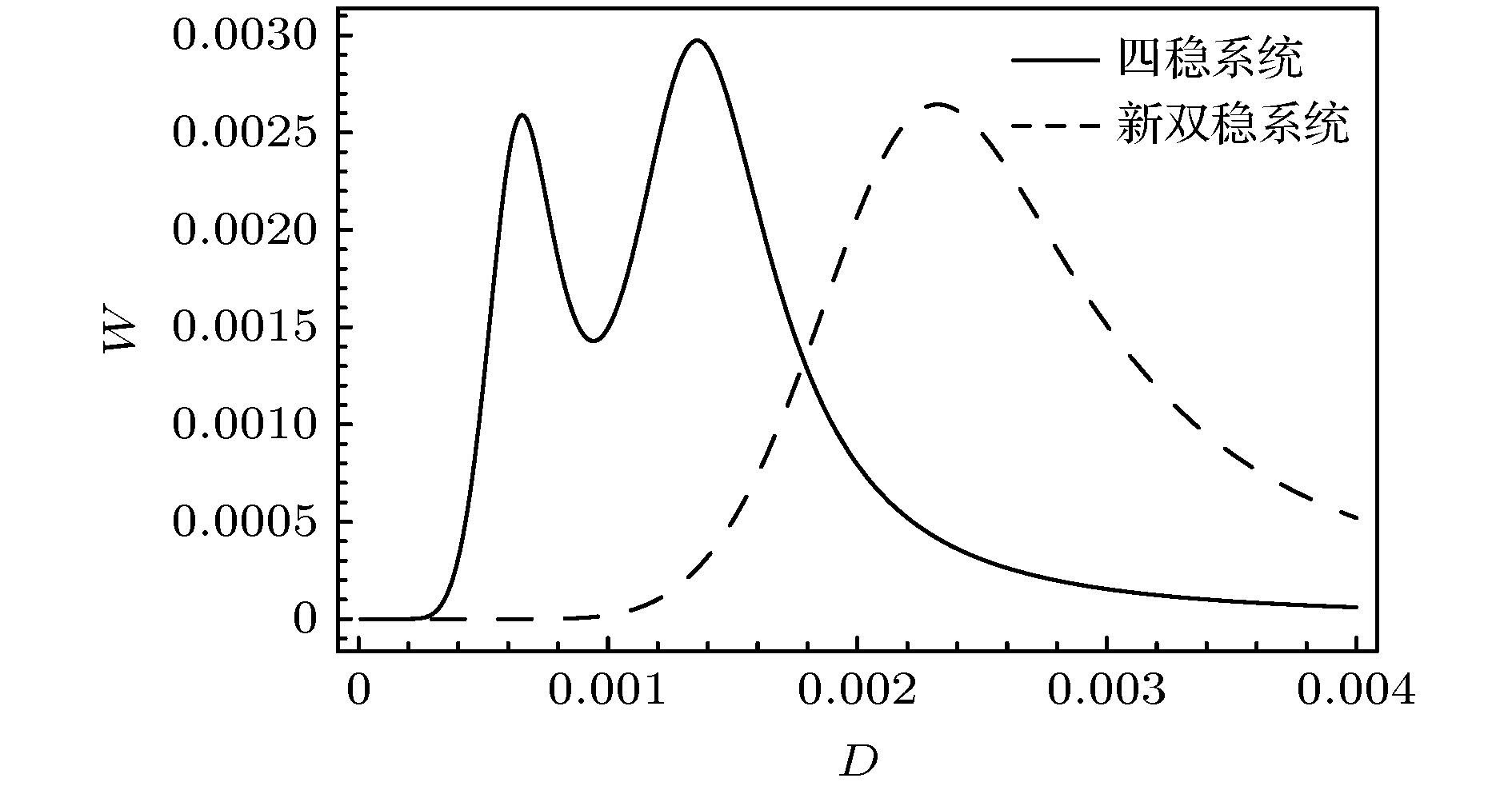
-
In this paper we propose a class of 8th-order potential function, and discuss the bifurcation characteristic of such a system in detail. Then, a symmetric quad-stable system consisting of two small-scale bistable potentials on the left and right and an intermediate barrier is obtained. In order to analyze the quad-stable system characteristic effectively, under the combined action of periodic force and random force, the approximate analytical expression of the quad-stable system output response is established. Meanwhile, from the viewpoint of the energy, the work which is a process quantity is introduced to describe the capacity for work between the large-scale and small-scale bistable potential. It is found that the double stochastic resonance phenomenon does exist in the quad-stable system. The theoretical analysis and numerical simulation results indicate that when the height of the intermediate barrier is higher than the barrier height of the two small-scale bistable potentials on the left and right, as the noise intensity increases, the response of the quad-stable system transforms a small-amplitude vibration restricted in a small-scale bistable subsystem into a large-amplitude vibration across the intermediate barrier, and the work done by the periodic force presents a double-peak curve. To be more specific, as the noise intensity gradually increases from zero, the system response is first confined to a small-scale bistable potential. Under the joint action of the small-scale bistable potential, periodic force and random force, the small-scale stochastic resonance phenomenon occurs, and the first resonance peak appears. With the noise intensity increasing even further, the system response turns into the large-amplitude vibration between two small-scale bistable subsystems, resulting in the large-scale stochastic resonance phenomenon and a higher resonance peak. Thus, the work done by periodic force has the peak values at two different noise intensities, which means that the noise can induce the double stochastic resonance phenomenon in the quad-stable system. More importantly, it can be found that the small-scale stochastic resonance can enhance the effect of large-scale stochastic resonance.
[1] Benzi R, Sutera A, Vulpiani A 1981 J. Phys. A: Math. Gen. 14 L453
Google Scholar
[2] Ghosh P K, Bag B C, Ray D S 2007 Phys. Rev. E 75 032101
Google Scholar
[3] Repperger D W, Farris K A 2010 Int. J. Syst. Sci. 41 897
Google Scholar
[4] Kenmoé G D, Ngouongo Y J W, Kofané T C 2015 J. Stat. Phys. 161 475
Google Scholar
[5] Moon W, Balmforth N, Wettlaufer J S 2020 J. Phys. A: Math. Theor. 53 095001
Google Scholar
[6] Fauve S, Heslot F 1983 Phys. Lett. A 97 5
Google Scholar
[7] McNamara B, Wiesenfeld K, Roy R 1988 Phys. Rev. Lett. 60 2626
Google Scholar
[8] 王珊, 王辅忠 2018 67 160502
Google Scholar
Wang S, Wang F Z 2018 Acta Phys. Sin. 67 160502
Google Scholar
[9] Monifi F, Zhang J, Özdemir S K, Peng B, Liu Y X, Bo F, Nori F, Yang L 2016 Nat. Photonics 10 399
Google Scholar
[10] van der Groen O, Wenderoth N 2016 J. Neurosci. 36 5289
Google Scholar
[11] He G T, Min C, Tian Y 2014 Acta Phys. Pol. B 45 29
Google Scholar
[12] Liu J, Hu B, Yang F, Zang C L, Ding X J 2020 Commun. Nonlinear Sci. Numer. Simul. 85 105245
Google Scholar
[13] Moreno M V, Barci D G, Arenas Z G 2020 Phys. Rev. E 101 062110
Google Scholar
[14] Xu L, Yu T, Lai L, Zhao D Z, Deng C, Zhang L 2020 Commun. Nonlinear Sci. Numer. Simul. 83 105133
Google Scholar
[15] 林敏, 黄咏梅, 方利民 2008 57 2048
Google Scholar
Lin M, Huang Y M, Fang L M 2008 Acta Phys. Sin. 57 2048
Google Scholar
[16] 王林泽, 赵文礼, 陈旋 2012 61 160501
Google Scholar
Wang L Z, Zhao W L, Chen X 2012 Acta Phys. Sin. 61 160501
Google Scholar
[17] He L F, Cao L, Zhang G, Yi T 2018 Chin. J. Phys. 56 1588
Google Scholar
[18] Jin Y F, Xu P F 2018 14th International Federation of Automatic Control (IFAC) Workshop on Time Delay Systems (TDS) Budapest, HUNGARY, JUN 28-30, 2018 p189
Google Scholar
[19] Nicolis C, Nicolis G 2017 Phys. Rev. E 95 032219
Google Scholar
[20] Li J M, Chen X F, He Z J 2013 J. Sound Vib. 332 5999
Google Scholar
[21] 赖志慧, 冷永刚 2015 64 200503
Google Scholar
Lai Z H, Leng Y G 2015 Acta Phys. Sin. 64 200503
Google Scholar
[22] Bi H H, Lei Y M, Han Y Y 2019 Physica A 525 1296
Google Scholar
[23] Tang J C, Shi B Q, Li Z X, Li Y Z 2020 Chin. J. Phys. 66 50
Google Scholar
[24] Vilar J M G, Rubi J M 1997 Phys. Rev. Lett. 78 2882
Google Scholar
[25] Alfonsi L, Gammaitoni L, Santucci S, Bulsara A 2000 Phys. Rev. E 62 299
Google Scholar
[26] 张晓燕, 徐伟, 周丙常 2011 60 060514
Google Scholar
Zhang X Y, Xu W, Zhou B C 2011 Acta Phys. Sin. 60 060514
Google Scholar
[27] Zhang X Y, Zheng X Y 2019 Indian J. Phys. 93 1051
Google Scholar
[28] Iwai T 2001 J. Phys. Soc. Jpn. 70 353
Google Scholar
[29] Iwai T 2001 Physica A 300 350
Google Scholar
[30] McNamara B, Wiesenfeld K 1989 Phys. Rev. A 39 4854
Google Scholar
-
图 1 非线性系统(5)的分岔图
Figure 1. The bifurcation diagram corresponding to the system(5).
图 2 四稳势函数曲线
Figure 2. The potential function curve of the quad-stable system.
图 3 势垒高度
$\Delta V$ 随参数$k$ 的变化(实线: 左势垒高度$\Delta {V_{\rm{L}}}$ ; 虚线: 中间势垒高度$\Delta {V_{\rm{M}}}$ )Figure 3. The relational curve of
$\Delta V$ vs$k$ (solid line: height of the left barrier$\Delta {V_{\rm{L}}}$ ; dotted line: height of the intermediate barrier$\Delta {V_{\rm{M}}}$ ).
图 4 系统输出响应的近似理论曲线 (a)
$D = 0.0005$ ; (b)$D = 0.0015$ Figure 4. The approximate theoretical curve of system output response: (a)
$D = 0.0005$ ; (b)$D = 0.0015$ .
图 5 功
$W$ 与噪声强度$D$ 之间关系的近似理论曲线Figure 5. The approximate theoretical relational curve of
$W$ vs$D$ .
图 6 势函数曲线(实线: 新双稳系统; 虚线: 四稳系统)
Figure 6. The potential function curve(solid line: new bistable system; dotted line: quad-stable system).
图 7 功
$W$ 随噪声强度$D$ 变化的近似理论曲线(实线: 四稳系统; 虚线: 新双稳系统)Figure 7. The approximate theoretical relational curve of
$W$ vs$D$ (solid line: quad-stable system; dotted line: new bistable system).
图 8 功
$W$ 随噪声强度$D$ 变化的仿真曲线Figure 8. The relational curve of
$W$ vs$D$ .
图 9 输出信号波形 (a)
$D = 0.0016$ ; (b)$D = 0.0048$ Figure 9. The waveform of the output signal: (a)
$D = 0.0016$ ; (b)$D = 0.0048$ .表 1 系统结构与参数
$k$ 的关系Table 1. The relationship between potential structure form and parameter
$k$ .系统结构 $0 < k < 2$ $2 < k < 4$ $4 < k < 6$ 稳定不动点个数 4 3 2 $V\left( {x, k} \right)$的结构类型 四稳系统 三稳系统 双稳系统 
DownLoad: CSV
-
[1] Benzi R, Sutera A, Vulpiani A 1981 J. Phys. A: Math. Gen. 14 L453
Google Scholar
[2] Ghosh P K, Bag B C, Ray D S 2007 Phys. Rev. E 75 032101
Google Scholar
[3] Repperger D W, Farris K A 2010 Int. J. Syst. Sci. 41 897
Google Scholar
[4] Kenmoé G D, Ngouongo Y J W, Kofané T C 2015 J. Stat. Phys. 161 475
Google Scholar
[5] Moon W, Balmforth N, Wettlaufer J S 2020 J. Phys. A: Math. Theor. 53 095001
Google Scholar
[6] Fauve S, Heslot F 1983 Phys. Lett. A 97 5
Google Scholar
[7] McNamara B, Wiesenfeld K, Roy R 1988 Phys. Rev. Lett. 60 2626
Google Scholar
[8] 王珊, 王辅忠 2018 67 160502
Google Scholar
Wang S, Wang F Z 2018 Acta Phys. Sin. 67 160502
Google Scholar
[9] Monifi F, Zhang J, Özdemir S K, Peng B, Liu Y X, Bo F, Nori F, Yang L 2016 Nat. Photonics 10 399
Google Scholar
[10] van der Groen O, Wenderoth N 2016 J. Neurosci. 36 5289
Google Scholar
[11] He G T, Min C, Tian Y 2014 Acta Phys. Pol. B 45 29
Google Scholar
[12] Liu J, Hu B, Yang F, Zang C L, Ding X J 2020 Commun. Nonlinear Sci. Numer. Simul. 85 105245
Google Scholar
[13] Moreno M V, Barci D G, Arenas Z G 2020 Phys. Rev. E 101 062110
Google Scholar
[14] Xu L, Yu T, Lai L, Zhao D Z, Deng C, Zhang L 2020 Commun. Nonlinear Sci. Numer. Simul. 83 105133
Google Scholar
[15] 林敏, 黄咏梅, 方利民 2008 57 2048
Google Scholar
Lin M, Huang Y M, Fang L M 2008 Acta Phys. Sin. 57 2048
Google Scholar
[16] 王林泽, 赵文礼, 陈旋 2012 61 160501
Google Scholar
Wang L Z, Zhao W L, Chen X 2012 Acta Phys. Sin. 61 160501
Google Scholar
[17] He L F, Cao L, Zhang G, Yi T 2018 Chin. J. Phys. 56 1588
Google Scholar
[18] Jin Y F, Xu P F 2018 14th International Federation of Automatic Control (IFAC) Workshop on Time Delay Systems (TDS) Budapest, HUNGARY, JUN 28-30, 2018 p189
Google Scholar
[19] Nicolis C, Nicolis G 2017 Phys. Rev. E 95 032219
Google Scholar
[20] Li J M, Chen X F, He Z J 2013 J. Sound Vib. 332 5999
Google Scholar
[21] 赖志慧, 冷永刚 2015 64 200503
Google Scholar
Lai Z H, Leng Y G 2015 Acta Phys. Sin. 64 200503
Google Scholar
[22] Bi H H, Lei Y M, Han Y Y 2019 Physica A 525 1296
Google Scholar
[23] Tang J C, Shi B Q, Li Z X, Li Y Z 2020 Chin. J. Phys. 66 50
Google Scholar
[24] Vilar J M G, Rubi J M 1997 Phys. Rev. Lett. 78 2882
Google Scholar
[25] Alfonsi L, Gammaitoni L, Santucci S, Bulsara A 2000 Phys. Rev. E 62 299
Google Scholar
[26] 张晓燕, 徐伟, 周丙常 2011 60 060514
Google Scholar
Zhang X Y, Xu W, Zhou B C 2011 Acta Phys. Sin. 60 060514
Google Scholar
[27] Zhang X Y, Zheng X Y 2019 Indian J. Phys. 93 1051
Google Scholar
[28] Iwai T 2001 J. Phys. Soc. Jpn. 70 353
Google Scholar
[29] Iwai T 2001 Physica A 300 350
Google Scholar
[30] McNamara B, Wiesenfeld K 1989 Phys. Rev. A 39 4854
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5274
- PDF Downloads: 116
- Cited By: 0
