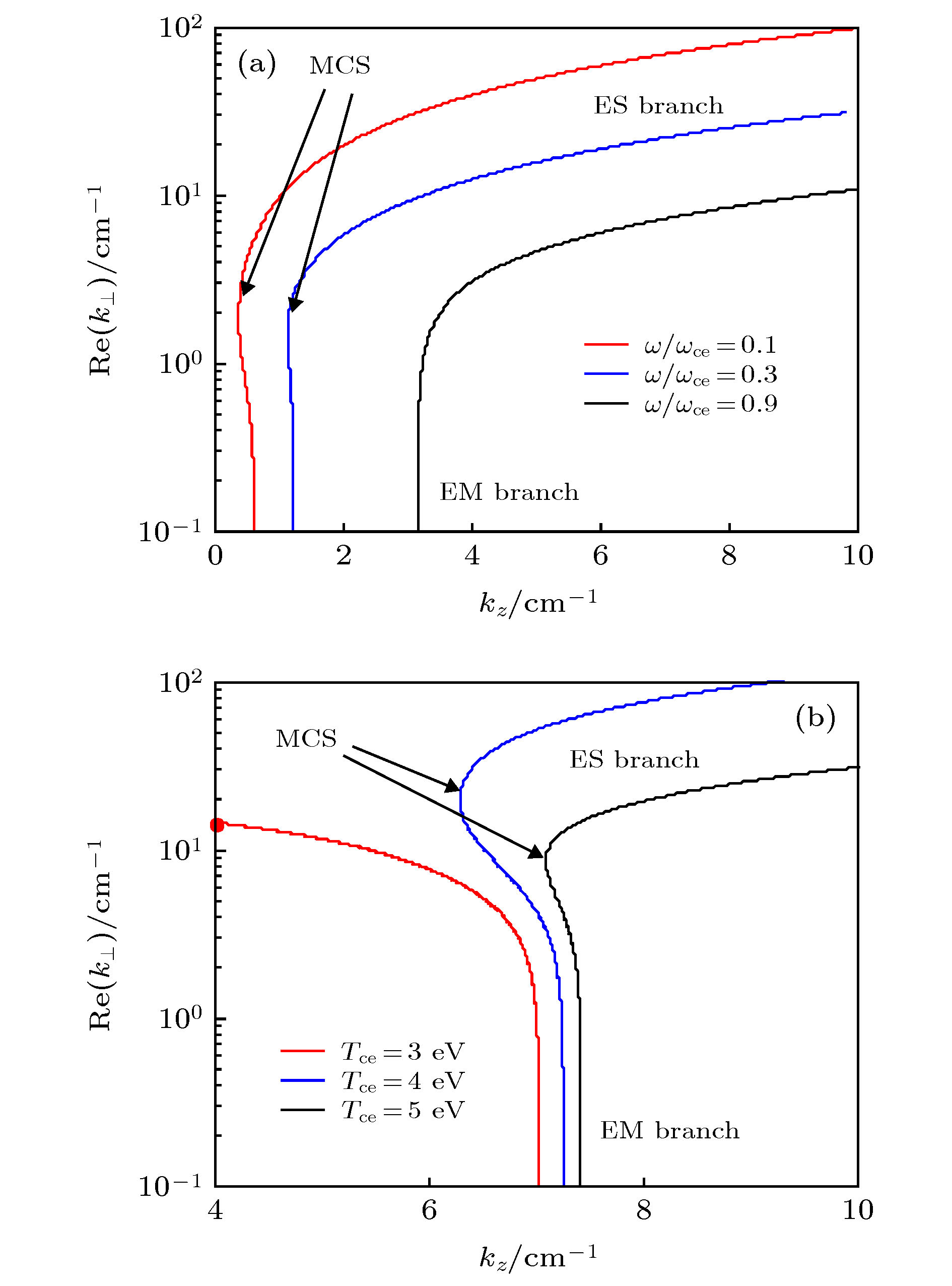
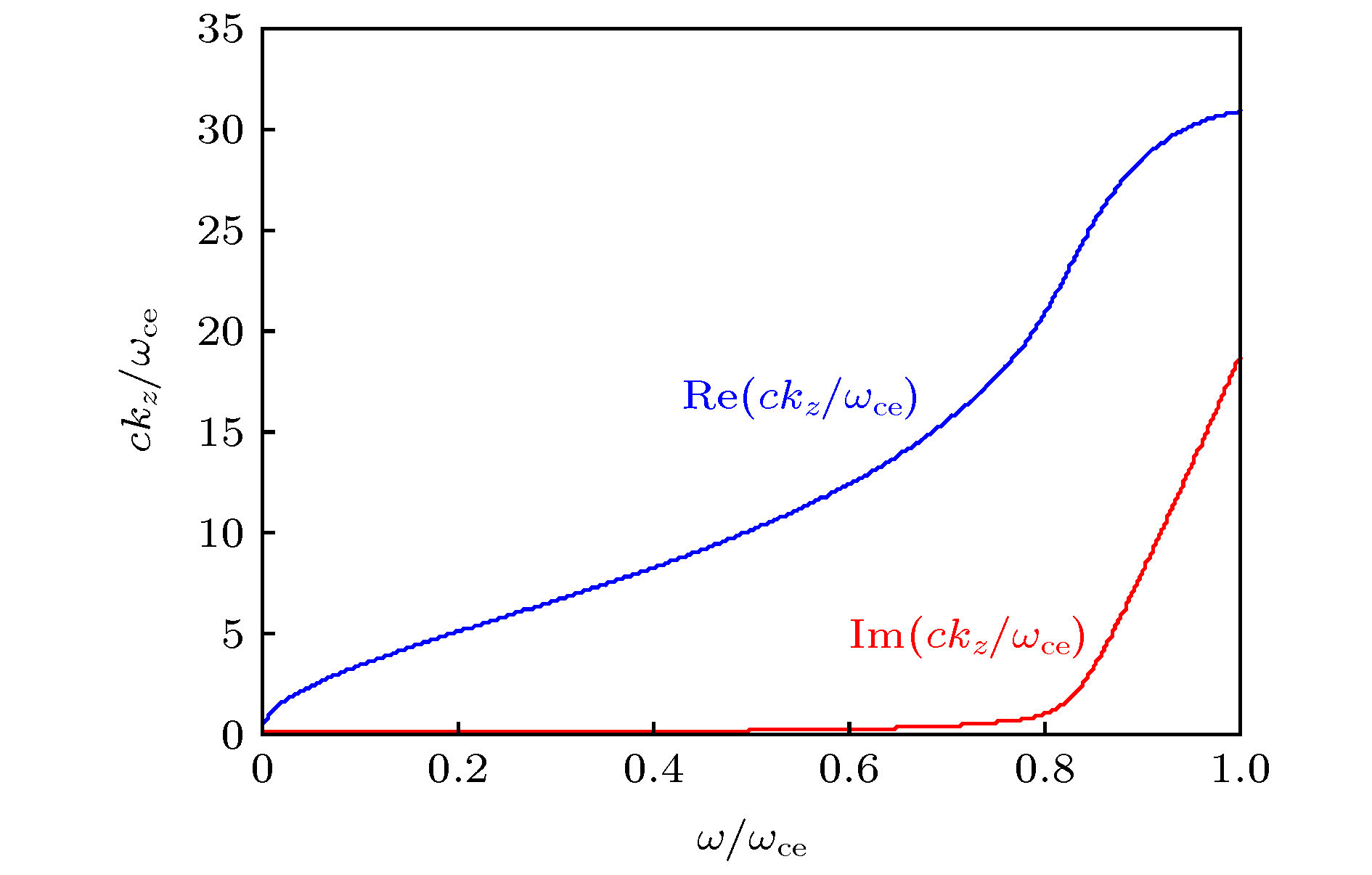
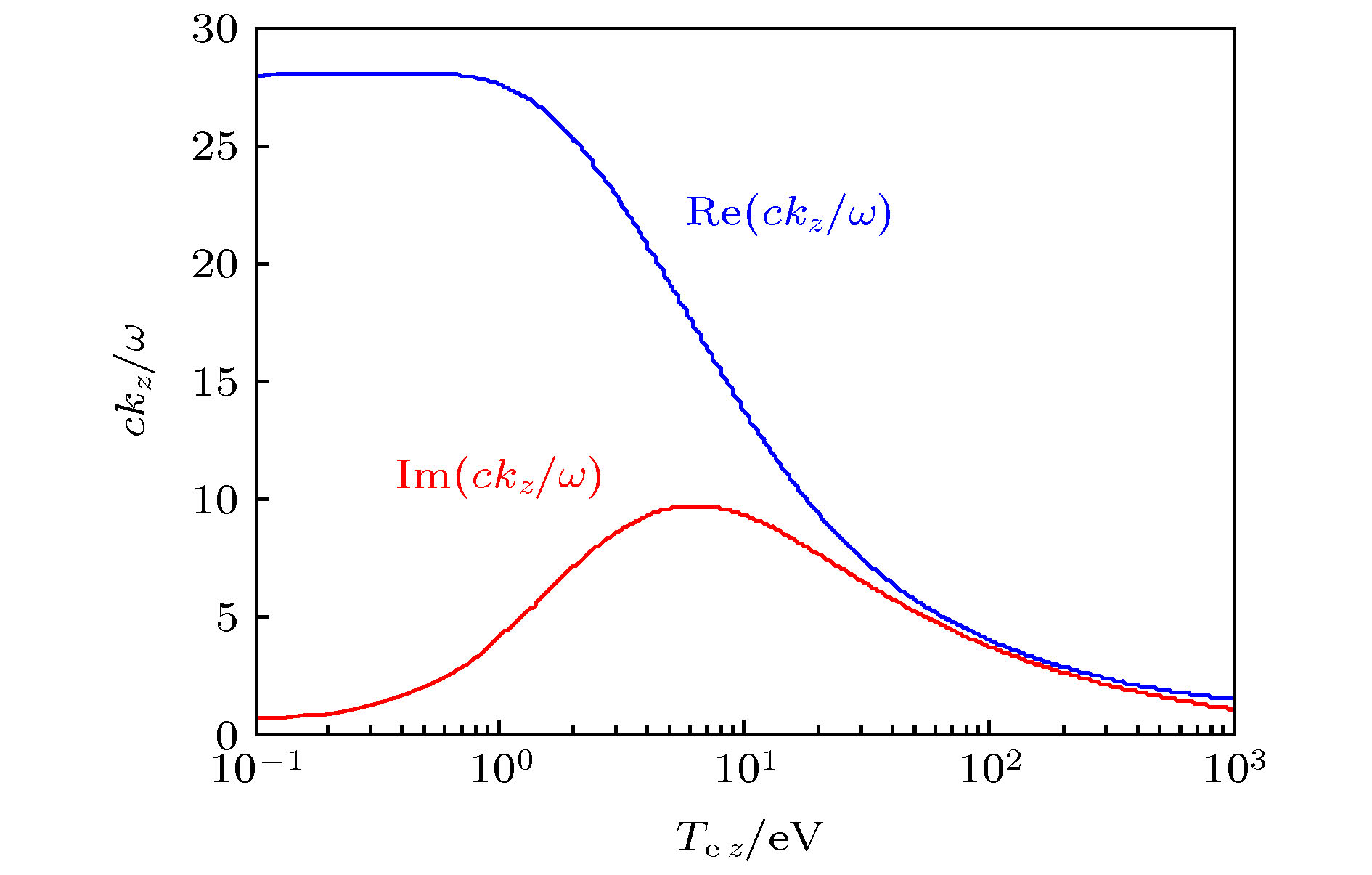
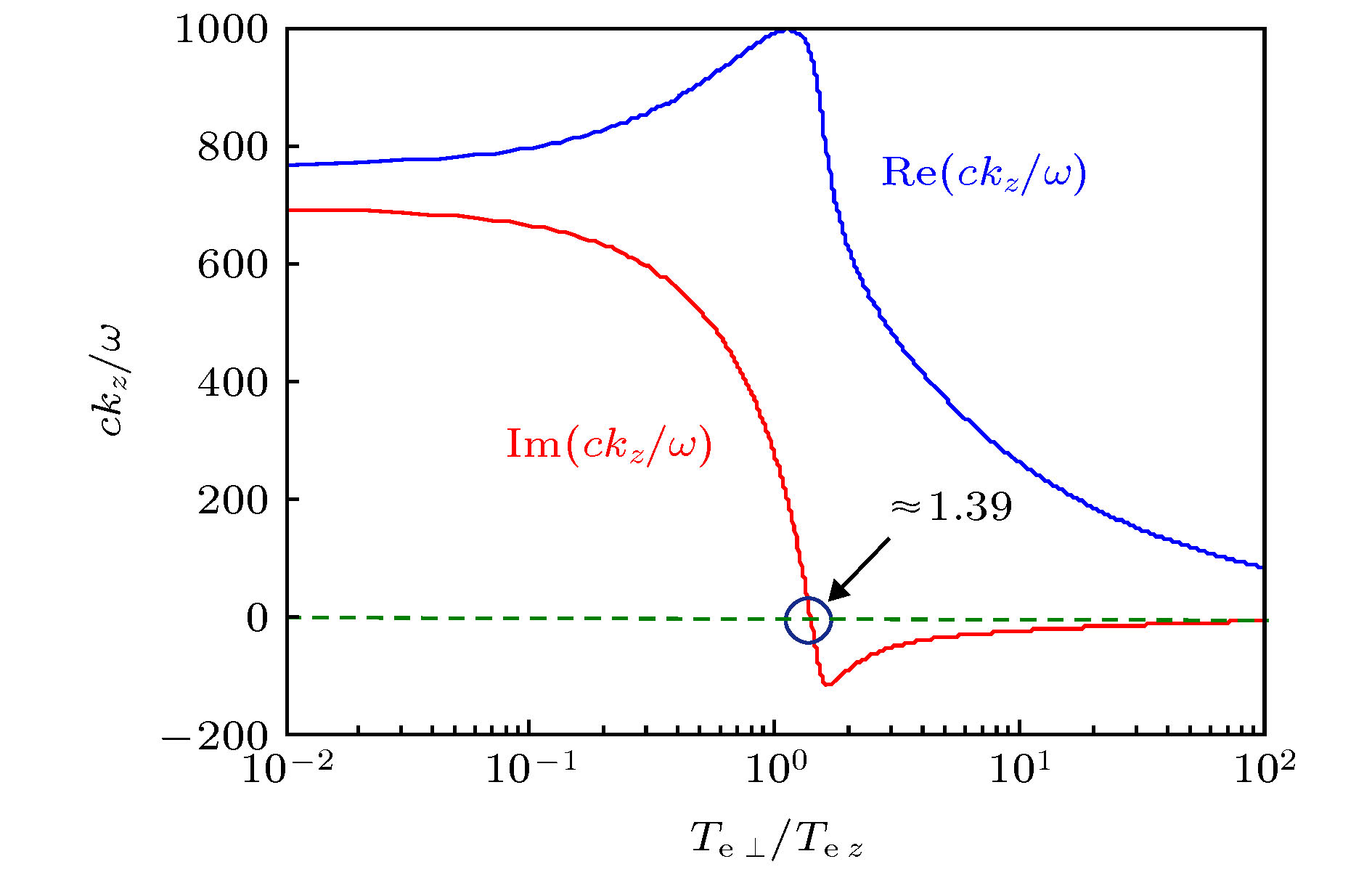
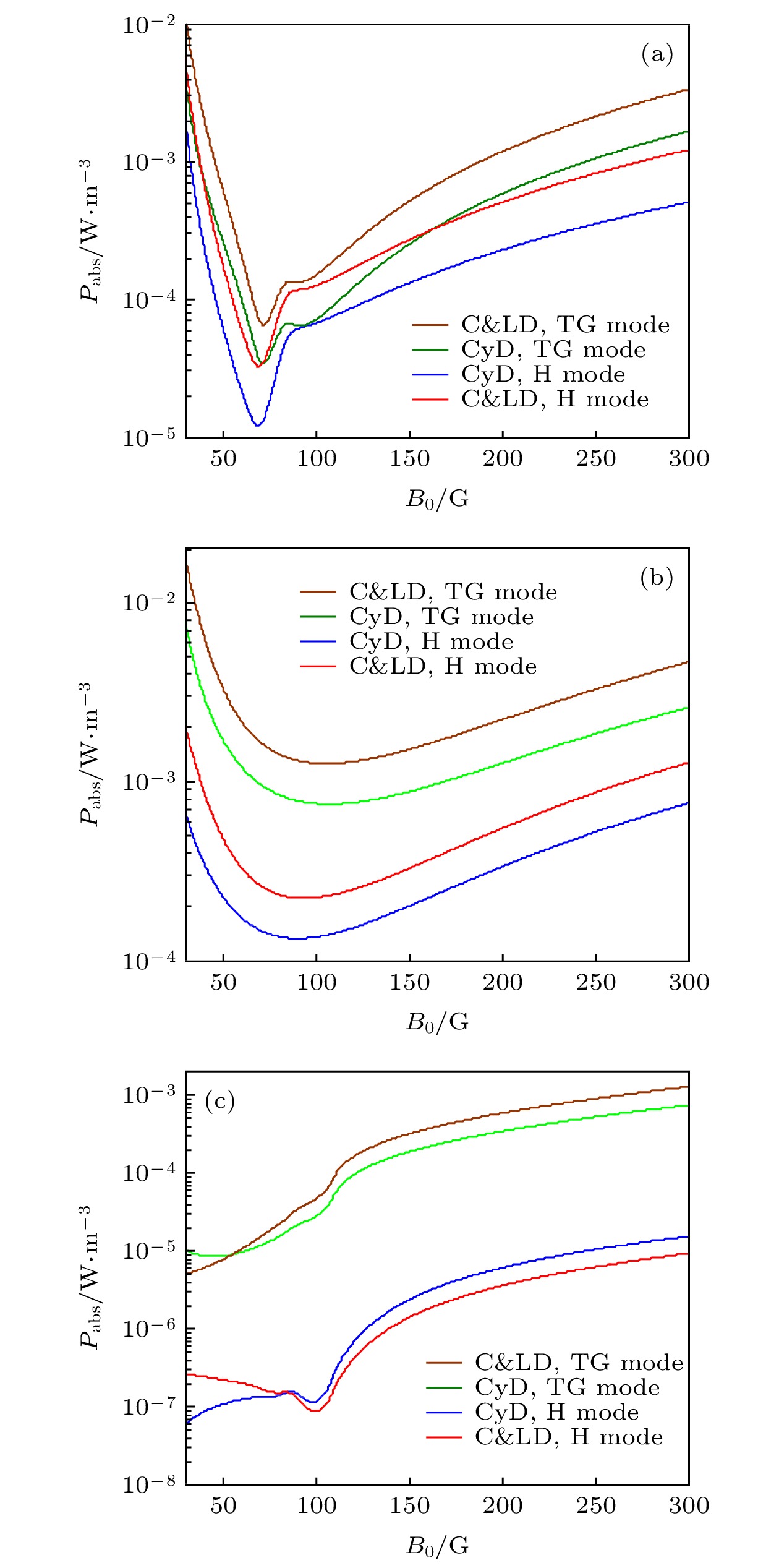
-
Understanding the power deposition characteristic of high density helicon wave plasma source is critical for further investigating into the discharge mechanism of helicon wave discharge. Based on the warm plasma dielectric tensor model which contains both the particle thermal effect and temperature anisotropy and using the insulting boundary condition, the eigenmode dispersion relation of helicon wave and Trivelpiece-Gould (TG) wave propagating in radially uniform plasma column are numerically obtained. Then based on the eigenmode dispersion relation and exact field distribution in the plasma column, the mode coupling properties between the helicon wave and TG wave, the parametric dependence of the cyclotron damping properties of the electron cyclotron wave (TG wave) and power deposition properties of the m = –1, 0, +1 modes under moderate plasma density and low magnetic fields conditions are theoretically investigated in typical helicon plasma parameter range. The detailed investigations are shown below. Under typical helicon plasma parameter conditions, i.e. wave frequency ω/2π = 13.56 MHz and the ion temperature is one-tenth of the electron temperature, there exist a critical magnetic field value B0,c and a critical electron temperature value Te,c for which under the conditions of B0 < B0,c the helicon wave becomes an evanescent wave and the TG wave becomes an evanescent wave when Te < Te,c. The cyclotron damping of the TG wave dramatically increases as the wave frequency approaches to the electron cyclotron frequency. The TG wave becomes a growth wave when the ratio of perpendicular electron temperature to parallel electron temperature is above a certain value. For the high magnetic field, i.e. ω/ωce = 0.1, most of the power deposition is deposited in the central core region, while for the low magnetic field, i.e. ω/ωce = 0.9, the power is deposited mainly in the outer region of plasma column. For typical helicon plasma electron temperature range, Te ∈ (3 eV, 5 eV), the energy depositions induced by the collisional damping and Landau damping of the TG wave are dominant for different electron temperature ranges, which implies that different damping mechanisms have different heating intensities for electrons. Under current parameter condition, compared with the m = +1 mode, the m = –1 and m = 0 mode of the TG wave play major role in the power deposition process, although the cyclotron damping of the TG wave dominates the power deposition in this typical electron temperature range. All these conclusions provide some useful clues for us to better understand the high ionization mechanism of helicon wave discharge.
-
Keywords:
- helicon plasma /
- mode coupling /
- power deposition /
- dispersion relation
[1] Diaz F R C 2000 Sci. Am. 283 90
[2] Boswell R W, Sutherland O, Charles C, et al. 2004 Phys. Plasmas 11 5125
Google Scholar
[3] Arefiev A V, Breizman B N 2004 Phys. Plasmas 11 2942
Google Scholar
[4] Donnelly V M, Kornblit A 2013 J. Vac. Sci. Technol., A 31 050825
Google Scholar
[5] Ho T M, Baturkin V, Grimm C, et al. 2017 Space Sci. Rev. 208 339
Google Scholar
[6] Mikouchi T, Komatsu M, Hagiya K, et al. 2014 Earth, Planets Space 66 1
Google Scholar
[7] Fiore G, Fedele R, de Angelis U 2014 Phys. Plasmas 21 113105
Google Scholar
[8] Reuter D C, Simon A A, Hair J, et al. 2018 Space Sci. Rev. 214 54
Google Scholar
[9] McMahon J W, Scheeres D J, Hesar S G, et al. 2018 Space Sci. Rev. 214 43
Google Scholar
[10] Bos B J, Ravine M A, Caplinger M, et al. 2018 Space Sci. Rev. 214 37
Google Scholar
[11] Shamrai K P, Taranov V B 1996 Plasma Sources Sci. Technol. 5 474
Google Scholar
[12] Shamrai K P 1998 Plasma Sources Sci. Technol. 7 499
Google Scholar
[13] Chen F F, Arnush D 1997 Phys. Plasmas 4 3411
Google Scholar
[14] Arnush D 2000 Phys. Plasmas 7 3042
Google Scholar
[15] Mouzouris Y, Scharer J E 1998 Phys. Plasmas 5 4253
Google Scholar
[16] Blackwell D D, Madziwa T G, Arnush D, et al. 2002 Phys. Rev. Lett. 88 145002
Google Scholar
[17] Kim S H, Hwang Y S 2008 Plasma Phys. Controlled Fusion 50 035007
Google Scholar
[18] Isayama S, Hada T, Shinohara S, et al. 2016 Phys. Plasmas 23 063513
Google Scholar
[19] 成玉国, 程谋森, 王墨戈, 等 2014 63 035203
Google Scholar
Cheng Y G, Cheng M S, Wang M G, et al. 2014 Acta Phys.Sin. 63 035203
Google Scholar
[20] 平兰兰, 张新军, 杨桦, 等 2019 68 205201
Google Scholar
Ping L L, Zhang X J, Yang H, et al. 2019 Acta Phys.Sin. 68 205201
Google Scholar
[21] Arnush D, Chen F F 1998 Phys. Plasmas 5 1239
Google Scholar
[22] Sakawa Y, Kunimatsu H, Kikuchi H, Fukui Y, Shoji T 2003 Phys. Rev. Lett. 90 105001
Google Scholar
[23] Huba J D 2016 NRL Plasma Formulary (Washington: Naval Research Laboratory) p34
[24] Fuchs V, Ram A K, Schultz S D, Bers A 1995 Phys. Plasmas 2 1637
Google Scholar
[25] Fried B D, Conte S D 2015 The Plasma Dispersion Function: the Hilbert Transform of the Gaussian (New York: Academic Press) pp1–3
[26] Gasimov G R, Abusutash Z A 2015 Int. J. Differ. Equ. Appl. 14 252
-
图 1 被绝缘边界包裹的等离子体柱横向截面示意图
Figure 1. Cross section of plasma column surround by insulating boundary.
图 2 (a) 静磁场与 (b) 电子温度对whistler waves的ES与EM分支耦合关系的影响
Figure 2. Influences of (a) magnetic field and (b) electron temperature on the mode coupling properties of ES and EM branches for whistler waves.
图 3 Whistler waves的色散关系
Figure 3. Dispersion relation of the whistler waves.
图 4 Whistler waves纵向波数的实部与虚部随纵向电子温度的变化关系
Figure 4. Corresponding relation of real and imaginary parts of the axial wave number of the whistler waves with the axial electron temperature.
图 5 Whistler waves纵向波数的实部与虚部随电子温度各向异性因子的变化关系
Figure 5. Corresponding relation of real and imaginary parts of the axial wave number of the whistler waves with the electron temperature anisotropy factor
图 6 总电场径向分布 (a), (b), (c) ω/ωce = 0.1; (d), (e), (f) ω/ωce = 0.9
Figure 6. Total electric field radial profiles for (a), (b), (c) ω/ωce = 0.1 and (d), (e), (f) ω/ωce = 0.9.
图 7 总功率沉积径向分布 (a), (b), (c) ω/ωce = 0.1; (d), (e), (f) ω/ωce = 0.9
Figure 7. Radial distributions of the total power deposition for: (a), (b), (c) ω/ωce = 0.1 and (d), (e), (f) ω/ωce = 0.9.
图 8 螺旋波与TG波的功率沉积随轴向静磁场的变化 (a) m = –1 模; (b) m = 0 模; (c) m = +1 模
Figure 8. Power deposition profiles of the helicon and TG waves are given as functions of axial static magnetic fields for (a) m = –1 mode; (b) m = 0 mode; (c) m = +1 mode.
图 9 螺旋波与TG波功率沉积随电子温度的变化 (a) m = –1 模; (b) m = 0 模; (c) m = +1 模
Figure 9. Power deposition profiles of helicon and TG waves are given as functions of electron temperature for (a) m = –1 mode; (b) m = 0 mode; (c) m = +1 mode.
图 10 螺旋波与TG波的碰撞阻尼和朗道阻尼致使的功率沉积随电子温度的变化 (a) m = –1 模; (b) m = 0 模
Figure 10. Power deposition profiles induced by the collisional damping and Landau damping of helicon and TG waves are given as functions of electron temperature for (a) m = –1 mode; (b) m = 0 mode.
表 1 本征模色散关系元素
Table 1. Elements of eigenmode dispersion relation.
${Q_{s\ell }}$ $\ell = 1$ $\ell = {\rm{2}}$ $\ell = {\rm{3}}$ $s = 1$ ${{\rm{J}}_m}({k_{ \bot , {\rm{H}}}}a)$ ${{\rm{J}}_m}({k_{ \bot , TG}}a)$ $- {\rm{j} }{k_{ \bot , v} }{\rm{H} }_m^{(1)}({k_{ \bot , v} }a)$ $s = {\rm{2}}$ $k_{ \bot , {\rm{TG} } }^2[ m{k_z}{ {\rm{J} }_m}({k_{ \bot , {\rm{H} } } }a) \\ +{\beta _1}{k_{ \bot , {\rm{H} } } }a {\rm{J} }_m^\prime ({k_{ \bot , {\rm{H} } } }a) ]$ $k_{ \bot , {\rm{H} } }^2[ m{k_z}{ {\rm{J} }_m}({k_{ \bot , {\rm{TG} } } }a) \\ +{\beta _2}{k_{ \bot , {\rm{TG} } } }a {\rm{J} }_m^\prime ({k_{ \bot , {\rm{TG} } } }a) ]$ ${\rm{j} }k_{ \bot , {\rm{H} } }^2 k_{ \bot , {\rm{TG} } }^2 m{\rm{H} }_m^{(1)}({k_{ \bot , v} }a)$ $s = {\rm{3}}$ $k_{ \bot , {\rm{TG} } }^2[ m{\beta _1}{ {\rm{J} }_m}({k_{ \bot , {\rm{H} } } }a) \\ +{k_z}{k_{ \bot , {\rm{H} } } }a {\rm{J} }_m^\prime ({k_{ \bot , {\rm{H} } } }a) ]$ $k_{ \bot , {\rm{H} } }^2[ m{\beta _2}{ {\rm{J} }_m}({k_{ \bot , {\rm{TG} } } }a) \\ +{k_z}{k_{ \bot , {\rm{TG} } } }a {\rm{J} }_m^\prime ({k_{ \bot , {\rm{TG} } } }a) ]$ ${\rm{j} }k_{ \bot , {\rm{H} } }^2 k_{ \bot , {\rm{TG} } }^2{k_{ \bot , v} }a{\rm{H} }_m^{(1)\prime }({k_{ \bot , v} }a)$ 
DownLoad: CSV
-
[1] Diaz F R C 2000 Sci. Am. 283 90
[2] Boswell R W, Sutherland O, Charles C, et al. 2004 Phys. Plasmas 11 5125
Google Scholar
[3] Arefiev A V, Breizman B N 2004 Phys. Plasmas 11 2942
Google Scholar
[4] Donnelly V M, Kornblit A 2013 J. Vac. Sci. Technol., A 31 050825
Google Scholar
[5] Ho T M, Baturkin V, Grimm C, et al. 2017 Space Sci. Rev. 208 339
Google Scholar
[6] Mikouchi T, Komatsu M, Hagiya K, et al. 2014 Earth, Planets Space 66 1
Google Scholar
[7] Fiore G, Fedele R, de Angelis U 2014 Phys. Plasmas 21 113105
Google Scholar
[8] Reuter D C, Simon A A, Hair J, et al. 2018 Space Sci. Rev. 214 54
Google Scholar
[9] McMahon J W, Scheeres D J, Hesar S G, et al. 2018 Space Sci. Rev. 214 43
Google Scholar
[10] Bos B J, Ravine M A, Caplinger M, et al. 2018 Space Sci. Rev. 214 37
Google Scholar
[11] Shamrai K P, Taranov V B 1996 Plasma Sources Sci. Technol. 5 474
Google Scholar
[12] Shamrai K P 1998 Plasma Sources Sci. Technol. 7 499
Google Scholar
[13] Chen F F, Arnush D 1997 Phys. Plasmas 4 3411
Google Scholar
[14] Arnush D 2000 Phys. Plasmas 7 3042
Google Scholar
[15] Mouzouris Y, Scharer J E 1998 Phys. Plasmas 5 4253
Google Scholar
[16] Blackwell D D, Madziwa T G, Arnush D, et al. 2002 Phys. Rev. Lett. 88 145002
Google Scholar
[17] Kim S H, Hwang Y S 2008 Plasma Phys. Controlled Fusion 50 035007
Google Scholar
[18] Isayama S, Hada T, Shinohara S, et al. 2016 Phys. Plasmas 23 063513
Google Scholar
[19] 成玉国, 程谋森, 王墨戈, 等 2014 63 035203
Google Scholar
Cheng Y G, Cheng M S, Wang M G, et al. 2014 Acta Phys.Sin. 63 035203
Google Scholar
[20] 平兰兰, 张新军, 杨桦, 等 2019 68 205201
Google Scholar
Ping L L, Zhang X J, Yang H, et al. 2019 Acta Phys.Sin. 68 205201
Google Scholar
[21] Arnush D, Chen F F 1998 Phys. Plasmas 5 1239
Google Scholar
[22] Sakawa Y, Kunimatsu H, Kikuchi H, Fukui Y, Shoji T 2003 Phys. Rev. Lett. 90 105001
Google Scholar
[23] Huba J D 2016 NRL Plasma Formulary (Washington: Naval Research Laboratory) p34
[24] Fuchs V, Ram A K, Schultz S D, Bers A 1995 Phys. Plasmas 2 1637
Google Scholar
[25] Fried B D, Conte S D 2015 The Plasma Dispersion Function: the Hilbert Transform of the Gaussian (New York: Academic Press) pp1–3
[26] Gasimov G R, Abusutash Z A 2015 Int. J. Differ. Equ. Appl. 14 252
DownLoad:
Catalog
Metrics
- Abstract views: 4879
- PDF Downloads: 71
- Cited By: 0
