-
In recent years, it has been a hot research topic to study the interaction between atomic ensemble and cavities, and many researches have been done in this regard. In such a system, some atoms are trapped in the cavity, which can be used to study their dynamic characteristics, e.g., the evolution of photon numbers and photon transition. The Jaynes-Cummings model is an important model for studying the dynamic characteristics of the cavity-atom system, which is based on the interaction between a single two-level atom and the cavity field. Recently, coherent photon control in cavity under specific conditions has become an important part of quantum computing and communication. It is worth noting that the tunable photon transmission and all-optical switches based on the cavity have already aroused much interest and have been used in many areas. The quantum information and networks are mostly rooted in complex optical devices, which may show nonreciprocal or asymmetric photon transport. In this paper, we demonstrate that by using an optical closed-loop system the unconventional photon transport can be realized with two mutually perpendicular cavities coupled through external fiber and a two-level atom placed on the intersection. This three-mode system supports two orthogonal propagation directions, that is to say, and the interactions among probe fields are mutually perpendicular. Without ignoring the spontaneous decay of the natural atom, the complex and controllable quantum interference induced by the efficient hybrid interaction of the light, cavity modes, and the atom in such a closed-loop structure can result in a few interesting symmetric and asymmetric photon transport behaviors, i.e. coherent perfect synthesis and coherent perfect reflection. Aside from these compelling properties, the group velocity can also be modulated, i.e., fast and slow light effect. All of these processes can be dynamically controlled by using the probe field phase difference, the tunneling coupling between two cavities and the coupling between the cavity and the atom. Importantly, due to so many advantages, such a tunable scheme can be readily extended to some optical devices, e.g., the switch and the router that is challenging to conventional optical devices.
[1] Mabuchi H, Doherty A C 2002 Science 298 1372
Google Scholar
[2] Vahala K J 2003 Nature (London) 424 839
Google Scholar
[3] Aoki T, Parkins A S, Alton D J, Regal C A, Dayan B, Ostby E, Vahala K J, Kimble H J 2009 Phys. Rev. Lett. 102 083601
Google Scholar
[4] Zhou L, Yang L P, Li Y, Sun C P 2013 Phys. Rev. Lett. 111 103604
Google Scholar
[5] Lu J, Zhou L, Kuang L M, Nori F 2014 Phys. Rev. A 89 013805
Google Scholar
[6] Hong F Y, Xiong S J 2008 Phys. Rev. A 78 013812
Google Scholar
[7] Li J, Zhang S, Yu R, Zhang D, Wu Y 2014 Phys. Rev. A 90 053832
Google Scholar
[8] Li J, Yu R, Ma J, Wu Y 2015 Phys. Rev. A 91 063834
Google Scholar
[9] Li J, Li J, Xiao Q, Wu Y 2016 Phys. Rev. A 93 063814
Google Scholar
[10] Agarwal G S, Zhu Y 2015 Phys. Rev. A 92 023824
Google Scholar
[11] Agarwal G S, Di K, Wang L, Zhu Y 2016 Phys. Rev. A 93 063805
Google Scholar
[12] Wang L, Di K, Zhu Y, Agarwal G S 2017 Phys. Rev. A 95 013841
Google Scholar
[13] Lu J, Wang Z H, Zhou L 2015 Opt.Express 23 022955
Google Scholar
[14] Yan W B, Huang J F, Fan H 2015 Sci.Rep. 3 3555
[15] Kimble H J 2008 Nature (London) 453 1023
Google Scholar
[16] Stannigel K, Komar P, Habraken S J M, Bennett S D, Lukin M D, Zoller P, Rabl P 2012 Phys .Rev. Lett. 109 013603
Google Scholar
[17] Giunter G, Anappara A A, Hees J, Sell A, Biasiol G, Sorba L, De Liberato S, Ciuti C, Tredicucci A, Leitenstorfer A, Huber R 2009 Nature (London) 458 178
Google Scholar
[18] Nozaki K, Tanabe T, Shinya A, Matsuo S, Sato T, Taniyama H, Notomi M 2010 Nat. Photonics 4 477
Google Scholar
[19] Yan X B, Cui C L, Gu K H, Tian X D, Fu C B, Wu J H 2014 Opt. Express 22 004886
Google Scholar
[20] Liu Y L, Wu R, Zhang J, Ozdemir S K, Yang L, Nori F, Liu Y X 2017 Phys. Rev. A 95 013843
Google Scholar
[21] Zhang X Y, Guo Y Q, Pei P, Yi X X 2017 Phys. Rev. A 95 063825
Google Scholar
[22] Bajcsy M, Hofferberth S, Balic V, Peyronel T, Hafezi M, Zibrov A S, Vuletic V, Lukin M D 2009 Phys. Rev. Lett. 102 203902
Google Scholar
[23] Tanabe T, Notomi M, Mitsugi S, Shinya A, Kuramochi E 2005 Opt. Lett. 30 002575
Google Scholar
[24] Volz T, Reinhard A, Winger M, Badolato A, Hennessy K J, Hu E L 2012 Nat. Photonics 6 605
Google Scholar
[25] Tiecke T G, Thompson J D, de Leon N P, Liu L R, Vuleti’c V, Lukin M D 2014 Nature (London) 508 241
Google Scholar
[26] Cirac J I, Zoller P, Kimble H J, Mabuchi H 1997 Phys. Rev. Lett. 78 3221
Google Scholar
[27] Dawes A M C, Illing L, Clark S M, Gauthier D J 2005 Science 308 5722
[28] Duan L M, Monroe C 2010 Rev. Mod. Phys. 82 1209
Google Scholar
[29] Bouwmeester D, Ekert A K, Zeilinger A 2000 The Physics of Quantum Information (New York: Springer) pp133−135
[30] Weis S, Riviere R, Deleglise S, Gavartin E, Arcizet O, Schliesser A, Kippenberg T J 2010 Science 330 1520
Google Scholar
[31] Chan J, Alegre T P M, Safavi-Naeini A H, Hill J T, Krause A, Groblacher S, Aspelmeyer M, Painter O 2011 Nature (London) 478 89
Google Scholar
[32] Verhagen E, Deleglise S, Weis S A, Kippenberg T J 2012 Nature (London) 482 63
Google Scholar
[33] Liu X Y, Jing H, Ma J Y, Wu Y 2015 Phys. Rev. Lett. 114 253601
Google Scholar
[34] Du L, Fan C H, Zhang H X, Wu J H 2017 Sci. Rep. 7 15834
Google Scholar
[35] Manipatruni S, Robinson J T, Lipson M 2009 Phys. Rev. Lett. 102 213903
Google Scholar
[36] Agarwal G S, Huang S 2010 Phys. Rev. A 81 041803
Google Scholar
[37] Xu X W, Li Y, Chen A X, Liu Y X 2016 Phys. Rev. A 93 023827
Google Scholar
[38] Du L, Liu Y M, Jiang B, Zhang Y 2018 EPL 122 24001
Google Scholar
[39] Jiang C, Song L N, Li Y 2019 Phys. Rev. A 99 023823
Google Scholar
[40] Malz D, Toth L D, Bernier N R, Feofanov A K, Kippenberg T J, Nunnenkamp A 2018 Phys.Rev.Lett. 120 023601
Google Scholar
[41] Safavi-Naeini A H, Mayer A T P, Chan J, Eichenfield M, Winger M, Lin Q, Hill J T, Chang D E, Painter O 2011 Nature (London) 472 69
Google Scholar
[42] Asano M, Ozdemir S K, Chen W, Ikuta R, Yang L, Imoto N, Yamamoto T 2016 Phys. Rev. Lett. 108 181105
[43] Li J H, Zhan X G, Ding C L, Zhang D, Wu Y 2015 Phys. Rev. A 92 043830
Google Scholar
[44] Du L, Zhang Y, Fan C H, Liu Y M, Gao F, Wu J H 2018 Sci. Rep. 8 2933
Google Scholar
[45] Colombe1 Y, Steinmetzl T, Dubois1 G, Linke1 F, Hunger D, Reichel1 J 2007 Nature (London) 450 272
Google Scholar
[46] Hattermann1 H, Bothner1 D, Ley1 L Y, Ferdinand1 B, Wiedmaier1 D, Sarkany1 L, Kleiner1 R, Koelle1 D, Fortagh1 J 2017 Nat. Commun. 8 2254
Google Scholar
[47] Farace A, Giovannetti V 2012 Phys. Rev. A 86 013820
Google Scholar
[48] Walls D F, Milburn G J 1994 Quantum Optics (Berlin: Springer Verlag) pp127−141
[49] Gardiner C W, Zoller P 2004 Quantum Noise (Berlin: Springer) pp158−170
[50] Cao C, Chen X, Duan Y W 2018 Optik 161 293
Google Scholar
-
图 1 (a)由两个光学腔模和原子组成的闭环三模系统图; (b)正交腔结构的装置图
Figure 1. (a) Schematic diagram of an optical system composed of two optical cavities and the atomic ensemble; (b) realistic setup of that optical system with the double-cavity orthogonal structure.
图 2 当隧穿强度
$J = 0, 3\kappa, 6\kappa $ , 归一化输出场强度${I_{\rm a}}$ (${I_{\rm b}}$ )随输入场失谐$\varDelta /\kappa$ 的变化情况 (a)$\theta = 0$ ; (b)$\theta = \dfrac{{\text{π}}}{2}$ (a腔),$\theta = \dfrac{{3{\text{π}}}}{2}$ (b腔); (c)$\theta = {\text{π}}$ ; (d)$\theta = \dfrac{{\text{π}}}{2}$ (b腔),$\theta = \dfrac{{3{\text{π}}}}{2}$ (a腔). 其他参数分别为${g_0} = 2\kappa $ ,$\gamma = 2\kappa $ ,$\kappa = 1$ Figure 2. Normalized output field intensities
${I_{\rm a}}$ vs. normalized input field detuning$\varDelta /\kappa$ with tunneling strength$J = 0, 3\kappa, 6\kappa $ : (a)$\theta = 0$ ; (b)$\theta = \dfrac{{\text{π}}}{2}$ (cavity-a),$\theta = \dfrac{{3{\text{π}}}}{2}$ (cavity-b); (c)$\theta = {\text{π}}$ ; (d)$\theta = \dfrac{{\text{π}}}{2}$ (cavity-b),$\theta = \dfrac{{3{\text{π}}}}{2}$ (cavity-a). Other parameters are${g_0} = 2\kappa $ ,$\gamma = 2\kappa $ ,$\kappa = 1$ .
图 3 归一化输出场强度
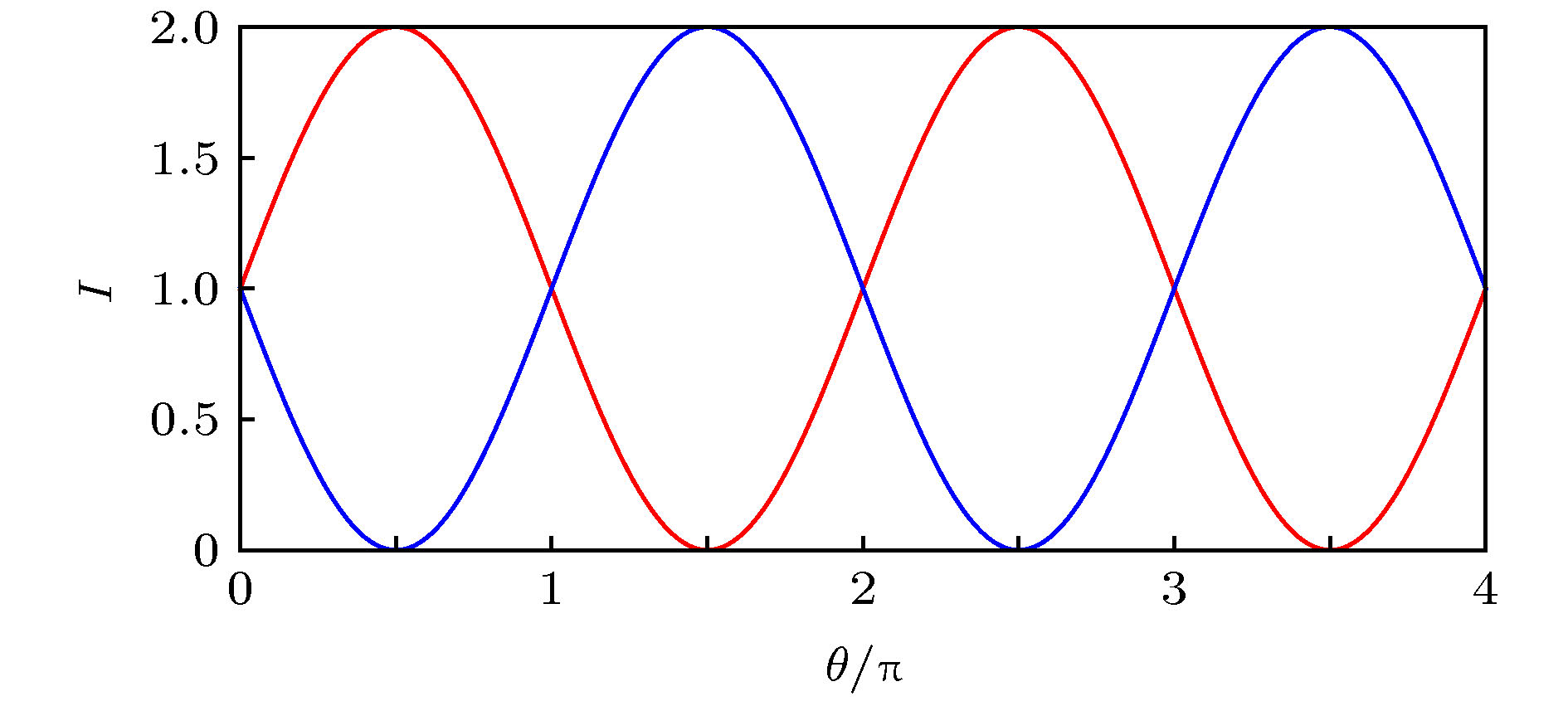
${I_{\rm a}}$ (红色线)和${I_{\rm b}}$ (蓝色线)随相对相位$\theta $ 变化情况. 其他参数为$\varDelta = 4.88\kappa$ ,$J = 6\kappa $ ,${g_0} = \kappa $ ,$\gamma = 2\kappa $ ,$\kappa = 1$ Figure 3. Normalized output field intensities
${I_{\rm a}}$ (red-line) and${I_{\rm b}}$ (blue-line) vs. the relative phase$\theta $ with$\varDelta = 4.88\kappa$ . Other parameters are$J = 6\kappa $ ,${g_0} = \kappa $ ,$\gamma = 2\kappa $ ,$\kappa = 1$ .
图 4 输出群延迟
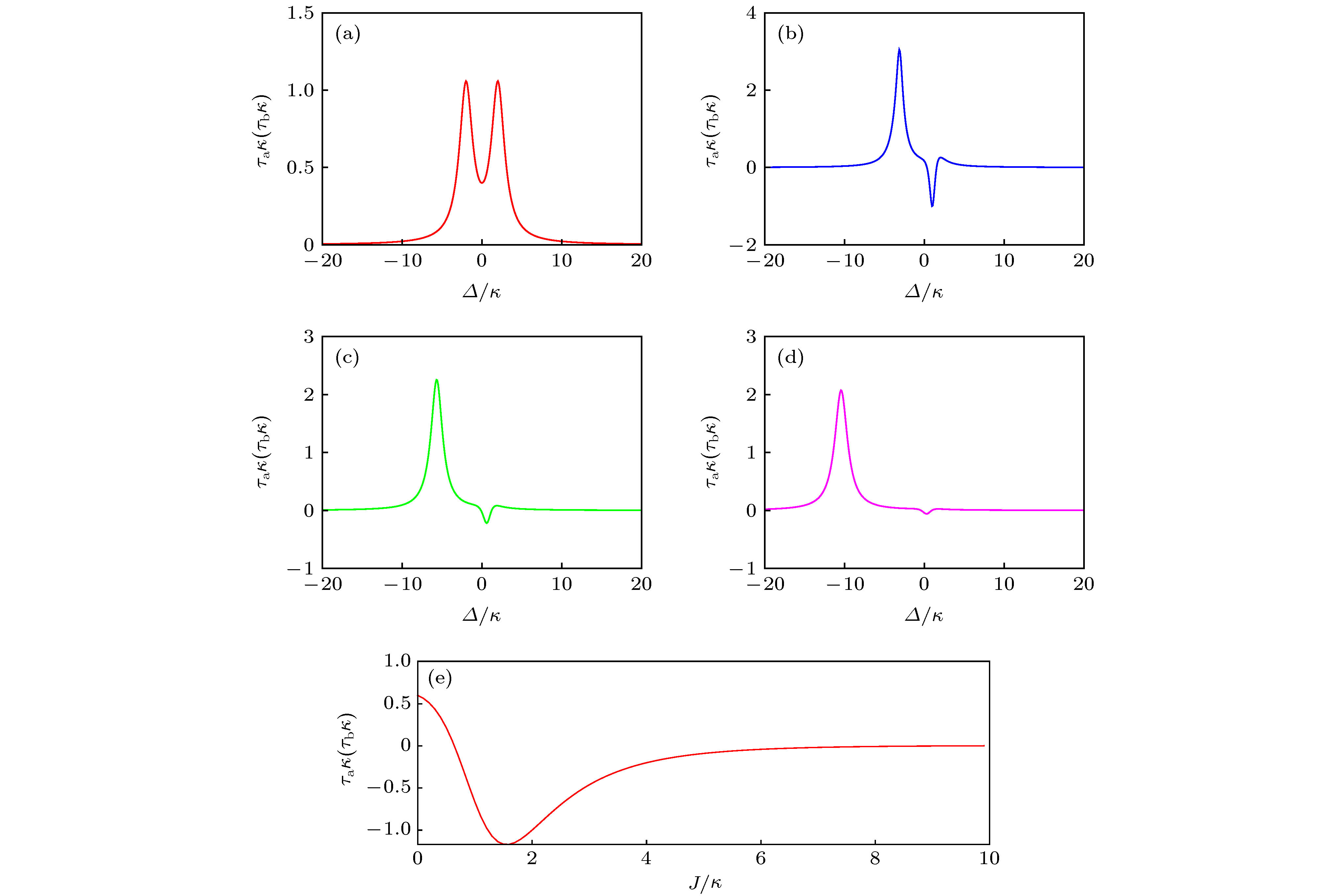
${\tau _{\rm a}}\kappa$ (${\tau _{\rm b}}\kappa$ )随输入场失谐$\varDelta /\kappa$ 变化情况, 其中隧穿强度为 (a)$J = 0$ , (b)$J = \kappa $ , (c)$J = 2\kappa $ , (d)$J = 3\kappa $ ; (e)输出群延迟${\tau _a}\kappa $ (${\tau _b}\kappa $ )与隧穿强度$J/\kappa $ 在$\varDelta /\kappa = 1$ 时的关系图. 其他参数为${g_0} = 2\kappa $ ,$\gamma = 2\kappa $ ,$\kappa = 1$ Figure 4. Normalized output group delay
${\tau _{\rm a}}\kappa$ (${\tau _{\rm b}}\kappa$ ) vs. normalized input field detuning$\varDelta /\kappa$ with tunneling strength of (a)$J = 0$ ,(b)$J = \kappa $ , (c)$J = 2\kappa $ , (d)$J = 3\kappa $ ; (e) output group delay${\tau _{\rm a}}\kappa$ (${\tau _{\rm b}}\kappa$ ) vs. normalized tunneling strength$J/\kappa $ for$\varDelta /\kappa = 1$ . Other parameters are${g_0} = 2\kappa $ ,$\gamma = 2\kappa $ ,$\kappa = 1$ . -
[1] Mabuchi H, Doherty A C 2002 Science 298 1372
Google Scholar
[2] Vahala K J 2003 Nature (London) 424 839
Google Scholar
[3] Aoki T, Parkins A S, Alton D J, Regal C A, Dayan B, Ostby E, Vahala K J, Kimble H J 2009 Phys. Rev. Lett. 102 083601
Google Scholar
[4] Zhou L, Yang L P, Li Y, Sun C P 2013 Phys. Rev. Lett. 111 103604
Google Scholar
[5] Lu J, Zhou L, Kuang L M, Nori F 2014 Phys. Rev. A 89 013805
Google Scholar
[6] Hong F Y, Xiong S J 2008 Phys. Rev. A 78 013812
Google Scholar
[7] Li J, Zhang S, Yu R, Zhang D, Wu Y 2014 Phys. Rev. A 90 053832
Google Scholar
[8] Li J, Yu R, Ma J, Wu Y 2015 Phys. Rev. A 91 063834
Google Scholar
[9] Li J, Li J, Xiao Q, Wu Y 2016 Phys. Rev. A 93 063814
Google Scholar
[10] Agarwal G S, Zhu Y 2015 Phys. Rev. A 92 023824
Google Scholar
[11] Agarwal G S, Di K, Wang L, Zhu Y 2016 Phys. Rev. A 93 063805
Google Scholar
[12] Wang L, Di K, Zhu Y, Agarwal G S 2017 Phys. Rev. A 95 013841
Google Scholar
[13] Lu J, Wang Z H, Zhou L 2015 Opt.Express 23 022955
Google Scholar
[14] Yan W B, Huang J F, Fan H 2015 Sci.Rep. 3 3555
[15] Kimble H J 2008 Nature (London) 453 1023
Google Scholar
[16] Stannigel K, Komar P, Habraken S J M, Bennett S D, Lukin M D, Zoller P, Rabl P 2012 Phys .Rev. Lett. 109 013603
Google Scholar
[17] Giunter G, Anappara A A, Hees J, Sell A, Biasiol G, Sorba L, De Liberato S, Ciuti C, Tredicucci A, Leitenstorfer A, Huber R 2009 Nature (London) 458 178
Google Scholar
[18] Nozaki K, Tanabe T, Shinya A, Matsuo S, Sato T, Taniyama H, Notomi M 2010 Nat. Photonics 4 477
Google Scholar
[19] Yan X B, Cui C L, Gu K H, Tian X D, Fu C B, Wu J H 2014 Opt. Express 22 004886
Google Scholar
[20] Liu Y L, Wu R, Zhang J, Ozdemir S K, Yang L, Nori F, Liu Y X 2017 Phys. Rev. A 95 013843
Google Scholar
[21] Zhang X Y, Guo Y Q, Pei P, Yi X X 2017 Phys. Rev. A 95 063825
Google Scholar
[22] Bajcsy M, Hofferberth S, Balic V, Peyronel T, Hafezi M, Zibrov A S, Vuletic V, Lukin M D 2009 Phys. Rev. Lett. 102 203902
Google Scholar
[23] Tanabe T, Notomi M, Mitsugi S, Shinya A, Kuramochi E 2005 Opt. Lett. 30 002575
Google Scholar
[24] Volz T, Reinhard A, Winger M, Badolato A, Hennessy K J, Hu E L 2012 Nat. Photonics 6 605
Google Scholar
[25] Tiecke T G, Thompson J D, de Leon N P, Liu L R, Vuleti’c V, Lukin M D 2014 Nature (London) 508 241
Google Scholar
[26] Cirac J I, Zoller P, Kimble H J, Mabuchi H 1997 Phys. Rev. Lett. 78 3221
Google Scholar
[27] Dawes A M C, Illing L, Clark S M, Gauthier D J 2005 Science 308 5722
[28] Duan L M, Monroe C 2010 Rev. Mod. Phys. 82 1209
Google Scholar
[29] Bouwmeester D, Ekert A K, Zeilinger A 2000 The Physics of Quantum Information (New York: Springer) pp133−135
[30] Weis S, Riviere R, Deleglise S, Gavartin E, Arcizet O, Schliesser A, Kippenberg T J 2010 Science 330 1520
Google Scholar
[31] Chan J, Alegre T P M, Safavi-Naeini A H, Hill J T, Krause A, Groblacher S, Aspelmeyer M, Painter O 2011 Nature (London) 478 89
Google Scholar
[32] Verhagen E, Deleglise S, Weis S A, Kippenberg T J 2012 Nature (London) 482 63
Google Scholar
[33] Liu X Y, Jing H, Ma J Y, Wu Y 2015 Phys. Rev. Lett. 114 253601
Google Scholar
[34] Du L, Fan C H, Zhang H X, Wu J H 2017 Sci. Rep. 7 15834
Google Scholar
[35] Manipatruni S, Robinson J T, Lipson M 2009 Phys. Rev. Lett. 102 213903
Google Scholar
[36] Agarwal G S, Huang S 2010 Phys. Rev. A 81 041803
Google Scholar
[37] Xu X W, Li Y, Chen A X, Liu Y X 2016 Phys. Rev. A 93 023827
Google Scholar
[38] Du L, Liu Y M, Jiang B, Zhang Y 2018 EPL 122 24001
Google Scholar
[39] Jiang C, Song L N, Li Y 2019 Phys. Rev. A 99 023823
Google Scholar
[40] Malz D, Toth L D, Bernier N R, Feofanov A K, Kippenberg T J, Nunnenkamp A 2018 Phys.Rev.Lett. 120 023601
Google Scholar
[41] Safavi-Naeini A H, Mayer A T P, Chan J, Eichenfield M, Winger M, Lin Q, Hill J T, Chang D E, Painter O 2011 Nature (London) 472 69
Google Scholar
[42] Asano M, Ozdemir S K, Chen W, Ikuta R, Yang L, Imoto N, Yamamoto T 2016 Phys. Rev. Lett. 108 181105
[43] Li J H, Zhan X G, Ding C L, Zhang D, Wu Y 2015 Phys. Rev. A 92 043830
Google Scholar
[44] Du L, Zhang Y, Fan C H, Liu Y M, Gao F, Wu J H 2018 Sci. Rep. 8 2933
Google Scholar
[45] Colombe1 Y, Steinmetzl T, Dubois1 G, Linke1 F, Hunger D, Reichel1 J 2007 Nature (London) 450 272
Google Scholar
[46] Hattermann1 H, Bothner1 D, Ley1 L Y, Ferdinand1 B, Wiedmaier1 D, Sarkany1 L, Kleiner1 R, Koelle1 D, Fortagh1 J 2017 Nat. Commun. 8 2254
Google Scholar
[47] Farace A, Giovannetti V 2012 Phys. Rev. A 86 013820
Google Scholar
[48] Walls D F, Milburn G J 1994 Quantum Optics (Berlin: Springer Verlag) pp127−141
[49] Gardiner C W, Zoller P 2004 Quantum Noise (Berlin: Springer) pp158−170
[50] Cao C, Chen X, Duan Y W 2018 Optik 161 293
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6405
- PDF Downloads: 105
- Cited By: 0
