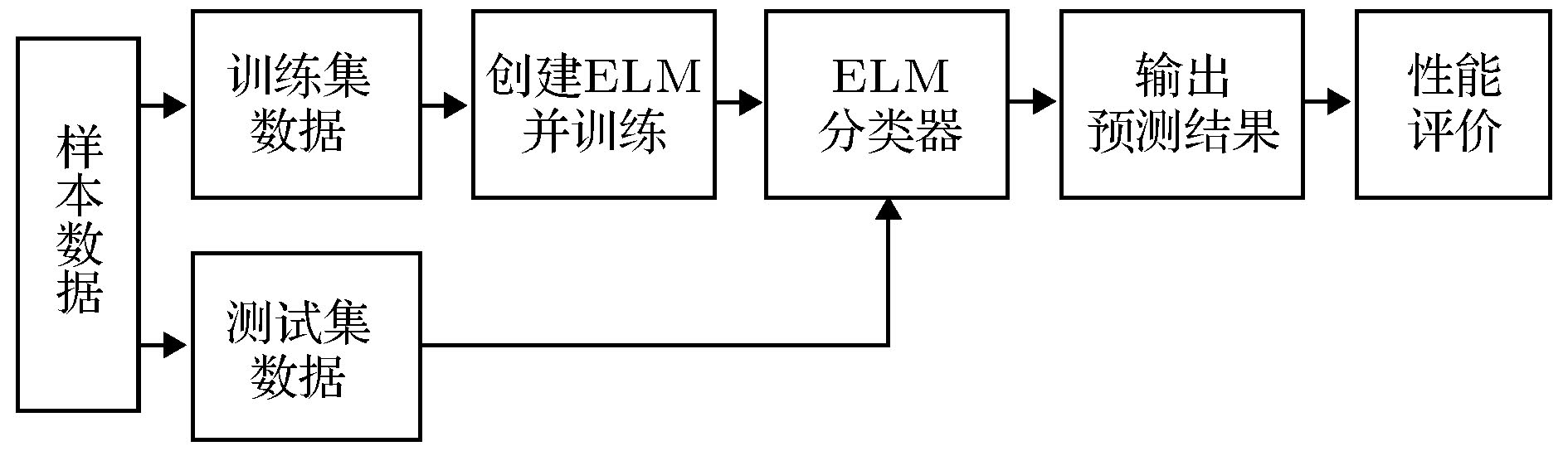
-
At present, resting state functional magnetic resonance imaging (rfMRI) has provided an efficient, rapid and advanced technology for brain function detection. Entropy can capture the dynamic characteristics of neural signals and might be used as a quantitative evaluation parameter. However, there are some problems remain solved yet, such as the entropy model computing with a fixed scale, and whether the entropy model could evaluate the cognitive performance.These problems will affect the accuracy of detection. Therefore, the multi-scale entropy model combined with a machine learning method is proposed here to investigate the relationship between complexity derived from BOLD signal and cognitive score of healthy elderly people, so as to some new imaging biomarkers could be illuminate by rfMRI. A total of 98 healthy old volunteers were selected and divided into two groups according to the pre-scan scores for the cognitive questions test (regarded as cognitive performance here): excellent group and poor group. Firstly, the multi-scale entropy model was constructed, the entropy of scanning data was calculated in two groups, and the parameters of the model were optimized by statistics and comparison with the help machine learning method. Secondly, the eigenvectors were constructed by the entropy values of the indicative brain areas with high statistical significance under the optimized parameters of multi-scale model. Finally, the sample data were divided into either training set or testing set, in which 78 people were randomly included in the training set and the rest of 20 people were included in the testing set. The two groups of data were classified and tested by the extreme learning machine. It was found that there was a significant difference between the frontal and temporal regions in the assessment of cognitive scores of the elderly by the multi-scale entropy model based on rfMRI, and the sorting rate for the cognitive scores could reach up to 80%. Conclusion: the optimized multi-scale entropy model can effectively distinguish the cognitive scores of healthy elderly people at the frontal lobe, temporal lobe and other marker brain regions. This study has highlighted the optimization advantage of the multi-scale entropy model with the help of machine learning, and might provide a new detection parameter and a potential method for rfMRI to replace the subjective and tedious traditional cognitive scale form tests.
-
Keywords:
- multi-scale entropy /
- resting-state fMRI /
- extreme learning machine /
- cognitive score
[1] Costa M, Goldberger A, Peng C K 2002 Phys. Rev. Lett. 89 068102
Google Scholar
[2] Rosso O A, Martin M T, PlastinoA 2002 Phys. A 313 587
Google Scholar
[3] 姚文坡, 刘铁兵, 戴加飞, 王俊 2014 63 078704
Yao W P, Liu T B, Dai J F, Wang J 2014 Acta Phys. Sin. 63 078704
[4] 苟竞, 刘俊勇, 魏震波, Gareth Taylor, 刘友波 2014 63 208402
Google Scholar
Gou J, Liu J Y, Wei Z B, Taylor G, Liu Y B 2014 Acta Phys. Sin. 63 208402
Google Scholar
[5] Pincus S M 1991 Proc. Natl. Acad. Sci. U.S.A. 88 2297
Google Scholar
[6] Richman J S, Moorman J R 2000 Am. J. Physiol. Heart Circ. Physiol. 278 H2039
Google Scholar
[7] Costa M, Goldberger A, Peng C K 2005 Phys. Rev. E 71 021906
Google Scholar
[8] 刘铁兵, 姚文坡, 宁新宝, 倪黄晶, 王俊 2013 62 218704
Google Scholar
Liu T B, Yao W P, Ning X B, Ni H J, Wang J 2013 Acta Phys. Sin. 62 218704
Google Scholar
[9] Park J H, Kim S, Kim C H, A Cichocki, Kim K 2007 Fractals 15 399
Google Scholar
[10] 杨孝敬, 杨阳, 李淮周, 钟宁 2016 65 218701
Google Scholar
Yang X J, Yang Y, Li H Z, Zhong N 2016 Acta Phys. Sin. 65 218701
Google Scholar
[11] Biswal B, Yetkin F Z, Haughton V M, Hyde J S 1995 Magn. Reson. Med. 34 537
Google Scholar
[12] Morgan V L, Abou-Khalil B, Rogers B P 2015 Brain Connect 5 35
Google Scholar
[13] Fox M D, Raichle M E 2007 Nat. Rev. Neurosci. 8 700
Google Scholar
[14] Al-Zubaidi A, Mertins A, Heldmann M, Jauch-Chara K, Münte T F 2019 Front. Hum. Neurosci. 13 00164
[15] Santos N C, Costa P C S, Cunha P, Cotter J, Sampaio A, Zihl J, Almeida O F X, Cerqueira J J, Palha J A, Sousa N 2013 Age 35 1983
Google Scholar
[16] Santos N C, Costa P S, Cunha P, Portugal-Nunes C, Amorim L, Cotter J, Cerqueira J J, Palha J A, Sousa N 2014 Front. Aging Neurosci. 6 00021
[17] Costa P S, Santos N C, Cunha P, Palha J A, Sousa N 2013 PloS one 8 e71940
Google Scholar
[18] Cabral J, Vidaurre D, Marques P, Magalhães R, Moreira P S, Soares J M, Deco G, Sousa N, Kringelbach M L 2017 Sci. Rep. 7 5135
Google Scholar
[19] Smith S M, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TEJ, Johansen-Berg H, Bannister PR, Luca MD, Drobnjak I, Flitney DE, Niazy RK, Saunders J, Vickers J, Zhang Y, Stefano ND, Brady JM, Matthews PM 2004 NeuroImage 23 S208
Google Scholar
[20] Woolrich M W, Jbabdi S, Patenaude B, Chappell M, Makni S, Behrens T, Beckmann C, Jenkinson M, Smith S M 2009 NeuroImage 45 S173
Google Scholar
[21] Jenkinson M, Beckmann C F, Behrens T E J, Woolrich M W, Smith S M 2012 NeuroImage 62 782
Google Scholar
[22] Jenkinson M, Bannister P, Brady M, Smith S 2002 NeuroImage 17 825
Google Scholar
[23] Smith S M 2002 Hum. Brain Mapp. 17 143
Google Scholar
[24] Andersson J L R, Jenkinson M, Smith S 2007 FMRIB Analysis Group of the University of Oxford 2
[25] Protzner A B, Valiante T A, Kovacevic N, McCormick C, McAndrews M P 2010 Arch. Ital. Biol. 148 289
[26] Catarino A, Churches O, Baron-Cohen S, Andrade A, Ring H 2011 Clin. Neurophysiol. 122 2375
Google Scholar
[27] Escudero J, básolo D A, Hornero R, Espino P, López M 2006 Physiol. Meas. 27 1091
Google Scholar
[28] Sokunbi M O, Fung W, Sawlani V, Choppin S, Linden D E J, Thome J 2013 Psychiat. Res. 214 341
Google Scholar
[29] Yang A C, Huang C C, Yeh H L, Liu M E, Hong C J, Tu P C, Chen J F, Huang N E, Peng C K, Lin C P, Tsai S J 2013 Neurobiol. Aging 34 428
Google Scholar
[30] Lin C, Lee S H, Huang C M, Chen G Y, Ho P S, Liu H L, Chen Y L, Lee T M C, Wu S C 2019 J. Affect. Disorders 250 270
Google Scholar
[31] Wang D J J, Jann K, Fan C, Qiao Y, Zang Y F, Lu H B, Yang Y H 2018 Front. Neurosci. 12 352
Google Scholar
[32] Niu Y, Wang B, Zhou M N, Xue J Y, Shapour H, Cao R, Cui X H, Wu J L, Xiang J 2018 Front. Neurosci. 12 00677
Google Scholar
[33] Raichle M E, MacLeod A M, Snyder A Z, Powers W J, Gusnard D A, Shulman G L 2001 Proc. Natl. Acad. Sci. U.S.A. 98 676
Google Scholar
[34] Greicius M D, Krasnow B, Reiss A L 2003 Proc. Natl. Acad. Sci. U.S.A. 100 253
Google Scholar
[35] Buckner R L, Andrews-Hanna J R, Schacter D L 2008 Ann. N. Y. Acad. Sci. 1124 1
Google Scholar
[36] Goryawala M, Zhou Q, Barker W, Loewenstein D A, Duara R, Adjouadi M 2015 Comput. Intell. Neurosci. 2015 865265
[37] Wang X N, Zeng Y, Chen G Q, Zhang Y H, Li X Y, Hao X Y, Yu Y, Zhang M, Sheng C, Li Y X 2016 Oncotarget 7 48953
[38] Smart C M, Spulber G, Garcia-Barrera M 2014 Alzheimer's Dement. 10 608
-
图 1 ELM分类器操作流程图
Figure 1. Flowchart of ELM classifier.
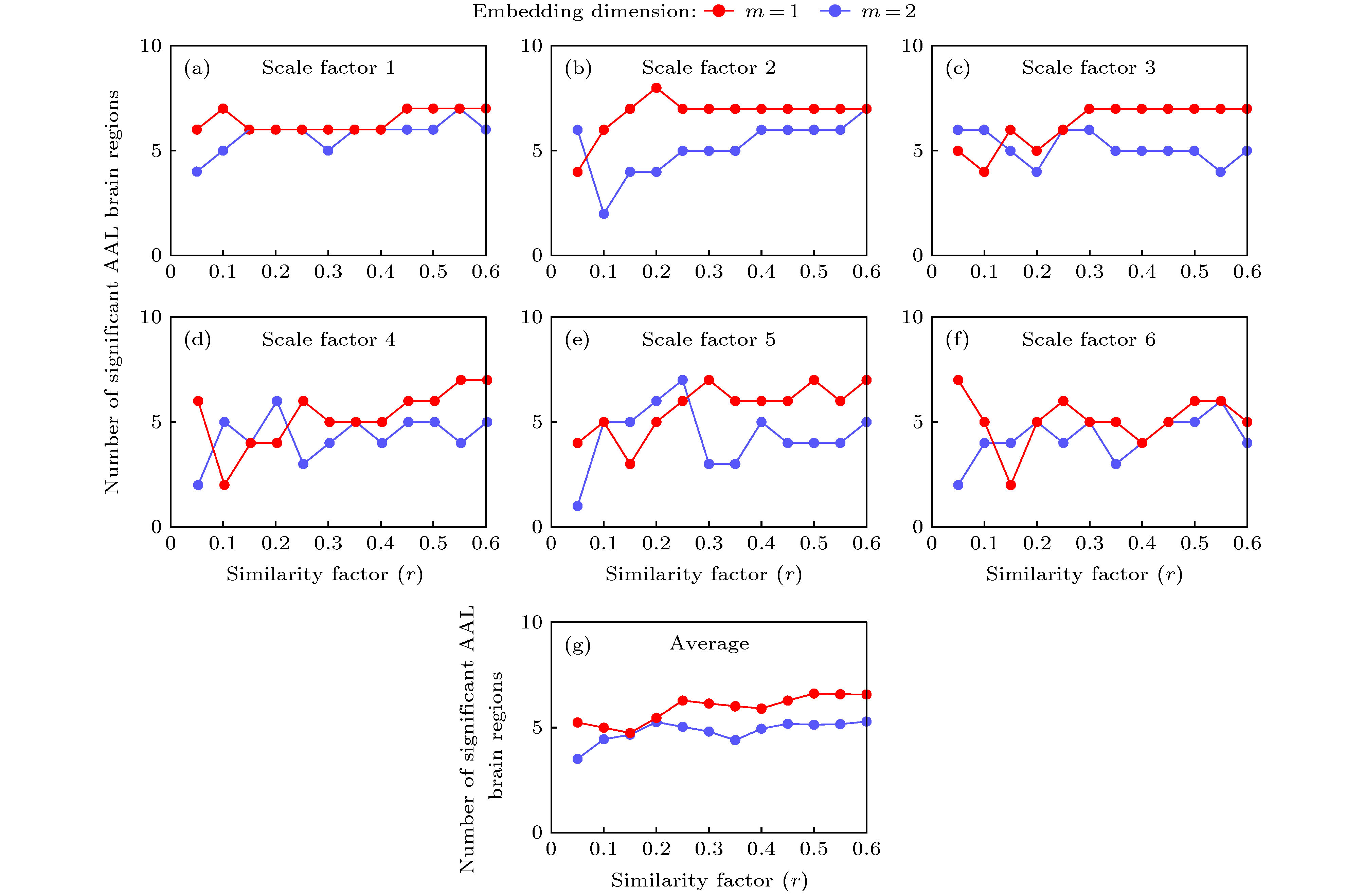
图 2 改变τ, m, r取值时, 两组样本差异较显著脑区数量 (a)—(f)在尺度因子τ分别取值1—6时, 且嵌入维数取m = 1(红色线条)和m = 2 (蓝色线条)时, 在相似系数r取0.05—0.6上分别计算所得的显著性脑区数量(p < 0.05); (g)尺度因子τ从1—6各个对应的样本熵做平均, 两组被试显著性脑区数量差异(p < 0.05)
Figure 2. The number of significant brain regions when changing scale factor τ, embedding dimension m and similar factor r in the MSE model: (a) τ = 1; (b) τ = 2; (c) τ = 3; (d) τ = 4; (e) τ = 5; (f) τ = 6; (g) average number of significant brain regions over the scale factor τ (p < 0.05). Here, the similarity factor r changed from 0.05 to 0.6 with a step of 0.05 and parameter of m = 1 (redline) was fixed and m = 2 (blueline) respectively (p < 0.05).
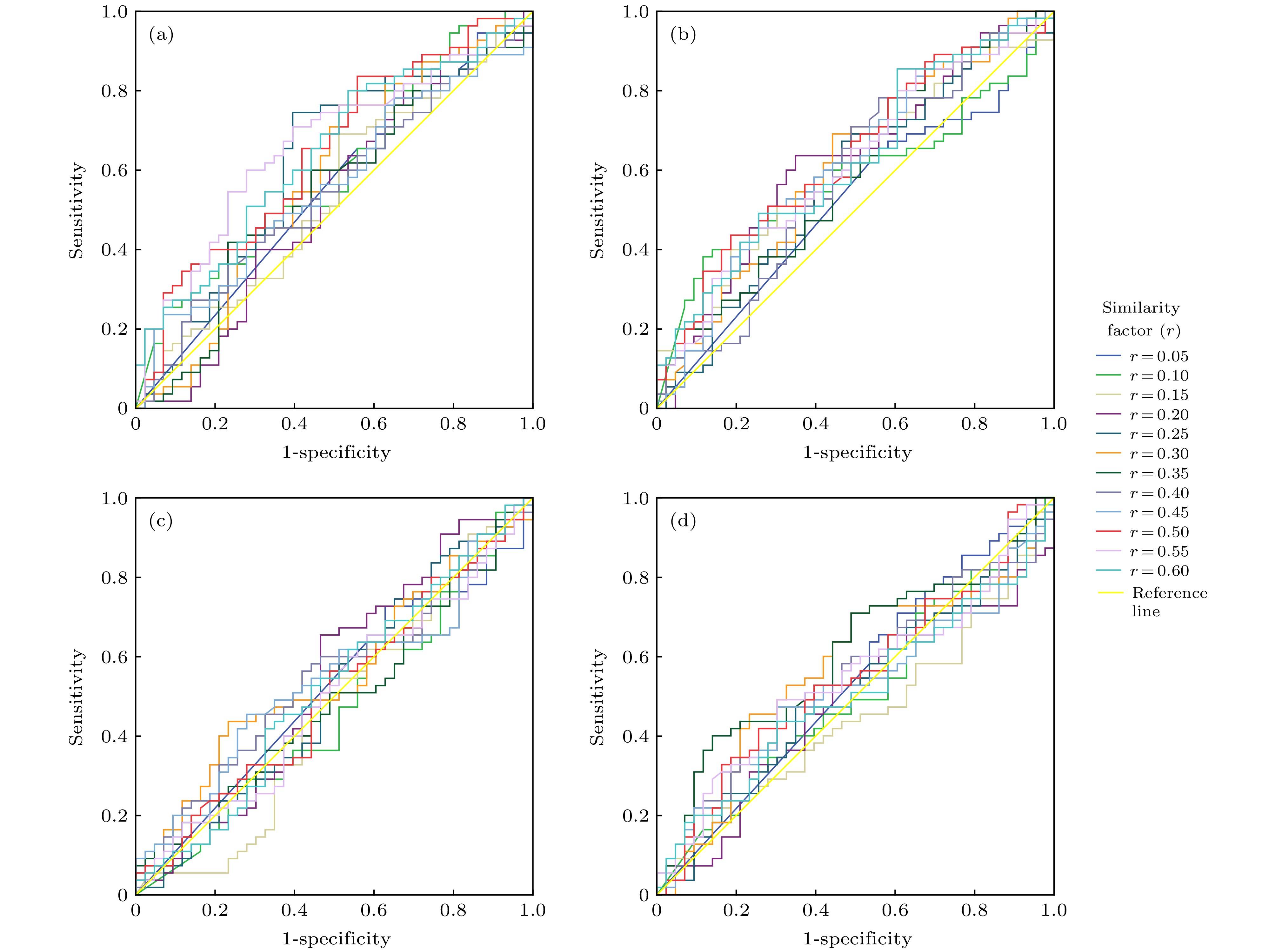
图 3 相似系数r对单个脑区分类效果的影响. 保持m = 1, τ = 5参数值不变, 调节相似系数r从0.05到0.6, 步长为0.05, 单个脑区ROC曲线和AUC值 (a)左后扣带回; (b)右颞上回; (c)右枕中回; (d)右中央后回. 图(a)和图(b)显示了对认知分数较敏感的单个标志性脑区的ROC曲线明显高于参考线的特征和较大AUC值, 可以当做本文的功能标记. 相反, 图(c)和(d)显示了对认知分数不敏感的单个非标志性脑区的ROC曲线绕于参考线周围的特征和较小AUC值
Figure 3. Sorting effects of similarity factor rby ROC and AUC value in a single brain region when the similarity factor ris setfrom 0.05 to 0.6 with a step of 0.05 and parameters of m = 1, τ = 5 fixed in the MSE model: (a) PCG.L:left posterior cingulate gyrus; (b)STG.R: right superior temporal gyrus; (c) MOG.R: right middle occipital gyrus; (d) PoCG.R: right postcentral gyrus. In above two planes such as (a) and (b), a single sensitive brain area to cognitive testing score could be characted by both ROC beyond the reference line and great AUC value, therefore, be employed as a functional biomarker in this study. In reverse, a single insensitive brain area could be characted by both ROC around the reference line and small AUC value in below two planes such as (c) and (d).
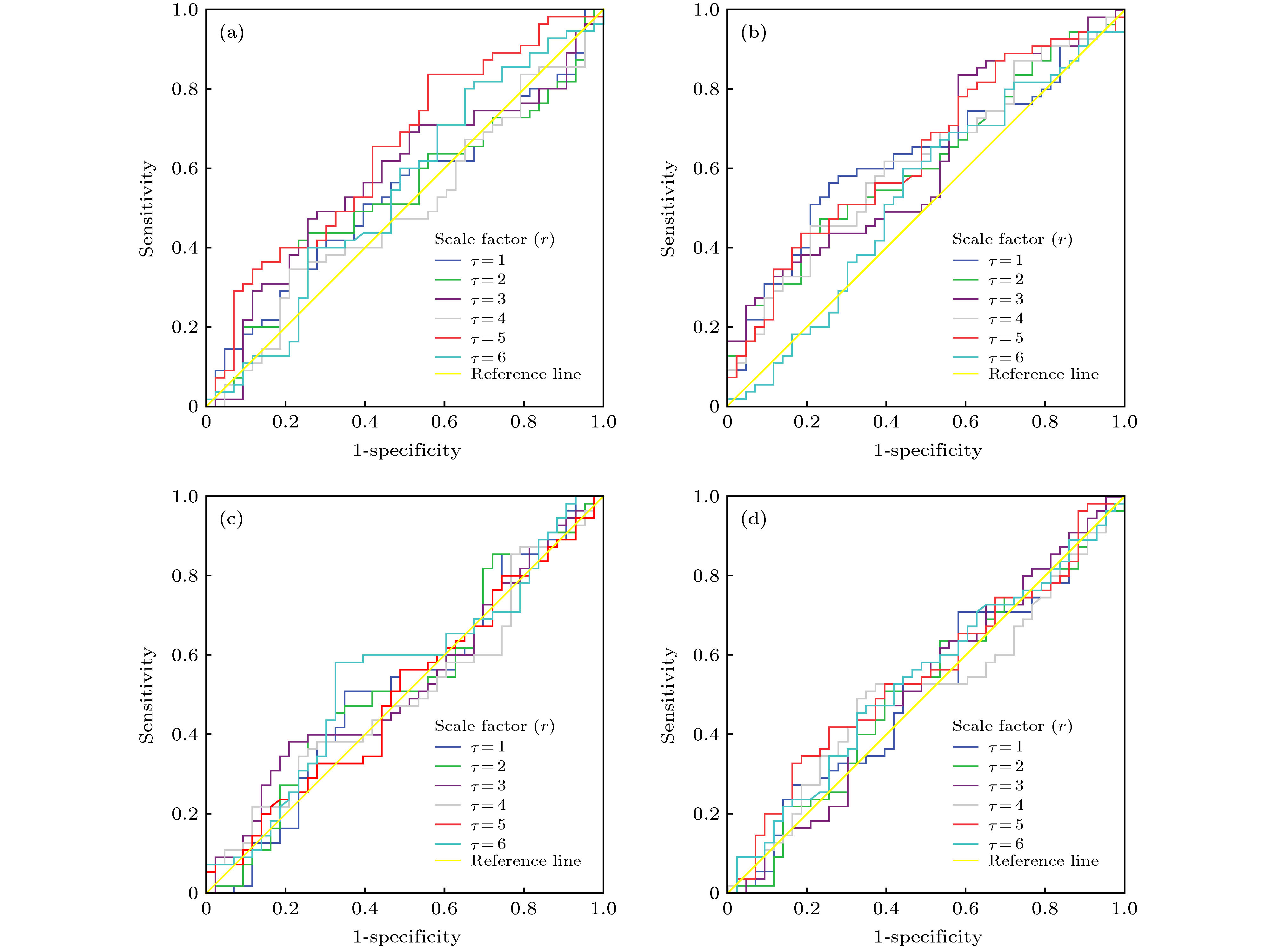
图 4 尺度因子τ对单个脑区分类效果的影响. 取优化参数m = 1和r = 0.5, 调节尺度因子τ从1到6, 步长为1, 单个脑区ROC曲线和AUC值 (a)左后扣带回; (b)右颞上回; (c)右枕中回; (d)右中央后回. 图(a)和图(b)显示了对认知分数较敏感的单个标志性脑区ROC曲线特征和较大AUC值, 可以当作本文的功能标记; 图(c)和图(d)显示了与图(a)和图(b)特征相反的单个非标志性脑区ROC曲线特征和较小AUC值
Figure 4. Sorting effects of scale factor τby ROC and AUC value in a single brain region when the scale factor τis set from 1 to 6 with a step of 1 and the optimization parameters of m = 1 and r =0.5 fixed in the MSE model: (a) PCG.L: left posterior cingulate gyrus; (b) STG.R: right superior temporal gyrus; (c) MOG.R: rightmiddle occipital gyrus; (d) PoCG.R: rightpostcentral gyrus.In above two planes such as (a) and (b), a single sensitive brain area to the cognitive testing score could be characted by both ROC beyond the reference line and great AUC value, therefore, be employed as a functional biomaker in this study. In reverse, a single insensitive brain area to the cognitive testing score could be characted by both ROC around the reference line and small AUC value in below two planes such as (c) and (d).
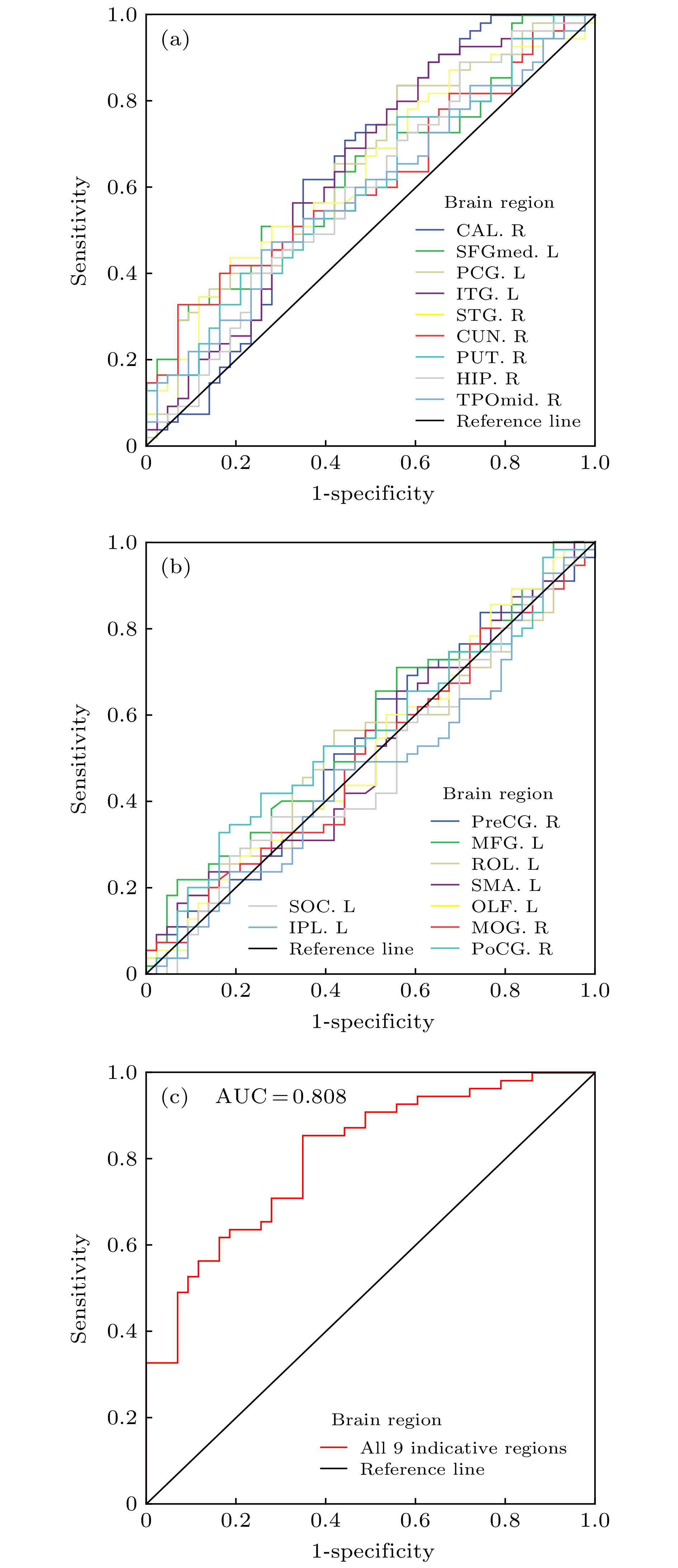
图 5 在优化参数下(即m = 1, r = 0.5和τ = 5)单个标志性脑区、单个非标志性脑区以及9个全部标志性脑区参与的ROC和AUC值 (a)单个标志性脑区. 共9个; (b)单个非标志性脑区. 随机选取9个; (c)全部9个标志性脑区同时参与
Figure 5. Respective ROC and AUC value of a single indicative brain region, a single non-indicative brain regions and a total of 9 indicative brain regions at the optimization parameters of m = 1, r = 0.5 and τ = 5 in the MSE model: (a) A single indicative brain region. A total of 9 indicative brain regions. (b)a single of non-indicative brain region. A total of 9 non-indicative brain regions are randomly chosen; (c) a total of 9 indicative brain regions all together.
图 6 尺度因子τ取1—5时全部9个标志性脑区的组间MSE变化规律 (a)右距状裂周围皮层; (b)左内侧额上回; (c)左后扣带回; (d)左颞下回; (e)右颞上回; (f)右楔叶; (g)右豆状壳核; (h)右海马; (i)右颞极: 颞中回. (组间差异显著性: *表示p < 0.05)
Figure 6. Inter-group MSE values change with the parameter of scale factor τ (from 1 to 5 with a step of 1) in a total of 9 indicative brain regions: (a) CAL.R; (b) SFGmed.L; (c) PCG.L; (d) ITG.L; (e) STG.R; (f) CUN.R; (g) PUT.R; (h) HIP.R; (i)TPOmid.R. (*p < 0.05).
图 7 ELM测试分类准确率. 通过在训练集和测试集上运行ELM进行分类, 对认知分数优(类别1)与差(类别0)的两组样本实现约为80%分类准确率
Figure 7. Classification accuracy tested by ELM. Two groups of samples with excellent cognitive scores (Category 1) and poor cognitive scores (Category 0) could be classified at a sorting rate of about 80%.
表 1 AUC值表达的相似系数r对单个脑区分类效果的影响
Table 1. Effect of similarity factor r on sorting rate by the AUC value of each single brain region.
Similarity factor (r) PCG.L STG.R MOG.R PoCG.R r = 0.05 0.557 0.518 0.512 0.535 r = 0.10 0.597 0.578 0.463 0.502 r = 0.15 0.541 0.613 0.459 0.450 r = 0.20 0.523 0.619 0.542 0.479 r = 0.25 0.612 0.578 0.510 0.515 r = 0.30 0.580 0.616 0.550 0.567 r = 0.35 0.552 0.588 0.492 0.603 r = 0.30 0.548 0.582 0.543 0.544 r = 0.45 0.561 0.621 0.542 0.519 r = 0.50 0.644 0.638 0.507 0.550 r = 0.55 0.665 0.616 0.499 0.547 r = 0.60 0.641 0.624 0.519 0.507 
DownLoad: CSV
表 2 AUC值表达的尺度因子τ对单个脑区分类效果的影响
Table 2. Effect of scale factor τ on sorting rate by the AUC value of each single brain region.
Scale factor (τ) PCG.L STG.R MOG.R PoCG.R τ = 1 0.532 0.628 0.522 0.508 τ = 2 0.526 0.614 0.531 0.510 τ = 3 0.573 0.620 0.529 0.521 τ = 4 0.494 0.617 0.506 0.512 τ = 5 0.644 0.638 0.507 0.550 τ = 6 0.542 0.534 0.551 0.539
DownLoad: CSV
表 3 几种不同相似系数r时所构建特征向量的组间显著性差异
Table 3. Inter-group difference significance of eigenvectors at similarity factors(r).
Similarity
factor (r)Significance
(p-value)Similarity
factor (r)Significance
(p-value)0.15 0.6220 0.25 0.0358 0.35 0.0160 0.45 0.0027 0.50 < 0.001
DownLoad: CSV
表 4 几种不同尺度因子τ时所构建特征向量的组间显著性差异
Table 4. Inter-group difference significance of eigenvectors at the scale factor(τ).
Scale
factor (τ)Significance
(p-value)Scale
factor (τ)Significance
(p-value)1 0.0559 2 0.0328 3 0.0069 4 0.0101 5 < 0.001
DownLoad: CSV
表 5 经10折交叉验证得到的分类精度
Table 5. Classification rate (CR) tested by 10-fold cross validation.
N CR N CR N CR 1 0.6325 6 1.0000 Average 0.8013 2 1.0000 7 0.7906 3 0.9000 8 0.6838 4 0.6325 9 0.6838 5 1.0000 10 0.6895
DownLoad: CSV
-
[1] Costa M, Goldberger A, Peng C K 2002 Phys. Rev. Lett. 89 068102
Google Scholar
[2] Rosso O A, Martin M T, PlastinoA 2002 Phys. A 313 587
Google Scholar
[3] 姚文坡, 刘铁兵, 戴加飞, 王俊 2014 63 078704
Yao W P, Liu T B, Dai J F, Wang J 2014 Acta Phys. Sin. 63 078704
[4] 苟竞, 刘俊勇, 魏震波, Gareth Taylor, 刘友波 2014 63 208402
Google Scholar
Gou J, Liu J Y, Wei Z B, Taylor G, Liu Y B 2014 Acta Phys. Sin. 63 208402
Google Scholar
[5] Pincus S M 1991 Proc. Natl. Acad. Sci. U.S.A. 88 2297
Google Scholar
[6] Richman J S, Moorman J R 2000 Am. J. Physiol. Heart Circ. Physiol. 278 H2039
Google Scholar
[7] Costa M, Goldberger A, Peng C K 2005 Phys. Rev. E 71 021906
Google Scholar
[8] 刘铁兵, 姚文坡, 宁新宝, 倪黄晶, 王俊 2013 62 218704
Google Scholar
Liu T B, Yao W P, Ning X B, Ni H J, Wang J 2013 Acta Phys. Sin. 62 218704
Google Scholar
[9] Park J H, Kim S, Kim C H, A Cichocki, Kim K 2007 Fractals 15 399
Google Scholar
[10] 杨孝敬, 杨阳, 李淮周, 钟宁 2016 65 218701
Google Scholar
Yang X J, Yang Y, Li H Z, Zhong N 2016 Acta Phys. Sin. 65 218701
Google Scholar
[11] Biswal B, Yetkin F Z, Haughton V M, Hyde J S 1995 Magn. Reson. Med. 34 537
Google Scholar
[12] Morgan V L, Abou-Khalil B, Rogers B P 2015 Brain Connect 5 35
Google Scholar
[13] Fox M D, Raichle M E 2007 Nat. Rev. Neurosci. 8 700
Google Scholar
[14] Al-Zubaidi A, Mertins A, Heldmann M, Jauch-Chara K, Münte T F 2019 Front. Hum. Neurosci. 13 00164
[15] Santos N C, Costa P C S, Cunha P, Cotter J, Sampaio A, Zihl J, Almeida O F X, Cerqueira J J, Palha J A, Sousa N 2013 Age 35 1983
Google Scholar
[16] Santos N C, Costa P S, Cunha P, Portugal-Nunes C, Amorim L, Cotter J, Cerqueira J J, Palha J A, Sousa N 2014 Front. Aging Neurosci. 6 00021
[17] Costa P S, Santos N C, Cunha P, Palha J A, Sousa N 2013 PloS one 8 e71940
Google Scholar
[18] Cabral J, Vidaurre D, Marques P, Magalhães R, Moreira P S, Soares J M, Deco G, Sousa N, Kringelbach M L 2017 Sci. Rep. 7 5135
Google Scholar
[19] Smith S M, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TEJ, Johansen-Berg H, Bannister PR, Luca MD, Drobnjak I, Flitney DE, Niazy RK, Saunders J, Vickers J, Zhang Y, Stefano ND, Brady JM, Matthews PM 2004 NeuroImage 23 S208
Google Scholar
[20] Woolrich M W, Jbabdi S, Patenaude B, Chappell M, Makni S, Behrens T, Beckmann C, Jenkinson M, Smith S M 2009 NeuroImage 45 S173
Google Scholar
[21] Jenkinson M, Beckmann C F, Behrens T E J, Woolrich M W, Smith S M 2012 NeuroImage 62 782
Google Scholar
[22] Jenkinson M, Bannister P, Brady M, Smith S 2002 NeuroImage 17 825
Google Scholar
[23] Smith S M 2002 Hum. Brain Mapp. 17 143
Google Scholar
[24] Andersson J L R, Jenkinson M, Smith S 2007 FMRIB Analysis Group of the University of Oxford 2
[25] Protzner A B, Valiante T A, Kovacevic N, McCormick C, McAndrews M P 2010 Arch. Ital. Biol. 148 289
[26] Catarino A, Churches O, Baron-Cohen S, Andrade A, Ring H 2011 Clin. Neurophysiol. 122 2375
Google Scholar
[27] Escudero J, básolo D A, Hornero R, Espino P, López M 2006 Physiol. Meas. 27 1091
Google Scholar
[28] Sokunbi M O, Fung W, Sawlani V, Choppin S, Linden D E J, Thome J 2013 Psychiat. Res. 214 341
Google Scholar
[29] Yang A C, Huang C C, Yeh H L, Liu M E, Hong C J, Tu P C, Chen J F, Huang N E, Peng C K, Lin C P, Tsai S J 2013 Neurobiol. Aging 34 428
Google Scholar
[30] Lin C, Lee S H, Huang C M, Chen G Y, Ho P S, Liu H L, Chen Y L, Lee T M C, Wu S C 2019 J. Affect. Disorders 250 270
Google Scholar
[31] Wang D J J, Jann K, Fan C, Qiao Y, Zang Y F, Lu H B, Yang Y H 2018 Front. Neurosci. 12 352
Google Scholar
[32] Niu Y, Wang B, Zhou M N, Xue J Y, Shapour H, Cao R, Cui X H, Wu J L, Xiang J 2018 Front. Neurosci. 12 00677
Google Scholar
[33] Raichle M E, MacLeod A M, Snyder A Z, Powers W J, Gusnard D A, Shulman G L 2001 Proc. Natl. Acad. Sci. U.S.A. 98 676
Google Scholar
[34] Greicius M D, Krasnow B, Reiss A L 2003 Proc. Natl. Acad. Sci. U.S.A. 100 253
Google Scholar
[35] Buckner R L, Andrews-Hanna J R, Schacter D L 2008 Ann. N. Y. Acad. Sci. 1124 1
Google Scholar
[36] Goryawala M, Zhou Q, Barker W, Loewenstein D A, Duara R, Adjouadi M 2015 Comput. Intell. Neurosci. 2015 865265
[37] Wang X N, Zeng Y, Chen G Q, Zhang Y H, Li X Y, Hao X Y, Yu Y, Zhang M, Sheng C, Li Y X 2016 Oncotarget 7 48953
[38] Smart C M, Spulber G, Garcia-Barrera M 2014 Alzheimer's Dement. 10 608
DownLoad:
Catalog
Metrics
- Abstract views: 7270
- PDF Downloads: 74
- Cited By: 0
