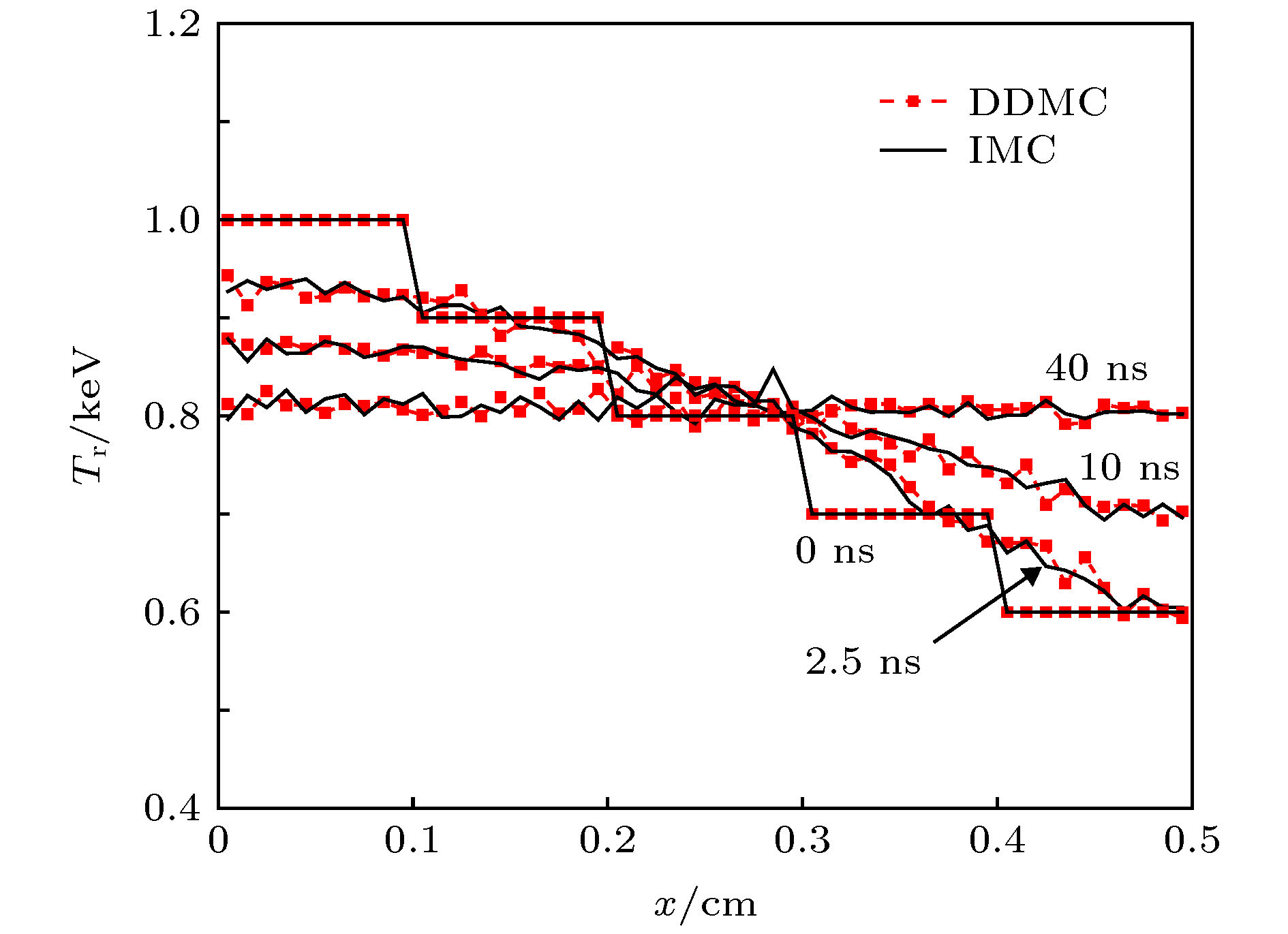
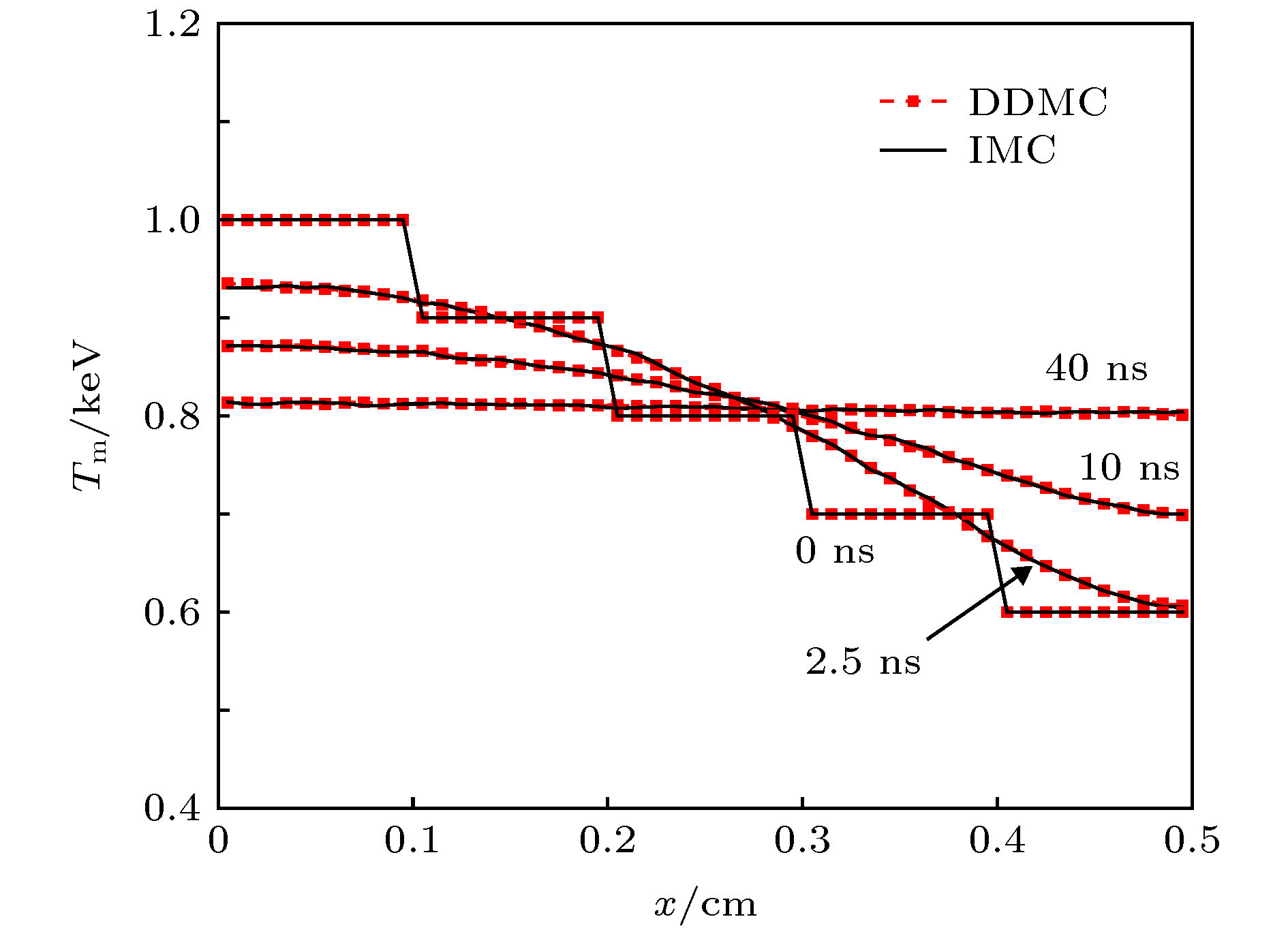
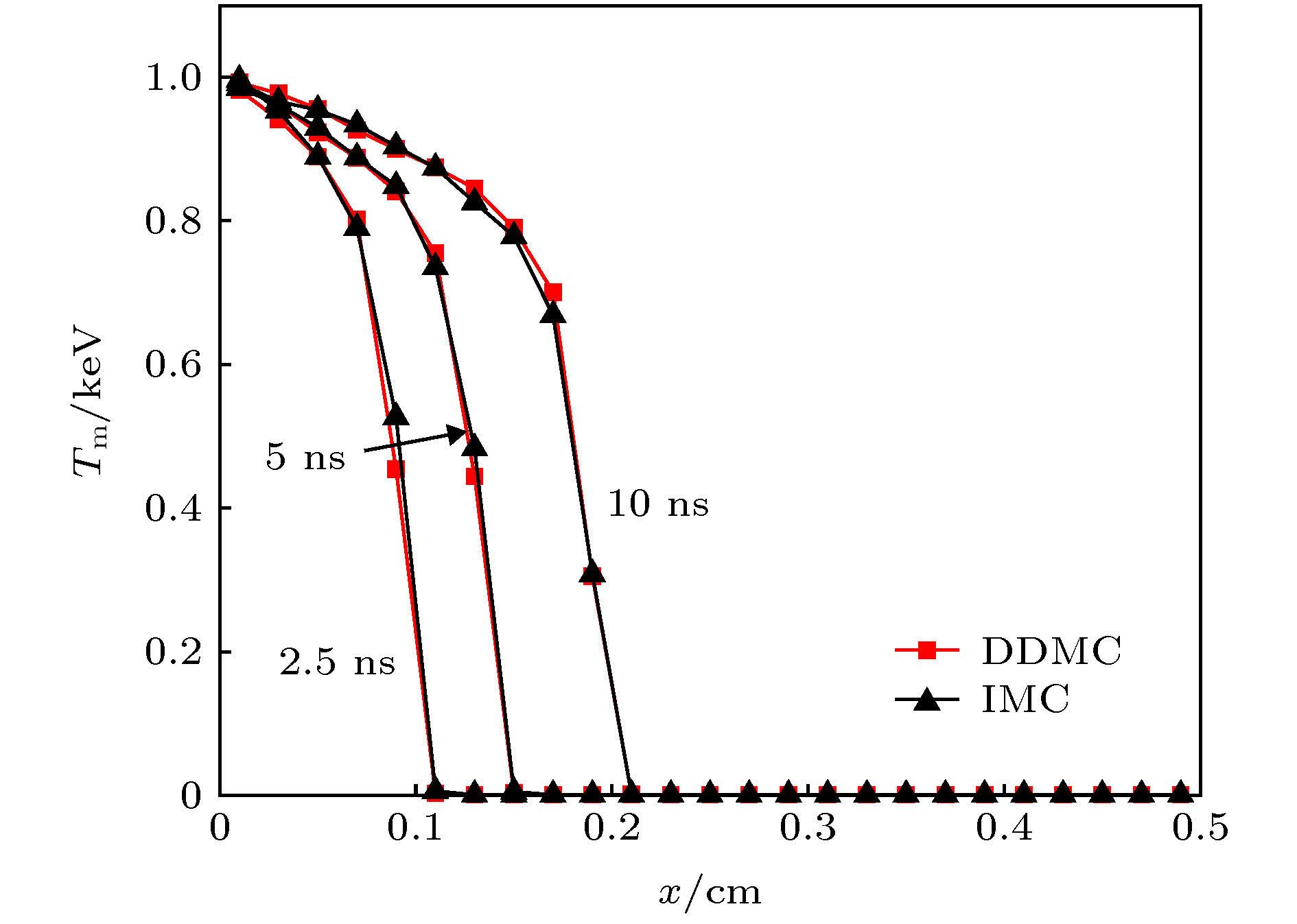
-
Thermal radiation transfer in material and the interaction between radiative photon and material are important research projects of the inertial confinement fusion, and Monte Carlo method is one of the important researching methods. Based on the implicit integral-differential transport equation, traditional implicit Monte Carlo method can accurately simulate the thermal radiation transport in material. However, the implicit Monte Carlo method would take quite a long computational time when the opacity is increased because scattering events are dominant in particles’ histories, thus reducing the simulation efficiency. In this paper, based on discrete diffusion Monte Carlo method, i.e. a radiation transport code, the discrete diffusion Monte Carlo radiation transport simulation, is developed. The code increases the efficiency of thermal radiation simulations in a high opacity range, but it can yield insufficiently accurate results in a low opacity range. There exist low opacity material and high opacity material in the inertial confinement fusion. In this work, investigated are several numerical techniques that can improve the utility and accuracy of discrete diffusion Monte Carlo for grey thermal radiation simulation. First, the discrete diffusion Monte Carlo method and implicit Monte Carlo method are combined. Second, a new method of treating the interface between the diffusive region and the transport region is proposed. Finally, a hybrid radiative transfer program is developed. In order to verify the hybrid radiative transfer program and the new interface method, a series of numerical experiments for typical thermal radiation transport problem is conducted. In these problems, materials with different opacities are tested. Then the simulation efficiencies and curves of temperature, obtained by the two Monte Carlo methods, are analyzed. According to the simulation results, the program can not only accurately simulate the radiation transport in material with high opacity, but also remarkably increase the simulation efficiency. This is because many implicit Monte Carlo steps are substituted by one diffusive step and the details in the diffusive step are ignored. Also, the propagation of thermal radiation depicted with figures and tables are consistent with the radiation transport theory. In addition, the results from the hybrid Monte Carlo method reach the same accuracy as that from the implicit Monte Carlo method, and the simulation efficiency is remarkably increased.
-
Keywords:
- thermal radiation transport /
- implicit Monte Carlo method /
- discrete diffusion Monte Carlo method /
- interface methods
[1] 彭惠民 2008 等离子体中辐射输运和辐射流体力学 (北京: 国防工业出版社) 第38页
Peng H M 2008 Radiation Transport and Radiation Hydrodynamics in Plasmas (Beijing: National Defense Industry Press) p38 (in Chinese)
[2] Hammersly J M, Handscomb D C 1964 Monte Carlo Method (New York: John Wiley & Sons Press) p76
[3] 裴鹿成, 张孝泽 1980 蒙特卡罗方法及其在粒子输运问题中的应用(北京: 科学出版社) 第18页
Pei L C, Zhang X Z 1980 Monte Carlo Method and Application in Particle Transportation (Beijing: Science Press) p18 (in Chinese)
[4] Fleck J A 1963 Computational Method in the Physical Sciences (New York: McGraw-Hill) p43
[5] Campbell P M, Nelson R G 1964 Livermore, Calif: Lawrence Radiation Laboratory Report UCRL-7838
[6] Fleck J A, Cummings J D 1971 J. Comput. Phys. 8 313
Google Scholar
[7] Fleck J A, Canfield E H 1984 J. Comput. Phys. 54 508
Google Scholar
[8] Giorla J, Sentis R 1987 J. Comput. Phys. 70 145
Google Scholar
[9] Urbatsch T J, Morel J E, Gulick J C 1999 Proceedings of the ANS conference on Mathematics and Computation, Reactor Physics, and Environmental Analysis in Nuclear Applications Madrid, Spain, September 27–30, 1999 p262
[10] Evans T M, Urbatsch T J, Lichtenstein H 2000 Proceedings of the Monte Carlo 2000 International Conference Lisbon, Portugal, October 23–26, 2000
[11] Gentile N A 2001 J. Comput. Phys. 172 543
Google Scholar
[12] Densmore J D, Urbatsch T J, Evans T M, Buksas M W 2005 American Nuclear Society Topical Meeting in Mathematics and Computations Avignon, France, September 12–15, 2005
[13] Densmore J D, Urbatsch T J, Evans T M, Buksas M W 2007 J. Comput. Phys. 222 485
Google Scholar
[14] Cleveland M A, Gentile N, Palmer T S 2010 J. Comput. Phys. 229 5707
Google Scholar
[15] Densmore J D, Thompson K G, Urbatsch T J 2012 J. Comput. Phys. 231 6924
Google Scholar
[16] 李树, 李刚, 田东风, 邓力 2013 62 249501
Google Scholar
Li S, Li G, Tian D F, Deng L 2013 Acta Phys. Sin. 62 249501
Google Scholar
[17] 李树, 陈耀华, 姬志成, 章明宇, 任国利, 霍文义, 闫威华, 韩小英, 李志超, 刘杰, 蓝可 2018 67 025202
Google Scholar
Li S, Chen Y H, Ji Z C, Zhang M Y, Ren G L, Huo W Y, Yan W H, Han X Y, Li Z C, Liu J, Lan K 2018 Acta Phys. Sin. 67 025202
Google Scholar
[18] Mihalas D, Mihalas B W, Fu A, Arnett W D 1986 Phys. Today 39 90
Google Scholar
[19] 谢仲生 2004 核反应堆物理分析 (西安: 西安交通大学出版社) 第62页
Xie Z S 2004 Analysis of Nuclear Reactor Physics (Xi’an: Xi’an Jiaotong University Press) p62 (in Chinese)
[20] Szilard R H, Pomraning G C 1992 Nucl. Sci. Eng. 112 256
Google Scholar
[21] Habetle G J, Matkowsky B J 1975 J. Math. Phys. 16 846
Google Scholar
[22] Densmore J D, Davidson G, Carrington D B 2006 Ann. Nucl. Energy 33 583
Google Scholar
[23] Cashwell E D, Everett C J 1959 A Practical Manual on the Monte Carlo Method for Random Walk Problem (London: Pergamon Press) p19
-
图 1 不同时刻的物质温度空间分布比较(σ0 = 500)
Figure 1. Material temperature in different moments (σ0 = 500).
图 2 不同时刻的辐射温度空间分布比较(σ0 = 500)
Figure 2. Radiative temperature in different moments (σ0 = 500).
图 3 不同时刻的物质温度空间分布比较(σ0 = 500)
Figure 3. Material temperature in different moments (σ0 = 500).
图 4 不同时刻的辐射温度空间分布比较(σ0 = 500)
Figure 4. Radiative temperature in different moments (σ0 = 500).
图 5 不同时刻的物质温度空间分布比较(σ0 = 500, Np = 500000)
Figure 5. Material temperature in different moments (σ0 = 500, Np = 500000).
图 6 不同时刻的辐射温度空间分布比较(σ0 = 500, Np = 500000)
Figure 6. Radiative temperature in different moments (σ0 = 500, Np = 500000).
图 7 不同时刻介质中物质温度的空间分布比较
Figure 7. Material temperature in different moments.
表 1 不同σ0取值下IMC与DDMC方法的模拟时间对比
Table 1. Simulation time of IMC method and DDMC method in different initial cross sections.
σ0/keV3·cm–1 IMC time/s DDMC time/s Speed up 200 330.4 143.3 2.3 500 505.8 139.9 3.6 1000 894.2 142.1 6.3 2000 1158.6 142.2 8.1 
DownLoad: CSV
表 2 不同σ0取值下, IMC与DDMC方法的模拟时间比较
Table 2. Simulation time of IMC method and DDMC method in different initial cross sections.
σ0/keV3·cm–1 IMC time/s DDMC time/s Speed up 200 1184.4 298.2 4.0 500 2357.6 291.8 8.1 1000 4348.7 288.6 15.1 2000 8406.4 287.7 29.2
DownLoad: CSV
-
[1] 彭惠民 2008 等离子体中辐射输运和辐射流体力学 (北京: 国防工业出版社) 第38页
Peng H M 2008 Radiation Transport and Radiation Hydrodynamics in Plasmas (Beijing: National Defense Industry Press) p38 (in Chinese)
[2] Hammersly J M, Handscomb D C 1964 Monte Carlo Method (New York: John Wiley & Sons Press) p76
[3] 裴鹿成, 张孝泽 1980 蒙特卡罗方法及其在粒子输运问题中的应用(北京: 科学出版社) 第18页
Pei L C, Zhang X Z 1980 Monte Carlo Method and Application in Particle Transportation (Beijing: Science Press) p18 (in Chinese)
[4] Fleck J A 1963 Computational Method in the Physical Sciences (New York: McGraw-Hill) p43
[5] Campbell P M, Nelson R G 1964 Livermore, Calif: Lawrence Radiation Laboratory Report UCRL-7838
[6] Fleck J A, Cummings J D 1971 J. Comput. Phys. 8 313
Google Scholar
[7] Fleck J A, Canfield E H 1984 J. Comput. Phys. 54 508
Google Scholar
[8] Giorla J, Sentis R 1987 J. Comput. Phys. 70 145
Google Scholar
[9] Urbatsch T J, Morel J E, Gulick J C 1999 Proceedings of the ANS conference on Mathematics and Computation, Reactor Physics, and Environmental Analysis in Nuclear Applications Madrid, Spain, September 27–30, 1999 p262
[10] Evans T M, Urbatsch T J, Lichtenstein H 2000 Proceedings of the Monte Carlo 2000 International Conference Lisbon, Portugal, October 23–26, 2000
[11] Gentile N A 2001 J. Comput. Phys. 172 543
Google Scholar
[12] Densmore J D, Urbatsch T J, Evans T M, Buksas M W 2005 American Nuclear Society Topical Meeting in Mathematics and Computations Avignon, France, September 12–15, 2005
[13] Densmore J D, Urbatsch T J, Evans T M, Buksas M W 2007 J. Comput. Phys. 222 485
Google Scholar
[14] Cleveland M A, Gentile N, Palmer T S 2010 J. Comput. Phys. 229 5707
Google Scholar
[15] Densmore J D, Thompson K G, Urbatsch T J 2012 J. Comput. Phys. 231 6924
Google Scholar
[16] 李树, 李刚, 田东风, 邓力 2013 62 249501
Google Scholar
Li S, Li G, Tian D F, Deng L 2013 Acta Phys. Sin. 62 249501
Google Scholar
[17] 李树, 陈耀华, 姬志成, 章明宇, 任国利, 霍文义, 闫威华, 韩小英, 李志超, 刘杰, 蓝可 2018 67 025202
Google Scholar
Li S, Chen Y H, Ji Z C, Zhang M Y, Ren G L, Huo W Y, Yan W H, Han X Y, Li Z C, Liu J, Lan K 2018 Acta Phys. Sin. 67 025202
Google Scholar
[18] Mihalas D, Mihalas B W, Fu A, Arnett W D 1986 Phys. Today 39 90
Google Scholar
[19] 谢仲生 2004 核反应堆物理分析 (西安: 西安交通大学出版社) 第62页
Xie Z S 2004 Analysis of Nuclear Reactor Physics (Xi’an: Xi’an Jiaotong University Press) p62 (in Chinese)
[20] Szilard R H, Pomraning G C 1992 Nucl. Sci. Eng. 112 256
Google Scholar
[21] Habetle G J, Matkowsky B J 1975 J. Math. Phys. 16 846
Google Scholar
[22] Densmore J D, Davidson G, Carrington D B 2006 Ann. Nucl. Energy 33 583
Google Scholar
[23] Cashwell E D, Everett C J 1959 A Practical Manual on the Monte Carlo Method for Random Walk Problem (London: Pergamon Press) p19
DownLoad:
Catalog
Metrics
- Abstract views: 9185
- PDF Downloads: 132
- Cited By: 0
